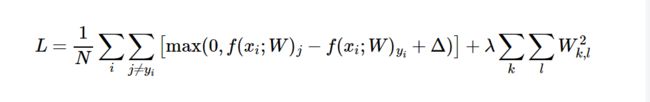机器学习之从基础数学深入剖析逻辑回归（案例理论相结合）

逻辑回归

一、从回归问题到分类问题

回归基础请见上一篇文章：https://blog.csdn.net/sjjsaaaa/article/details/115967347

1.机器学习中的分类问题

事物的类别，正确的分类观是建立科学体系、训练逻辑思维能力的重要一步。
举例：

• 根据客户的收入、存款、性别、年龄以及流水，为客户的信用等级分类。
• 读入图片，为图片内容分类（猫、狗、虎、兔）
• 手写数字识别，输出类别0-9
• 手写文字识别。也是分类问题，只是输出类别有很多，有成千上万个类。

而机器学习的分类方法，也是要找到一个合适的函数，拟合输入和输出的关系，输入一个或一系列事物的特征，输出这个事物的类别。

所有的特征里，都要转换成数值形式，才易于被机器学习，机器不能识别“男”，“女”，只能识别1，2.这种文本到数值的转换是必做的特征工程。

逻辑回归的一个算法细节，在输出明确的离散分类值之前，算法首先输出的其实是一个可能性，可以理解成概率：

• 机器学习模型根据输入数据判断一个人患心脏病的可能性为80%，那么就把这个人判定为“患病：类，输出数值1.
• 机器学习模型根据输入数据判断一个人患心脏病的可能性为30%，那么就把这个人判定为“健康：类，输出数值0.

机器学习的分类过程，也就是判定某一事物隶属于某一个类别的可能性大小的过程。

2.用线性回归+阶跃函数完成分类

如下图：横坐标为分数：0-100，纵坐标只有两个结果，要么通过考试（y=1），要么挂科(y=0)。


我们画出两种回归线的方式，去分类，明显一看，第一种图的平均误差就比较小，所以损失就少，第二种图的平均误差较大，损失也是比较大的，而函数的目标就是减少损失。

那么怎么把这条先行会u给i的函数线转成逻辑分类呢，就要用到逻辑函数。

我们注意到在60分的时候，考试的通过率为50%，而线性回归函数做假设函数时，所对应的y值正好是0.5。

阶跃函数
只要将线性回归的结果做一个简单的转换，就可以得到分类器的结果，如图：

这可以分为以下两种情况：

• 线性回归模型输出的结果大于0.5，分类输入1。
• 线性回归模型输出的结果小于0.5，分类输入0。

这就是阶跃函数，首先利用线性回归的模型，找到了概率为0.5时所对应的特征点（分数60），然后把线性的连续值，转换成0/1的分类值，取更好的拟合数据。

但是！！！！！
当有同学的成绩为0分时该怎么办，本来样本数量就不多，一个离群的样本会造成线性回归模型发生改变，这会影响模型的准确性。（见下面）

3.通过Sigmiod函数进行转换

如果有一种S形的函数，不管有多少同学考0分都不会对这个函数的形状产生大的影响，因为这个函数对于靠近0和100附近的极端样本时很不敏感的。

所以！！！！！！！！ 这个函数就是Sigmiod：

这种S形的函数，被称为logistic function，翻译为逻辑函数，在机器学习中被广泛应用与逻辑回归分类和神经网络激活过程

公式为：

这里的z是一个中间变量，代表的是线性回归的结果。
代码实现y_hat = 1/(1+np.exp(-z))。
通过Sigmoid函数就能够比阶跃函数更好地把线性函数求出的数值，转成一个0~1的分类概率值。

4.逻辑回归的假设函数

建立机器学习的模型，重点要确定假设函数h(x),来预测y’

步骤：

1. 首先通过线性回归的模型求出一个中间值z,z=w0x0+w1x1+……+wnxn+b = W^TX。它是一个连续值，区间并不在【0，1】之间，可能小于0或大于1，范围从无穷小到无穷大。
2. 然后通过逻辑函数把这个中间值z转化为0~1的概率值，以提高拟合效果。

3. 结合步骤1和2，把新的函数表示为假设函数的形式：
这个值就是逻辑回归算法得到的y’
4. 最后还要根据y‘所代表的概率，确定分类结果
如果h(x)>0.5，分类结果为1
如果h(x)<0.5,分类结果为0.

综上所述，逻辑回归所作的事情，就是把线性回归输出任意值，通过数学上的转换，输出为0-1的结果，以体现二元分类的概率

Sigmoid函数的优点：

• 是连续函数，具有单调递增性。
• 具有可微性，可以进行微分，也可以进行求导。
• 输出范围[0,1]，结果可以表示为概率的形式，为分类输出做准备。
• 抑制分类的两边，对中间区域的细微变化敏感，这对分类结果拟合效果好。

5.逻辑回归的损失函数

下一步就是确定函数参数的过程，也同样是通过计算假设函数带来的损失，找到最优的w和b的过程，也就是把误差最小化。

把训练集中所有的预测所得概率和实际结果的差异求和，并取平均值，就可以得到平均误差，这就是逻辑回归的损失函数：

然而在逻辑回归中，不能使用MSE，因为经过了一个逻辑函数的转换之后，MSE对于w和b而言，不再是一个凸函数，这样的话，就无法通过梯度下降找到全局最低点。

然而此时为了陷入局部最低点，我们为逻辑回归选择了符合条件的新的损失函数：

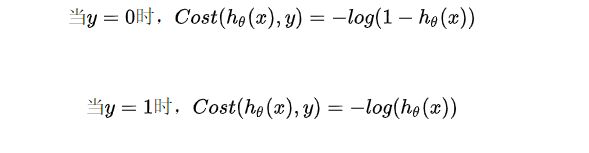
6.逻辑回归的梯度下降

逻辑回归的梯度下降过程和线性回归一样，先是进行微分，然后把计算出来的导数乘以一个学习效率α，通过不断的迭代，更新w和b，直至收敛。

引入学习速率之后，参数随梯度变化而更新的公式如下：

下面的代码实现了一个完整的逻辑回归的梯度下降过程：

# 然后构建梯度下降的函数
def gradient_descent(X,y,w,b,lr,iter) : #定义逻辑回归梯度下降函数
    l_history = np.zeros(iter) # 初始化记录梯度下降过程中误差值(损失)的数组
    w_history = np.zeros((iter,w.shape[0],w.shape[1])) # 初始化权重记录的数组
    b_history = np.zeros(iter) # 初始化记录梯度下降过程中偏置的数组  
    for i in range(iter): #进行机器训练的迭代
        y_hat = sigmoid(np.dot(X,w) + b) #Sigmoid逻辑函数+线性函数(wX+b)得到y'
        loss = -(y*np.log(y_hat) + (1-y)*np.log(1-y_hat)) # 计算损失
        derivative_w = np.dot(X.T,((y_hat-y)))/X.shape[0]  # 给权重向量求导
        derivative_b = np.sum(y_hat-y)/X.shape[0] # 给偏置求导
        w = w - lr * derivative_w # 更新权重向量，lr即学习速率alpha
        b = b - lr * derivative_b   # 更新偏置，lr即学习速率alpha
        l_history[i] =  loss_function(X,y,w,b) # 梯度下降过程中的损失
        print ("轮次", i+1 , "当前轮训练集损失：",l_history[i]) 
        w_history[i] = w # 梯度下降过程中权重的历史 请注意w_history和w的形状
        b_history[i] = b # 梯度下降过程中偏置的历史
    return l_history, w_history, b_history

下面进行实战案例。

二、通过逻辑回归解决二元分类问题

数据集可以在kaggle的Datasets页面搜索关键词heart就可以找到它。

1.数据的准备与分析

1.数据读取

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
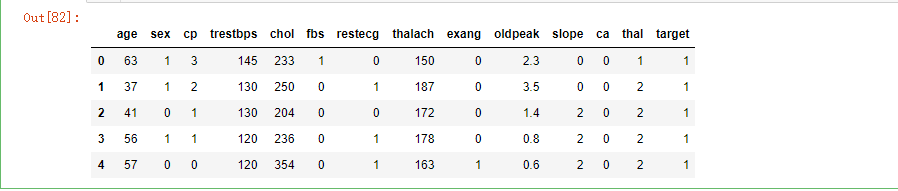
df_heart = pd.read_csv(r'E:\Users\lenovo\Desktop\心脏病\数据集/heart.csv')
df_heart.head()

用values_counts方法输出数据中患心脏病和没有心脏病的人数：

df_heart.target.value_counts()

还可以对某些数据进行相关性的分析，例如可以显示年龄/最大心率这两个特征与是否患病之间的关系：

plt.scatter(x=df_heart.age[df_heart.target==1],
           y = df_heart.thalach[(df_heart.target==1)],c= 'red')
plt.scatter(x = df_heart.age[df_heart.target == 0],
           y = df_heart.thalach[(df_heart.target == 0)], marker='^')
plt.legend(['Disease','No Disease'])#显示图例
plt.xlabel('age')
plt.ylabel('Heart Rate')
plt.show()

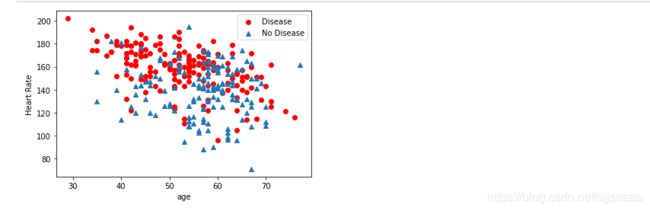
输出结果显示出心率越高，患心脏病的可能性看起来很大，因为代表患病样本的圆点，多集中于图的上方。

2.构建特征集和标签集

#构建特征集和标签集
X = df_heart.drop(['target'],axis=1)  #构建特征集
y = df_heart.target.values #构建标签集
y = y.reshape(-1,1) 
print("张量X的形状",X.shape)
print("张量y的形状",y.shape)

3.拆分数据集

按照80%/20%的比例准备训练集和测试集：

#差分训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=0)

4.数据特征缩放

这里直接调用sklean 库中的数据缩放器。将数据进行归一化处理。

#将数据特征缩放
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

注意：针对X_trian使用fit_transform(先拟合在应用)，针对X_test使用transform(直接应用)

归一化不一定会提高模型的准确率，时间才是检验真理的唯一标准。

2.建立逻辑回归模型

1.逻辑函数的定义

首先定义一个Sigmoid函数，一会调用：

# 首先定义一个Sigmoid函数，输入Z，返回y'
def sigmoid(z):    
    y_hat = 1/(1+ np.exp(-z))
    return y_hat    

2.损失函数的定义

def loss_function(X,y,w,b):
    y_hat = sigmoid(np.dot(X,w) + b) # Sigmoid逻辑函数 + 线性函数(wX+b)得到y'
    loss = -(y*np.log(y_hat) + (1-y)*np.log(1-y_hat)) # 计算损失
    cost = np.sum(loss) / X.shape[0]  # 整个数据集平均损失    
    return cost # 返回整个数据集平均损失

有了这个函数，无论是训练集还是测试集，输入任意一组参数w和b，都会返回针对当前数据集的平均误差值（损失或成本），这个值我们会一直监控它，直到它收敛到最小。

3.梯度下降的实现

下面构建梯度下降的函数，这也是震哥哥逻辑回归模型的核心代码。这个函数共6个输入参数，除了模型内部参数w,b，数据集X,y之外，还包括两个超参数，学习速率lr(也就是alpha )和迭代次数iter：

# 然后构建梯度下降的函数
def gradient_descent(X,y,w,b,lr,iter) : #定义逻辑回归梯度下降函数
    l_history = np.zeros(iter) # 初始化记录梯度下降过程中误差值(损失)的数组
    w_history = np.zeros((iter,w.shape[0],w.shape[1])) # 初始化权重记录的数组
    b_history = np.zeros(iter) # 初始化记录梯度下降过程中偏置的数组  
    for i in range(iter): #进行机器训练的迭代
        y_hat = sigmoid(np.dot(X,w) + b) #Sigmoid逻辑函数+线性函数(wX+b)得到y'
        loss = -(y*np.log(y_hat) + (1-y)*np.log(1-y_hat)) # 计算损失
        derivative_w = np.dot(X.T,((y_hat-y)))/X.shape[0]  # 给权重向量求导
        derivative_b = np.sum(y_hat-y)/X.shape[0] # 给偏置求导
        w = w - lr * derivative_w # 更新权重向量，lr即学习速率alpha
        b = b - lr * derivative_b   # 更新偏置，lr即学习速率alpha
        l_history[i] =  loss_function(X,y,w,b) # 梯度下降过程中的损失
        print ("轮次", i+1 , "当前轮训练集损失：",l_history[i]) 
        w_history[i] = w # 梯度下降过程中权重的历史 请注意w_history和w的形状
        b_history[i] = b # 梯度下降过程中偏置的历史
    return l_history, w_history, b_history

w_history和b_history返回迭代过程中的历史记录。

4.分类预测的实现

先定义一个负责分类预测的函数：

def predict(X,w,b): # 定义预测函数
    z = np.dot(X,w) + b # 线性函数
    y_hat = sigmoid(z) # 逻辑函数转换
    y_pred = np.zeros((y_hat.shape[0],1)) # 初始化预测结果变量  
    for i in range(y_hat.shape[0]):
        if y_hat[i,0] < 0.5:
            y_pred[i,0] = 0 # 如果预测概率小于0.5，输出分类0
        else:
            y_pred[i,0] = 1 # 如果预测概率大于0.5，输出分类0
    return y_pred # 返回预测分类的结果

这个函数就通过预测概率阈值0.5，把y_hat转换成y_pred，也就是i把一个概率值转成0或1 的分类值。y_pred是一个和y标签集 同样维度的向量，通过比较y_pred和真值就可以看出多少个预测正确，多少个预测错误。

我们可以直接嗲用gradient_descent进行机器的训练，返回损失、最终的参数值：

#分裂预测的实现

loss_function, weight_history,bias_history = gradient_descent(X_train,y_train,weight,bias,alpha,iteration)

但现在还不着急进行训练。

3.开始训练机器

把上面的内容分装成一个逻辑回归模型：

#定义逻辑回归模型

def logistic_regression(X,y,w,b,lr,iter): # 定义逻辑回归模型
    l_history,w_history,b_history = gradient_descent(X,y,w,b,lr,iter)#梯度下降
    print("训练最终损失:", l_history[-1]) # 打印最终损失
    y_pred = predict(X,w_history[-1],b_history[-1]) # 进行预测
    traning_acc = 100 - np.mean(np.abs(y_pred - y_train))*100 # 计算准确率
    print("逻辑回归训练准确率: {:.2f}%".format(traning_acc))  # 打印准确率
    return l_history, w_history, b_history # 返回训练历史记录

代码中的变量traning_acc，计算出了分类的准确率，对于分类问题而言，准确率也急速和i正确预测数相对于全部样本数的比例，这是最基本的评估指标。

训练机器之前，准备参数的初始值：

#初始化参数
dimension = X.shape[1] # 这里的维度 len(X)是矩阵的行的数，维度是列的数目
weight = np.full((dimension,1),0.1) # 权重向量，向量一般是1D，但这里实际上创建了2D张量
bias = 0 # 偏置值
#初始化超参数
alpha = 1 # 学习速率
iterations = 500 # 迭代次数

调用逻辑回归模型，训练机器：

# 用逻辑回归函数训练机器
loss_history, weight_history, bias_history =  logistic_regression(X_train,y_train,weight,bias,alpha,iterations)

训练过程十分顺利，损失随着迭代次数的上升逐渐下降，最后呈现收敛状态，训练500次之后的准确率为83.06%，还算不粗哦。

4.预测分类结果

得到了上面的准确率还不能说明模型的泛化能力，我们要在准备好的测试集中对这个模型进行真正的检验：

y_pred = predict(X_test,weight_history[-1],bias_history[-1]) # 预测测试集
testing_acc = 100 - np.mean(np.abs(y_pred - y_test))*100 # 计算准确率
print("逻辑回归测试准确率: {:.2f}%".format(testing_acc))

查看具体的预测值：

print("逻辑回归预测分类值\n",predict(X_test,weight_history[-1],bias_history[-1]))

5.绘制损失曲线

还可以绘制出针对训练集和测试集的损失曲线：

#绘制损失曲线
loss_history_test = np.zeros(iterations) # 初始化历史损失
for i in range(iterations): #求训练过程中不同参数带来的测试集损失
    loss_history_test[i] = loss_function(X_test,y_test,
                                         weight_history[i],bias_history[i])
index = np.arange(0,iterations,1)
plt.plot(index, loss_history,c='blue',linestyle='solid')
plt.plot(index, loss_history_test,c='red',linestyle='dashed')
plt.legend(["Training Loss", "Test Loss"])
plt.xlabel("Number of Iteration")
plt.ylabel("Cost")
plt.show() # 同时显示显示训练集和测试集损失曲线

可以明显的看到在迭代80-100次后，训练集的损失进一步下降，越来越小，但是测试集的损失并没有跟着下降，反而显示呈上升趋势，明显的过拟合现象，因为此迭代应该在100次前结束。

因此，损失曲线告诉我们，对于这个案例，最佳迭代次数是80-100次，才能让训练集和测试集都达到比较好的预测效果。这是模型在训练集上面优化，在测试集上泛化 的一个折中方案。

6.直接调用sklearn 库

上面的方法是为了理解逻辑回算法实现的细节，当我们真正使用的时候两三行代码就可以实现：

from sklearn.linear_model import LogisticRegression #导入逻辑回归模型
lr = LogisticRegression() # lr,就代表是逻辑回归模型
lr.fit(X_train,y_train) # fit,就相当于是梯度下降
print("SK-learn逻辑回归测试准确率{:.2f}%".format(lr.score(X_test,y_test)*100))

这里的ift方法就相当于我们前面费力气编写的梯度下降代码。

7.特征工程——哑特征的使用

观察’cp’'thal’这样的数据，他们也都代表类别，比如cp这个字段意义是”胸痛类别“,取值为0，1，2，3的话计算机会理解为数值，进行对比，认为3比2大，2比1大。所以这样是不科学的，因为这种类别值只是一个代号，它的意义和年龄、身高这种连续值的意义是不同的。

所以我们把这种类别特征拆分成多个哑特征，比如cp有0，1，2，3这四个类，就拆分成四个特征，cp_0为一个特征，cp_1为一个特征，cp_2为一个特征,cp_3为一个特征，每一个特征都还原成二分类，答案是Yes或者No，也就是1和0.

用python做特征工程哑特征：

a = pd.get_dummies(df_heart['cp'],prefix='cp')#将文本型变量转成哑变量
b = pd.get_dummies(df_heart['thal'],prefix='thal')
c = pd.get_dummies(df_heart['slope'],prefix='slope')

frames = [df_heart,a,b,c]#把哑变量填进dataframe
df_heart = pd.concat(frames,axis=1)
df_heart#显示新的dataframe

三、从二元分类到多元分类

在实际生活中，分类不总是二元的，多元分类就是多个类别，而且每一个类别和其他类别都是互斥的情况，也就是说，最终所预测的标签只能属于多个类别中的某一个。

1.以一对多

就是说，有多少类别，就要训练多少二元分类器。每次u西安则一个类别作为正例，为1，其他所有类别都视为负例，为0，以此类推至所有的类别。

训练好多个二元分类器之后，做预测时，将所有的二元分类器都运行一遍，然后对每一个输入样本，选择最高可能性的输出概率，即为该样本多元分类的类别。

还有一种分类叫做”多标签分类“，指的是如果每种样本可以分配多个标签，就称为多标签分类。

2.多元分类的损失函数

多元分类的损失函数的选择与输出编码，与标签的格式有关
有两种格式：

• 一种是one-hot格式的分类编码，比如0-9中的8，格式为[0,0,0,0,0,0,0,1,0].
• 一种是直接转换为类别数字，如1，2，3，4

因此损失函数也有两种情况：

• 如果通过one-hot分类编码输出标签，则应使用分类交叉熵作为损失函数。
• 如果输出的标签编码为类别数字，则应使用系数分类交叉熵作为损失函数。

四、正则化、欠拟合和过拟合

1.正则化

机器学习中的正则化是在损失函数里面加惩罚项，增加建模的模糊性，从而把捕捉到的趋势从局部细微趋势，调整到整体大概趋势，虽然一定程度上地放宽了建模要求，但是能有效防止过拟合的问题，增加模型的准确性，它影响的是模型的权重。

regularization、normalization和standardization这三个单词看起来相似，常常混淆。标准化、规范化、归一化，是调整数据，特征缩放；而正则化，是调整模型，约束权重。

2.欠拟合和过拟合

正则化技术索要解决的过拟合问题，连同欠拟合一起，都是机器学习模型调优、参数调试过程中的主要阻碍。

一开始模型很烂的时候，训练集和测试集的误差都很大，这是欠拟合。
随着模型的优化，训练集和测试集的误差都有所下降，其中训练集的误差值要比测试集的低。
但如果此处继续增加模型对训练集的拟合程度，会发现测试集的误差将逐渐提高，这个过程就是过拟合。

所以，过拟合就是机器学习的模型过于依附与训练集的特征，因而模型的泛化能力降低的体现。
泛化能力，就是模型从训练集移植到其他数据集仍能够完成预测的能力。

过拟合现象是机器学习过程中怎么甩都甩不掉的阴影。

降低过拟合的方法：

• 增加数据集的数据个数
• 找到模型优化时的平衡点，比如，选择迭代次数，或者选择相对简单的模型。
• 正则化。为可能出现过拟合现象的模型增加正则项，通过降低模型在训练集上的精度来提高其泛化能力。

3.正则化参数

机器学习中的正则化引入模型参数λ来实现。损失函数更新：

现在的训练优化算法是一个由两项内容组成的函数：一个是损失项，用于衡量模型与数据的拟合度；另一个是正则化项，用于调解模型的复杂度。

正则化的本质：就是崇尚简单化。同时以最小化损失和复杂度为目标，这称为结构风险最小化。

选择λ值的目标是在简单化和训练集数据拟合之间达到适当的平衡。

• 如果λ过大， 则模型会非常简单，将面临数据欠拟合的风险，值越大，机器收敛越慢。
• 如果λ过小，则模型会非常复杂，将面临数据过拟合的风险。
• 如果λ为0可彻底取消正则化，在这种情况下，训练的唯一目的就是最小化损失，此时过拟合的风险较高。

正则化参数通常以偶L1正则化和L2正则化两种选择：

• L1正则化，根据权重的绝对值的综合来惩罚权重，在依赖稀疏特征的模型中，L1正则化会有助于使不相关或者几乎不想管的特征权重正好为0，从而将这些特征从模型中移除
• L2正则化，根据权重的平方和来逞罚全中，L2正则化有助于使离群值的权重接近于0，但又不会正好为0，在线性模型中，L2正则化比较常用，而且在任何情况下都能够起到增强泛化能力的目的。

正则化不仅可以应用于逻辑回归模型，也可以应用于线性和其他机器学习模型，应用L1正则化的回归交嵌套回归（Lasso Regression），应用于L2正则化的回归又叫岭回归（Ridge Regression）

而最佳的λ值取决于具体数据集，需要手动或者自动进行调整。

五、通过逻辑回归解决多元分类问题

1.数据的准备与分析

鸢尾花数据集。

from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target

划分训练集和测试集：

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=0)

2.通过sklearn实现逻辑回归的多元分类

from sklearn.linear_model import LogisticRegression  
lrq = LogisticRegression()
lrq.fit(X_train,y_train)
lrq.score(X_test,y_test)  #分数
y_pred = lrq.predict(X_test)#预测值
y_pred

采用L2正则化和c参数：

lrw = LogisticRegression(penalty='l2',C=10)
lrw.fit(X_train,y_train)
lrw.score(X_test,y_test)

3.正则化参数——C值的选择

用绘图的方式显示出采用不用的C，对于鸢尾花分类边界的具体影响。

首先定义一个绘图的函数：

import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
def plot_decision_regions(X,y,classifier,test_idx=None,resolution=0.02):    
    markers = ('o','x','v')
    colors = ('red','blue','lightgreen')
    color_Map = ListedColormap(colors[:len(np.unique(y))])     
    x1_min = X[:,0].min() - 1
    x1_max = X[:,0].max() + 1
    x2_min = X[:,1].min() - 1
    x2_max = X[:,1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),
                           np.arange(x2_min,x2_max,resolution))    
    Z = classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)    
    plt.contour(xx1,xx2,Z,alpha=0.4,cmap = color_Map)
    plt.xlim(xx1.min(),xx1.max())
    plt.ylim(xx2.min(),xx2.max())   
    X_test, Y_test = X[test_idx,:], y[test_idx]
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x = X[y == cl, 0], y = X[y == cl, 1],
                    alpha = 0.8, c = color_Map(idx),
                    marker = markers[idx], label = cl)

然后使用不同的C值进行逻辑回归分类，并绘制分类结果：

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
C_param_range = [0.01,0.1,1,10,100,1000]
petal_acc_table = pd.DataFrame(columns = ['C_parameter','Accuracy'])
petal_acc_table['C_parameter'] = C_param_range
plt.figure(figsize=(10, 10))
j = 0
for i in C_param_range:
    lr = LogisticRegression(penalty = 'l2', C = i,random_state = 0)
    lr.fit(X_train_petal,y_train_petal)
    y_pred_petal = lr.predict(X_test_petal)
    petal_acc_table.iloc[j,1] = accuracy_score(y_test_petal,y_pred_petal)
    j += 1    
    plt.subplot(3,2,j)
    plt.subplots_adjust(hspace = 0.4)
    plot_decision_regions(X = X_combined_petal, y = Y_combined_petal, 
                          classifier = lr, test_idx = range(105,150))
    plt.xlabel('Petal length')
    plt.ylabel('Petal width')
    plt.title('C = %s'%i)

可以看到：

• C取值越大，分类精度越大
• C取值过于小，正则化的力度过大，为了追求泛化效果，算法可能会失去区分度。

小结

线性回归用于解决回归问题（可简单理解为数值预测问题），逻辑回归多用于解决分类的问题。

在目前的数据科学家工组中，线性回归和逻辑回归的使用率还是很高的，因为这两种算法可以快速应用，作为其他解决方案的基准模型。