深度学习评估指标之目标检测——(yolov5 可视化训练结果以及result.txt解析)
1、机器学习模型评估指标总结
机器学习的数据集一般被划分为训练集和测试集,训练集用于训练模型,测试集则用于评估模型。针对不同的机器学习问题(分类、回归、排序、序列预测等),评估指标决定了我们如何衡量模型的好坏。
1、分类任务评估指标
下面的一些是经常用来评价模型好坏的一些指数:准确率、精确率、召回率、F1 Score、P-R曲线、ROC、AUC。


一、Accuracy
这个指标主要是用来指示预测正确的样本数占总样本数的个数。准确率是最简单的评价指标,公式如下:


但是存在明显的缺陷:
当样本分布不均匀时,指标的结果由占比大的类别决定。比如正样本占 99%,只要分类器将所有样本都预测为正样本就能获得 99% 的准确率。
结果太笼统,实际应用中,我们可能更加关注某一类别样本的情况。比如搜索时会关心 “检索出的信息有多少是用户感兴趣的”,“用户感兴趣的信息有多少被检测出来了” 等等。
相应地还有错误率:分类错误的样本占总样本的比例。
from sklearn.metrics import accuracy_score
y_pred = [0, 0, 1, 1]
y_true = [1, 0, 1, 0]
accuracy_score(y_true, y_pred) # 0.5
二、Precision(P)、 Recall® 、 F1
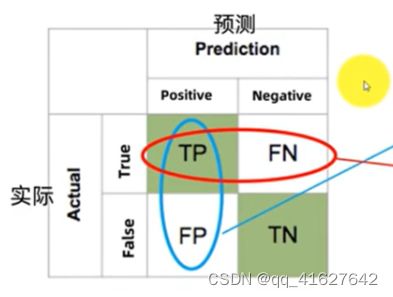
精准率(Precision)也叫查准率,衡量的是所有预测为正例的结果中,预测正确的(为真正例)比例。精度Precision(查准率)是评估预测的准不准(看预测列)

召回率(Recall)也叫查全率,衡量的是实际的正例有多少被模型预测为正例。召回率Recall (查全率)是评估找的全不全(看实际行)

精确率和召回率是一对相互矛盾的指标,一般来说高精准往往低召回,相反亦然。其实这个是比较直观的,比如我们想要一个模型准确率达到 100%,那就意味着要保证每一个结果都是真正例,这就会导致有些正例被放弃;相反,要保证模型能将所有正例都预测为正例,意味着有些反例也会混进来。这背后的根本原因就在于我们的数据往往是随机、且充满噪声的,并不是非黑即白。
为了获得模型优劣,需要综合 P 和 R,平衡点 BEP(Break-Even Point)就是这样一个度量,它是 P=R 时的取值,BPE 越远离原点,说明模型效果越好。由于 BPE 过于简单,实际中常用 F1 值衡量:


三、P-R曲线
在分类时,我们经常需要对学习模型的预测结果进行排序,排在前面的被认为“最可能”是正类样本,排在后面的被认为“最不可能”是正类样本。因此我们往往要在中间设定一个临界值(Threshold),当预测值大于这个临界值时,样本为正类样本,反之为负类样本。
按不同的临界值,将每个样本作为正类样本来预测,就会得到不同的查准率和查全率。如果以查准率为纵轴,以查全率为横轴,那么每设定一个临界值,就可以在坐标系上画出一个点。当设定多个临界值时,就可以在坐标系中画出一条曲线。这条曲线便是 P-R 曲线,如图所示。

P-R 曲线能直观地显示分类算法在整体上的查准率和查全率。当对多个分类算法进行比较时,如果算法 1 的 P-R 曲线完全“外包围”算法 2 的 P-R 曲线,那么处于外侧的算法 1 有着更高的查准率和查全率(双高),这说明算法 1 比算法 2 有着更好的分类性能。
但更一般的情况是,算法之间的 P-R 曲线彼此犬牙交错(见图 1),很难断言二者孰优孰劣,只能在具体的查准率和查全率下做比较。但倘若非要比个高下,该怎么办呢?比较稳妥的办法是比较 P-R 曲线下的面积大小,谁的面积大,从某种程度上就说谁的“双高”比例大,即性能更优
得到 P 和 R 后就可以画出更加直观的P-R 图(P-R 曲线),横坐标为召回率,纵坐标是精准率。绘制方法如下:
from typing import List, Tuple
import matplotlib.pyplot as plt
def get_confusion_matrix(
y_pred: List[int],
y_true: List[int]
) -> Tuple[int, int, int, int]:
length = len(y_pred)
assert length == len(y_true)
tp, fp, fn, tn = 0, 0, 0, 0
for i in range(length):
if y_pred[i] == y_true[i] and y_pred[i] == 1:
tp += 1
elif y_pred[i] == y_true[i] and y_pred[i] == 0:
tn += 1
elif y_pred[i] == 1and y_true[i] == 0:
fp += 1
elif y_pred[i] == 0and y_true[i] == 1:
fn += 1
return (tp, fp, tn, fn)
def calc_p(tp: int, fp: int) -> float:
return tp / (tp + fp)
def calc_r(tp: int, fn: int) -> float:
return tp / (tp + fn)
def get_pr_pairs(
y_pred_prob: List[float],
y_true: List[int]
) -> Tuple[List[int], List[int]]:
ps = [1]
rs = [0]
for prob1 in y_pred_prob:
y_pred_i = []
for prob2 in y_pred_prob:
if prob2 < prob1:
y_pred_i.append(0)
else:
y_pred_i.append(1)
tp, fp, tn, fn = get_confusion_matrix(y_pred_i, y_true)
p = calc_p(tp, fp)
r = calc_r(tp, fn)
ps.append(p)
rs.append(r)
ps.append(0)
rs.append(1)
return ps, rs
y_pred_prob = [0.9, 0.8, 0.7, 0.6, 0.55, 0.54, 0.53, 0.52, 0.51, 0.505,
0.4, 0.39, 0.38, 0.37, 0.36, 0.35, 0.34, 0.33, 0.3, 0.1]
y_true = [1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0]
y_pred = [1] * 10 + [0] * 10
ps, rs = get_pr_pairs(y_pred_prob, y_true)
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(12, 5))
ax.plot(rs, ps);
如果有多个模型就可以绘制多条 P-R 曲线:
如果某个模型的曲线完全被另外一个模型 “包住”(即后者更加凹向原点),那么后者的性能一定优于前者。
如果多个模型的曲线发生交叉,此时不好判断哪个模型较优,一个较为合理的方法是计算曲线下面积,但这个值不太好估算。
四、ROC曲线
针对样本不均衡,以上 Precision、Recall、F1都很高,但是模型效果却不好,指标很难区分模型的性能,就需要用到ROC和AUC。
ROC 曲线是通过不断移动分类器的“截断点”来生成曲线上一系列关键点的。下面我们来解释“截断点”。很多时候,我们在判断某个样本是正类样本还是负类样本时,并不能“斩钉截铁”地说它“是(100%)”或“不是(0%)”。
很多分类器(比如贝叶斯分类器、神经网络分类器)仅仅会输出一个分类概率,这时可以给定一个截断点(或说阈值概率),如果分类概率大于这个截断点就判断样本为是正类样本,否则就为负类样本。对于一个已经排序的分类概率,不断移动分类器的“截断点”就会生成曲线上的一系列关键点 (FPR,TPR)。这些关键点连接起来恰好就是一条曲线,它就是我们正在学习的 ROC 曲线
引入两个公式TPR(真阳性率)和FPR(假阳性率)
真正类率(true positive rate, TPR),也称为灵敏度(sensitivity),等同于召回率。刻画的是被分类器正确分类的正实例占所有正实例的比例。

真负类率(true negative rate, TNR),也称为特异度(specificity),刻画的是被分类器正确分类的负实例占所有负实例的比例。

负正类率(false positive rate, FPR),也称为1-specificity,计算的是被分类器错认为正类的负实例占所有负实例的比例。


理想目标: TPR=1, FPR=0,即图中(0,1)点。故ROC曲线越靠拢(0,1)点,即,越偏离45度对角线越好。对应的就是TPR越大越好,FPR越小越好。
五、AUC
AUC 是 Area Under Curve 的简称,顾名思义,它表示的是“ROC曲线下的面积”。AUC 就是 ROC 曲线下的面积总和,该值能够量化反映分类算法的性能。
计算 AUC 的值并不复杂,只需要沿着 ROC 曲线的横轴做积分(或累加求和)即可。通常,ROC 曲线都位于 y=x 这条线的上方(如果不是这样的,只需要把模型预测概率 P 反转成 1-P 能得到一个更好的分类器)。
因此,AUC 的取值范围一般是 0.5~1。通常来说,AUC 越大表明分类器性能越好,因为它可以把真正的正类样本排在前面,降低误判率。
2、回归任务评估指标
一、均方根称RMSE(Root M Square Error)
计算公式为:
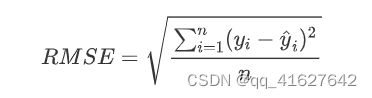
如果有非常严重的离群点时,那些点会影响 RMSE 的结果,针对这个问题:
如果离群点为噪音,则消除这些点
如果离群点为正常样本,可以重新建模
平均误差范围内,MAPE(平均百分比误差)对每个范围进行了一定程度的影响。
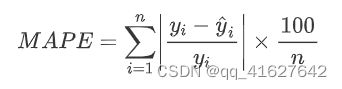
二、平均绝对误差 Mean Absolute Error

平均绝对误差是一个非常直观的指标。它是预测值和真实值之间的平均距离。为了避免错误相互抵消,取计算绝对值。最好的模型通常是 MAE 最低的模型。
尽管解释起来很简单,但 MAE 有一些缺点。它不会告诉模型是否倾向于高估或低估,因为取绝对值会破坏任何方向信息。此外,该指标可能对异常值不敏感
2、深度学习模型评估指标总结
一、性能评估指标
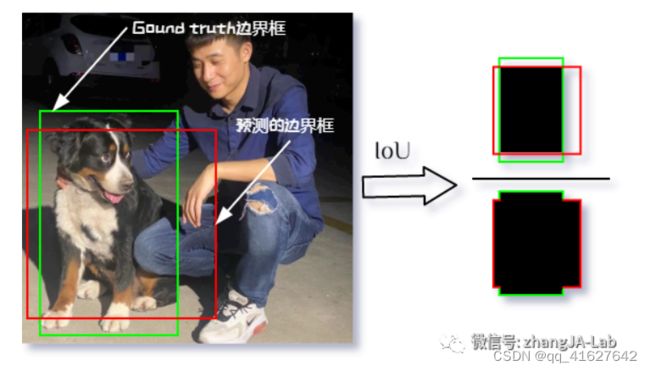
1、IOU(Intersection over Union )
交并比(IoU)则表示预测的边界框与真实(Ground Truth)的边界框的重叠程度,数值越大表示该检测器的性能越好。

2、AP (Average Precision)
3、mAP
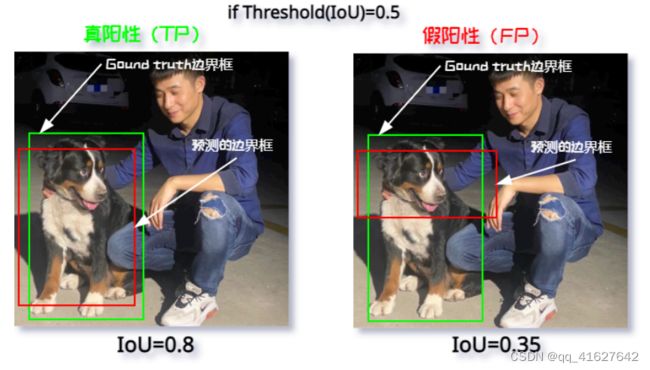
在目标检测任务中,结合上面讲的 IoU 阈值来判断其真阳性(TP)、假阳性(FP),从而来计算精度(Precision),比如:
要计算 mAP,首先要计算每个类别的 AP。所有类的 AP 的平均值是 mAP。如下步骤:
① 使用模型生成预测分数;
② 将预测分数转换为类标签;
③ 计算其混淆矩阵 - TP FP TN FN;
④ 计算精度(P|Precision)以及召回率(R|Recall);
⑤ 画出 P-R 的曲线,并计算 P-R 曲线下的面积;
⑥ 计算平均精度(AP)。
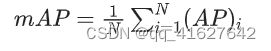
从上面的计算方式,我们可以看出:mAP 结合了精度(Precision)和召回率(Recall)之间的权衡,并考虑了假阳性(FP)和假阴性(FN),故而此属性使得 mAP 成为了大多数检测模型性能的合理评价指标。

我们再重新过一遍计算方法:给定一组IOU阈值,在每个IOU阈值下面,求所有类别的AP,并将其平均起来,作为这个IOU阈值下的检测性能,称为mAP(比如[email protected]就表示IOU阈值为0.5时的mAP);最后,将所有IOU阈值下的mAP进行平均,就得到了最终的性能评价指标:mmAP。

4、平均对数漏检率(log-average miss rate)
平均对数漏检率(log-average miss rate)常用的行人检测评价指标,均是目前主流的判断行人检测器优劣的标准。
- 平均对数漏检率(log-average miss rate) (Dollár等,2012)。该指标通过同时计算MR(miss rate)和每幅图误检个数(false positives per image,FPPI)衡量行人检测器性能。MR计算为
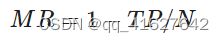
式中,TP(true positive)表示预测正确的行人目标个数,N表示真实行人目标总数。通过绘制MR-FPPI曲线,平均对数漏检率为9个FPPI值下的平均MR值,记为MR-2,其中9个点是对数区间[10-2, 100]上的均匀采样。MR-2表示在指定误检率的情况下行人检测器的漏检率。MR-2越低,表示模型漏检率越低,检测性能越好。
FPPI(False Positive Per Image)描述每张图片的平均误检率。假设有N张图片,结果中的误检数量为FP,则
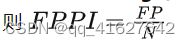
MR(Miss Rate)描述检测检测结果中的漏检率的指标,即 ,该指标越小越好 。

MR-FPPI与目标检测所用的Precious-Recall类似,都是两个互斥的指标,一个性能的提升必然会带来另一个性能的下降,可以反映检测器的整体性能。由于在行人检测中每幅图像的FPPI上限与行人的密度有关系,所以在行人检测领域采用MR-FPPI曲线比Precious-Recall曲线更加合理。
采用FPPI为横坐标, 为纵坐标的曲线中,均匀选取 范围内的9个FPPI,得到他们对应的9个值,并对这几个纵坐标值进行平均,最后通过指数运算上述平均值恢复为MR的百分比形式,就获得了用来量化MR-FPPI曲线的 指标,该指标越小代表检测器性能越高
关于 这个指标,有一些详细的内容要记录,首先自己做了快一年的行人检测,也是最近才弄懂这个指标的含义。具体的理解还得参照这篇论文Pedestrian Detection: An Evaluation of the State of the Art
3、yolov5 可视化训练结果以及result.txt解析
1.可视化训练结果解析
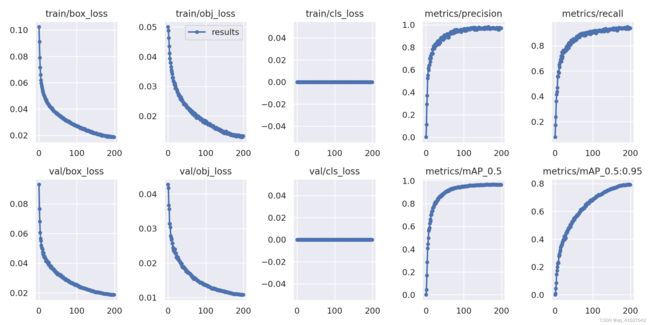
box_loss:推测为GIoU损失函数均值,越小方框越准;
obj_loss:推测为目标检测loss均值,越小目标检测越准;
cls_loss:推测为分类loss均值,越小分类越准;
Precision:精度(找对的正类/所有找到的正类);
Recall:召回率(找对的正类/所有本应该被找对的正类);
[email protected] & [email protected]:0.95:就是mAP是用Precision和Recall作为两轴作图后围成的面积,m表示平均,@后面的数表示判定iou为正负样本的阈值,@0.5:0.95表示阈值取0.5:0.05:0.95后取均值。
一般训练结果主要观察精度和召回率波动情况.
(波动不是很大则训练效果较好)
然后观察[email protected] & [email protected]:0.95 评价训练结果