迷宫问题构思
背景:
交通运输是支撑国民经济发展的重要产业,承担着促进商品的高效快捷流转的使命,物流行业在现代社会发展中有着十分积极的作用,在新的时代背景下物流业需要更加智能化的管理与服务模式。“智慧物流”起源于IBM提出的“智慧地球”这一概念,经过我国政府“感知中国”、“互联网+物流”建设战略,智慧物流迅速崛起。智慧物流可以深入推动供应链整合升级,促进物流行业创新发展与结构调整,为物流行业在影响社会生产与物资流通的同时,转变产业发展方式以满足客户多元化的需求,促进产品流通。
随着社会发展 , 物流智能化 , 迷宫问题也呈现眼前 , 如何让快递 在一瞬间找到能够通往指定位置的路线呢?
这就延伸到了我们的迷宫问题 .下面开始我们的构思:
在一瞬间找出通路 , 在强大的算力面前当然是可能的 , 但是需要我们赋予机器算法 , 让其通过固定的程序运算 ,即可得出通路.
我们先通过大脑模拟 ,来实现找出通路:
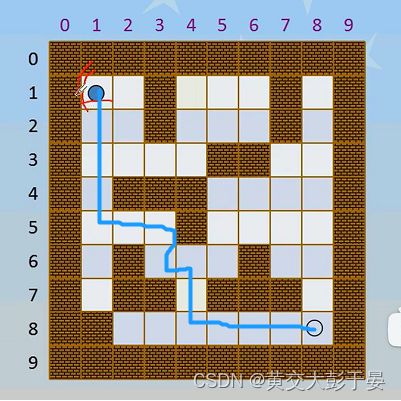
从(1,1)出发 ,目标是左下角 , 直接看见了一条同路, 往下走 , 然后从终点往回走 , 看见两条通路 ,都可以通过唯一的入口,然后下面的
一条路最短, 果断选择
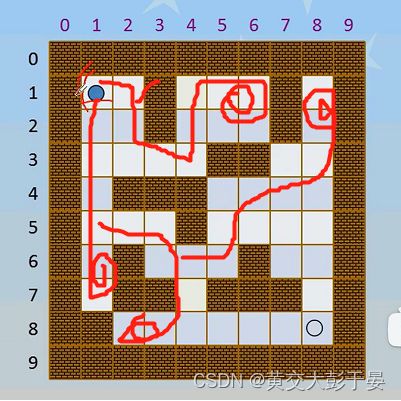
左图 ,当然是人脑进行运算的最短路径 , 右边则是机器通过固定运算而可能得到的不同的路径的.
python 之父说过: 人类大脑才是软件开发效率的天花板
既然机器只会 朝着固定的方向遍历查找 ,那么我们就想一个办法,一定能到达终点的办法
根据迷宫的特性 , 从一个节点出发 ,可以走向不同的方向 , 形成不同路线和分支 , 但是并不是所有路线都是有解的.
因为现在我们只有一个机器 , 所以到了死胡同 ,就需要往回走了,回到上一个节点,然后选择另一个方向继续寻找
这样有解吗?
答案是: 只要迷宫有解 , 那我们这个算法就一定能找出出口 , 因为就算我们第一步就选择错了方向 ,仍能回溯到起点,然后进行下一个方向的移动,直到成功.
我们找到出口可以选择两个极端的办法:
①我们有足够的人力资源, 从起点开始 , 让所有探索者出发 ,通往不同的路线 ,我们会把所有路线全部遍历 ,总能遍历到有解路线
② 我们只有一个人 , 从起点开始 , 遍历一个节点的一个方向 ,然后直到死胡同 ,然后再返回上一个节点的下一个方向 ,直到有解.
方法一: 占用的空间复杂度比较大
方法二: 占用的时间复杂度比较大
我们当然不会对这两种极端情况给予期待,我们所关注是是平均算法复杂度,
我们关注的是,在最优解的路线上,有几个分叉路口,有几次我们与正确答案擦肩而过,这些与正确答案擦肩而过的路口 和 所有路线的所有路口图所形成的比例,就是我们成功的概率,这是我们所关注的点
通俗的讲,就是我们在返回路线的时候,如果恰好返回到最优解路线的路口,那么这就极大增加了我们成功的概率
那按照计算机的日常操作,我们就采用折中的算法,先算出一个有几条路线,然后派一半的人,甚至四分之一的人,去探索,他们之间共享同一个路线数据,访问过的路线就不需要其他人来访问,这样应该是可行的办法
由于作者能力有限 , 我们现在先进行深度优先遍历 ,一次直走一条路线 ,走到头的话 ,回退到路线的上一个节点 ,然后选择另一个方向,
直到成功
既然我们要遍历迷宫的路线 ,首先先把环境搭建好 , 我们通常的做法是 把迷宫的地图画出来 ,我们在程序内 ,只需要把每个坐标节点,用数组存储就行了
我们要存储数组 ,就要知道数组的特性 , 涉及到二维数组 ,我们第一个字符代表一行 ,第二个字符代表一行的第几列 ,我们设 x 为行数 ,y 为列数(具体问题具体分析)
然后,现在我们要从初始地点(1,1) 进行出发 ,那往哪个方向出发呢? 那个方向优先级最高呢?
对于我们人类来说 , 哪个最近那个先出发 ,但是机器遍历每个节点的每个方向都是固定程序 ,不按照特定方向顺序 ,有可能错乱
我们就先定节点的结构体 来反映每个节点的坐标 和每个结点要走的方向 ,至于可走那个方向 ,需要程序判断
typedef struct { int x; int y; int di; }Box;
节点的方向有了 ,下面开始我们的主函数调用 ,构思:
int main()
{
//输入初始坐标 和目的坐标;
int m,n,m_1,n_1,m_2; printf("请输入初始地址:\n(例如: 1,1 )"); scanf("%d,%d",&m,&n); printf("请输入出口地址:\n(例如: 8,8 )"); scanf("%d,%d",&m_1,&n_1);//然后调用找出口的函数,输出结果;
m_2 =mgpath(m,n,m_1,n_1);// 并根据返回值 ,判断是否找到有解路径;
if(m_2==1) { printf("输出有解路径"); } else if(m_2 == 0) { printf("无解路径"); } return 0;}
所以找到有解路线,就输出并返回 1 ,无解的话,就返回 0;
下面开始构造寻找迷宫的成员函数:
接下来, 我们需要存储我们走得路线 , 所以需要 用到栈 ,先定义一个顺序栈吧
typedef struct { Box data[MaxSize]; int top; }StType;
传入 出发地址坐标 , 目的地址坐标
int mgpath(int xi,int yi,int xe, int ye) {我们要出发,就要先初始化我们存储路线的数据栈 ,
//定义存储路线节点的数组栈 StType st; //初始化栈顶指针 st.top=-1;
下面我们开始出发:
从出发点出发,所以出发点先入栈
//刚开始要先让出发地址填入 //栈顶加1 st.top++; st.data[st.top].x = xi; st.data[st.top].y = yi;我们已经安全降落了 ,下一步选择方向进行下一个移动并入栈
节点不会自己移动 ,我们需要为每个方向设计一个移动的操作 , 当我们把节点方向调成特定数字时 ,我们就对进行相应的坐标移动操作
设每个加入路线的节点 ,我们初始方向都是向上,然后向右 ,向下 ,向左 ,逐个遍历
我们先为每个方向设置一个 下标 , 上 0 , 右 1, 下 2 , 左 3 ,
此时我们路线已经入栈, 栈顶的元素就是初始方向节点(1,1) ,还未进行方向标明 ,我们记作 -1
st.data[st.top].di = -1;
地图上(1,1)已经被占用 ,标记为 -1
mg[xi][yi] = -1;开始走 ,栈不空时候循环(当我们为栈顶压入初始地时 , 寻找程序即被激活)
while(st.top > -1) {
现在需要判断一个极端情况 , 我们路线的栈顶节点是我们的目的地吗? 如果我们出发地就是目的地 ,那我们就直接输出栈底到栈顶的结点就可以了
(注: 栈的特性 , 先进后出 ,我们需要从出发地开始到目的地的路线 ,所以利用数组的特性 ,从 位序 0 遍历到 栈顶就可以了)
所以先把栈顶元素的地址 和目的地作对比 , 我们先引入一个中间量 ,来指引当前坐标
int i (行坐标), int j (列坐标) , 当前方向 di
i = st.data[st.top].x; j = st.data[st.top].y; di= st.data[st.top].di;
如果栈顶地址和目标地址坐标相等 ,则证明已经到达目的地if(i == xe && j == ye) { printf("迷宫路径如下:\n"); //从数组初始到栈顶元素,栈也是从0开始,位序一致 for(k=0;k<=st.top;k++) { printf("\t(%d,%d),st.data[k].x,st.data[k].y"); if((k+1)%5==0) { printf("\n"); } } printf("\n"); return 1; }如果没通过上述检验 ,就证明 我们还要继续移动遍历
我们从初始节点 ,向四周移动的时候 , 我们先从 上 , 右 , 下 ,左 ,各个方向尝试 ,因为 我们只有一个人,所以我们只能记录一条路线 ,然后走不通再把记录路线的栈 里的节点弹出 ,返回上一个节点,然后遍历上一个节点的下一个方向
所以我们入栈的节点需要包括 ,坐标和 已经走过的方向
如何判断节点的下一个方向是否可通行呢?
我们目前有两种障碍 ,一个是墙壁 ,一个是我们已经入栈的路线的节点, 剩下的就是可通行的点
int mg[X+2][Y+2] ={ {1,1,1,1,1,1,1,1,1,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,0,0,1,1,0,0,1}, {1,0,1,1,1,0,0,0,0,1}, {1,0,0,0,1,0,0,0,0,1}, {1,0,1,0,0,0,1,0,0,1}, {1,0,1,1,0,1,1,1,0,1}, {1,1,0,0,0,0,0,0,0,1}, {1,1,1,1,1,1,1,1,1,1} };
所以,我们要知道栈顶节点所指的方向能否可以通行 ,需要我们进行模拟通行, 然后和数组地图的值进行比较 ,如果是 '0' ,则表示可以通行 ,我们再进行下一步操作 ,如果我们把所有方向都模拟移动了,但还是没找到下一个可走的方块 , 我们就可以把栈顶的元素弹出了 ,栈指针下移,元素地图坐标置成 '0'
标记 find =0; //未找到下一个可通行的节点
find = 0; while(di<4 && find == 0) { di++; switch(di) { case 0: i = st.data[st.top].x; j = st.data[st.top].y-1; break; case 1: i = st.data[st.top].x+1; j = st.data[st.top].y; break; case 2: i = st.data[st.top].x; j = st.data[st.top].y+1; break; case 3: i = st.data[st.top].x-1; j = st.data[st.top].y; break; } //判断地图相应方向的坐标是否可以通行 if(mg[i][j]==0) { find = 1; //标记为找到下一个节点 } }
如果通过模拟 ,栈顶的节点可以找到可走方块 , 则把栈顶节点的方向赋值为可走方块方向
(以便后续如果走不通,可以走节点的下一个方向,走不通则出栈)
if(find == 1) { st.data[st.top].di = di; st.top++; st.data[st.top].x = i; st.data[st.top].y = j; //还不知道下一个可通行的节点,需要通过下一步循环判断 st.data[st.top].di = -1; //栈顶元素已经更新 ,移动到了新节点,相应地图标志被占用'-1', mg[i][j] =-1; } //如果通过上述循环 ,栈顶元素所有方向都没找到可走方块,说明此路不通, //需要退回到上一个栈顶节点,然后遍历其下一个方向 else { mg[st.data[st.top].x][st.data[st.top].y] = 0; st.top--; }
注: 这里出栈元素, 有的同学可能会有疑问 ,我们单纯把地图改了, 这个无可厚非 ,我们路线是用数组承载的 , 我们只是回退了栈顶的指针 , 我们数组里面的元素还没有删除 ,或者是其方向没有改变 后续 我们再次遍历到这个节点的时候, 我们还能走吗?
答案:
能提出这个问题 ,说明大家已经深入想了 , 我们把栈顶元素弹出 ,只是把栈的指针指向数组的上一个位序 , 下次我们再插入的时候 ,我们就会覆盖此节点的数据 ,就算我们没覆盖,我们输出的路线 ,也是从 数组开始 到 栈顶就结束了
弹出的元素还能走吗?
可以的 , 我们变换路线之后 ,可能就把出口让出来的 ,我们走一种路线走不通 ,不代表回退之后 ,下一次路线走不通 , 所以 弹出的节点的坐标 进行必要的初始化是非常有必要的 ,
奈何小编能力有限 ,只是利用数组来存储 , 弹出的数据根本就没保存 ,每次都是初始化 ,所以也就把这个问题 ,巧妙的避开了
思考:
后续我们如果把地图链接起来 ,然后对每个节点进行相应的赋值, 并且判断的话 ,如果弹出走不通的节点 ,必须进行必要的初始化 ,改变路线后 ,那个走不通的节点,说不定就能走通呢?
避免故步自封 .
经过遍历,如果我们通过回溯 ,遍历到某些节点的某些方向,找到了目的地 , 我们就输出路线,返回 1 ,并跳出
break ; return 1;如果我们从出发地, 尝试了所有节点的所有方向 ,还是没有找到通往目的地的方法 ,就返回 错误 0
return 0;
完整代码如下:
#include
#define MaxSize 100
#define X 8
#define Y 8
int mg[X+2][Y+2] ={
{1,1,1,1,1,1,1,1,1,1},
{1,0,0,1,0,0,0,1,0,1},
{1,0,0,1,0,0,0,1,0,1},
{1,0,0,0,0,1,1,0,0,1},
{1,0,1,1,1,0,0,0,0,1},
{1,0,0,0,1,0,0,0,0,1},
{1,0,1,0,0,0,1,0,0,1},
{1,0,1,1,0,1,1,1,0,1},
{1,1,0,0,0,0,0,0,0,1},
{1,1,1,1,1,1,1,1,1,1}
};
typedef struct
{
int x;
int y;
int di;
}Box;
typedef struct
{
Box data[MaxSize];
int top;
}StType;
//传入出发地址和目标地址
int mgpath(int xi,int yi,int xe, int ye)
{
//定义标志功能
int i,j,k,di,find;
//定义存储路线节点的数组栈
StType st;
//初始化栈顶指针
st.top=-1;
//刚开始要先让出发地址填入
//栈顶加1
st.top++;
st.data[st.top].x = xi;
st.data[st.top].y = yi;
//初始方向,设置为-1 ,出发的时候加一(0上,1右,2下,3左)
st.data[st.top].di = -1;
//地图坐标 ,如果位置有节点,就赋值为-1,避免抢占重复
//无节点就是0 ,壁垒就是 1
mg[xi][yi] =-1;
//下面开始走,栈不空时循环,意思就是有节点,我们就可以运行
//初始方块插入栈顶,触发移动机制
while(st.top > -1)
{
//先把插入到栈顶路线的节点和 目标坐标比较,从而判断出是否已经达到目的地
//栈顶节点数据赋值比较,以便后续的操作
i = st.data[st.top].x;
j = st.data[st.top].y;
di = st.data[st.top].di;
//判断是否找到路口,如果找到,输出路径
if(i==xe && j == ye)
{
printf("恭喜你,已经找到出口,路径如下:\n");
//栈里面存放着节点,所以从栈底输出节点坐标即可
//栈也是从 0开始的,所以k小于等于栈顶坐标
for(k = 0; k<=st.top;k++)
{
printf("\t(%d,%d)",st.data[k].x,st.data[k].y);
if((k+1)%5 == 0)
{
printf("\n");
}
}
printf("\n");
return 1;
}
//如果不符合上述条件,则找下一个可走的方块
//来一个标志,标志是否找到下一个可走方块,find(0未找到,1找到)
//进而进行下一步位移操作
find = 0;
//还有方向可走,并且未找到下一个可走方块
while(di<4 && find == 0)
{
//方向加一,进行判断是否找到下一个节点
di++;
//
switch(di)
{
case 0:
i = st.data[st.top].x-1;
j = st.data[st.top].y;
break;
case 1:
i = st.data[st.top].x;
j = st.data[st.top].y+1;
break;
case 2:
i = st.data[st.top].x+1;
j = st.data[st.top].y;
break;
case 3:
i = st.data[st.top].x;
j = st.data[st.top].y-1;
break;
}
if(mg[i][j] == 0)
{
find = 1;
}
//如果上述结点,遍历的方向有通道,就可以走,跳出来,开始去往下一个节点,
//如果已经是最后一个方向,进来之后,也找不到下一个可走方块,赋值为 find=0
}
//找到下一个可走方块,然后进行走动
if(find ==1)
{
//此时说明,我们的坐标 i,j,已经进行了相应的移动,到了新节点上
//下面把路线新节点送到栈内存储
//送到栈顶前,需要把栈顶节点的方向进行更新,赋值成 di,
//老节点向 di 移动,才移动到新节点
st.data[st.top].di = di;
//栈顶指针加一
st.top++;
st.data[st.top].x = i;
st.data[st.top].y = j;
//此时插入了新节点,但是不知道下一个新节点的方向是哪里
//标明 -1 说明,一会移动,从初始化开始
st.data[st.top].di =-1;
//如果通过上述验证,则此节点已经加入路线,占用,标记为-1
mg[i][j] = -1;
}
//如果没找到下一个可以走的路,那就把栈顶的结点拿出来,
//我们换栈顶下的节点,进行下一个方向的探索
else
{
//为了让已经走投无路的节点,下次我们换过路线之后,还能重来
//我们让要出栈的栈顶节点,移动方向初始化,栈顶节点在地图的标号置为0
//注意:我们这里不改变弹出节点的方向,要初始化节点方向
//因为我们用的是数组,所以直接覆盖了节点,但是如果节点数据存在的话,
//我们不能故步自封
st.data[st.top].di = -1; //提醒大家,对节点弹出时,记得初始化方向
mg[st.data[st.top].x][st.data[st.top].y] = 0;
st.top --;
}
}
return 0;
}
int main()
{
int m,n,m_1,n_1,m_2;
printf("请输入初始地址:\n(例如: 1,1 )");
scanf("%d,%d",&m,&n);
printf("请输入出口地址:\n(例如: 8,8 )");
scanf("%d,%d",&m_1,&n_1);
m_2 =mgpath(m,n,m_1,n_1);
if(m_2==1)
{
printf("输出有解路径");
}
else if(m_2 == 0)
{
printf("无解路径");
}
return 0;
}