机器学习——逻辑回归

'''1 Logistic regression
     在这部分的练习中，你将建立一个逻辑回归模型来预测一个学生是否能进入大学。
假设你是一所大学的行政管理人员，你想根据两门考试的结果，来决定每个申请人是否被录取。
你有以前申请人的历史数据，可以将其用作逻辑回归训练集。对于每一个训练样本，你有申请人
两次测评的分数以及录取的结果。为了完成这个预测任务，我们准备构建一个可以基于两次测试
评分来评估录取可能性的分类模型。'''

'''1.1 Visualizing the data
在开始实现任何学习算法之前，如果可能的话，最好将数据可视化。'''
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


data = pd.read_csv('ex2data1.txt', names=['exam1', 'exam2', 'admitted'])
data.head()

positive = data[data.admitted.isin(['1'])]  # 1
negetive = data[data.admitted.isin(['0'])]  # 0

fig, ax = plt.subplots(figsize=(6,5))
ax.scatter(positive['exam1'], positive['exam2'], c='b', label='Admitted')
ax.scatter(negetive['exam1'], negetive['exam2'], s=50, c='r', marker='x', label='Not Admitted')
# 设置图例显示在图的上方
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width , box.height* 0.8])
ax.legend(loc='center left', bbox_to_anchor=(0.2, 1.12),ncol=3)
# 设置横纵坐标名
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()


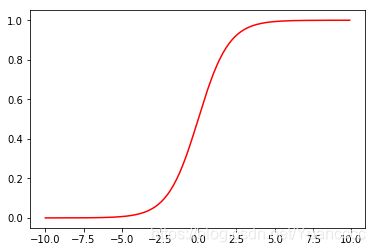
'''---------------------1.2 Sigmoid function-------------------'''

def sigmoid(z):
    return 1 / (1 + np.exp(- z))


x1 = np.arange(-10, 10, 0.1)
plt.plot(x1, sigmoid(x1), c='r')
plt.show()



'''---------------------1.3 Cost function---------------------'''


def cost(theta, X, y):
    first = (-y) * np.log(sigmoid(X @ theta))
    second = (1 - y)*np.log(1 - sigmoid(X @ theta))
    return np.mean(first - second)

#现在，我们要做一些设置，获取我们的训练集数据。
if 'Ones' not in data.columns:
    data.insert(0, 'Ones', 1)

# set X (training data) and y (target variable)
X = data.iloc[:, :-1].as_matrix()  # Convert the frame to its Numpy-array representation.
y = data.iloc[:, -1].as_matrix()  # Return is NOT a Numpy-matrix, rather, a Numpy-array.

theta = np.zeros(X.shape[1])


'''---------------------1.4 Gradient-----------------------'''

def gradient(theta, X, y):
    return (X.T @ (sigmoid(X @ theta) - y))/len(X) 

print(gradient(theta, X, y))# array([ -0.1, -12.00921659, -11.26284221])



'''---------------------1.5 Learning θ parameters---------------------'''

'''注意，我们实际上没有在这个函数中执行梯度下降，我们仅仅在计算梯度。在练习中，
一个称为“fminunc”的Octave函数是用来优化函数来计算成本和梯度参数。由于我们
使用Python，我们可以用SciPy的“optimize”命名空间来做同样的事情。

     这里我们使用的是高级优化算法，运行速度通常远远超过梯度下降。方便快捷。
只需传入cost函数，已经所求的变量theta，和梯度。cost函数定义变量时变量tehta
要放在第一个，若cost函数只返回cost，则设置fprime=gradient。'''

import scipy.optimize as opt

#这里使用fmin_tnc方法来拟合
result1=opt.fmin_tnc(func=cost,x0=theta,fprime=gradient,args=(X,y))
print(result1)
# (array([-25.16131867,   0.20623159,   0.20147149]), 36, 0)




#这里使用minimize方法来拟合，minimize中method可以选择不同的算法来计算，其中包括TNC
result2 = opt.minimize(fun=cost, x0=theta, args=(X, y), method='TNC', jac=gradient)
print(result2)

#fun: 0.2034977015894744
#     jac: array([9.11457705e-09, 9.59621025e-08, 4.84073722e-07])
# message: 'Local minimum reached (|pg| ~= 0)'
#    nfev: 36
#     nit: 17
#  status: 0
# success: True
#       x: array([-25.16131867,   0.20623159,   0.20147149])




print(cost(result1[0], X, y))
#0.2034977015894744



'''---------------------1.6 Evaluating logistic regression----------------------'''
'''学习好了参数θ后，我们来用这个模型预测某个学生是否能被录取。
接下来，我们需要编写一个函数，用我们所学的参数theta来为数据集X输出预测。
然后，我们可以使用这个函数来给我们的分类器的训练精度打分。
当hθ大于等于0.5时，预测 y=1
当hθ小于0.5时，预测 y=0 。'''

def predict(theta,X):
    probability=sigmoid(X@theta)
    return[1 if x>0.5 else 0 for x in probability]#return a list
    
final_theta=result1[0]
predictions=predict(final_theta,X)
correct=[1 if a==b else 0 for (a,b) in zip(predictions,y)]
accuracy=np.mean(correct)
print(accuracy)#0.89
#可以看到我们预测精度达到了89%，not bad.


#也可以用skearn中的方法来检验。
from sklearn.metrics import classification_report
print(classification_report(predictions,y))

#             precision    recall  f1-score   support

#         0       0.85      0.87      0.86        39
#         1       0.92      0.90      0.91        61

#avg / total      0.89      0.89      0.89       100



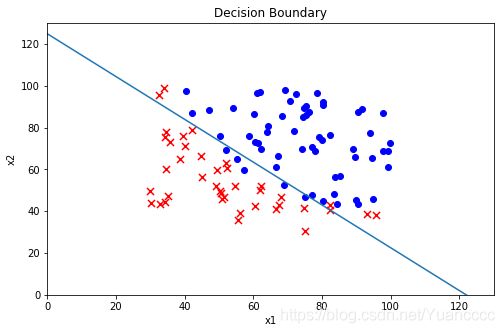
'''---------------------1.7 Decision boundary（决策边界）----------------------'''
'''在训练的第二部分，我们将要通过加入正则项提升逻辑回归算法。简而言之，正则化是成本函数
中的一个术语，它使算法更倾向于“更简单”的模型（在这种情况下，模型将更小的系数）。这个理论
助于减少过拟合，提高模型的泛化能力。这样，我们开始吧。
  设想你是工厂的生产主管，你有一些芯片在两次测试中的测试结果。对于这两次测试，你想决定是
否芯片要被接受或抛弃。为了帮助你做出艰难的决定，你拥有过去芯片的测试数据集，从其中你可
以构建一个逻辑回归模型。'''
#theta0+x1theta1+x2theta2=0
x1 = np.arange(130, step=0.1)
x2 = -(final_theta[0] + x1*final_theta[1]) / final_theta[2]

fig, ax = plt.subplots(figsize=(8,5))
ax.scatter(positive['exam1'], positive['exam2'], c='b', label='Admitted')
ax.scatter(negetive['exam1'], negetive['exam2'], s=50, c='r', marker='x', label='Not Admitted')
ax.plot(x1, x2)
ax.set_xlim(0, 130)
ax.set_ylim(0, 130)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_title('Decision Boundary')
plt.show()




'''====================2 Regularized logistic regression==================
    在训练的第二部分，我们将要通过加入正则项提升逻辑回归算法。简而言之，正则化是成本函
数中的一个术语，它使算法更倾向于“更简单”的模型（在这种情况下，模型将更小的系数）。这个
理论助于减少过拟合，提高模型的泛化能力。这样，我们开始吧。
    设想你是工厂的生产主管，你有一些芯片在两次测试中的测试结果。对于这两次测试，你想决
定是否芯片要被接受或抛弃。为了帮助你做出艰难的决定，你拥有过去芯片的测试数据集，从其中
你可以构建一个逻辑回归模型。'''

'''----------------------2.1 Visualizing the data-----------------------'''
data2 = pd.read_csv('ex2data2.txt', names=['Test 1', 'Test 2', 'Accepted'])

def plot_data():
    positive = data2[data2['Accepted'].isin([1])]
    negative = data2[data2['Accepted'].isin([0])]

    fig, ax = plt.subplots(figsize=(8,5))
    ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
    ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
    ax.legend()
    ax.set_xlabel('Test 1 Score')
    ax.set_ylabel('Test 2 Score')
    
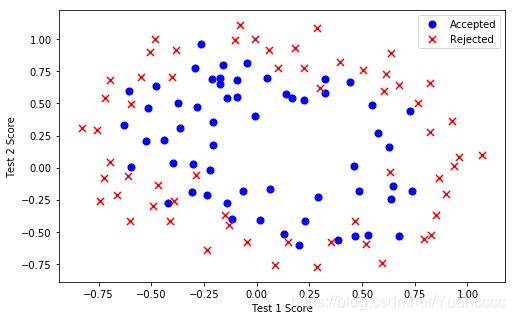
plot_data()	


'''注意到其中的正负两类数据并没有线性的决策界限。因此直接用logistic回归在这个数据集上
并不能表现良好，因为它只能用来寻找一个线性的决策边界。
所以接下会提到一个新的方法。'''
'''----------------------2.2 Feature mapping（特征映射）-------------------------'''

'''一个拟合数据的更好的方法是从每个数据点创建更多的特征。
我们将把这些特征映射到所有的x1和x2的多项式项上，直到第六次幂。
如果样本量多，逻辑回归问题很复杂，而原始特征只有x1,x2可以用多项式创建更多的特征
x1、x2、x1x2、x1^2、x2^2、... X1^nX2^n。因为更多的特征进行逻辑回归时，得到的
分割线可以是任意高阶函数的形状。'''

'''for i in 0..power
      for p in 0..i:
        output x1^(i-p) * x2^p'''
    



def feature_mapping(x1, x2, power):
    data = {}
    for i in np.arange(power + 1):
        for p in np.arange(i + 1):
            data["f{}{}".format(i - p, p)] = np.power(x1, i - p) * np.power(x2, p)

#     data = {"f{}{}".format(i - p, p): np.power(x1, i - p) * np.power(x2, p)
#                 for i in np.arange(power + 1)
#                 for p in np.arange(i + 1)
#             }
    return pd.DataFrame(data)


x1 = data2['Test 1'].as_matrix()
x2 = data2['Test 2'].as_matrix()

data3 = feature_mapping(x1, x2, power=6)
data3.head()


''' f00      f01       f02       f03       f04       f05       f06       f10  \
0  1.0  0.69956  0.489384  0.342354  0.239497  0.167542  0.117206  0.051267   
1  1.0  0.68494  0.469143  0.321335  0.220095  0.150752  0.103256 -0.092742   
2  1.0  0.69225  0.479210  0.331733  0.229642  0.158970  0.110047 -0.213710   
3  1.0  0.50219  0.252195  0.126650  0.063602  0.031940  0.016040 -0.375000   
4  1.0  0.46564  0.216821  0.100960  0.047011  0.021890  0.010193 -0.513250   

        f11       f12      ...            f30       f31       f32       f33  \
0  0.035864  0.025089      ...       0.000135  0.000094  0.000066  0.000046   
1 -0.063523 -0.043509      ...      -0.000798 -0.000546 -0.000374 -0.000256   
2 -0.147941 -0.102412      ...      -0.009761 -0.006757 -0.004677 -0.003238   
3 -0.188321 -0.094573      ...      -0.052734 -0.026483 -0.013299 -0.006679   
4 -0.238990 -0.111283      ...      -0.135203 -0.062956 -0.029315 -0.013650   

        f40       f41       f42           f50           f51           f60  
0  0.000007  0.000005  0.000003  3.541519e-07  2.477505e-07  1.815630e-08  
1  0.000074  0.000051  0.000035 -6.860919e-06 -4.699318e-06  6.362953e-07  
2  0.002086  0.001444  0.001000 -4.457837e-04 -3.085938e-04  9.526844e-05  
3  0.019775  0.009931  0.004987 -7.415771e-03 -3.724126e-03  2.780914e-03  
4  0.069393  0.032312  0.015046 -3.561597e-02 -1.658422e-02  1.827990e-02  

[5 rows x 28 columns]'''

'''经过映射，我们将有两个特征的向量转化成了一个28维的向量。
在这个高维特征向量上训练的logistic回归分类器将会有一个更复杂的决策边界，当我们在二维图
中绘制时，会出现非线性。
虽然特征映射允许我们构建一个更有表现力的分类器，但它也更容易过拟合。在接下来的练习中，
我们将实现正则化的logistic回归来拟合数据，并且可以看到正则化如何帮助解决过拟合的问题。'''


'''--------------------2.3 Regularized Cost function----------------------'''

'''正规损失函数方程
J(θ)= 1/m[i=1]∑[m][−y (i) log(hθ(x (i) ))−(1−y (i) )log(1−hθ(x(i)))]+λ/2m[j=1]∑[n]θj^2
​注意：不惩罚第一项θ0 
​先获取特征，标签以及参数theta，确保维度良好。'''
# 这里因为做特征映射的时候已经添加了偏置项，所以不用手动添加了。
X3=_data2.as_matrix()
y3=data2['Accepted'].as_matrix()
theta3=np.zeros(X3.shape[1])
X3.shape, y3.shape, theta3.shape  # ((118, 28), (118,), (28,))
 


def costReg(theta,X,y,l=1):
     #不惩罚第一项
     _theta=theta3[1:]
     reg=(l/(2*len(X)))*(_theta@_theta)
     return cost(theta,X,y)+reg
 
print(costReg(theta3,X3,y3,l=1))#0.69314718056


'''---------------------2.4 Regularized gradient-----------------------'''

'''对上面的算法中 j=1,2,…,n 时的更新式子进行调整可得：
θj:=θj(1−aλ/m)−a1/m[i=1]∑[m](hθ(x(i))−y(i))x(i)j '''

def gradientReg(theta,X,y,l=1):
    reg=(1/len(X))*theta
    reg[0]=0
    return gradient(theta,X,y)+reg

print(theta3,X3,y3,1)

'''---------------------2.5 Learning parameters-----------------------'''

result3 = opt.fmin_tnc(func=costReg, x0=theta3, fprime=gradientReg, args=(X3, y3, 2))
print(result3)


'''(array([ 1.27422005,  1.18590385, -1.41319107, -0.18067802, -1.2012929 ,
       -0.46790813, -0.93550853,  0.62478646, -0.91708239, -0.36458182,
       -0.27174441, -0.29276915, -0.13804215, -2.02173845, -0.36770528,
       -0.61999795, -0.27804409, -0.32917182,  0.12444362, -0.06288702,
       -0.05490418,  0.00961552, -1.465065  , -0.20901446, -0.29638538,
       -0.23663763,  0.02082839, -1.04396471]), 56, 4)'''


#我们还可以使用高级Python库scikit-learn来解决这个问题。

from sklearn import linear_model#调用sklearn的线性回归包
model=linear_model.LogisticRegression(penalty='l2',C=1.0)
print(model.fit(X3,y3.ravel()))

'''LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='warn',
          n_jobs=None, penalty='l2', random_state=None, solver='warn',
          tol=0.0001, verbose=0, warm_start=False)'''

print(model.score(X3,y3))#0.830508474576




'''----------------2.6 Evaluating logistic regression评估逻辑回归-------------------'''
final_theta3=result3[0]
predictions=predict(final_theta3,X3)
correct3=[1 if a==b else 0 for (a,b) in zip(predictions,y3)]
accuracy3=sum(correct3)/len(correct3)
print(accuracy3)     #0.8305084745762712


#或者用skearn中的方法来评估结果。

print(classification_report(y3,predictions))

'''           precision    recall  f1-score   support

           0       0.90      0.75      0.82        60
           1       0.78      0.91      0.84        58

   micro avg       0.83      0.83      0.83       118
   macro avg       0.84      0.83      0.83       118
weighted avg       0.84      0.83      0.83       118'''

#可以看到和skearn中的模型精确度差不多，这很不错。




'''----------------------2.6 Decision boundary（决策边界）------------------'''

#X×θ=0 (this is the line)

'''meshgrid函数将两个输入的数组x和y进行扩展，前一个的扩展与后一个有关，后一个的扩展
与前一个有关，前一个是竖向扩展，后一个是横向扩展。因为，y的大小为2，所以x竖向扩展
为原来的两倍，而x的大小为3，所以y横向扩展为原来的3倍。通过meshgrid函数之后，输入
由原来的数组变成了一个矩阵。通过使用meshgrid函数，可以产生一个表格矩阵。



无论contour还是contourf，都是绘制三维图，其中前两个参数x和y为两个等长一维数组，
第三个参数z为二维数组（表示平面点xi,yi映射的函数值）。'''


x4=np.linspace(-1,1.5,250)
xx,yy=np.meshgrid(x4,x4)#通过使用meshgrid函数，可以产生一个表格矩阵。

z=feature_mapping(xx.ravel(),yy.ravel(),6).as_matrix()
z=z@final_theta3
z=z.reshape(xx.shape)#xx.shape  250*250

plot_data()
plt.contour(xx,yy,z,0)
plt.ylim(-.8,1.2)

画图结果：