卡尔曼滤波在Webrtc中应用的理解

卡尔曼滤波在webrtc中有多处运用，这里简单总结一下自己的一些认识。

1.卡尔曼滤波的理解

本节主要记录自己对卡尔曼滤波中，哪些量代表啥，哪些量是需要根据系统性质设置，哪些量需要手动调，分别如何影响输出的总结。

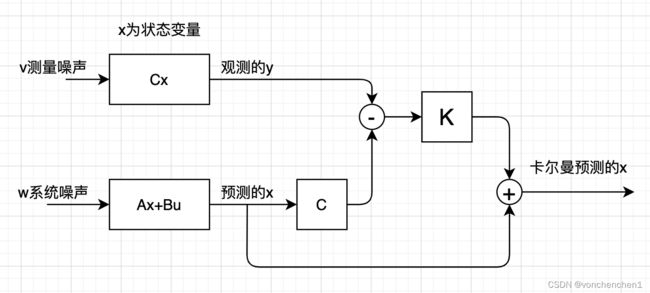
上图描述了卡尔曼滤波的基本流程，对于一些系统无法直接预测到他下一次的输出，但是可以通过间接测量得到一些信息，同时我们也知道本身系统的一些特点，基于这两者通过卡尔曼滤波，预测出系统的输出。

上面框框中会输出一个yk，这个相当于观测器观测到的数据，实际应用我理解就是传感器检测到的值，xk是我们想知道的真的输出量(卡尔曼最终就是要猜出xk的值)，对于上面的框框，我们只能得到y的值。A代表了这个系统，B是施加的外部控制量，C代表了我们要猜测的xk与输出yk的关系，注意我们现在只能得到yk的值，通过C是xk与yk的转换关系，wk是系统的噪声，vk是观测噪声。

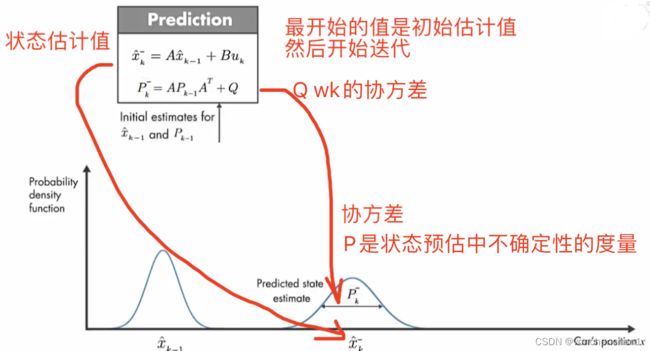
下面的框框是我们知道模型后，对输出xk做出的预测，这个预测没有当前的系统噪声和测量噪声。这样我们得到的估计值可能是不准确的，如途中xk尖。通过对估计的xk尖的观测，可以得到一个y尖。下面就比较观测值的差距，经过处理，反馈给下一次的估计，从而修正下一次估计的x尖，同样下一次也会观测当前的x尖，得到新的y尖，再与系统数据的y尖比较，反馈给下下此输入用于修正x尖。上图中，xk尖是预测的，他的不确定性会增加，所以方差比较大，看起来比较胖。棕色的yk是测量量，他也有误差，也是一个分布。

这个反馈修正过程的描述就是下面的式子，预测值与反馈值合起来，得到当前最优估计值。

 

 

 

要看一下K是怎么求的

参数解释

wk 在建模过程中模型与真实系统的误差( Ax+Bu 对系统化简导致的误差 为系统噪声)

R是测量误差vk的方差    测量准确R小

Q是系统噪声wk的方差  模型准确Q小   

P估计误差的协方差，Q、R、C参与计算得出P

这两个值可以调节，用来表示当前观测的准确程度和系统的噪声程度，传感器越准确，观测噪声越小，R可以调小，相信传感器的多。当前系统噪声越大，系统波动范围大，Q也就需要大些，相信上次预测的程度减小。最终目的是让P减小，通过K的不断调整，让P越来越小，状态预估不确定性降低，结果越来越准确。

A，B，C都是系统属性决定的。

R:我们观测到的每个数据，可以认为其对应某个真实的状态。但是因为存在不确定性，某些状态的可能性比另外一些可能性更高。我们将这种不确定性的方差为描述为Rk

 

模型也不准，观测也不准，那么该信谁，互相取多少作为最终占比呢。

 2.一维例子

 下面简单写了一个一维卡尔曼滤波的例子，用于直观上理解卡尔曼滤波。这里自己生产一个离散的正弦信号，然后给这个正弦信号叠加噪声，得到一个噪声信号。这个噪声新号就是我们的观测值，signal_x相当于我们给出的系统模型的输出，这里直接给A*上一次的输出，作为系统的预测输出，通过调节测量误差R和系统误差Q，观察输出与真实正弦信号的差别。

# -*- coding: utf-8 -*-

import matplotlib.pyplot as plt
import numpy as np

NUM = 10240
signal_std = [0]*NUM

signal_y_noise = 0.1*np.random.randn(NUM) #观测噪声
signal_y = [0]*NUM
signal_x = [0]*NUM
noise_system = 0.01*np.random.randn(NUM) #模拟系统输出的一些噪声，Q应该不止是这段噪声的方差

A = 1 #系统矩阵 假定就是1 预计输出信号和输入一致
B = 0 #控制矩阵

C = 1 #观测矩阵

#造一段加了系统噪声和观测噪声的传感器输出值
for i in range(1, NUM):
    signal_std[i] = np.sin(0.01*i) #A=1和sin相差很多
    #signal_std[i] = 1-np.exp(-0.05*i) #模拟电容充电 
    signal_y[i] = C*(A*signal_std[i] + noise_system[i])+ signal_y_noise[i]

#R Q 可以调节
#R测量误差 vk 的协方差矩阵 目前vk是我们自己造的signal_y_noise 可以直接求出R 
#R = np.var(signal_y_noise)  #这个值越大 越不相信测量值
R = 0.6 
#Q系统噪声 wk 的协方差矩阵 目前wk是我们自己造的noise_system 可以直接求出  包括过程噪声，系统与真实的误差？
#目前看Q小 预测曲线越平滑，跟踪效果越差
#Q = np.var(noise_system)
Q = 0.01
#Q = 0

print("R=%10.10f"%R)
print("Q=%10.10f"%Q)

P = [0]*NUM
P[0] = 1 #系统A目前就是系数1 协方差比较大

K = 0

for i in range(1, NUM):
    #预测  
    signal_x[i] = A*signal_x[i-1] #(B*u[i])
    P[i] = P[i-1] + Q

    #更新
    K = P[i] / (P[i] + R)
    #当前最优估计  预测+K*(真实观测值 - 预测值的观测值)
    signal_x[i] = signal_x[i] + K*(signal_y[i]-C*signal_x[i])
    P[i] = (1 - K*C)*P[i] 

    if (i<20) or i%100 == 0 :
        print("P[%d]=%10.10f K=%10.10f"%(i,R,K))
    
plt.plot(signal_y,color = 'g',label = 'measure') 
plt.plot(signal_std,color = 'r',label = 'origin')    
plt.plot(signal_x,color = 'b',label = 'filter') 
plt.legend(bbox_to_anchor=(0.7, 0.05), loc=3, borderaxespad=0)

plt.show()

关于Q的疑问

系统中系统误差w指什么，这里我理解这个w指的是系统模型和真实模式间的差距，Q是这个w的协方差矩阵。

Q=0

如果给出的模型与真正的系统差别太大，说明系统误差w很大，Q应该调的比较大，如果这个时候Q为0，完全相信模型的估计值，那么观测值所占的比重越来越小，最后输出的预测值完全跟着模型走了。

3.webrtc中timestamp_extrapolator 到达时间估计 

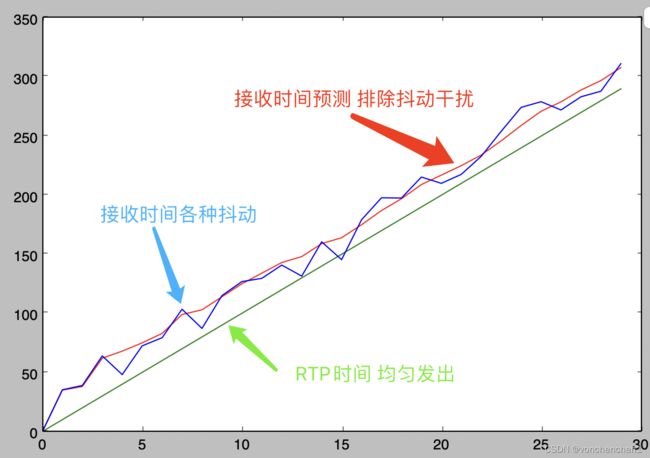
这里单独抽出了timestamp_extrapolator.cc类中相关代码，单独编译为动态库。使用Python脚本模拟接收rtp包时间不均。根据rtp时间和收到时间，预测下一个帧的到达时间。可以看到下图，经过卡尔曼预测出的红线逐渐稳定并与RTP发送时间基本平行。

这里卡尔曼每次需要预测两个值，第一个值是对于要预测的帧，他的第一个其实时间，第二个值是经过抖动后这个视频rtp与真实毫秒时间的关系可能不再是90，而是根据卡尔曼预测收敛出的一个值。注意这个代码中Q矩阵是0，最终相信预测值。

下面的流程直接套用卡尔曼公式

1.初始化x   

    //w相当于x

    // C = [当前收到的时间,1]'

    // C' = [当前收到的时间,1]

    // 估计的接收的时间 [当前收到的时间,1]*[_w[0], _w[1]]'

    _w[0] = 90.0; //用于估计rtp时间戳与毫秒时间戳的倍数(正常为90 卡尔曼预测下次到达时可能会调整)

    _w[1] = 0;    用于估计起始时间

2.更新卡尔曼参数，这里lambda可以调节，程序默认给出经验值。   

 //C = [t(k) 1]'; //这个就是C

    //C' = [t(k) 1]

    //that = C'*w;  t(k)*w[0] + w[1] 这里w[1]的正负号好像是反的

    //K = P逆*C转置/(lambda + C'*P*C);  这里lambda相当于R 测量噪声，这里是1

    double K[2];

    K[0] = _pP[0][0] * tMs + _pP[0][1];

    K[1] = _pP[1][0] * tMs + _pP[1][1];

    double TPT = _lambda + tMs * K[0] + K[1];

    K[0] /= TPT;

    K[1] /= TPT;



    

    //更新预测量w 更新90khz对应的值 更新起始时间对应值

    //residual 相当于 (yk - Cxk)

    //使用卡尔曼系数 更新上一次的x，得到最优估计

    //最终让这个最优x通过观测矩阵C 得到当前估计时间



    //_w原始值 与 卡尔曼系数*差值，一边相信一点，得出新的_w。由于这里Q为0，根据上一节的结论，很可能认为这里最终还是相信

    //90khz以及发出时间的，而这两个值本身也是准确的，但是由于网络抖动的影响所以一开始会加入观测值。(这句话是我感觉的，不确定对不对)



    //w = w + K*(ts(k) - that);

    _w[0] = _w[0] + K[0] * residual;

    _w[1] = _w[1] + K[1] * residual;



    //P = 1/lambda*(P - K*T'*P);

    //P = (I - K*C)*P

    double p00 = 1 / _lambda *

                 (_pP[0][0] - (K[0] * tMs * _pP[0][0] + K[0] * _pP[1][0]));

    double p01 = 1 / _lambda *

                 (_pP[0][1] - (K[0] * tMs * _pP[0][1] + K[0] * _pP[1][1]));

    _pP[1][0] = 1 / _lambda *

                (_pP[1][0] - (K[1] * tMs * _pP[0][0] + K[1] * _pP[1][0]));

    _pP[1][1] = 1 / _lambda *

                (_pP[1][1] - (K[1] * tMs * _pP[0][1] + K[1] * _pP[1][1]));

    _pP[0][0] = p00;

    _pP[0][1] = p01;

下面是制造噪声并调用动态库测试的代码

# -*- coding: utf-8 -*-

import matplotlib.pyplot as plt
import numpy as np

from ctypes import *

#kalman_library = cdll.LoadLibrary("./build/libkalman_webrtc.dylib")
#mac下用绝对路径调
kalman_library = cdll.LoadLibrary("你的路径/kalman/webrtc/build/libkalman_webrtc.dylib")

NUM = 30
#模拟均匀采集的RTP时间戳
rtp_ts = [0]*NUM
#模拟经过网络传输接收到的RTP包的接收时间
receive_ts = [0]*NUM
#制造抖动
jitter_ts = 10*np.random.randn(NUM)

#网络延迟
network_delay = 20

predicted_receive_ts = [0]*NUM

for i in range(1, NUM):
    #模拟rtp均匀发出 10ms
    rtp_ts[i] = i*10 * 90

    receive_ts[i] = i*10 + network_delay + jitter_ts[i]

    #卡尔曼预测到达时间
    predicted_receive_ts[i] = kalman_library.kalman_timestamp_extrapolator(int(receive_ts[i]), int(rtp_ts[i]))
    #predicted_receive_ts[i] = kalman_library.kalman_timestamp_extrapolator(2, 2)

#为了显示
for i in range(1, NUM):
    rtp_ts[i] = rtp_ts[i] / 90
    
plt.plot(rtp_ts,color = 'g',label = 'rtp时间') 
plt.plot(predicted_receive_ts,color = 'r',label = '卡尔曼预测到达时间')    
plt.plot(receive_ts, color = 'b',label = '观测的到达时间') 

plt.show()

4.webrtc中jitter delay 抖动估计  

 这里的实验还是单独抽取webrtc代码jitter_estimator.cc，编译为动态库，使用Python脚本制造数据并调用这个动态库进行测试。

如下图所示，蓝色线代表当前来的帧的大小，绿线代表每帧完整到达的时间，红色是卡尔曼估计的jitter时间，最终播放的延迟会在这个jitter时间上做一些修正然后提供给控制交给渲染的定时器。

由于大帧的存在以及当前一段时间网络的延迟情况，如果来一帧直接播放一帧，那么就会像绿线一样的折点一样(反应了每帧的到达时间)，会忽快忽慢的播放，这样导致有些帧显示时间极短，有些帧显示时间极长最终影响到视频观看的效果。这样需要一个延迟时间，能根据当前一段时间的网络情况以及包大小估计一个延迟时间，不管比较大的关键帧来了还是比较小的非关键帧都能比较稳定的播放。

可以看到刚开始的时候红线不是稳定的，遇到大帧的时候会突然增大，然后会减小，反复4次左右后红线趋于稳定。相当于卡尔曼滤波在迭代的过程中估计误差Q逐步收敛。

最终 jitter估计时间 -> [(大帧长度-平均帧长)/当前传输速率] + rtt修正传输噪声  共同估计出当前jitter时间。

卡尔曼预测在这里做的操作就是要把当前传输速率通过当前 到达间隔的时间差 与帧大小预测出来。其中时间差是观测值，帧大小通过卡尔曼预测的参数经过转换可以得出一个时间差，卡尔曼预测在这里做的事情就是将预测值与真实值逐渐变的接近。

代码流程

4.1.输入

参数1  jitter时间  frameDelayMS = (receive_ts[i] - receive_ts[i-1]) - (receive_ts[i-1] - receive_ts[i-2])

参数2  当前帧的大小

4.2.VCMJitterEstimator::UpdateEstimate 更新卡尔曼参数

 1.当前帧大小与之前 _varFrameSize 滑动平均，得到新的_varFrameSize平均帧大小

2.更新噪声，用当前卡尔曼估计的jitter时间与实际jitter时间之差计算噪声，最终代表网络延迟加入用于修正jitter时间估计

	   double deviation = DeviationFromExpectedDelay(frameDelayMS, deltaFS);
	   //这里deviation = frameDelayMS - (_theta[0] * deltaFSBytes + _theta[1]);  代表了当前的jitter时间与用上一次卡尔曼参数	   与当前平局帧大小计算的估计jitter时间做差，用于计算网络中噪声影响。
	
	   //deviation小于一定阈值或者帧大小大于一定阈值后要噪声
	   EstimateRandomJitter(deviation, incompleteFrame, now);
		   
	   //当前真实jitter时间与当前帧大小差通过卡尔曼预测再观测出来的jitter时间 alpha计算是什么原理 越靠近现在的权重越大?
           double avgNoise = alpha * _avgNoise + (1 - alpha) * d_dT;
   	   //d_dT噪声方差
  	   double varNoise =  alpha * _varNoise + (1 - alpha) * (d_dT - _avgNoise) * (d_dT - _avgNoise);
  	   if (!incompleteFrame || varNoise > _varNoise) {
           	_avgNoise = avgNoise;
    		_varNoise = varNoise;
  	    }

4.3.更新卡尔曼系数

最终jitter估计时间 -> [(大帧长度-平均帧长)/当前传输速率] + rtt修正传输噪声  共同估计出当前jitter时间这一步 frameDelayMS - (deltaFSBytes * _theta[0] + _theta[1]);

_theta[0]是  1/当前传输速率，_theta[1]是网络延迟，通过迭代更新这俩值，得出jitter时间的前半部分。后半部分由步骤2得出的结论根据rtt进一步修正。注意_theta[1]代表网络延迟，最终计算jitter时间的时候，这部分是不参与计算的，这里使用主要是需要根据当前实际jitter时间计算误差，属于卡尔曼公式的一部分

1. 前后两帧大小差deltaFS大到一定程度 (deltaFS) > - 0.25 * _maxFrameSize 更新卡尔曼参数。因为大到一定程度后可能之前的卡尔曼系数不准确了，需要推倒重新获取。

2.KalmanEstimateChannel(frameDelayMS, deltaFS);

// 时间差frameDelayMS(第2帧发送到接收时间 - 第1帧发送到接收时间)  数据大小差deltaFSBytes(C 观测矩阵用这个)
		// 传递变化deltaFSBytes导致时间变化frameDelayMS
		VCMJitterEstimator::KalmanEstimateChannel(int64_t frameDelayMS,  int32_t deltaFSBytes)
			
	
			//_thetaCov相当于P矩阵  P(Q噪声我理解是与实际系统误差的方差)
    // Prediction
    // M = M + Q
    _thetaCov[0][0] += _Qcov[0][0];
    _thetaCov[0][1] += _Qcov[0][1];
    _thetaCov[1][0] += _Qcov[1][0];
    _thetaCov[1][1] += _Qcov[1][1];

    // 注意这里_thetaCov(P矩阵)的排列是下面这样 可以理解为每个向量是竖着，而不是数组每行横着
    // _thetaCov[0][0]  _thetaCov[1][0]
    // _thetaCov[0][1]  _thetaCov[1][1]

    // Kalman gain
    // K = M*h'/(sigma2n + h*M*h') = M*h'/(1 + h*M*h')
    // h = [dFS 1]
    // Mh = M*h'
    // hMh_sigma = h*M*h' + R

    //卡尔曼系数分子 P逆*C转置   C->[deltaFSBytes, 1]  
    Mh[0] = _thetaCov[0][0] * deltaFSBytes + _thetaCov[0][1];
    Mh[1] = _thetaCov[1][0] * deltaFSBytes + _thetaCov[1][1];
    // sigma weights measurements with a small deltaFS as noisy and
    // measurements with large deltaFS as good
    if (_maxFrameSize < 1.0)
    {
        return;
    }
    //计算测量误差R 为什么这样计算有待考证
    double sigma = (300.0 * exp(-fabs(static_cast(deltaFSBytes)) /
                   (1e0 * _maxFrameSize)) + 1) * sqrt(_varNoise);
    if (sigma < 1.0)
    {
        sigma = 1.0;
    }

    //卡尔曼系数分母  分子中已经计算好了 P逆*C转置 也就是[Mh[0], Mh[1]]' 
    //C*P逆*C转置 ->  [deltaFSBytes, 1] * [Mh[0], Mh[1]]' 
    //sigma 是测量噪声R
    hMh_sigma = deltaFSBytes * Mh[0] + Mh[1] + sigma;
    if ((hMh_sigma < 1e-9 && hMh_sigma >= 0) || (hMh_sigma > -1e-9 && hMh_sigma <= 0))
    {
        assert(false);
        return;
    }
    //计算出卡尔曼系数
    kalmanGain[0] = Mh[0] / hMh_sigma;
    kalmanGain[1] = Mh[1] / hMh_sigma;

    //
    // Correction
    // theta = theta + K*(dT - h*theta)
    // yk - C*(x的预测值) ->  frameDelayMS - [deltaFSBytes, 1]* [_theta[0], _theta[1]]'
    // measureRes 得出输出与估计输出的差    frameDelayMS输入的帧延迟
    // frameDelayMS真实延迟变化  -  ((deltaFSBytes真实收到数据变化/估计传输时间_theta[0])+  当前网络导致的延迟_theta[1]) 
    // 也就是说  帧延迟时间变化 = 数据大小变化 + 当前网络延迟
    measureRes = frameDelayMS - (deltaFSBytes * _theta[0] + _theta[1]);
    //更新x矩阵    [deltaFSBytes, 1]* [_theta[0], _theta[1]]' -> 相当于估计得到的当前输出
    _theta[0] += kalmanGain[0] * measureRes;
    _theta[1] += kalmanGain[1] * measureRes;
    //1/_theta[0] 为估计的当前传输速率

    //最终 (大帧长度-平均帧长)/当前传输速率 + rtt修正传输噪声  共同估计出当前jitter时间
    //其中传输噪声由 frameDelayMS - (_theta[0] * deltaFSBytes + _theta[1]) 也就是真实delay与卡尔曼估计的delay的差距决定
    // GetJitterEstimate(rtt)

    if (_theta[0] < _thetaLow)
    {
        _theta[0] = _thetaLow;
    }

    // 更新P矩阵
    // M = (I - K*h)*M
    t00 = _thetaCov[0][0];
    t01 = _thetaCov[0][1];
    _thetaCov[0][0] = (1 - kalmanGain[0] * deltaFSBytes) * t00 -
                      kalmanGain[0] * _thetaCov[1][0];
    _thetaCov[0][1] = (1 - kalmanGain[0] * deltaFSBytes) * t01 -
                      kalmanGain[0] * _thetaCov[1][1];
    _thetaCov[1][0] = _thetaCov[1][0] * (1 - kalmanGain[1]) -
                      kalmanGain[1] * deltaFSBytes * t00;
    _thetaCov[1][1] = _thetaCov[1][1] * (1 - kalmanGain[1]) -
                      kalmanGain[1] * deltaFSBytes * t01;

4.4.获取预测的jitter delay

1.int VCMJitterEstimator::GetJitterEstimate(double rttMultiplier)

ret = _theta[0] * (_maxFrameSize - _avgFrameSize) + NoiseThreshold();

使用平均帧大小计算一下当前由帧大小造成的网络抖动，再加上当前网络噪声，得到一个预测值

2.根据平均帧率对预测值进行修正并返回

下面是Python测试代码

# -*- coding: utf-8 -*-

import matplotlib.pyplot as plt
import numpy as np
import random

from ctypes import *

#kalman_library = cdll.LoadLibrary("./build/libkalman_webrtc.dylib")
#mac下用绝对路径调
kalman_library = cdll.LoadLibrary("你的路径/kalman/webrtc/build/libkalman_webrtc.dylib")

NUM = 256
#模拟均匀采集的RTP时间戳
rtp_ts = [0]*NUM
#模拟经过网络传输接收到的RTP包的接收时间
receive_ts = [0]*NUM
#制造抖动
jitter_ts = 9*np.random.randn(NUM)

#模拟帧大小序列
frame_bytes = [0]*NUM
base_frame_bytes = 100
for i in range(1, NUM):
    if(i%15 == 0):
        #模拟一个关键帧大小 比别的帧大
        frame_bytes[i] = base_frame_bytes*10 + (base_frame_bytes/5)*random.uniform(0,2)
        #print('lidechen %d'%frame_bytes[i])
    else :
        frame_bytes[i] = base_frame_bytes + (base_frame_bytes/5)*np.random.uniform(0,1)

#记录真实jitter
real_jitter_array = [0]*NUM
#记录真实每帧传输时间
real_trans_spend_array = [0]*NUM

#网络延迟
network_delay = 20

kalman_jitter = [0]*NUM

for i in range(1, NUM):
    #模拟rtp均匀发出 33.3ms
    rtp_ts[i] = i*33.3333 * 90

    #增加网络延迟与抖动
    receive_ts[i] = i*33.3333 + network_delay + jitter_ts[i]
    if(i%15 == 0):
        #遇到关键帧延迟增大 
        receive_ts[i] += (5+ random.randint(0,9))

    if(i>=3):
        if(receive_ts[i] < receive_ts[i-1]):
            #防止造的接收时间出错，后面的时间必须大于前面的
            receive_ts[i] = receive_ts[i-1] + 1        

        #卡尔曼预测到达时间
        #kalman_jitter_estimator(int frameDelayMS, int frameSizeBytes, long now, double rttMultiplier);
        frameDelayMS = (receive_ts[i] - receive_ts[i-1]) - (receive_ts[i-1] - receive_ts[i-2])
        real_jitter_array[i] = frameDelayMS
        real_trans_spend_array[i] = receive_ts[i] - receive_ts[i-1]

        frameSizeBytes = frame_bytes[i]
        #假设从0开始计时 输入抖动时间frameDelayMS 以及当前凑齐包的完整帧的大小，估计当前帧啥时候播放
        now = receive_ts[i]
        kalman_jitter[i] = kalman_library.kalman_jitter_estimator(int(frameDelayMS), int(frameSizeBytes), int(now))

#为了显示 rtp时间戳转换为毫秒
for i in range(1, NUM):
    rtp_ts[i] = rtp_ts[i] / 90
    
plt.plot(kalman_jitter,color = 'r',label = '卡尔曼预测jitter')    
#plt.plot(real_jitter_array, color = 'b',label = 'jitter') 
plt.plot(real_trans_spend_array, color = 'g',label = '每帧接收间隔时间') 

for i in range(1, NUM):
    frame_bytes[i] = frame_bytes[i] / 10

plt.plot(frame_bytes, color = 'b',label = '每帧接收间隔时间') 

plt.show()