（sklearn学习笔记）逻辑回归

逻辑回归的基础一线性回归简介

线性回归公式：

写成矩阵形式：

其中：

• θ：模型的参数
• θ0：截距
• θ1-θn：系数

线性回归的任务：构造预测函数z来映射输入的特征矩阵x和标签值y的线性关系；

注：通过函数z，线性回归使用输入的特征矩阵X来输出一组连续型的标签值y_pred，以完成各种预测连续型变量的任务（比如预测产品销量，预测股价等等）。

线性回归的核心：找出模型的参数θ，最著名的方法是最小二乘法。

逻辑回归一预测离散型标签

联系函数：将连续型变量转化为离散型变量的函数。

标签为0-1的离散型变量，二分类思想

Sigmoid函数

• S型函数；
• 当z→∞时，g(z)→1；当z→-∞时，g(z)→0；
• 用于将任何实数映射到(0,1)区间，使其可用于将任意值函数转换为更适合二分类的函数;
• 归一化的方法，同理的还有MinMaxSclaer方法，只不过它将函数转化到[0,1]区间而不是(0,1)。

二元逻辑回归的一般形式

y(x)∈(0，1)，y(x)+(1-y(x))=1；

形似几率y(x)/(1-y(x))取对数得:

形似几率取对数的本质是线性回归z，因此逻辑回归又叫"对数几率回归"。

---

y(x)：本质上不是概率，却拥有着概率的性质，因此被当作概率来使用。

y(x)与1-y(x)：可以看成一对正反例，y(x)是某样本标签被预测为1的概率，1-y(x)是某样本标签被预测为0的概率，y(x)/(1-y(x))是样本i的标签被预测为1的相对概率。

注：使用最大似然法和概率分布函数推导出逻辑回归的损失函数，并且把返回样本在标签取值上的概率当成是逻辑回归的性质来使用，每当我们诉求概率的时候，我们都会使用逻辑回归。

逻辑回归除了可以用来二分类，也可以多分类

逻辑回归的优势

• 对线性关系的拟合效果极好；
• 计算快；
• 返回的分类结果不是固定的0，1，而是以小数形式呈现的类概率数字；
  注：决策树，随机森林等输出的是分类结果，但不会计算分数。
• 抗噪能力强：技术上来说，最佳模型的AUC面积低于0.8时，逻辑回归明显优于树模型”的说法。并且，逻辑回归在小数据集上表现更好，在大型的数据集上，树模型有着更好的表现。

逻辑回归的数学目的

求解能够让模型对数据拟合程度最高的参数θ的值，以此构建预测函数y(x)，然后将特征矩阵X输入预测函数来计算出逻辑回归的结果y。

sklearn种最简单的逻辑回归分类器

（又叫logit回归，最大熵分类器）

class  sklearn.linear_model.LogisticRegression (penalty=’l2’, dual=False, tol=0.0001, C=1.0,
fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=’warn’, max_iter=100,
multi_class=’warn’, verbose=0, warm_start=False, n_jobs=None)

可能会用到的其它类

• metrics.confusion_matrix一混淆矩阵，模型评估指标之一
• metrics.roc_auc_score一ROC曲线，模型评估指标之一
• metrics.accuracy_score一精确性（最常用），模型评估指标之一

二元逻辑回归的损失函数

两种模型表现：

• 在训练集上的模型表现
• 在测试集上的模型表现

逻辑回归与决策树及随机森林的区别：

• 逻辑回归侧重于追求模型在训练集上表现最优；
• 决策树及随机森林侧重于追求模型在测试集上表现最优。

---

损失函数一衡量参数θ优劣的评估指标，求解最优参数的工具

• 损失函数小，模型在训练集上表现优异，拟合充分，参数优秀；
• 损失函数大，模型在训练集上表现差劲，拟合不足，参数糟糕

注：没有"求解参数"需求的模型没有损失函数，eg：KNN，决策树。

损失函数由极大似然估计推导出：

其中：

• θ：求解出来的参数
• m：样本的个数
• yi：样本i真实的标签
• yθ(xi):样本i基于θ预测的标签值
• xi：样本i的各个特征的值

逻辑回归追求：能够让J(θ)取min的参数组合；

注：对于J(θ)，x、y是已知参数，θ是自变量，求导(或偏导)时要注意对θ求导(或偏导)。

损失函数的数学推导

将两种概率整合得：

（模型拟合好，损失小的目的，我们每时每刻都希望 的值等于1）

概率：

取对数得：

取负值：

（在这个函数上，追求最小值就能让模型在训练数据上的拟合效果最好，损失最低）

LogisticRegression常用重要参数、属性及接口

正则化

（因为极力追求J(θ)的最小值，让模型在训练集上表现最有，但是在测试集上表现却不好，即出现了过拟合的现象，为了对逻辑回归中的过拟合进行控制，可以正则化。）

1. LogisticRegression种最常用的正则化方法：

• L1正则化：J(θ)+θ的L1范式的倍数；
• L2正则化：J(θ)+θ的L2范式的倍数；

（正则项/惩罚项：即J(θ)后加的范式）

其中，

• C：控制正则化程度的超参数，在LogisticRegression中参数的名字也是C；
• n：方程中特征的总数；
• j≥1的原因：因为θ中的第一个参数θ0是截距，一般不参与正则化。

2. 正则化调节模型拟合程度的方法：正则化后，损失函数改变，基于损失函数的最优化求得的解θ就会随之改变。
3. 一些其他博客或资料中，正则化后的损失函数也会这样写：
   
   但在sklearn中，常数C通常写在J(θ)的前面，通过调节J(θ)的大小，来调节对模型的惩罚。
4. L1/L2正则化效果不同：正则化强度越大，C越小，θ越的取值越小

• L1正则化可以将参数θ中的元素压缩到0；

  (在L1正则化的过程中，携带信息量小的、对模型贡献不大的特征的参数会比携带信息量大的、对模型贡献大的特征的参数更快地变为0，因为L1正则化其实是一个特征选择的过程，掌管了参数的"稀疏性"。L1正则化也正是基于此来防止过拟合，由于L1正则化这个性质，逻辑回归的特征选择可以由embedded嵌入法来完成。)

• L2正则化不会将参数θ中的元素压缩到0，但是会让元素变得非常小（趋于0）。

• 由此可以看出，L1正则化的效力更大，因此，如果数据维度很高，特征量很大，我们倾向于使用L1正则化。

• 如果我们得目的只是简单的正则化防止过拟合，那么用L2就够了，如果L2后还是过拟合或者是在数据集上的表现很差，那就使用L1。

参数penalty

指定正则化的方式，默认为"l2"，有以下两种取值：

• l1：即L1正则化，参数solver只能取"saga"和"liblinear"；
• l2：即L2正则化，参数solver可以取任意值。

参数C

正则化强度的倒数，一个大于0的浮点数，默认1.0，即正则项与损失函数的比例是1：1；

• C越小，损失函数越小，模型对损失函数的惩罚越重，正则化效力越强，θ会被压缩得越来越小；
• 两种正则化方法下的C值如果没法确定的话，可以使用学习曲线来寻找最优的C值。

属性coef_

查看每个特征对应的参数，可以在正则化前后分别调用该属性来清晰地看到正则化的效果。

例子

lrl1=LR(penalty="l1",solver="liblinear",C=0.5,max_iter=1000)
lrl2=LR(penalty="l2",solver="liblinear",C=0.5,max_iter=1000)
lrl1=lrl1.fit(x,y)  #x,y 分别是特征矩阵和标签
lrl1.coef_ 

array([[ 4.00036718,  0.03179879, -0.13708193, -0.01622688,  0.        ,
         0.        ,  0.        ,  0.        ,  0.        ,  0.        ,
         0.        ,  0.50444988,  0.        , -0.07126651,  0.        ,
         0.        ,  0.        ,  0.        ,  0.        ,  0.        ,
         0.        , -0.24568087, -0.12857603, -0.01440636,  0.        ,
         0.        , -2.04168215,  0.        ,  0.        ,  0.        ]])

lrl2=lrl2.fit(x,y)
lrl2.coef_

array([[ 1.61358623e+00,  1.00284781e-01,  4.61036191e-02,
        -4.21333984e-03, -9.27388895e-02, -3.00561176e-01,
        -4.53477303e-01, -2.19973055e-01, -1.33257382e-01,
        -1.92654788e-02,  1.87887747e-02,  8.75532438e-01,
         1.31708341e-01, -9.53440922e-02, -9.64408195e-03,
        -2.52457845e-02, -5.83085040e-02, -2.67948347e-02,
        -2.74103894e-02, -6.09326731e-05,  1.28405755e+00,
        -3.00219699e-01, -1.74217870e-01, -2.23449384e-02,
        -1.70489339e-01, -8.77400140e-01, -1.15869741e+00,
        -4.22909464e-01, -4.12968162e-01, -8.66604813e-02]])

l1=[]
l2=[]
l1test=[]
l2test=[]
Xtrain,Xtest,Ytrain,Ytest=train_test_split(x,y,test_size=0.3,random_state=420)
for i in np.linspace(0.05,1,19):
    lrl1 = LR(penalty="l1",solver="liblinear",C=i,max_iter=1000)
    lrl2 = LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)
    lrl1 = lrl1.fit(Xtrain,Ytrain)
    #用accuracy_score进行打分，来评价预测的效果
    l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain))
    l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))

    lrl2 = lrl2.fit(Xtrain,Ytrain)
    l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
    l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
    
#画曲线来直观得显示预测的效果
graph=[l1,l2,l1test,l2test]
color=["green","black","lightgreen","gray"]
label=["L1","L2","L1test","L2test"]
plt.figure(figsize=(6,6))
for i in range(len(graph)):
    plt.plot(np.linspace(0.05,1,19),graph[i],color[i],label=label[i])
plt.legend(loc=4) #图例的位置在哪里?4表示，右下角
plt.show()        #由图判断出，当C等于0.8或0.9左右时，四个拟合效果都是好的；若C更大，会表现出过拟合的现象

特征工程

1. 业务选择：一个人可以通过很多个特征来进行判别不如使用几个特征来判别的方便。

• 如果熟悉业务，可以自己选择重要的特征；
• 如果不熟悉业务，或特征数量巨大，那么就可以借助算法，筛选过一遍后再根据常识选择出重要的特征。

2. PCA和SVD一般不用

• PCA和SVD是高效降维算法，但是其降维后具有不可解释性，所以不用；
• 希望逻辑回归的结果能够保留原特征。

3. 可以使用统计方法，但是没有必要

• 逻辑回归的要求低于线性回归，不需要了解数据的总体分布和方差，也不需要排除特征间的多重共线性，但使用卡方、方差、互信息等统计方法来特征选择也可以，过滤法中的所有方法都可以用在逻辑回归中。
• 多重共线性对线性回归的影响比较大，所以我们必须使用方差膨胀因子VIF来消除共线性；但对于逻辑回归来说不一定有用，有时我们还需要根据一些相关连的特征来增强模型效果；
• 如果别的方法不能明显提升模型表现，并且感觉模型的共线性影响了模型效果，那统计学VIF的方法可以使用，但sklearn中没有VIF的功能。

4. python后验思想：先得出结果，再管它的实现过程；如果模型效果跑得好，管他怎么实现的呢。

高效嵌入法embedded

L1正则化+嵌入发模块SelectFromModel，高效筛选特征。
（注：尽量保留原数据上的信息，让模型在降维后的数据上拟合效果优秀；我们不考虑测试集与训练集的问题，将所有的数据全放入模型中降维。）

让模型拟合效果更好的调整方法：

1. 调节SelectFromModel类的参数threshold

• 嵌入法的阈值，将所有特征系数低于这个阈值的特征全部筛掉；
• 默认None，SelectFromModel只根据L1的结果选择特征；
• 调整threshold后，SelectFromModel就不只是根据L1正则化来选择特征，而是根据属性coef_中特征的系数来选择；
• 调整threshold的值，画其学习曲线，就可以显式观察出让模型效果最好的threshold值；- - - 但这种方法一般效果不好，画出学习曲线后，会发现如果阈值过大，被删除的特征越多，模型效果也越来越差，模型效果最好的情况下一般需要17个特征以上。

LR_ = LR(solver="liblinear",C=0.9,random_state=420)

fullx = []
fsx = []
threshold = np.linspace(0,abs((LR_.fit(data.data,data.target).coef_)).max(),20)
k=0
for i in threshold:
    X_embedded = SelectFromModel(LR_,threshold=i).fit_transform(data.data,data.target)
    fullx.append(cross_val_score(LR_,data.data,data.target,cv=5).mean())
    fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=5).mean())
    print((threshold[k],X_embedded.shape[1]))
    k+=1
plt.figure(figsize=(20,5))
plt.plot(threshold,fullx,label="full")
plt.plot(threshold,fsx,label="feature selection")
plt.xticks(threshold)
plt.legend()
plt.show()

2. 调节逻辑回归参数C，画C的学习曲线来确定最佳的C值

fullx = []
fsx = []
C=np.arange(0.01,10.01,0.5)
for i in C:
    LR_ = LR(solver="liblinear",C=i,random_state=420)
    fullx.append(cross_val_score(LR_,data.data,data.target,cv=10).mean())
    X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
    fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=10).mean())
    
print(max(fsx),C[fsx.index(max(fsx))])
plt.figure(figsize=(20,5))
plt.plot(C,fullx,label="full")
plt.plot(C,fsx,label="feature selection")
plt.xticks(C)
plt.legend()
plt.show()

再细化C的学习曲线，得出：

最佳的C值是：6.079999999999999
效果达到了：0.9561090225563911

系数累加法

• 原理简单，但是比较麻烦；
• 使用系数coef_，找出曲线由锐利变平滑的转折点，转折点之前被累加的特征都是我们需要的，转折点之后的我们都不需要；
• 需要先对特征系数进行从大到小的排序，且确保我们知道排序后的每个系数对应的原始特征的位置，才能够正确找出那些重要的特征。因此比较麻烦，不如使用嵌入法方便。

包装法

• 直接设定我们需要的特征个数，逻辑回归在现实中运用时，可能会有”需要5~8个变量”这种需求，包装法此时就非常方便了；
• 具体可以参考数据预处理和特征工程那一块内容。

梯度下降

对于二元逻辑回归来说，求θ的方法有很多种：

• 梯度下降法（最著名）
• 坐标下降法
• 牛顿法

参数max_iter

sklearn中梯度下降法求逻辑回归调节最大迭代次数的参数，每一次θ都沿着梯度相反的方向以一定的步长迭代，使损失函数越来越小，直到求出使损失函数最小的θ。

梯度

使函数上升最快的方向，其反方向是使函数下降最快的方向。

逻辑回归中的损失函数：

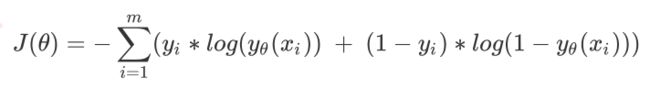
对其自变量θ求偏导，得：

迭代的公式为：

• θj+1：第j次迭代后的参数向量；
• θj：第j次迭代前的参数向量；
• α：步长；

步长

步长不是一个确定的物理距离，也不是梯度下降过程中任何距离的直接变化，而是梯度向量大小d的一个比例。

• 步长过大，很难求出使J(θ)最小的θ；
• 步长过小，迭代的次数特别多，电脑处理得很慢；
  

属性n_iter_

调用查询本次求解所需的实际迭代次数

• max_iter过大，实际迭代次数并不需要这么多，只要找到使损失函数最小的值就立刻停止迭代。因此调用n_iter_得到的值一定会比max_iter小；
• max_iter过小，还没找到使损失函数最小的值就停止了迭代，sklearn中就会发出如下警告：

1. solver=“liblinear”，
   
2. solver=“sag”,
   

接口fit

拟合模型

例子

l2 = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(x,y,test_size=0.3,random_state=420)
for i in np.arange(1,201,10):
    lrl2 = LR(penalty="l2",solver="liblinear",C=0.9,max_iter=i)
    lrl2 = lrl2.fit(Xtrain,Ytrain)
    l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
    l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
graph = [l2,l2test]
color = ["black","gray"]
label = ["L2","L2test"]

plt.figure(figsize=(20,5))
for i in range(len(graph)):
    plt.plot(np.arange(1,201,10),graph[i],color[i],label=label[i])
plt.legend(loc=4)
plt.xticks(np.arange(1,201,10))
plt.show()

d:\python38\lib\site-packages\sklearn\svm\_base.py:985: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  warnings.warn("Liblinear failed to converge, increase "
d:\python38\lib\site-packages\sklearn\svm\_base.py:985: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  warnings.warn("Liblinear failed to converge, increase "
d:\python38\lib\site-packages\sklearn\svm\_base.py:985: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  warnings.warn("Liblinear failed to converge, increase "

#我们可以使用属性.n_iter_来调用本次求解中真正实现的迭代次数
lr=LR(penalty="l2",solver="liblinear",C=0.9,max_iter=300).fit(Xtrain,Ytrain)
lr.n_iter_

array([25], dtype=int32)，即实际25次迭代。

（不管系统报不报红条，只要模型效果好就别管那些）

二元回归与多元回归

sklearn中提供了多种处理多分类问题的方法：
（这两种方法都要配合L1/L2正则项来实现）

• 一对多(OvR)：在sklearn中表示为"ovr"，将多个类别中的一个指定为1，其余类别全指定为0；
• 多对多(MvM)：在sklearn中表示为"multinominal"，将多个类别中的多个指定为1，其余类别全指定为0。

参数solver

控制使用不同的求解器求解参数θ，有五种选择：

（liblinear是二分类专用，默认求解器）

参数multi_class

告诉模型我们预测的模型是什么分类类型的，默认"auto"。

• “ovr”：问题为二分类问题 / 使用"一对多问题"来处理多分类问题；
• “multinomial”：处理多分类问题，但是当solver="liblinear"时不能用；
• “auto”：跟分类问题和其他参数系统自己确定选用上面哪个。
• 注：在0.22版本后"ovr"更改为"auto"。

例子

from sklearn.datasets import load_iris
iris = load_iris()
for multi_class in ('multinomial', 'ovr'):
    clf = LR(solver='sag', max_iter=5000, random_state=42,multi_class=multi_class).fit(iris.data, iris.target)
#打印两种multi_class模式下的训练分数
#%的用法，用%来代替打印的字符串中，想由变量替换的部分。%.3f表示，保留三位小数的浮点数。%s表示，字符串。
#字符串后的%后使用元祖来容纳变量，字符串中有几个%，元祖中就需要有几个变量
print("training score : %.3f (%s)" % (clf.score(iris.data, iris.target),
multi_class))

training score : 0.953 (ovr)

如果max_iter很小，会报红条警告。

样本不均衡

在数据中，可能有一类占很大的比例，还有一类只占很小的比例，导致误分类的代价很高。

eg：在银行要判断“一个新客户是否会违约”，通常不违约的人vs违约的人会是99：1的比例，真正违约的人其实是非常少的。这种分类状况下，即便模型要么也不做，全把所有人都当成不会违约的人，正确率也能有99%，这使得模型评估指标变得毫无意义，根本无法达到我们的“要识别出会违约的人”的建模目的。

参数class_weight

对标签进行一定的均衡：

• None：默认，给所有的类别同样的权重，如果只希望对样本进行均衡，不填即可；
• ‘balanced’：误分类代价很高的时候使用，解决样本不均衡问题。

clf = LR(solver='sag', max_iter=5000, random_state=42,multi_class='multinomial',class_weight=None).fit(iris.data, iris.target)

一些其它样本均衡的方法

• 上采样(最好用)：增加少数类的样本；（在下面的案例中会介绍）
• 下采样：减少多数类的样本。

案例：用逻辑回归制作评分卡

评分卡简介

• 场景：银行借贷；
• 评分卡（定义） 一 以分数形式衡量一个客户的信用风险大小的手段；
  （评分越高，信用越好，风险越小）

1. 评估个人信用程度的方法：
   A、B、C、D卡，（我们这个例子中的评分卡即为A卡，又称"申请信用评级"，用于相关融资类业务中新用户的主体评级）
2. 评估企业的信用评级，按融资主体的融资用途分类的模型有：
   企业融资模型、现金流融资模型、项目融资模型等

模型开发过程

数据分析（模型卡建立及检验）步骤

%matplotlib inline
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression as LR

data=pd.read_csv(r"C:\Users\86138\Desktop\华北电力大学\sklearn完整课件与代码+西瓜书\机器学习Sklearn\05逻辑回归与评分卡\rankingcard.csv",index_col=0)

去掉重复值

• 现实世界中，可能会出现重复值；
• 比较特殊的一类重复值的情况是：确实出现了两个及以上的人各项信息都一样，但是就不是同一个人，这种情况也把它当作重复值来计算；

data.drop_duplicates(inplace=True)

注意：每次去重后其索引值不变，因此需要重新设置索引

data.index=range(data.shape[0])

填补缺失值

数据中有两类：

• 缺的比较多，缺了20000多条，不能全部删除；
• 缺的比较少，只缺了4000多条，可以全部删除；

data.isnull().sum()/data.shape[0] #每个特征的缺失值占该特征总数的比例
#等价于data.isnull().mean()

#可以直接删除那一点缺失值或者说也可以用均值填补它
data["NumberOfDependents"].fillna(int(data["NumberOfDependents"].mean()),inplace=True)

可以使用随机森林填补缺失值：“既然我可以使用A，B，C去预测Z，那我也可以使用A，C，Z去预测B”的思想来填补缺失值”

接口predict

根据已知模型进行预测

def fill_missing_rf(x,y,to_fill):
    """
 使用随机森林填补一个特征的缺失值的函数
 参数：
 X：要填补的特征矩阵
 y：完整的，没有缺失值的标签
 to_fill：字符串，要填补的那一列的名称
 """
#构建新特征矩阵和标签
    df=x.copy()
    fill=df.loc[:,to_fill]
    df=pd.concat([df.loc[:,df.columns!=to_fill],pd.DataFrame(y)],axis=1)
#找出训练集和测试集
    ytrain=fill[fill.notnull()]
    ytest=fill[fill.isnull()]
    xtrain=df.iloc[ytrain.index,:]
    xtest=df.iloc[ytest.index,:]
#用随机森林预测并填补缺失值
    from sklearn.ensemble import RandomForestRegressor as rfr
    rfr=rfr(n_estimators=100)
    rfr=rfr.fit(xtrain,ytrain)
    ypredict=rfr.predict(xtest)
    
    return ypredict

x=data.iloc[:,1:]
y=data['SeriousDlqin2yrs']
to_fill="MonthlyIncome"
y_pred=fill_missing_rf(x,y,to_fill)
data.loc[data.loc[:,"MonthlyIncome"].isnull(),"MonthlyIncome"]=y_pred

注：如果删了一些数据，别忘了重新设置索引。

描述性统计确定异常值

• 异常值不一定都是错误的，有的异常值甚至是我们的重点研究对象，（eg：一个人的工资特别高），要排除的是一些不太符合实际的值（eg：一个人的年龄是负的）。
• 寻找异常值的方法：

1. 箱线法 一 只能用于特征有限的情况，如果有几百个特征又无法成功降维或特征选择不管用，还是用3σ法好；
2. 3σ法

data.describe([0.01,0.1,0.25,0.5,0.9,0.99]).T#'DataFrame' object转置

(data["age"]==0).sum()#只有一个，应该是输入错误
data=data[data["age"]!=0] #把这个异常值删掉
data[data.loc[:,'NumberOfTimes90DaysLate']>90].count()
data[data.loc[:,'NumberOfTimes90DaysLate']<90]
data.index=range(data.shape[0])

量纲不需要统一，数据分布也不需要标准化

所用的数据都是业务员进行判断的依据，如果数据标准化过，那么原始数据对应的信息也会丢失，甚至出现业务员看不懂数据的现象。

样本不均衡问题解决方案

本例使用上采样法

x=data.iloc[:,1:]
y=data.iloc[:,0]
y.value_counts()

n_sample=x.shape[0]

n_1_sample = y.value_counts()[1]
n_0_sample = y.value_counts()[0]

print('样本个数：{}; 1占{:.2%}; 0占{:.2%}'.format(n_sample,n_1_sample/n_sample,n_0_sample/n_sample))

样本个数：149390; 1占6.70%; 0占93.30%

'''
样本不均衡:上采样法解决
'''
import imblearn
#imblearn是专门用来处理不平衡数据集的库，在处理样本不均衡问题中性能高过sklearn很多
#imblearn里面也是一个个的类，也需要进行实例化，fit拟合，和sklearn用法相似
from imblearn.over_sampling import SMOTE
sm = SMOTE(random_state=42) #实例化
x,y = sm.fit_resample(x,y)
n_sample_ = x.shape[0]
pd.Series(y).value_counts()
n_1_sample = pd.Series(y).value_counts()[1]
n_0_sample = pd.Series(y).value_counts()[0]
print('样本个数：{}; 1占{:.2%}; 0占{:.2%}'.format(n_sample_,n_1_sample/n_sample_,n_0_sample/n_sample_))

样本个数：278762; 1占50.00%; 0占50.00%

#将上采样后的数据存储在新的csv文件中
from sklearn.model_selection import train_test_split
x = pd.DataFrame(x)
y = pd.DataFrame(y)
X_train, X_vali, Y_train, Y_vali = train_test_split(x,y,test_size=0.3,random_state=420)
model_data = pd.concat([Y_train, X_train], axis=1)
model_data.index = range(model_data.shape[0])
model_data.columns = data.columns
vali_data = pd.concat([Y_vali, X_vali], axis=1)
vali_data.index = range(vali_data.shape[0])
vali_data.columns = data.columns
model_data.to_csv(r"C:\Users\86138\Desktop\华北电力大学\model_data.csv")
vali_data.to_csv(r"C:\Users\86138\Desktop\华北电力大学\vali_data.csv")

分箱问题

需要知道的一些分箱知识：

• 将连续型变量离散化；
• 箱子的个数不要太多，10个及以下就好；
• 离散化连续型变量必然伴随着信息的损失，箱子越少，信息损失越大；

IV 一 代表：特征的信息及特征对模型的贡献，可以作为衡量指标。

• N：这个特征下箱子的个数；
• i：每个箱子的编号；
• good%：箱内优质客户占整个特征中所有优质客户的比例；
• bad%：箱内坏客户占整个特征中所有坏客户的比例；
• 
  银行业中用来衡量违约概率的指标（即任务权重）。woe越大，优质客户越多；反之越少

< 0.03  特征几乎不带有效信息，对模型没有贡献，这种特征可以被删除
0.03 ~ 0.09  有效信息很少，对模型的贡献度低
0.1 ~ 0.29  有效信息一般，对模型的贡献度中等
0.3 ~ 0.49  有效信息较多，对模型的贡献度较高
>=0.5  有效信息非常多，对模型的贡献超高并且可疑

• 注：IV值并不是越大越好，要找IV的大小和箱子个数的平衡点；
• 对特征进行分箱，在计算每个特征在每个箱子数下的woe值，利用IV的曲线，找出最合适的箱子个数

分箱要达到的效果：“组间差异大，组内差异小”

• eg：对每个评分卡模型来说，即不同箱子的人的违约概率差距大（即woe差距大），且每个箱子内坏客户所占比例（bad%）不同；
• 检验两个箱子的相似性的方法：卡方检验，即若卡方检验的p值较大，说明他们非常相似，可以合并为一个箱子

对一个特征进行分箱的步骤：

1. 连续型变量→ 一组数量较多的分类型变量；eg：将几万个样本分成50组/100组
2. 确保每个组中都要有两种类别（0/1）的变量，否则IV无法计算；
3. 对相邻的组进行卡方检验，将p值很大的组合并，直至剩下的组数不大于设定的N；
4. 让一个特征分别分成[2，3，4，…，20]箱，计算每个分箱情况下的IV值并可视化，找出最佳分箱个数；
5. 分箱完毕后，计算每个箱的woe值和bad%，观察分箱效果；

上述5个步骤完成后，对每个特征都进行分箱，观察他们的IV值，由此选取最合适的特征。

#将选择最佳分享个数的方法包装为函数
import scipy
import matplotlib.pyplot as plt
def graphforbestbin(DF, X, Y, n=5,q=20,graph=True):
#自动最优分箱函数，基于卡方检验的分箱
#参数：
#DF: 需要输入的数据
#X: 需要分箱的列名
#Y: 分箱数据对应的标签 Y 列名
#n: 保留分箱个数
#q: 初始分箱的个数
#graph: 是否要画出IV图像
#区间为前开后闭 (]

#等频分箱
    DF=DF[[X,Y]].copy()
    DF["qcut"],bins = pd.qcut(DF[X], retbins=True, q=q,duplicates="drop")
    coount_y0 = DF.loc[DF[Y]==0].groupby(by="qcut").count()[Y]
    coount_y1 = DF.loc[DF[Y]==1].groupby(by="qcut").count()[Y]
    num_bins = [*zip(bins,bins[1:],coount_y0,coount_y1)]
#确保每个箱子中含有（0和1）两种类别的数据
    for i in range(q):
        if 0 in num_bins[0][2:]:
            num_bins[0:2] = [(
            num_bins[0][0],
            num_bins[1][1],
            num_bins[0][2]+num_bins[1][2],
            num_bins[0][3]+num_bins[1][3])]
            continue

        for i in range(len(num_bins)):
            if 0 in num_bins[i][2:]:
                num_bins[i-1:i+1] = [(
                    num_bins[i-1][0],
                    num_bins[i][1],
                    num_bins[i-1][2]+num_bins[i][2],
                    num_bins[i-1][3]+num_bins[i][3])]
                break
        else:
            break
#计算woe值
    def get_woe(num_bins):
        columns = ["min","max","count_0","count_1"]
        df = pd.DataFrame(num_bins,columns=columns)
        df["total"] = df.count_0 + df.count_1
        df["percentage"] = df.total / df.total.sum()
        df["bad_rate"] = df.count_1 / df.total
        df["good%"] = df.count_0/df.count_0.sum()
        df["bad%"] = df.count_1/df.count_1.sum()
        df["woe"] = np.log(df["good%"] / df["bad%"])
        return df
#计算iv值
    def get_iv(df):
        rate = df["good%"] - df["bad%"]
        iv = np.sum(rate * df.woe)
        return iv
#卡方检验，将箱子合并，直至达到指定的箱子数n
    IV = []
    axisx = []
    while len(num_bins) > n:
        pvs = []
        for i in range(len(num_bins)-1):
            x1 = num_bins[i][2:]
            x2 = num_bins[i+1][2:]
            pv = scipy.stats.chi2_contingency([x1,x2])[1]
            pvs.append(pv)
        i = pvs.index(max(pvs))
        num_bins[i:i+2] = [(
          num_bins[i][0],
          num_bins[i+1][1],
          num_bins[i][2]+num_bins[i+1][2],
          num_bins[i][3]+num_bins[i+1][3])]
        bins_df = pd.DataFrame(get_woe(num_bins))
        axisx.append(len(num_bins))
        IV.append(get_iv(bins_df))
#是否画图
    if graph:
        plt.figure()
        plt.plot(axisx,IV)
        plt.xticks(axisx)
        plt.xlabel("number of box")
        plt.ylabel("IV")
        plt.show()
    return bins_df

对所有特征进行分箱：

model_data.columns
for i in model_data.columns[1:-1]:
	print(i)
	graphforbestbin(model_data,i,"SeriousDlqin2yrs",n=2,q=20)

并不是所有的特征都可以用这个方法来分箱，如果不能，需要自己定义分箱

auto_col_bins = {"RevolvingUtilizationOfUnsecuredLines":6,
        "age":5,
        "DebtRatio":4,
        "MonthlyIncome":3,
        "NumberOfOpenCreditLinesAndLoans":5}
#不能使用自动分箱的变量
hand_bins = {"NumberOfTime30-59DaysPastDueNotWorse":[0,1,2,13]
      ,"NumberOfTimes90DaysLate":[0,1,2,17]
      ,"NumberRealEstateLoansOrLines":[0,1,2,4,54]
      ,"NumberOfTime60-89DaysPastDueNotWorse":[0,1,2,8]
      ,"NumberOfDependents":[0,1,2,3]}
#保证区间覆盖使用 np.inf替换最大值，用-np.inf替换最小值
hand_bins = {k:[-np.inf,*v[:-1],np.inf] for k,v in hand_bins.items()}

bins_of_col = {}
# 生成自动分箱的分箱区间和分箱后的 IV 值
for col in auto_col_bins:
  bins_df = graphforbestbin(model_data,col
              ,"SeriousDlqin2yrs"
              ,n=auto_col_bins[col]
              #使用字典的性质来取出每个特征所对应的箱的数量
              ,q=20
              ,graph=False)
  bins_list = sorted(set(bins_df["min"]).union(bins_df["max"]))
  #保证区间覆盖使用 np.inf 替换最大值 -np.inf 替换最小值
  bins_list[0],bins_list[-1] = -np.inf,np.inf
  bins_of_col[col] = bins_list
  #合并手动分箱数据  
bins_of_col.update(hand_bins)
bins_of_col

计算模型的woe值并映射到原数据上

def get_woe(df,col,y,bins):
  df = df[[col,y]].copy()
  df["cut"] = pd.cut(df[col],bins)
  bins_df = df.groupby("cut")[y].value_counts().unstack()
  woe = bins_df["woe"] =
np.log((bins_df[0]/bins_df[0].sum())/(bins_df[1]/bins_df[1].sum()))
  return woe
#将所有特征的WOE存储到字典当中
woeall = {}
for col in bins_of_col:
  woeall[col] = get_woe(model_data,col,"SeriousDlqin2yrs",bins_of_col[col])
woeal

#不希望覆盖掉原本的数据，创建一个新的DataFrame，索引和原始数据model_data一模一样
model_woe = pd.DataFrame(index=model_data.index)
#将原数据分箱后，按箱的结果把WOE结构用map函数映射到数据中
model_woe["age"] = pd.cut(model_data["age"],bins_of_col["age"]).map(woeall["age"])
#对所有特征操作可以写成：
for col in bins_of_col:
  model_woe[col] = pd.cut(model_data[col],bins_of_col[col]).map(woeall[col])
#将标签补充到数据中
model_woe["SeriousDlqin2yrs"] = model_data["SeriousDlqin2yrs"]
#这就是我们的建模数据了
model_woe.head(

建模与模型验证

#处理测试集
vali_woe = pd.DataFrame(index=vali_data.index)
for col in bins_of_col:
  vali_woe[col] = pd.cut(vali_data[col],bins_of_col[col]).map(woeall[col])
vali_woe["SeriousDlqin2yrs"] = vali_data["SeriousDlqin2yrs"]
vali_X = vali_woe.iloc[:,:-1]
vali_y = vali_woe.iloc[:,-1]

接口score

给定测试数据和标签的平均准确度作为模型的评分标准

X = model_woe.iloc[:,:-1]
y = model_woe.iloc[:,-1]
from sklearn.linear_model import LogisticRegression as LR
lr = LR().fit(X,y)
lr.score(vali_X,vali_y)

返回的结果一般，我们可以试着使用C和max_iter的学习曲线把逻辑回归的效果调上去

c_1 = np.linspace(0.01,1,20)
c_2 = np.linspace(0.01,0.2,20)
score = []
for i in c_2:
  lr = LR(solver='liblinear',C=i).fit(X,y)
  score.append(lr.score(vali_X,vali_y))
plt.figure()
plt.plot(c_2,score)
plt.show()
lr.n_iter_
score = []
for i in [1,2,3,4,5,6]:
  lr = LR(solver='liblinear',C=0.025,max_iter=i).fit(X,y)
  score.append(lr.score(vali_X,vali_y))
plt.figure()
plt.plot([1,2,3,4,5,6],score)
plt.show()

从准确率来看，模型效果一般，下面看ROC曲线上的效果：

接口predict_proba

预测所提供的测试集X中样本点归属于各个标签的概率

import scikitplot as skplt
#%%cmd
#pip install scikit-plot
vali_proba_df = pd.DataFrame(lr.predict_proba(vali_X))
skplt.metrics.plot_roc(vali_y, vali_proba_df,
           plot_micro=False,figsize=(6,6),
           plot_macro=False)

制作评分卡

• 上面使用准确率和ROC曲线验证模型的预测能力；
• 将逻辑回归转化为评分卡分数：
  

1. A：“补偿”
2. B：“刻度”
3. log（odds）：代表一个人违约的可能性

• 逻辑回归的结果为：
  

4. A和B可以根据两个假设的分支带入求出，eg：
   

import numpy as np
#求出A，B值
B = 20/np.log(2)
A = 600 + B*np.log(1/60)
B,A


base_score = A - B*lr.intercept_
base_score

score_age = woeall["age"] * (-B*lr.coef_[0][0])
score_ag

file = "C:/Users/86138/Desktop/华北电力大学/ScoreData.csv"
#open是用来打开文件的python命令，第一个参数是文件的路径+文件名，如果你的文件是放在根目录下，则你只需要文件名就好
#第二个参数是打开文件后的用途，"w"表示用于写入，通常使用的是"r"，表示打开来阅读
#首先写入基准分数
#之后使用循环，每次生成一组score_age类似的分档和分数，不断写入文件之中
with open(file,"w") as fdata:
    fdata.write("base_score,{}\n".format(base_score))
for i,col in enumerate(X.columns):
    score = woeall[col] * (-B*lr.coef_[0][i])
    score.name = "Score"
    score.index.name = col
    score.to_csv(file,header=True,mode="a")

属性intercept_

-逻辑回归预测函数的截距(/偏差)；

• 如果fit_intercept设置为False，则返回0；
• 若问题是二分类问题，则intercept_具有结构（1，）；
• 若multi_class=“multinominal”，intercept_对应于1(True)，- intercept_对应于0(False)；

其它不常用参数

其它不常用属性

无

其它不常用接口