机器学习（三）——梯度下降

在机器学习（二）——线性回归中已经使用梯度下降方法来最小化损失函数，本篇就简要介绍一下梯度下降算法。

1. 引言

1.1 对梯度的理解

借用百度上对梯度的定义：梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。
简单来说：梯度就是一个函数最陡的方向。

更多关于梯度、偏导数、方向导数可参考：链接

1.2 举例

我们举个例子来理解：

假设现有一个二元函数：$J({\theta }_1,{\theta }_2)$，假设 $J_{{\theta }_0}(a,b)$ 和 $J_{{\theta }_1}(a,b)$ 分别为函数在(a, b)处的偏导数，则梯度：
$$\nabla J(a,b)=(J_{{\theta }_0}(a,b),J_{{\theta }_1}(a,b))$$
即梯度是由偏导数构成的向量。

(a,b)处的方向导数为：
$$\begin{array}{rl}& (J_{{\theta }_0}(a,b),J_{{\theta }_1}(a,b))\cdot (\cos \theta ,\sin \theta )\\ & =|(J_{{\theta }_0}(a,b),J_{{\theta }_1}(a,b))|\cdot |1|\cdot \cos \beta \\ & =|\nabla J(a,b)|\cdot \cos \beta \end{array}$$
其中$\beta$为梯度 $\nabla J(a,b)$ 与 $u=(\cos \theta ,\sin \theta )$ 之间的夹角。

则：
（1）$\beta =0$时，$\nabla J(a,b)$ 与 $u$ 同向，此时方向导数取最大值， $max=|\nabla J(a,b)|$
（2）$\beta =\pi$ 时，$\nabla J(a,b)$ 与 $u$ 反向，此时方向导数取最小值， $min=-|\nabla J(a,b)|$

2. 对梯度下降的理解

借用吴恩达老师的话，把下降比作下山，那么梯度下降就是找一个方向，沿着该方向能最快下山。

2.1 算法定义

吴恩达老师的PPT上这样定义梯度下降算法：（针对二元函数$J({\theta }_0,{\theta }_1)$）

即通过不断更新${\theta }_j$的值，直到收敛。每次更新时，都会令${\theta }_j$减去一个值，这个值就是$\alpha$（$\alpha$是学习率，它决定了每次梯度下降时走的步长）乘以对应的偏导数。

2.2 算法理解

为了更直观的理解梯度下降中$\theta$的更新过程，我们用一元函数举例子，设$J(\theta )$是关于$\theta$的一元函数：

根据算法的定义我们知道梯度下降算法要做的是：
$$\theta =\theta -\alpha \frac{dJ(\theta )}{d\theta }$$
由于这里举的例子是一元函数，所以偏导数就直接用导数表示。
（1）对于图（a）
$\theta$初始值处对应的导数是一个正数（切线的斜率为正），$\theta$值更新时，就是减去一个正值，因此$\theta$会向左移动，即向着最低点靠近；
（2）对于图（b）
$\theta$初始值处对应的导数是一个负数（切线的斜率为负），$\theta$值更新时，就是减去一个负值，也就是加上一个正值，因此$\theta$会向右移动，即向着最低点靠近。

由此可知，梯度下降算法会逐步找到函数的（局部）最小值。

3. 模拟梯度下降过程

说明：代码编写和测试均在notebook中实现

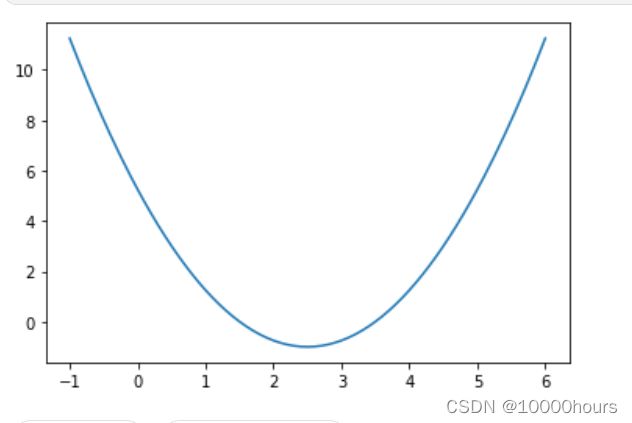
3.1 绘制测试函数

先绘制出测试用的函数y=(x-2.5)^2 - 1：

3.2 模拟梯度下降的过程

epsilon = 1e-8 # 误差
alpha = 0.1 # 学习率

# 函数的定义
def J(theta):
    return (theta - 2.5)**2 - 1.

# 导数的定义
def dJ(theta):
    return 2*(theta - 2.5)

# 梯度下降（这里说梯度下降不太准确，因为这里用的是一元函数的导数）
theta = 0.0
while True:
    gradient = dJ(theta) # 计算导数
    last_theta = theta # 记录上一个自变量
    theta = theta - alpha * gradient # 更新自变量
    
    if (abs(J(theta) - J(last_theta)) < epsilon): # 当两个函数值之差小于误差时就停止下降
        break
        
print(theta)
print(J(theta))

最终得到的theta值和其对应的函数值如下：

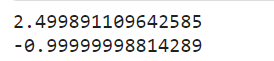
基本接近函数的最小点和最小值。

3.3 下降过程

将这一过程绘制出来，直观的看一下下降的过程：

可以看到，从我们设置的初始值0开始，逐渐沿着函数下降的方向走，而且走的步子越来越小。
这也对应了吴恩达老师讲的：“当我们接近局部最低点时，梯度下降法会自动采取更小的幅度”。当接近局部最低点时，导数值接近0，也就是说，接近局部最低点时导数值也相应的会变小，“所以梯度下降将自动采取较小的幅度，这就是梯度下降的做法。所以实际上没有必要再另外减小。”

3.4 不同 $\alpha$ 对下降的影响

上文说到 $\alpha$ 的大小决定了每次下降的步长，也就是每次下山要迈多大的步子，那就采用不同的 $\alpha$ 值测试一下，看看不同 $\alpha$ 值对应的下降过程是怎样的。
（1）$\alpha$ = 0.01

我们之前看到了$\alpha =0.1$时的情况，当$\alpha$变为0.01时可以明显的看到每次的步长变得更小，而且走的步数也多了。
（2）$\alpha =0.8$

当$\alpha$变为0.8时，下降情况就和之前有所不同了，有些像摇摆的方式往下走，但是最后也收敛了。
（3）$\alpha =1.1$

从图中可以看到当$\alpha$取值过大时，最后会导致不收敛，不往最低点走了，反而往外跑了。

从测试结果来看，学习率$\alpha$的选择对梯度下降是很重要的，若$\alpha$太小，会导致收敛速度太慢；若$\alpha$太大，会导致结果不收敛甚至发散。

3.5 初始值的选取

我们在3.4看到了不同的学习率值对下降过程的影响，那初始值对下降过程是否有影响呢？答案是肯定的。

3.5.1 一元函数

在之前的测试中，我们选择的初始值都是0， 0在函数$y=(x-2.5{)}^2-1$最低点的附近，但是如果一开始就将初始值选在函数的最低点会怎样？
选取初始值为2.5，下降过程为：

可以看到小红点就没动，一直待在最低点。因为我们一开始就将初始值放在了（局部）最低点，此处的导数值为0，那么在这一步更新时，$\theta$的值不会变：

 theta = theta - alpha * gradient # 更新自变量

也就是说此时梯度下降根本没有更新$\theta$的值，也就是开始即结束，此处再引用吴恩达老师的话：“这也解释了为什么即使学习速率保持不变时，梯度下降也可以收敛到局部最低点”

同样的，假设我们选取的初始值是5，在学习率合适的情况下，$x$的更新是向左的，下降过程也是向左走的。

3.5.2 二元函数

那我们再思考一个问题，倘若函数是二元函数 $J({\theta }_0,{\theta }_1)$ ，假设函数如下图所示。
注：图片来自吴恩达老师的PPT。

我们可以看到函数有两个较低的点（图中红色箭头所指），那么选择不同的初始值，最后就会下降到不同的位置：

同样地，假设我们一开始就在一个较低点，该位置的梯度为0，那么梯度下降就不会更新$\theta$的值，也就是说我们会一直待在这个较低点。

通过上文的描述我们也就能知道了，梯度下降找到的可能不是函数的最小值，而是函数的局部最小值。

4. 梯度下降实践

简单了解了梯度下降算法之后，我们尝试在线性回归中使用梯度下降算法来寻找损失函数的最小值。

4.1 梯度下降的代码实现

# theta为参数，X_b为增添了X0列之后的自变量
def J(theta, X_b, y):
    try:
        return np.sum((y - X_b.dot(theta)) ** 2) / (2 * len(X_b)) # 损失函数J
    except:
        return float('inf')
    
def dJ(theta, X_b, y):
    res = np.empty(len(theta))
    res[0] = np.sum(X_b.dot(theta) - y) # X0恒为1
    for i in range(1, len(theta)):
        res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])
    return res / len(X_b)

def gradient_descent(X_b, y, initial_theta, eta, n_iter=1e4, epsilon=1e-8):
    theta = initial_theta
    cur_iter = 0
    
    while cur_iter < n_iter:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta * gradient
        if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
            break
        
        cur_iter += 1
        
    return theta

4.2 测试

4.2.1 单特征样本数据

我们使用只有一个特征的样本数据进行测试，随机生成样本数据：

import numpy as np
import matplotlib.pyplot as plt

# 使用随机数测试
np.random.seed(999)
x = 2 * np.random.random(size=100)
y = x * 5. + 9. + np.random.normal(size=100)

样本数据在二维平面上展示如下：（其中横轴就对应了样本特征，纵轴对应样本的输出标记）

创建样本数据$X_b$和参数$\theta$:

X = x.reshape(-1, 1) # X.shape : (100, 1)
X_b = np.hstack([np.ones((len(x), 1)), x.reshape(-1, 1)]) # 添加X0
print(X_b.shape)
initial_theta = np.zeros(X_b.shape[1])
print(initial_theta.shape)
eta = 0.01

theta = gradient_descent(X_b, y, initial_theta, eta)
print(theta)

${\theta }_0$ 大约为8.90, ${\theta }_1$ 大约为5.12，计算的结果和我们最初设置的随机数的y = x * 5. + 9. + np.random.normal(size=100)差不多

4.2.2 多特征样本数据

为了方便可视化，我们使用有连个特征的样本数据进行测试：

np.random.seed(999)
x_1 = 2 * np.random.random(size=100)
x_2 = 8 * np.random.random(size=100)
y = 9. + 5. * x_1 + 8. * x_2 + np.random.normal(size=100)


ax = plt.axes(projection='3d')
ax.scatter3D(x_1, x_2, y)
plt.show()

样本数据可视化：

创建样本数据$X_b$和参数$\theta$:

X_b = np.hstack([np.ones((len(x), 1)), x_1.reshape(-1, 1), x_2.reshape(-1, 1)])
print(X_b.shape)
initial_theta = np.zeros(X_b.shape[1])
print(initial_theta.shape)
eta = 0.01

theta = gradient_descent(X_b, y, initial_theta, eta)
print(theta)

${\theta }_0$ 大约为9.00， ${\theta }_1$大约为4.90， ${\theta }_2$约为8.00，对比我们之前设置的函数中的参数大致一样。

5.总结

至此，梯度下降算法的相关内容就整理的差不多了。
（1）首先我们理解了什么是梯度，并了解了梯度、偏导数、方向导数之间的联系；
（2）然后我们直观的理解了梯度下降算法，了解了算法要做的事：通过不断更新$\theta$直到收敛，收敛也就意味着基本到达函数的局部最小值了；
（3）之后我们通过编写代码模拟了梯度下降的过程，了解了学习率$\alpha$以及初始值的选取对下降过程的影响，而且通过二元函数的例子知道了为什么梯度下降收敛到的不一定是函数全局最小值而是局部最小值；
（4）我们又尝试了在线性回归中使用梯度下降来最小化损失函数，以得到最好的拟合效果，并用了不同的样本数据进行测试。

几点说明：
（1）因为本人也是初学者，文章内容可能会有错误和不足，非常欢迎大家指正和补充！
（2）我们通常会看到使用梯度下降寻找损失函数的最小值，但梯度下降算法可以用来寻找任一函数的最小值。
（3）这里再多说一句，吴恩达老师的机器学习真的是经典，B站上也有各大up主上传的视频课，视频地址：地址。虽然视频是很多年前录的，但是理论知识是通用的，我觉得吴恩达老师的理论知识讲的很好。现在很多项目都是用python来做了，github上也有很多开源的项目，大家可以来练练手。
还有一个大佬整理的学习笔记：地址

机器学习（四）——PCA