机器学习和特征工程理论与python代码实现 晓物智联

文章来源于:http://www.52phm.cn/blog/detail/23
最初来源于本人的kesci专栏
- 课题:特征工程理论及代码实现
- 日期:2019.9.21
- 作者:小知同学
描述:本篇比较详细的介绍了特征工程的理论以及代码实现,涵盖数据预处理、特征选择、特征构造、特征降维、
类别不平衡处理等内容,不仅介绍了相关理论以及公式,而且还根据理论公式编写代码实现功能。
本篇特征工程的内容有些地方还不完善,如果大家觉得哪些地方想要补充、想要完善的请在评论区留言完善,
小知同学也会更新上来,进一步完善这篇特征工程专辑,以便大家更好的学习和掌握知识。
算法知识点一般的必备通用认知流程有以下几点:
- 概念及工作原理
- 理论公式及推导
- 优缺点
- 应用场景及意义
- 功能(代码)实现
为什么总结为这几点呢?
第一点是认知知识的初始印象,它能告诉我们这个知识是做什么的,以及它运作的原理。
第二点是作为一个算法从事者的基本功和基本素养,也是核心部分。这部分要掌握算法的具体数学公式以及其运作原理。
第三点是知道各个算法优缺点之后,可以方便根据具体情况选择合理且高效的方法
第四点是明确应用目标方便选择策略和方法
第五点是在学习理论之后的实践部分,这部分是专门提高工程能力的。
往期文章学习
https://www.kesci.com/home/column/5cb43d67e0ad99002cad14d6
1.特征使用方案
-
要实现我们的目标需要哪些数据?
基于业务理解,尽可能找出对应变量有影响的所有变量 -
可用性评估
(1)获取难度
(2)覆盖率
(3)准确率
2.特征获取方案
- 如何获取这些特征?
- 如何存储?
3.数据预处理
数据可划分为结构化数据与非结构化数据,定义如下:
- 结构化数据
代表性的有数值型、字符串型数据 - 非结构化数据
代表的有文本型、图像型、视频型以及语音型数据
3.1.结构化数据预处理
预处理一般可分为缺失值处理、离群值(异常值)处理以及数据变换
3.1.1.缺失值处理
一般来说,未经处理的原始数据中通常会存在缺失值、离群值等,因此在建模训练之前需要处理好缺失值。
缺失值处理方法一般可分为:删除、统计值填充、统一值填充、前后向值填充、插值法填充、建模预测填充和具体分析7种方法。
3.1.1.1.直接删除
理论部分
缺失值最简单的处理方法是删除,所谓删除就是删除属性或者删除样本,删除一般可分为两种情况:
-
删除属性(特征)
如果某一个特征中存在大量的缺失值(缺失量大于总数据量的40%~50%及以上),
那么我们可以认为这个特征提供的信息量非常有限,这个时候可以选择删除掉这一维特征。 -
删除样本
如果整个数据集中缺失值较少或者缺失值数量对于整个数据集来说可以忽略不计的情况下,
那么可以直接删除含有缺失值的样本记录。
注意事项:
如果数据集本身数据量就很少的情况下,不建议直接删除缺失值。
代码实现
构造假数据做演示,就上面两种情况进行代码实现删除。
import numpy as np
import pandas as pd
# 构造数据
def dataset():
col1 = [1, 2, 3, 4, 5, 6, 7, 8, 9,10]
col2 = [3, 1, 7, np.nan, 4, 0, 5, 7, 12, np.nan]
col3 = [3, np.nan, np.nan, np.nan, 9, np.nan, 10, np.nan, 4, np.nan]
y = [10, 15, 8, 12, 17, 9, 7, 14, 16, 20]
data = {'feature1':col1, 'feature2':col2, 'feature3':col3, 'label':y}
df = pd.DataFrame(data)
return df
data = dataset()
data
/opt/conda/lib/python3.6/importlib/_bootstrap.py:219: RuntimeWarning: numpy.dtype size changed, may indicate binary incompatibility. Expected 96, got 88
return f(*args, **kwds)
/opt/conda/lib/python3.6/importlib/_bootstrap.py:219: RuntimeWarning: numpy.dtype size changed, may indicate binary incompatibility. Expected 96, got 88
return f(*args, **kwds)
| feature1 | feature2 | feature3 | label | |
|---|---|---|---|---|
| 0 | 1 | 3.0 | 3.0 | 10 |
| 1 | 2 | 1.0 | NaN | 15 |
| 2 | 3 | 7.0 | NaN | 8 |
| 3 | 4 | NaN | NaN | 12 |
| 4 | 5 | 4.0 | 9.0 | 17 |
| 5 | 6 | 0.0 | NaN | 9 |
| 6 | 7 | 5.0 | 10.0 | 7 |
| 7 | 8 | 7.0 | NaN | 14 |
| 8 | 9 | 12.0 | 4.0 | 16 |
| 9 | 10 | NaN | NaN | 20 |
# 删除属性
def delete_feature(df):
N = df.shape[0] # 样本数
no_nan_count = df.count().to_frame().T # 每一维特征非缺失值的数量
del_feature, save_feature = [], []
for col in no_nan_count.columns.tolist():
loss_rate = (N - no_nan_count[col].values[0])/N # 缺失率
# print(loss_rate)
if loss_rate > 0.5: # 缺失率大于 50% 时,将这一维特征删除
del_feature.append(col)
else:
save_feature.append(col)
return del_feature, df[save_feature]
del_feature, df11 = delete_feature(data)
print(del_feature)
df11
['feature3']
| feature1 | feature2 | label | |
|---|---|---|---|
| 0 | 1 | 3.0 | 10 |
| 1 | 2 | 1.0 | 15 |
| 2 | 3 | 7.0 | 8 |
| 3 | 4 | NaN | 12 |
| 4 | 5 | 4.0 | 17 |
| 5 | 6 | 0.0 | 9 |
| 6 | 7 | 5.0 | 7 |
| 7 | 8 | 7.0 | 14 |
| 8 | 9 | 12.0 | 16 |
| 9 | 10 | NaN | 20 |
# 删除样本
# 从上面可以看出,feature2 的缺失值较少,
# 可以采取直接删除措施
def delete_sample(df):
df_ = df.dropna()
return df_
delete_sample(df11)
| feature1 | feature2 | label | |
|---|---|---|---|
| 0 | 1 | 3.0 | 10 |
| 1 | 2 | 1.0 | 15 |
| 2 | 3 | 7.0 | 8 |
| 4 | 5 | 4.0 | 17 |
| 5 | 6 | 0.0 | 9 |
| 6 | 7 | 5.0 | 7 |
| 7 | 8 | 7.0 | 14 |
| 8 | 9 | 12.0 | 16 |
3.1.1.2.统计值填充
理论部分
-
对于特征的缺失值,可以根据缺失值所对应的那一维特征的统计值来进行填充。
-
统计值一般泛指平均值、中位数、众数、最大值、最小值等,具体使用哪一种统计值要根据具体问题具体分析。
-
注意事项:当特征之间存在很强的类别信息时,需要进行类内统计,效果比直接处理会更好。
比如在填充身高时,需要先对男女进行分组聚合之后再进行统计值填充处理(男士的一般平均身高1.70,女士一般1.60)。
代码实现
使用上面数据帧 df11 作为演示数据集,分别实现使用各个统计值填充缺失值。
# 使用上面 df11 的数据帧作为演示数据
df11
| feature1 | feature2 | label | |
|---|---|---|---|
| 0 | 1 | 3.0 | 10 |
| 1 | 2 | 1.0 | 15 |
| 2 | 3 | 7.0 | 8 |
| 3 | 4 | NaN | 12 |
| 4 | 5 | 4.0 | 17 |
| 5 | 6 | 0.0 | 9 |
| 6 | 7 | 5.0 | 7 |
| 7 | 8 | 7.0 | 14 |
| 8 | 9 | 12.0 | 16 |
| 9 | 10 | NaN | 20 |
# 均值填充
print(df11.mean())
df11.fillna(df11.mean())
feature1 5.500
feature2 4.875
label 12.800
dtype: float64
| feature1 | feature2 | label | |
|---|---|---|---|
| 0 | 1 | 3.000 | 10 |
| 1 | 2 | 1.000 | 15 |
| 2 | 3 | 7.000 | 8 |
| 3 | 4 | 4.875 | 12 |
| 4 | 5 | 4.000 | 17 |
| 5 | 6 | 0.000 | 9 |
| 6 | 7 | 5.000 | 7 |
| 7 | 8 | 7.000 | 14 |
| 8 | 9 | 12.000 | 16 |
| 9 | 10 | 4.875 | 20 |
# 中位数填充
print(df11.median())
df11.fillna(df11.median())
feature1 5.5
feature2 4.5
label 13.0
dtype: float64
| feature1 | feature2 | label | |
|---|---|---|---|
| 0 | 1 | 3.0 | 10 |
| 1 | 2 | 1.0 | 15 |
| 2 | 3 | 7.0 | 8 |
| 3 | 4 | 4.5 | 12 |
| 4 | 5 | 4.0 | 17 |
| 5 | 6 | 0.0 | 9 |
| 6 | 7 | 5.0 | 7 |
| 7 | 8 | 7.0 | 14 |
| 8 | 9 | 12.0 | 16 |
| 9 | 10 | 4.5 | 20 |
# 众数填充
# print(df11.mode())
# 由于众数可能会存在多个,因此返回的是序列而不是一个值
# 所以在填充众数的时候,我们可以 df11['feature'].mode()[0],可以取第一个众数作为填充值
def mode_fill(df):
for col in df.columns.tolist():
if df[col].isnull().sum() > 0: # 有缺失值就进行众数填充
df_ = df.fillna(df11[col].mode()[0])
return df_
mode_fill(df11)
| feature1 | feature2 | label | |
|---|---|---|---|
| 0 | 1 | 3.0 | 10 |
| 1 | 2 | 1.0 | 15 |
| 2 | 3 | 7.0 | 8 |
| 3 | 4 | 7.0 | 12 |
| 4 | 5 | 4.0 | 17 |
| 5 | 6 | 0.0 | 9 |
| 6 | 7 | 5.0 | 7 |
| 7 | 8 | 7.0 | 14 |
| 8 | 9 | 12.0 | 16 |
| 9 | 10 | 7.0 | 20 |
# 最大值/最小值填充
df11.fillna(df11.max())
df11.fillna(df11.min())
| feature1 | feature2 | label | |
|---|---|---|---|
| 0 | 1 | 3.0 | 10 |
| 1 | 2 | 1.0 | 15 |
| 2 | 3 | 7.0 | 8 |
| 3 | 4 | 0.0 | 12 |
| 4 | 5 | 4.0 | 17 |
| 5 | 6 | 0.0 | 9 |
| 6 | 7 | 5.0 | 7 |
| 7 | 8 | 7.0 | 14 |
| 8 | 9 | 12.0 | 16 |
| 9 | 10 | 0.0 | 20 |
3.1.1.3.统一值填充
理论部分
- 对于缺失值,把所有缺失值都使用统一值作为填充词,所谓统一值是指自定义指定的某一个常数。
- 常用的统一值有:空值、0、正无穷、负无穷或者自定义的其他值
注意事项:当特征之间存在很强的类别信息时,需要进行类内统计,效果比直接处理会更好。
比如在填充身高时,需要先对男女进行分组聚合之后再进行统一值填充处理
(男士的身高缺失值使用统一填充值就自定为常数1.70,女士自定义常数1.60)。
代码实现
任然使用数据帧 df11 进行演示,实现统一值填充缺失值的应用。
df11
| feature1 | feature2 | label | |
|---|---|---|---|
| 0 | 1 | 3.0 | 10 |
| 1 | 2 | 1.0 | 15 |
| 2 | 3 | 7.0 | 8 |
| 3 | 4 | NaN | 12 |
| 4 | 5 | 4.0 | 17 |
| 5 | 6 | 0.0 | 9 |
| 6 | 7 | 5.0 | 7 |
| 7 | 8 | 7.0 | 14 |
| 8 | 9 | 12.0 | 16 |
| 9 | 10 | NaN | 20 |
# 统一值填充
# 自定义统一值常数为 10
df11.fillna(value=10)
| feature1 | feature2 | label | |
|---|---|---|---|
| 0 | 1 | 3.0 | 10 |
| 1 | 2 | 1.0 | 15 |
| 2 | 3 | 7.0 | 8 |
| 3 | 4 | 10.0 | 12 |
| 4 | 5 | 4.0 | 17 |
| 5 | 6 | 0.0 | 9 |
| 6 | 7 | 5.0 | 7 |
| 7 | 8 | 7.0 | 14 |
| 8 | 9 | 12.0 | 16 |
| 9 | 10 | 10.0 | 20 |
3.1.1.4.前后向值填充
理论部分
前后向值填充是指使用缺失值的前一个或者后一个的值作为填充值进行填充。
代码实现
任然使用数据帧 df11 作为演示的数据集,实现前后向值填充。
df11
| feature1 | feature2 | label | |
|---|---|---|---|
| 0 | 1 | 3.0 | 10 |
| 1 | 2 | 1.0 | 15 |
| 2 | 3 | 7.0 | 8 |
| 3 | 4 | NaN | 12 |
| 4 | 5 | 4.0 | 17 |
| 5 | 6 | 0.0 | 9 |
| 6 | 7 | 5.0 | 7 |
| 7 | 8 | 7.0 | 14 |
| 8 | 9 | 12.0 | 16 |
| 9 | 10 | NaN | 20 |
df11.fillna(method='ffill') # 前向填充
| feature1 | feature2 | label | |
|---|---|---|---|
| 0 | 1 | 3.0 | 10 |
| 1 | 2 | 1.0 | 15 |
| 2 | 3 | 7.0 | 8 |
| 3 | 4 | 7.0 | 12 |
| 4 | 5 | 4.0 | 17 |
| 5 | 6 | 0.0 | 9 |
| 6 | 7 | 5.0 | 7 |
| 7 | 8 | 7.0 | 14 |
| 8 | 9 | 12.0 | 16 |
| 9 | 10 | 12.0 | 20 |
df11.fillna(method='bfill') # 后向填充
| feature1 | feature2 | label | |
|---|---|---|---|
| 0 | 1 | 3.0 | 10 |
| 1 | 2 | 1.0 | 15 |
| 2 | 3 | 7.0 | 8 |
| 3 | 4 | 4.0 | 12 |
| 4 | 5 | 4.0 | 17 |
| 5 | 6 | 0.0 | 9 |
| 6 | 7 | 5.0 | 7 |
| 7 | 8 | 7.0 | 14 |
| 8 | 9 | 12.0 | 16 |
| 9 | 10 | NaN | 20 |
从上面的后向填充我们发现明显的 Bug:
如果最后一个是缺失值,那么后向填充无法处理最后一个的缺失值;
如果第一个是缺失值,那么前向填充无法处理第一个的缺失值。
因此在进行前后向值填充时,要根据具体情况来进行填充,
一般同时进行前向填充+后向填充就可以解决上面的问题。
3.1.1.5.插值法填充
2019.8.14
工作原理
所谓的插值法,就是在X范围区间中挑选一个或者自定义一个数值,
然后代进去插值模型公式当中,求出数值作为缺失值的数据。
** 1. 多项式插值**
理论公式及推导
已知n+1个互异的点 P 1 : ( x 1 , y 1 ) , P 2 : ( x 2 , y 2 ) , . . . , P n + 1 : ( x n + 1 , y n + 1 ) P1:(x1,y1),P2:(x2,y2),...,P_{n+1}:(x_{n+1},y_{n+1}) P1:(x1,y1),P2:(x2,y2),...,Pn+1:(xn+1,yn+1),
可以求得经过这n+1个点,最高次不超过n的多项式 Y = a 0 + a 1 X + a 2 X 2 + . . . + a n X n Y=a_0+a_1X+a_2X^2+...+a_nX^n Y=a0+a1X+a2X2+...+anXn,
其中计算系数A的公式如下:
A = [ a 0 , a 1 , . . . , a n ] T = X − 1 Y , 其 中 X − 1 是 X 的 逆 矩 阵 A=[a_0,a_1,...,a_n]^T=X^{-1}Y,其中X^{-1}是X的逆矩阵 A=[a0,a1,...,an]T=X−1Y,其中X−1是X的逆矩阵
(1)其中X,Y形式如下,求待定系数A:
X = [ 1 x 1 x 1 2 . . . x 1 n 1 x 2 x 2 2 . . . x 2 n . . . . . 1 x n + 1 x n + 1 2 . . . x n + 1 n ] , Y = [ y 1 y 2 . y n + 1 ] X=\begin{bmatrix} 1&x_1&x_1^2&...&x_1^n\\ 1&x_2&x_2^2&...&x_2^n\\ .&.&.&.&.\\ 1&x_{n+1}&x_{n+1}^2&...&x_{n+1}^n \end{bmatrix},Y=\begin{bmatrix} y_1&\\ y_2&\\ .&\\ y_{n+1}& \end{bmatrix} X=⎣⎢⎢⎡11.1x1x2.xn+1x12x22.xn+12..........x1nx2n.xn+1n⎦⎥⎥⎤,Y=⎣⎢⎢⎡y1y2.yn+1⎦⎥⎥⎤
(2)进行插值的公式, Y = A X Y=AX Y=AX
工作原理
(1)在事先已知的n+1个P点,可以通过A=X^(-1) Y求解得到待定系数A。
(2)假设有一空值,已知X(test_x)值,但Y值(缺失值的填充词)不知道,
由步骤1求解到的待定系数根据公式Y=AX可以求解出缺失值的数值。
import numpy as np
def Polynomial(x, y, test_x):
'''
test_x 的值一般是在缺失值的前几个或者后几个值当中,挑出一个作为参考值,
将其值代入到插值模型之中,学习出一个值作为缺失值的填充值
'''
# 求待定系数
array_x = np.array(x) # 向量化
array_y = np.array(y)
n, X = len(x), []
for i in range(n): # 形成 X 矩阵
l = array_x ** i
X.append(l)
X = np.array(X).T
A = np.dot(np.linalg.inv(X), array_y) # 根据公式求待定系数 A
# 缺失值插值
xx = []
for j in range(n):
k = test_x ** j
xx.append(k)
xx=np.array(xx)
return np.dot(xx, A)
x, y, test_x = [1, 2, 3, 4], [1, 5, 2, 6], 3.5
Polynomial(x, y, test_x)
2.250000000000057
2. lagrange插值
工作原理
可以证明,经过n+1个互异的点的次数不超过n的多项式是唯一存在的。
也就是说,无论是否是使用何种基底,只要基底能张成所需要的空间,都不会影响最终结果。 。
理论公式及推导
已知n+1个互异的点 P 1 : ( x 1 , y 1 ) , P 2 : ( x 2 , y 2 ) , . . . , P n + 1 : ( x n + 1 , y n + 1 ) P1:(x1,y1),P2:(x2,y2),...,P_{n+1}:(x_{n+1},y_{n+1}) P1:(x1,y1),P2:(x2,y2),...,Pn+1:(xn+1,yn+1),令
l i ( x ) = ∏ ( j ≠ i ) ( j = 1 ) n + 1 x − x j x i − x j , 公 式 ( 1 ) l_i(x)=\prod_{(j\ne i)(j=1)}^{n+1}\frac{x-x_j}{x_i-x_j},公式(1) li(x)=(j=i)(j=1)∏n+1xi−xjx−xj,公式(1)
作为插值基底,则Lagrange值 L i ( x ) = ∑ i = 1 n + 1 l i ( x ) y i , 公 式 ( 2 ) L_i(x)=\sum \limits_{i=1}^{n+1}l_i(x)y_i,公式(2) Li(x)=i=1∑n+1li(x)yi,公式(2)
工作原理
(1)先求出插值基底值
(2)再求Lagrange拉格朗日值
def Lagrange(x, y, test_x):
'''
所谓的插值法,就是在X范围区间中挑选一个或者自定义一个数值,
然后代进去插值公式当中,求出数值作为缺失值的数据。
'''
n = len(x)
L = 0
for i in range(n):
# 计算公式 1
li = 1
for j in range(n):
if j != i:
li *= (test_x-x[j])/(x[i]-x[j])
# 计算公式 2
L += li * y[i]
return L
Lagrange(x, y, test_x)
2.25
3.1.1.6.预测填充
理论部分
预测填充思路如下:
(1)把需要填充缺失值的某一列特征(Feature_A)作为新的标签(Label_A)
(2)然后找出与 Label_A 相关性较强的特征作为它的模型特征
(3)把 Label_A 非缺失值部分作为训练集数据,而缺失值部分则作为测试集数据
(4)若 Label_A 的值属于连续型数值,则进行回归拟合;若是类别(离散)型数值,则进行分类学习
(5)将训练学习到评分和泛化能力较好的模型去预测测试集,从而填充好缺失值
代码实现部分
使用 seaborn 模块中内置 IRIS 数据集进行演示,实现使用算法模型进行预测填充。
import seaborn as sns
import numpy as np
import warnings
import matplotlib.pyplot as plt
%matplotlib inline
warnings.filterwarnings('ignore')
dataset = sns.load_dataset('iris')
print(dataset.shape)
print(dataset.isnull().sum())
dataset.head()
(150, 5)
sepal_length 0
sepal_width 0
petal_length 0
petal_width 0
species 0
dtype: int64
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
# (1)把需要填充缺失值的某一列特征(petal_width)作为新的标签(Label_petal_width)
# 将特征 petal_width 处理成含有 30 个缺失值的特征
dataset['Label_petal_length'] = dataset['petal_length']
for i in range(0, 150, 5):
dataset.loc[i, 'Label_petal_length'] = np.nan
print(dataset.isnull().sum())
dataset.head()
sepal_length 0
sepal_width 0
petal_length 0
petal_width 0
species 0
Label_petal_length 30
dtype: int64
| sepal_length | sepal_width | petal_length | petal_width | species | Label_petal_length | |
|---|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa | NaN |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa | 1.4 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa | 1.3 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa | 1.5 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa | 1.4 |
# (2)然后找出与 Label_A 相关性较强的特征作为它的模型特征
# 可以发现特征 sepal_length、petal_width 与 Label_petal_width 有着强关联,
# 因此 sepal_length、petal_width 作为 Label_petal_length 的模型特征
dataset.corr()
| sepal_length | sepal_width | petal_length | petal_width | Label_petal_length | |
|---|---|---|---|---|---|
| sepal_length | 1.000000 | -0.117570 | 0.871754 | 0.817941 | 0.875744 |
| sepal_width | -0.117570 | 1.000000 | -0.428440 | -0.366126 | -0.449716 |
| petal_length | 0.871754 | -0.428440 | 1.000000 | 0.962865 | 1.000000 |
| petal_width | 0.817941 | -0.366126 | 0.962865 | 1.000000 | 0.963768 |
| Label_petal_length | 0.875744 | -0.449716 | 1.000000 | 0.963768 | 1.000000 |
# (3)把 Label_petal_length 非缺失值部分作为训练集数据,而缺失值部分则作为测试集数据
data = dataset[['sepal_length', 'petal_width', 'Label_petal_length']].copy()
train = data[data['Label_petal_length'].notnull()]
test = data[data['Label_petal_length'].isnull()]
print(train.shape)
print(test.shape)
(120, 3)
(30, 3)
# (4)由于 Label_petal_length 的值属于连续型数值,则进行回归拟合
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 将训练集进行切分,方便验证模型训练的泛化能力
x_train, x_valid, y_train, y_valid = train_test_split(train.iloc[:, :2],
train.iloc[:, 2],
test_size=0.3
)
print(x_train.shape, x_valid.shape)
print(y_train.shape, y_valid.shape)
# 使用简单的线性回归进行训练
lr = LinearRegression()
lr.fit(x_train, y_train)
y_train_pred = lr.predict(x_train)
print('>>>在训练集中的表现:', r2_score(y_train_pred, y_train))
y_valid_pred = lr.predict(x_valid)
print('>>>在验证集中的表现:', r2_score(y_valid_pred, y_valid))
(84, 2) (36, 2)
(84,) (36,)
>>>在训练集中的表现: 0.9544599225887372
>>>在验证集中的表现: 0.9304625292045441
# (5)将训练学习到评分和泛化能力较好的模型去预测测试集,从而填充好缺失值
# 由上面来看,模型在训练集以及验证集上的表现相差不大并且效果挺不错的,
# 这说明模型的泛化能力不错,可以用于投放使用来预测测试集
y_test_pred = lr.predict(test.iloc[:, :2])
test.loc[:, 'Label_petal_length'] = y_test_pred
df_no_nan = pd.concat([train, test], axis=0)
print(df_no_nan.isnull().sum())
df_no_nan.head()
sepal_length 0
petal_width 0
Label_petal_length 0
dtype: int64
| sepal_length | petal_width | Label_petal_length | |
|---|---|---|---|
| 1 | 4.9 | 0.2 | 1.4 |
| 2 | 4.7 | 0.2 | 1.3 |
| 3 | 4.6 | 0.2 | 1.5 |
| 4 | 5.0 | 0.2 | 1.4 |
| 6 | 4.6 | 0.3 | 1.4 |
上面就是预测填充的代码示例以及详细讲解。
3.1.1.7.具体分析
[-]参考资料
上面两次提到具体问题具体分析,为什么要具体问题具体分析呢?因为属性缺失有时并不意味着数据缺失,
缺失本身是包含信息的,所以需要根据不同应用场景下缺失值可能包含的信息进行合理填充。
下面通过一些例子来说明如何具体问题具体分析,仁者见仁智者见智,仅供参考:
- “年收入”:商品推荐场景下填充平均值,借贷额度场景下填充最小值;
- “行为时间点”:填充众数;
- “价格”:商品推荐场景下填充最小值,商品匹配场景下填充平均值;
- “人体寿命”:保险费用估计场景下填充最大值,人口估计场景下填充平均值;
- “驾龄”:没有填写这一项的用户可能是没有车,为它填充为0较为合理;
- ”本科毕业时间”:没有填写这一项的用户可能是没有上大学,为它填充正无穷比较合理;
- “婚姻状态”:没有填写这一项的用户可能对自己的隐私比较敏感,应单独设为一个分类,如已婚1、未婚0、未填-1。
3.1.2 离群值处理
3.1.2.1.标准差法
又称为拉依达准则(标准差法),适用于有较多组数据的时候。
工作原理:它是先假设一组检测数据只含有随机误差,对其进行计算处理得到标准偏差,
按一定概率确定一个区间,认为凡超过这个区间的误差,就不属于随机误差而是粗大误差,
含有该误差的数据应予以剔除。
标准差本身可以体现因子的离散程度,是基于因子的平均值μ而定的。在离群值处理过程中,
可通过用μ±nσ来衡量因子与平均值的距离
公式:假设有近似服从正态分布离散数据X=[x1,x2,…,xn],其均值μ与标准差σ分别为:
μ = ∑ i = 1 n x i n , σ = ∑ i = 1 n ( x i − μ ) 2 n \mu=\frac{\sum_{i=1}^nx_i}{n},\sigma=\sqrt \frac{\sum_{i=1}^n(x_i-\mu)^2}{n} μ=n∑i=1nxi,σ=n∑i=1n(xi−μ)2
如何衡量数值是否为离群值?
将区间 [ μ − 3 σ , μ + 3 σ ] [\mu-3\sigma,\mu+3\sigma] [μ−3σ,μ+3σ]的值视为正常值范围,在 [ μ − 3 σ , μ + 3 σ ] [\mu-3\sigma,\mu+3\sigma] [μ−3σ,μ+3σ]外的值视为离群值。
# 标准差法
import seaborn as sns
import numpy as np
def std_(df):
item, N = 'sepal_length', df.shape[0]
M = np.sum(df[item])/N
assert (M == np.mean(df[item])), 'mean is error'
S = np.sqrt(np.sum((df[item]-M)**2)/N)
L, R = M-3*S, M+3*S
return '正常区间值为 [%.4f, %.4f]' % (L, R)
df = sns.load_dataset('iris')
std_(df)
'正常区间值为 [3.3674, 8.3192]'
3.1.2.2.MAD法
概念:又称为绝对值差中位数法,是一种先需计算所有因子与中位数之间的距离总和来检测离群值的方法,适用大样本数据
公式:设有平稳离散数据X=[x1,x2,…,xn],其数据中位数 X m e d i a n X_{median} Xmedian;记
α = ∑ i = 1 n ( x i − x m e d i a n ) 2 n \alpha=\sqrt \frac{\sum_{i=1}^n(x_i-x_{median})^2}{n} α=n∑i=1n(xi−xmedian)2
则正常值范围为 [ x m e d i a n − 3 α , x m e d i a n + 3 α ] [x_{median}-3\alpha,x_{median}+3\alpha] [xmedian−3α,xmedian+3α],在区间 [ x m e d i a n − 3 α , x m e d i a n + 3 α ] [x_{median}-3\alpha,x_{median}+3\alpha] [xmedian−3α,xmedian+3α]外视为离群值
# MAD法
def MAD(df):
item, N = 'sepal_length', df.shape[0]
M = np.median(df[item])
A = np.sqrt(np.sum((df[item]-M)**2)/N)
L, R = M-3*A, M+3*A
return '正常区间值为 [%.4f, %.4f]' % (L, R)
MAD(df)
'正常区间值为 [3.3207, 8.2793]'
3.1.2.3.箱形图法
理论部分
概念:箱形图由最小值、下四分位值(25%),中位数(50%),上四分位数值(75%),
最大值这5个关键的百分数统计值组成的。
如何通过箱形图判断异常值呢?
假设下四分位值为 Q 1 Q1 Q1,上四分位数值为 Q 3 Q3 Q3,四分位距为 I Q R IQR IQR(其中 I Q R = Q 3 − Q 1 IQR=Q3-Q1 IQR=Q3−Q1),推导如下:
- 异常值截断点如下,截断点就是异常值与正常值的分界点,又称为内限:
[ Q 1 − 1.5 I Q R , Q 1 + 1.5 I Q R ] [Q1-1.5IQR,Q1+1.5IQR] [Q1−1.5IQR,Q1+1.5IQR] - 温和异常值与极端异常值的分界点,又称为外限:
[ Q 1 − 3 I Q R , Q 3 + 3 I Q R ] [Q1-3IQR,Q3+3IQR] [Q1−3IQR,Q3+3IQR] - 温和异常值:在内限与外限之间的值称为温和异常值,也就是说在对数据要求不是很严格的情况下,
这类异常值可以当成正常值要处理。 - 极端异常值:在外限以外的值称为极端异常值,可考虑直接删除处理或者处理成缺失值再进行填充。
import numpy as np
def boxplot(data):
# 下四分位数值、中位数,上四分位数值
Q1, median, Q3 = np.percentile(data, (25, 50, 75), interpolation='midpoint')
# 四分位距
IQR = Q3 - Q1
# 内限
inner = [Q1-1.5*IQR, Q3+1.5*IQR]
# 外限
outer = [Q1-3.0*IQR, Q3+3.0*IQR]
print('>>>内限:', inner)
print('>>>外限:', outer)
# 过滤掉极端异常值
print(len(data))
goodData = []
for value in data:
if (value < outer[1]) and (value > outer[0]):
goodData.append(value)
print(len(goodData))
return goodData
data = [0.2, 0.3, 0.15, 0.32, 1.5, 0.17, 0.28, 4.3, 0.8, 0.43, 0.67]
boxplot(data)
>>>内限: [-0.5025000000000002, 1.4775000000000003]
>>>外限: [-1.2450000000000003, 2.2200000000000006]
11
10
[0.2, 0.3, 0.15, 0.32, 1.5, 0.17, 0.28, 0.8, 0.43, 0.67]
3.1.2.4.图像对比法
概念和工作原理
所谓的图像对比法是通过比较训练集和测试集对应的特征数据在某一区间是否存在较大的差距来判别这一区间的数据是不是属于异常离群值。
优缺点
优点:可以防止训练集得到的模型不适合测试集预测的模型,从而减少二者之间的误差。
应用场景及意义
意义:提高模型的可靠性和稳定性。
功能实现
构造数据,进行实验演示方法原理的应用。
# 功能实现
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# 构造一个演示数据
D1 = {'feature1':[1,4,3,4,6.3,6,7,8,8.3,10,9.5,12,11.2,14.5,17.8,15.3,17.3,17,19,18.8],
'feature2':[11,20,38,40,59,61,77,84,99,115,123,134,130,155,138,160,152,160,189,234],
'label':[1,5,9,4,12,6,17,25,19,10,31,11,13,21,15,28,35,24,19,20]}
D2= {'feature1':[1,3,3,6,5,6,7,10,9,10,13,12,16,14,15,16,14,21,19,20],
'feature2':[13,25,33,49,45,66,74,86,92,119,127,21,13,44,34,29,168,174,178,230]}
df_train = pd.DataFrame(data=D1)
df_test = pd.DataFrame(data=D2)
L = [df_train.iloc[:,1], df_test.iloc[:,1], 'train_feature2', 'test_feature2']
fig = plt.figure(figsize=(15,5))
X = list(range(df_train.shape[0]))
for i in range(2):
ax = fig.add_subplot(1,2,i+1)
ax.plot(X, L[i],label=L[i+2],color='red')
ax.legend()
ax.set_xlabel('Section')

结论:
从上面的的图形对比,明显发现在区间 [10,15] 之间训练集 feature2 和测试集 feature2 的数据差距悬殊(严重突变),
因此区间 [10,15] 的数据可判定为离群异常值,应在训练集和测试集中同时剔除掉,防止训练集训练的模型不适用于测试集的预测。
如果不进行剔除或其他处理,训练模型在测试集预测会存在巨大的误差。
3.1.3 数据变换
已经归纳到特征构造当中,详细请看特征构造这一小节。
3.1.4.无量纲化
3.1.4.1.极差标准化(Min-nax)
Min-max区间缩放法(极差标准化),将数值缩放到[0 1]区间
X i ~ = x i − x m i n x m a x − x m i n \tilde{X_i}=\frac{x_i-x_{min}}{x_{max}-x_{min}} Xi~=xmax−xminxi−xmin
3.1.4.2.极大值标准化(Max-abs)
Max-abs (极大值标准化),标准化之后的每一维特征最大要素为1,其余要素均小于1,理论公式如下:
X i ~ = ∣ x i ∣ ∣ x m a x ∣ \tilde{X_i}=\frac{|x_i|}{|x_{max}|} Xi~=∣xmax∣∣xi∣
3.1.4.3.标准差标准化(z-score)
z-score 标准化(标准差标准化)为类似正态分布,均值为0,标准差为1
X i ~ = x i − μ σ , 其 中 均 值 为 μ = 1 n ∑ i = 0 n x i , 标 准 差 为 σ = ( x i − μ ) 2 n \tilde{X_i}=\frac{x_i-\mu}{\sigma},其中 均值为\mu=\frac{1}{n}\sum \limits_{i=0}^n x_i,标准差为\sigma=\sqrt \frac{(x_i-\mu)^2}{n} Xi~=σxi−μ,其中均值为μ=n1i=0∑nxi,标准差为σ=n(xi−μ)2
3.1.4.4.归一化——总和标准化
归一化(总和标准化),归一化的目的是将所有数据变换成和为1的数据,常用于权重的处理,在不同数据比较中,
常用到权重值来表示其重要性,往往也需要进行加权平均处理。
X i ~ = x i ∑ j = 1 n ∣ x j ∣ \tilde{X_i}=\frac{x_i}{\sum_{j=1}^n|x_j|} Xi~=∑j=1n∣xj∣xi
3.1.4.5.非线性归一化
非线性归一化:对于所属范围未知或者所属范围是全体实数,同时不服从正态分布的数据,
对其作Min-max标准化、z-score标准化或者归一化都是不合理的。
要使范围为R的数据映射到区间[0,1]内,需要作一个非线性映射。而常用的有sigmoid函数、arctan函数和tanh函数。
sigmoid函数 y = 1 1 + e − x y=\frac{1}{1+e^{-x}} y=1+e−x1
arctan函数 y = a r c t a n x y=arctanx y=arctanx
tanh函数 y = t a n h x = e x − e − x e x + e − x y=tanhx=\frac{e^x-e_{}^{-x}}{e^x+e^{-x}} y=tanhx=ex+e−xex−e−x
import seaborn as sns
import numpy as np
df = sns.load_dataset('iris')
print(df.shape)
df.head()
(150, 5)
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
# 1.Min-max 区间缩放法-极差标准化
# 自己手写理论公式来实现功能
# 缩放到区间 [0 1]
def Min_max(df):
x_minmax = []
for item in df.columns.tolist()[:4]:
MM = (df[item] - np.min(df[item]))/(np.max(df[item])-np.min(df[item]))
x_minmax.append(MM.values)
return np.array(np.matrix(x_minmax).T)[:5]
Min_max(df)
array([[0.22222222, 0.625 , 0.06779661, 0.04166667],
[0.16666667, 0.41666667, 0.06779661, 0.04166667],
[0.11111111, 0.5 , 0.05084746, 0.04166667],
[0.08333333, 0.45833333, 0.08474576, 0.04166667],
[0.19444444, 0.66666667, 0.06779661, 0.04166667]])
# 直接调用 sklearn 模块的 API 接口
# 极差标准化(最大最小值标准化)
from sklearn.preprocessing import MinMaxScaler
mms = MinMaxScaler()
x_minmax_scaler = mms.fit_transform(df.iloc[:, :4])
x_minmax_scaler[:5]
array([[0.22222222, 0.625 , 0.06779661, 0.04166667],
[0.16666667, 0.41666667, 0.06779661, 0.04166667],
[0.11111111, 0.5 , 0.05084746, 0.04166667],
[0.08333333, 0.45833333, 0.08474576, 0.04166667],
[0.19444444, 0.66666667, 0.06779661, 0.04166667]])
# 2.MaxAbs 极大值标准化
# 自己手写理论公式来实现功能
def MaxAbs(df):
x_maxabs_scaler = []
for item in df.columns.tolist()[:4]:
Max = np.abs(np.max(df[item]))
MA = np.abs(df[item])/Max
x_maxabs_scaler.append(MA)
return np.array(np.matrix(x_maxabs_scaler).T)[:5]
MaxAbs(df)
array([[0.64556962, 0.79545455, 0.20289855, 0.08 ],
[0.62025316, 0.68181818, 0.20289855, 0.08 ],
[0.59493671, 0.72727273, 0.1884058 , 0.08 ],
[0.58227848, 0.70454545, 0.2173913 , 0.08 ],
[0.63291139, 0.81818182, 0.20289855, 0.08 ]])
# 直接调用 sklearn 模块的 API 接口
# 极大值标准化
from sklearn.preprocessing import MaxAbsScaler
mas = MaxAbsScaler()
x_maxabs_scaler = mas.fit_transform(df.iloc[:, :4])
x_maxabs_scaler[:5]
array([[0.64556962, 0.79545455, 0.20289855, 0.08 ],
[0.62025316, 0.68181818, 0.20289855, 0.08 ],
[0.59493671, 0.72727273, 0.1884058 , 0.08 ],
[0.58227848, 0.70454545, 0.2173913 , 0.08 ],
[0.63291139, 0.81818182, 0.20289855, 0.08 ]])
# 3.z-score 标准差标准化
# 自己手写理论公式来实现功能
# 标准化之后均值为 0,标准差为 1
def z_score(df):
N, x_z = df.shape[0], []
for item in df.columns.tolist()[:4]:
mean = np.sum(df[item])/N
std = np.sqrt(np.sum((df[item]-mean)**2)/N)
Z = (df[item] - mean)/std
x_z.append(Z)
return np.array(np.matrix(x_z).T)[:5]
z_score(df)
array([[-0.90068117, 1.01900435, -1.34022653, -1.3154443 ],
[-1.14301691, -0.13197948, -1.34022653, -1.3154443 ],
[-1.38535265, 0.32841405, -1.39706395, -1.3154443 ],
[-1.50652052, 0.09821729, -1.2833891 , -1.3154443 ],
[-1.02184904, 1.24920112, -1.34022653, -1.3154443 ]])
# 直接调用 sklearn 模块的 API 接口
# 标准差标准化
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
x_std_scaler = ss.fit_transform(df.iloc[:, :4])
x_std_scaler[:5]
array([[-0.90068117, 1.01900435, -1.34022653, -1.3154443 ],
[-1.14301691, -0.13197948, -1.34022653, -1.3154443 ],
[-1.38535265, 0.32841405, -1.39706395, -1.3154443 ],
[-1.50652052, 0.09821729, -1.2833891 , -1.3154443 ],
[-1.02184904, 1.24920112, -1.34022653, -1.3154443 ]])
# 4.归一化---总和归一化
# 自己手写理论公式来实现功能
# 处理成所有数据和为1,权重处理
def feature_importance(df):
x_sum_scaler = []
for item in df.columns.tolist()[:4]:
S = np.sum(df[item])
FI = df[item]/S
x_sum_scaler.append(FI)
return np.array(np.matrix(x_sum_scaler).T)[:5]
feature_importance(df)
array([[0.0058186 , 0.00763192, 0.00248359, 0.00111173],
[0.00559042, 0.00654165, 0.00248359, 0.00111173],
[0.00536224, 0.00697776, 0.00230619, 0.00111173],
[0.00524815, 0.0067597 , 0.00266099, 0.00111173],
[0.00570451, 0.00784998, 0.00248359, 0.00111173]])
# 非线性归一化
# 自己手写理论公式来实现功能
# sigmoid 函数归一化
def sigmoid(df):
x_sigmoid = []
for item in df.columns.tolist()[:4]:
S = 1/(1+np.exp(-df[item]))
x_sigmoid.append(S)
return np.array(np.matrix(x_sigmoid).T)[:5]
sigmoid(df)
array([[0.9939402 , 0.97068777, 0.80218389, 0.549834 ],
[0.99260846, 0.95257413, 0.80218389, 0.549834 ],
[0.9909867 , 0.96083428, 0.78583498, 0.549834 ],
[0.9900482 , 0.95689275, 0.81757448, 0.549834 ],
[0.99330715, 0.97340301, 0.80218389, 0.549834 ]])
3.1.5.连续变量离散化(粗度)
连续变量离散化又可以归纳为粗细度调整的问题。
有些时候我们需要对数据进行粗粒度、细粒度划分,以便模型更好的学习到特征的信息,比如:
- 粗粒度划分(连续数据离散化):将年龄段0~100岁的连续数据进行粗粒度处理,也可称为二值化或离散化或分桶法
- 细粒度划分:在文本挖掘中,往往将段落或句子细分具体到一个词语或者字,这个过程称为细粒度划分
对于连续变量,为什么还需要进行离散化呢?
-推荐阅读为什么把连续数据离散化-参考资料
离散化有很多的好处,比如能够使我们的模型更加的简单、高效且低耗内存等优点,
因为相对于连续类型数据,离散类型数据的可能性更少。
离散化的通用流程如下:
(1)对此特征进行排序。特别是对于大数据集,排序算法的选择要有助于节省时间,
提高效率,减少离散化的整个过程的时间开支及复杂度。
(2)选择某个点作为候选断点,用所选取的具体的离散化方法的尺度进行衡量此候选断点是否满足要求。
(3)若候选断点满足离散化的衡量尺度,则对数据集进行分裂或合并,再选择下一个候选断点,重复步骤(2)(3)。
(4)当离散算法存在停止准则时,如果满足停止准则,则不再进行离散化过程,从而得到最终的离散结果。
3.1.5.1.特征二值化
思想:设定一个划分的阈值,当数值大于设定的阈值时,就赋值为1,;反之赋值为0。
(提示:赋值的值可以根据实际需要来自定义设定)
X = { 1 , X > t h r e s h o l d ( 阈 值 ) 0 , X ≤ t h r e s h o l d ( 阈 值 ) X =\left\{\begin{aligned}1&,& \ \ X>threshold(阈值)\\0&,& X\leq threshold(阈值)\end{aligned}\right. X={10,, X>threshold(阈值)X≤threshold(阈值)
典例(年龄粗划分):
X = { 0 , X ϵ [ 0 , 18 ] 岁 1 , X ϵ [ 19 , 40 ] 岁 2 , X ϵ [ 41 , 60 ] 岁 X=\left\{\begin{aligned}0&,& \ \ X\epsilon[0,18]岁\\1&,& X\epsilon[19, 40]岁\\ 2&,& X\epsilon[41, 60]岁\end{aligned}\right. X=⎩⎪⎨⎪⎧012,,, Xϵ[0,18]岁Xϵ[19,40]岁Xϵ[41,60]岁
# 特征二值化
# 自己手写理论公式来实现功能
def Binarizer(ages):
ages_binarizer = []
print('>>>原始的定量数据\n', ages)
for age in ages:
if (age > 0) and (age <= 18):
ages_binarizer.append(0)
elif (age >= 19) and (age <= 40):
ages_binarizer.append(1)
elif (age >= 41) and (age <= 60):
ages_binarizer.append(2)
print('\n>>>特征二值化之后的定性数据\n', ages_binarizer)
return ages_binarizer
ages = [4, 6, 56, 48, 10, 12, 15, 26, 20, 30, 34, 23, 38, 45, 41, 18]
Binarizer(ages)
>>>原始的定量数据
[4, 6, 56, 48, 10, 12, 15, 26, 20, 30, 34, 23, 38, 45, 41, 18]
>>>特征二值化之后的定性数据
[0, 0, 2, 2, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 0]
[0, 0, 2, 2, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 0]
# 直接调用 sklearn 模块的 API 接口
# binary 二值化
# 使用上面的 IRIS 数据集
from sklearn.preprocessing import Binarizer
# 阈值自定义为 3.0
# 大于阈值映射为 1,反之为 0
b = Binarizer(threshold=3.0)
x_binarizer = b.fit_transform(df.iloc[:, :4])
x_binarizer[:5]
array([[1., 1., 0., 0.],
[1., 0., 0., 0.],
[1., 1., 0., 0.],
[1., 1., 0., 0.],
[1., 1., 0., 0.]])
3.1.5.2.无监督离散化
概念及工作原理
(一)分箱法
分箱法又分为等宽(宽度)分箱法和等频(频数)分箱法,它们的概念介绍如下:
- 等宽分箱法(基于属性/特征值大小区间来划分):按照相同宽度将数据分成几等份。
- 等频分箱法(基于样本数量区间来划分):将数据分成几等份,每等份数据里面的个数(数量/频数)是一样的。
(二)聚类划分
聚类划分:使用聚类算法将数据聚成几类,每一个类为一个划分。
理论公式及推导
设有一维特征 X = [ x 1 , x 2 , . . . , x n ] X=[x1, x2,...,xn] X=[x1,x2,...,xn],理论假设如下:
(1)等宽分箱法:
假设 X 的最小值 x m i x = 0 x_{mix}=0 xmix=0,最大值 x m a x = 80 x_{max}=80 xmax=80,那么按照等宽分箱法定义
可以将 X 划分成 4 等份,其区间划分为[0, 20], [21, 40], [41, 60], [61, 80],每一个区间对应着一个离散值。
推广通用理论(请注意:为了方便计算,k 从 1 开始,而不是从 0 开始):
设 X 属性值的 x m i n = a , x m a x = b x_{min}=a, x_{max}=b xmin=a,xmax=b,将连续数据按照等宽法定义离散为 k k k 等份,则:
离散值为 v a l u e = [ 1 , 2 , 3 , . . . , k ] value=[1,2,3,...,k] value=[1,2,3,...,k]
划分属性值宽度为 w i d t h = ( b − a ) / k width = (b-a)/k width=(b−a)/k
那么划分区间为 k 等份,每个区间对应着一个离散值 [ [ a , a + w i d t h ] [ a + w i d t h , a + 2 ∗ w i d t h ] . . . . . . . . . [ a + ( k − 1 ) ∗ w i d t h , a + k ∗ w i d t h ] ] ⇒ [ v a l u e ( 1 ) v a l u e ( 2 ) . . . v a l u e ( k ) ] , 其 中 b = a + k ∗ w i d t h \begin{bmatrix} [a, a+width]\\ [a+width, a+2*width]\\ ...\\ ...\\ ...\\ [a+(k-1)*width, a+k*width]\end{bmatrix} \Rightarrow \begin{bmatrix} value(1)\\ value(2)\\ .\\ .\\ .\\ value(k) \end{bmatrix} ,其中 b=a+k*width ⎣⎢⎢⎢⎢⎢⎢⎡[a,a+width][a+width,a+2∗width].........[a+(k−1)∗width,a+k∗width]⎦⎥⎥⎥⎥⎥⎥⎤⇒⎣⎢⎢⎢⎢⎢⎢⎡value(1)value(2)...value(k)⎦⎥⎥⎥⎥⎥⎥⎤,其中b=a+k∗width
详细原理实现请参见代码实现部分
(2)等频分箱法:
假设 X 的样本数量有 80 个,那么按照等频分箱法定义,可以划分为 4 等份,每 20 个样本划分为 1 等份。
(3)聚类划分:
使用 K-Means 聚类算法进行无监督划分为 k 等份。
优缺点
无监督的方法的缺陷在于它对分布不均匀的数据不适用,对异常点比较敏感。
# 等宽分箱法
# 自己手写理论公式来实现功能
def equal_width_box(data):
# 划分的等份数、储存等宽分箱离散后的数据
k, data_width_box = 3, data
# 分箱的宽度、区间起始值(最小值)、离散值
width, start, value = (max(data)-min(data))/k, min(data), list(range(1, k+1))
for i in range(1, k+1):
# 实现公式 [a+(k−1)∗width, a+k∗width]
left = start+(i-1)*width # 左区间
right = start+(i*width) # 右区间
print('第 %d 个区间:[%.2f, %.2f]'%(i, left, right))
for j in range(len(data)):
if (data[j] >= left) and (data[j] <= right): # 判断是否属于 value[i] 区间
data_width_box[j] = value[i-1]
return data_width_box
data = [4, 6, 56, 48, 10, 12, 15, 26, 20, 30, 34, 23, 38, 45, 41, 18]
equal_width_box(data)
第 1 个区间:[4.00, 21.33]
第 2 个区间:[21.33, 38.67]
第 3 个区间:[38.67, 56.00]
[1, 1, 3, 3, 1, 1, 1, 2, 1, 2, 2, 2, 2, 3, 3, 1]
# 聚类划分
import seaborn as sns
import numpy as np
from sklearn.cluster import KMeans
data = sns.load_dataset('iris')
X = data.iloc[:,1]
kmeans = KMeans(n_clusters=4) # 离散为 4 等份
kmeans.fit_transform(np.array(X).reshape(-1, 1)) # 只取一个特征进行聚类离散化
print('>>>原始数据:', X.tolist())
print('>>>聚类离散后:', kmeans.labels_)
>>>原始数据: [3.5, 3.0, 3.2, 3.1, 3.6, 3.9, 3.4, 3.4, 2.9, 3.1, 3.7, 3.4, 3.0, 3.0, 4.0, 4.4, 3.9, 3.5, 3.8, 3.8, 3.4, 3.7, 3.6, 3.3, 3.4, 3.0, 3.4, 3.5, 3.4, 3.2, 3.1, 3.4, 4.1, 4.2, 3.1, 3.2, 3.5, 3.6, 3.0, 3.4, 3.5, 2.3, 3.2, 3.5, 3.8, 3.0, 3.8, 3.2, 3.7, 3.3, 3.2, 3.2, 3.1, 2.3, 2.8, 2.8, 3.3, 2.4, 2.9, 2.7, 2.0, 3.0, 2.2, 2.9, 2.9, 3.1, 3.0, 2.7, 2.2, 2.5, 3.2, 2.8, 2.5, 2.8, 2.9, 3.0, 2.8, 3.0, 2.9, 2.6, 2.4, 2.4, 2.7, 2.7, 3.0, 3.4, 3.1, 2.3, 3.0, 2.5, 2.6, 3.0, 2.6, 2.3, 2.7, 3.0, 2.9, 2.9, 2.5, 2.8, 3.3, 2.7, 3.0, 2.9, 3.0, 3.0, 2.5, 2.9, 2.5, 3.6, 3.2, 2.7, 3.0, 2.5, 2.8, 3.2, 3.0, 3.8, 2.6, 2.2, 3.2, 2.8, 2.8, 2.7, 3.3, 3.2, 2.8, 3.0, 2.8, 3.0, 2.8, 3.8, 2.8, 2.8, 2.6, 3.0, 3.4, 3.1, 3.0, 3.1, 3.1, 3.1, 2.7, 3.2, 3.3, 3.0, 2.5, 3.0, 3.4, 3.0]
>>>聚类离散后: [2 0 2 0 2 1 2 2 0 0 1 2 0 0 1 1 1 2 1 1 2 1 2 2 2 0 2 2 2 2 0 2 1 1 0 2 2
2 0 2 2 3 2 2 1 0 1 2 1 2 2 2 0 3 0 0 2 3 0 0 3 0 3 0 0 0 0 0 3 3 2 0 3 0
0 0 0 0 0 3 3 3 0 0 0 2 0 3 0 3 3 0 3 3 0 0 0 0 3 0 2 0 0 0 0 0 3 0 3 2 2
0 0 3 0 2 0 1 3 3 2 0 0 0 2 2 0 0 0 0 0 1 0 0 3 0 2 0 0 0 0 0 0 2 2 0 3 0
2 0]
3.1.6 类别数据处理
很多算法模型不能直接处理字符串数据,因此需要将类别型数据转换成数值型数据
3.1.6.1.序号编码(Ordinal Encoding)
通常用来处理类别间具有大小关系的数据,比如成绩(高中低)
假设有类别数据X=[x1,x2,…,xn],则序号编码思想如下:
- (1)确定X中唯一值的个数K,将唯一值作为关键字,即Key=[x1,x2,…,xk]
- (2)生成k个数字作为键值,即Value=[0,1,2,…,k]
- (3)每一个唯一的类别型元素对应着一个数字,即键值对dict={key1:0, key2:1,…, keyk:k}
# 序号编码
# 自己手写理论公式实现功能(可优化)
import seaborn as sns
def LabelEncoding(df):
x, dfc = 'species', df
key = dfc[x].unique() # 将唯一值作为关键字
value = [i for i in range(len(key))] # 键值
Dict = dict(zip(key, value)) # 字典,即键值对
for i in range(len(key)):
for j in range(dfc.shape[0]):
if key[i] == dfc[x][j]:
dfc[x][j] = Dict[key[i]]
dfc[x] = dfc[x].astype(np.float32)
return dfc[:5]
data = sns.load_dataset('iris')
le = LabelEncoding(data)
le
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0.0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0.0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0.0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 0.0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 0.0 |
# 调用 sklearn 模块的 API 接口
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
x_le = le.fit_transform(data['species'])
x_le
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
3.1.6.2.独热编码(One-hot Encoding)
通常用于处理类别间不具有大小关系的特征,比如血型(A型血、B型血、AB型血、O型血),
独热编码会把血型变成一个稀疏向量,A型血表示为(1,0,0,0),B型血表示为(0,1,0,0),
AB型血表示为(0,0,1,0),O型血表示为(0,0,0,1)
提示
(1)在独热编码下,特征向量只有某一维取值为1,其余值均为0,因此可以利用向量的稀疏来节省空间
(2)如果类别型的唯一类别元素较多,可能会造成维度灾难,因此需要利用特征选择来降低维度。
假设有类别数据X=[x1,x2,…,xn],则独热编码思想如下:
- (1)确定X中唯一值的个数K,将唯一值作为关键字,即Key=[x1,x2,…,xk]
- (2)生成k个数字为1的一维数组作为键值,即Value=[1,1,1,…,k]
- (3)每一个唯一的类别型元素对应着一个数字,即键值对dict={key1:0, key2:1,…, keyk:k}
- (4)创建一个空的数组v=V(n维 x k维)=np.zeros((n, k))
- (5)将数值对应的那一维为1,其余为0,最后将V与原始数据合并即可
# 独热编码
# 自己手写理论实现功能
import seaborn as sns
import pandas as pd
import numpy as np
def OneHotEncoding(df):
x, dfc = 'species', df.copy()
key = dfc[x].unique() # (1)
value = np.ones(len(key)) # (2)
Dict = dict(zip(key, value)) # (3)
v = np.zeros((dfc.shape[0], len(key))) # (4)
for i in range(len(key)):
for j in range(dfc.shape[0]):
if key[i] == dfc[x][j]:
v[j][i] = Dict[key[i]] # (5)
dfv = pd.DataFrame(data=v, columns=['species_'] + key)
return pd.concat([dfc, dfv], axis=1)
data = sns.load_dataset('iris')
ohe = OneHotEncoding(data)
ohe.head()
| sepal_length | sepal_width | petal_length | petal_width | species | species_setosa | species_versicolor | species_virginica | |
|---|---|---|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa | 1.0 | 0.0 | 0.0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa | 1.0 | 0.0 | 0.0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa | 1.0 | 0.0 | 0.0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa | 1.0 | 0.0 | 0.0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa | 1.0 | 0.0 | 0.0 |
# 调用 sklearn 模块的 API 接口
# 注意要先序号编码再独热哑编码
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import LabelEncoder
def string_strip(x):
return x.strip() # 去除字符串周围的特殊字符(如:逗号、空格等)
ohe_data = np.array(list(map(string_strip, data['species'].tolist())))
le = LabelEncoder()
ohe = OneHotEncoder()
x_le = le.fit_transform(ohe_data)
x_ohe = ohe.fit_transform(x_le.reshape(-1,1)).toarray()
x_ohe[:5]
array([[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.]])
3.1.6.3.二进制编码(Binary Encoding)
二进制编码主要分为两步,先用序号编码给每个类别赋予一个类别ID,然后将类别ID对应的二进制编码作为结果。
以A、B、AB、O血型为例,表1.1是二进制编码的过程。
A型血的ID为1,二进制表示为001;B型血的ID为2,二进制表示为010;
以此类推可以得到AB型血和O型血的二进制表示。
可以看出,二进制编码本质上是利用二进制对ID进行哈希映射,
最终得到0/1特征向量,且维数少于独热编码,节省了存储空间。
3.1.7.数据集成
3.1.8.重复数据处理
3.1.9 数值与字符串转换问题
有时候,在数据预处理过程中,在确认代码不会出错的情况下,常常出现以下bug:
- 在某一列特征全部为数值的情况下,却出现"float不能转换成string"的 bug
- 在某一列特征全部为字符串的情况下如(“13”),却出现"string不能转换成float"的 bug
这两种情况都说明,某一列特征数据并不纯净,而是含有一些特征的字符(如:空格、换行符、逗号、句号等),
因此在进行其他操作之前要写个正则表达式或者try…except…进行赋值处理等。
3.2.非结构化数据预处理
3.2.1.文本数据处理
3.2.2.图像数据处理
4.特征构造
1. 概念及工作原理
概念:特征构造主要是产生衍生变量,所谓衍生变量是指对原始数据进行加工、特征组合,生成有商业意义的新变量(新特征)
2. 别称
特征构造也可称为特征交叉、特征组合、数据变换
3. 优缺点
**优点:**新构造的有效且合理的特征可提高模型的预测表现能力。
缺点:
(1)新构造的特征不一定是对模型有正向影响作用的,也许对模型来说是没有影响的甚至是负向影响,拉低模型的性能。
(2)因此构造的新特征需要反复参与模型进行训练验证或者进行特征选择之后,才能确认特征是否是有意义的。
4.1.特征设计原理
特征构造一些理论
新特征设计应与目标高度相关,要考虑的问题:
- 这个特征是否对目标有实际意义?
- 如果有用,这个特征重要性如何?
- 这个特征的信息是否在其他特征上体现过?
新构建特征验证其有效性要考虑的问题:
- 需要领域知识、直觉、行业经验以及数学知识综合性考量特征的有效性,防止胡乱构造没有意义的特征。
- 要反复与模型进行迭代验证其是否对模型有正向促进作用。
- 或者进行特征选择判定新构建特征的重要性来衡量其有效性。
4.2.特征构造常用方法
下面介绍一些常用的案例方法,作为特征构造的参考方向。特征构造需要根据具体的问题
构造出与目标高度相关的新特征,如此一来说明特征构造是有点难度的。需要不断结合具体业务
情况做出合理分析,才能有根据性的构造出有用的新特征。
4.2.1.统计值构造法
概念及工作原理
概念:指通过统计单个或者多个变量的统计值(max,min,count,mean)等而形成新的特征。
单变量:
如果某个特征与目标高度相关,那么可以根据具体的情况取这个特征的统计值作为新的特征。
多变量:
如果特征与特征之间存在交互影响时,那么可以聚合分组两个或多个变量之后,再以统计值构造出新的特征。
# ------------------------------------
# 代码实现功能
# ------------------------------------
import seaborn as sns
import numpy as np
import pandas as pd
import warnings
from sklearn.preprocessing import LabelEncoder
warnings.filterwarnings('ignore')
df = sns.load_dataset('iris')
le = LabelEncoder()
df['species'] = le.fit_transform(df['species'])
df = df.rename(columns={'species':'labels'})
df = df[['labels', 'sepal_length', 'sepal_width', 'petal_length', 'petal_width']]
print(df.shape)
df.head()
(150, 5)
| labels | sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|---|
| 0 | 0 | 5.1 | 3.5 | 1.4 | 0.2 |
| 1 | 0 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 0 | 4.7 | 3.2 | 1.3 | 0.2 |
| 3 | 0 | 4.6 | 3.1 | 1.5 | 0.2 |
| 4 | 0 | 5.0 | 3.6 | 1.4 | 0.2 |
# 单变量
# 计数特征
# 简单示例:统计单个变量数值次数作为新的特征
newF1 = df.groupby(['petal_width'])['petal_width'].count().to_frame().rename(columns={'petal_width':'petal_width_count'}).reset_index()
df_newF1 = pd.merge(df, newF1, on=['petal_width'], how='inner')
print('>>>新构建的计数特征的唯一值数据:\n', df_newF1['petal_width_count'].unique())
df_newF1.head()
>>>新构建的计数特征的唯一值数据:
[29 7 5 1 8 12 13 4 3 2 6]
| labels | sepal_length | sepal_width | petal_length | petal_width | petal_width_count | |
|---|---|---|---|---|---|---|
| 0 | 0 | 5.1 | 3.5 | 1.4 | 0.2 | 29 |
| 1 | 0 | 4.9 | 3.0 | 1.4 | 0.2 | 29 |
| 2 | 0 | 4.7 | 3.2 | 1.3 | 0.2 | 29 |
| 3 | 0 | 4.6 | 3.1 | 1.5 | 0.2 | 29 |
| 4 | 0 | 5.0 | 3.6 | 1.4 | 0.2 | 29 |
就这样,我们构造出一个新的特征 petal_width_count
# 多变量
name = {'count': 'petal_width_count', 'min':'petal_width_min',
'max':'petal_width_max', 'mean':'petal_width_mean',
'std':'petal_width_std'}
newF2 = df.groupby(by=['sepal_length'])['petal_width'].agg(['count', 'min', 'max', 'mean', 'std']).rename(columns=name).reset_index()
df_newF2 = pd.merge(df, newF2, on='sepal_length', how='inner')
# 由于聚合分组之后有一些样本的 std 会存在缺失值,所以统一填充为 0
df_newF2['petal_width_std'] = df_newF2['petal_width_std'].fillna(0)
df_newF2.head()
# df_newF2.columns.tolist()
| labels | sepal_length | sepal_width | petal_length | petal_width | petal_width_count | petal_width_min | petal_width_max | petal_width_mean | petal_width_std | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 5.1 | 3.5 | 1.4 | 0.2 | 9 | 0.2 | 1.1 | 0.4 | 0.282843 |
| 1 | 0 | 5.1 | 3.5 | 1.4 | 0.3 | 9 | 0.2 | 1.1 | 0.4 | 0.282843 |
| 2 | 0 | 5.1 | 3.8 | 1.5 | 0.3 | 9 | 0.2 | 1.1 | 0.4 | 0.282843 |
| 3 | 0 | 5.1 | 3.7 | 1.5 | 0.4 | 9 | 0.2 | 1.1 | 0.4 | 0.282843 |
| 4 | 0 | 5.1 | 3.3 | 1.7 | 0.5 | 9 | 0.2 | 1.1 | 0.4 | 0.282843 |
就这样,我们基于两个变量聚合分组之后,使用统计值构建出 5 个新的特征,下面简单地来
验证演示一下新构造特征的有效性如何?
df_newF2.corr()
| labels | sepal_length | sepal_width | petal_length | petal_width | petal_width_count | petal_width_min | petal_width_max | petal_width_mean | petal_width_std | |
|---|---|---|---|---|---|---|---|---|---|---|
| labels | 1.000000 | 0.782561 | -0.426658 | 0.949035 | 0.956547 | -0.130436 | 0.761157 | 0.746428 | 0.840121 | 0.084261 |
| sepal_length | 0.782561 | 1.000000 | -0.117570 | 0.871754 | 0.817941 | -0.239228 | 0.904923 | 0.785504 | 0.929920 | -0.010766 |
| sepal_width | -0.426658 | -0.117570 | 1.000000 | -0.428440 | -0.366126 | -0.005658 | -0.173425 | -0.199324 | -0.240381 | -0.042336 |
| petal_length | 0.949035 | 0.871754 | -0.428440 | 1.000000 | 0.962865 | -0.171507 | 0.841046 | 0.782412 | 0.903936 | 0.039066 |
| petal_width | 0.956547 | 0.817941 | -0.366126 | 0.962865 | 1.000000 | -0.118262 | 0.798626 | 0.779989 | 0.879583 | 0.085073 |
| petal_width_count | -0.130436 | -0.239228 | -0.005658 | -0.171507 | -0.118262 | 1.000000 | -0.324154 | 0.142429 | -0.134452 | 0.459435 |
| petal_width_min | 0.761157 | 0.904923 | -0.173425 | 0.841046 | 0.798626 | -0.324154 | 1.000000 | 0.671591 | 0.907960 | -0.266577 |
| petal_width_max | 0.746428 | 0.785504 | -0.199324 | 0.782412 | 0.779989 | 0.142429 | 0.671591 | 1.000000 | 0.886771 | 0.504145 |
| petal_width_mean | 0.840121 | 0.929920 | -0.240381 | 0.903936 | 0.879583 | -0.134452 | 0.907960 | 0.886771 | 1.000000 | 0.096720 |
| petal_width_std | 0.084261 | -0.010766 | -0.042336 | 0.039066 | 0.085073 | 0.459435 | -0.266577 | 0.504145 | 0.096720 | 1.000000 |
通过上面的相关系数表可以发现,新构建的 5 个特征,除了 count、std 之外,其余 3 个特征跟目标相关性系数较高,
可以初步认为这 3 个特征是有实际意义的特征,下面进行模型训练简单验证一下。
from sklearn.svm import SVC
# 原数据特征表征能力
original_feature = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
X, Y = df_newF2[original_feature] , df_newF2['labels']
svc = SVC()
svc.fit(X,Y)
print('>>>原数据特征的表征能力得分:%.4f'%(svc.score(X,Y)), '\n')
# 单个新特征对应的表征能力
# 新特征的表征能力大小与其对应目标之间高度相关系数成正比
# 比如 mean 对应 labels 相关系数最大,所训练得出的 score 也是最大的
new_feature_test = ['petal_width_count', 'petal_width_min', 'petal_width_max', 'petal_width_mean', 'petal_width_std']
for col in new_feature_test:
X, Y = df_newF2[[col]] , df_newF2['labels']
svc = SVC()
svc.fit(X,Y)
print('>>>新特征 %s 的表征能力得分:%.4f'%(col, svc.score(X,Y)))
# 多个新特征组合对应的表征能力
print()
for col2 in new_feature_test:
merge_feature = original_feature + [col2]
X, Y = df_newF2[merge_feature] , df_newF2['labels']
svc = SVC()
svc.fit(X,Y)
print('>>>原始特征组合新特征 %s 的表征能力得分:%.4f'%(col2, svc.score(X,Y)))
>>>原数据特征的表征能力得分:0.9867
>>>新特征 petal_width_count 的表征能力得分:0.5067
>>>新特征 petal_width_min 的表征能力得分:0.6867
>>>新特征 petal_width_max 的表征能力得分:0.6600
>>>新特征 petal_width_mean 的表征能力得分:0.7600
>>>新特征 petal_width_std 的表征能力得分:0.3467
>>>原始特征组合新特征 petal_width_count 的表征能力得分:0.9600
>>>原始特征组合新特征 petal_width_min 的表征能力得分:0.9867
>>>原始特征组合新特征 petal_width_max 的表征能力得分:0.9800
>>>原始特征组合新特征 petal_width_mean 的表征能力得分:0.9867
>>>原始特征组合新特征 petal_width_std 的表征能力得分:0.9867
通过上面简单演示,可以知道在构造新特征之后类似于上面模型训练的方式来验证
新特征的表征能力以及有效性。当然,上面的验证方式只是简单的演示,具体且更标准
的验证方法可以自己去尝试。
4.2.2.连续数据离散化
这里不再重复描述,可参照数据预处理那一块内容。
一般可对年龄、收入等连续数据进行离散化。
优缺点:
优点:(1)降低数据的复杂性 (2)可在一定程度上消除多余的噪声
4.2.3.离散数据编码化
这里不再重复描述,可参照数据预处理那一块内容。
常用方法有序号编码、独热编码和二进制编码。
优缺点:
优点:(1)有些模型不支持离散字符串数据,离散编码便于模型学习
4.2.4.函数变换法
1. 概念及工作原理
简单常用的函数变换法(一般针对于连续数据):
(1)平方(小数值—>大数值)
(2)开平方(大数值—>小数值)
(3)指数
(4)对数
(5)差分
2. 理论公式及推导
平方 X = x 2 X=x^2 X=x2
开平方 X = x X=\sqrt x X=x
指数 X = e x X=e^x X=ex
对数 X = l o g x X=logx X=logx
多项式 X = 1 + x + x 2 + x 3 + . . . + x n X=1+x+x^2+x^3+...+x^n X=1+x+x2+x3+...+xn
差分 X = x i + 1 − x i X=x_{i+1}-x_{i} X=xi+1−xi
为什么要对时间序列数据进行差分?
首先来看下为什么要对数据进行差分变化,差分变化可以消除数据对时间的依赖性,
也就是降低时间对数据的影响,这些影响通常包括数据的变化趋势以及数据周期性变化的规律。进行差分操作时,
一般用现在的观测值减去上个时刻的值就得到差分结果,就是这么简单,按照这种定义可以计算一系列的差分变换。
3. 优缺点
优点:
(1)将不具有正态分布的数据变换成具有正态分布的数据
(2)对于时间序列分析,有时简单的对数变换和差分运算就可以将非平稳序列转换成平稳序列
4. 应用场景及意义
应用场景:(1)数据不呈正态分布时可运用 (2)当前特征数据不利于被模型捕获利用
5. 功能实现
代码实现如下
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
X = np.array([[0,1,2],
[3,4,5],
[6,7,8]])
X1 = X**2
print('>>>平方\n', X1)
X2 = np.sqrt(X)
print('>>>开平方\n', X2)
X3 = np.exp(X)
print('>>>指数\n', X3)
X4 = np.log(X)
print('>>>对数\n', X4)
>>>平方
[[ 0 1 4]
[ 9 16 25]
[36 49 64]]
>>>开平方
[[0. 1. 1.41421356]
[1.73205081 2. 2.23606798]
[2.44948974 2.64575131 2.82842712]]
>>>指数
[[1.00000000e+00 2.71828183e+00 7.38905610e+00]
[2.00855369e+01 5.45981500e+01 1.48413159e+02]
[4.03428793e+02 1.09663316e+03 2.98095799e+03]]
>>>对数
[[ -inf 0. 0.69314718]
[1.09861229 1.38629436 1.60943791]
[1.79175947 1.94591015 2.07944154]]
# 时间序列常用方法
# 非平稳序列转换成平稳序列
# 对数&差分
y = np.array([1.3, 5.5, 3.3, 5.3, 3.4, 8.0, 6.6, 8.7, 6.8, 7.9])
x = list(range(1, y.shape[0]+1))
# 假设这是一个时间序列图
plt.plot(x,y)
plt.title('original plot')
plt.xlabel('time')
Text(0.5, 0, 'time')

y_log = np.log(y)
# 假设这是一个时间序列图
plt.plot(x,y_log)
plt.title('log plot')
plt.xlabel('time')
Text(0.5, 0, 'time')
def diff(dataset):
DIFF = []
# 由于差分之后的数据比原数据少一个
DIFF.append(dataset[0])
for i in range(1, dataset.shape[0]): # 1 次差分
value = dataset[i] - dataset[i-1]
DIFF.append(value)
for i in range(1, dataset.shape[0]): # 2 次差分
value = DIFF[i] - DIFF[i-1]
DIFF.append(value)
x = list(range(1, len(DIFF)+1))
plt.plot(x,DIFF)
plt.title('biff after')
plt.xlabel('time')
return DIFF
DIFF = diff(y)
从上面图像发现经过对数变换的数据明显比差分变换的效果更好,对数变换后的数据更加的平稳。
以后可以根据具体情况使用不同方法处理。
# 多项式
from sklearn.preprocessing import PolynomialFeatures
print('>>>原始数据\n', X)
ploy1 = PolynomialFeatures(1)
print('>>>1 次项\n', ploy1.fit_transform(X))
ploy2 = PolynomialFeatures(2)
print('>>>2 次项\n', ploy2.fit_transform(X))
ploy3 = PolynomialFeatures(3)
print('>>>3 次项\n', ploy3.fit_transform(X))
# 1,x1,x2,x3
>>>原始数据
[[0 1 2]
[3 4 5]
[6 7 8]]
>>>1 次项
[[1. 0. 1. 2.]
[1. 3. 4. 5.]
[1. 6. 7. 8.]]
>>>2 次项
[[ 1. 0. 1. 2. 0. 0. 0. 1. 2. 4.]
[ 1. 3. 4. 5. 9. 12. 15. 16. 20. 25.]
[ 1. 6. 7. 8. 36. 42. 48. 49. 56. 64.]]
>>>3 次项
[[ 1. 0. 1. 2. 0. 0. 0. 1. 2. 4. 0. 0. 0. 0.
0. 0. 1. 2. 4. 8.]
[ 1. 3. 4. 5. 9. 12. 15. 16. 20. 25. 27. 36. 45. 48.
60. 75. 64. 80. 100. 125.]
[ 1. 6. 7. 8. 36. 42. 48. 49. 56. 64. 216. 252. 288. 294.
336. 384. 343. 392. 448. 512.]]
4.2.5.算术运算构造法
概念及工作原理
概念:根据实际情况需要,结合与目标相关性预期较高的情况下,由原始特征进行算数运算而形成新的特征。
解读概念为几种情况:
(1)原始单一特征进行算术运算:类似于无量纲那样处理,比如:X/max(X), X+10等
(2)特征之间进行算术运算:X(featureA)/X(featureB),X(featureA)-X(featureB)等
4.2.6.自由发挥
在特征构造这一块是没有什么明文规定的方法,特征构造更多的是结合实际情况,
有针对性的构造与目标高度相关的特征,只要构造的新特征能够解释模型和对模型具有
促进作用,都可以作为新指标新特征。
5.特征选择
5.1.特征选择概述
概念及工作原理
-
从哪些方面来选择特征呢?
当数据处理好之后,我们需要选择有意义的特征输入机器学习的模型进行训练,通常来说
要从两个方面考虑来选择特征,如下:
(1)特征是否发散
如果一个特征不发散,例如方差接近于0,也就是说样本在这个特征上基本上没有差异,这个特征对于样本的区分并没有什么用。
(2)特征与目标的相关性
这点比较显见,与目标相关性高的特征,应当优先选择。
区别:特征与特征之间相关性高的,应当优先去除掉其中一个特征,因为它们是替代品。 -
为什么要进行特征选择?
(1)减轻维数灾难问题
(2)降低学习任务的难度 -
处理高维数据的两大主流技术
特征选择和降维 -
特征选择有哪些方法呢?
(1)Filter 过滤法
(2)Wrapper 包装法
(3)Embedded 嵌入法
参考资料
-特征选择概述
# 加载 IRIS 数据集做演示
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.preprocessing import LabelEncoder
%matplotlib inline
df = sns.load_dataset('iris')
print(df.shape)
df['species'] = LabelEncoder().fit_transform(df.iloc[:, 4])
df.head()
(150, 5)
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 0 |
5.2.Filter 过滤法
它主要侧重于单个特征跟目标变量的相关性。
优点是计算时间上较高效,对于过拟合问题也具有较高的鲁棒性。
缺点就是倾向于选择冗余的特征,因为他们不考虑特征之间的相关性,有可能某一个特征的分类能力很差,
但是它和某些其它特征组合起来会得到不错的效果,这样就损失了有价值的特征。
5.2.1.方差选择法
为什么方差可以用于选择特征呢?
先从方差的概念说起,方差是衡量一个变量的离散程度(即数据偏离平均值的程度大小),
变量的方差越大,我们就可以认为它的离散程度越大,也就是意味着这个变量对模型的贡献和作用
会更明显,因此要保留方差较大的变量,反之,要剔除掉无意义的特征。
思路(先计算各个特征的方差,然后根据设定的阈值或待选择阈值的个数,选择方差大于阈值的特征),公式如下:
- (1)计算特征的方差。假设X=[x1,x2,…,xn],则方差为:
v a r ( X ) = 1 n − 1 ∑ i = 1 n ( x i − μ ) 2 , 其 中 μ 是 平 均 值 , 一 般 样 本 方 差 选 择 n − 1 较 好 var(X)=\frac{1}{n-1}\sum_{i=1}^n(x_i-\mu)^2,其中\mu是平均值,一般样本方差选择n-1较好 var(X)=n−11i=1∑n(xi−μ)2,其中μ是平均值,一般样本方差选择n−1较好 - (2)设定阈值,并筛选出大于阈值的特征或者筛选出待选择阈值的个数。
# 方差选择法
# 自己手写理论公式来实现功能
def VarianceThreshold(df, threshold=0.):
dfc = df.iloc[:, :4].copy()
print('>>>特征名:\n', dfc.columns.tolist())
# 1 求方差
var = np.sum(np.power(np.matrix(dfc.values)-np.matrix(dfc.mean()), 2), axis=0)/(dfc.shape[0]-1)
T = []
# 2 筛选大于阈值的特征
for index, v in enumerate(var.reshape(-1, 1)):
if v > threshold:
T.append(index)
dfc = dfc.iloc[:, T]
return var, dfc
# 阈值设置为 0.6
var, dfc = VarianceThreshold(df, 0.60)
print('\n>>>原始特征对应的方差值:\n', var)
print('\n>>>方差阈值选择后的特征名:\n', dfc.columns)
dfc.head()
>>>特征名:
['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
>>>原始特征对应的方差值:
[[0.68569351 0.18997942 3.11627785 0.58100626]]
>>>方差阈值选择后的特征名:
Index(['sepal_length', 'petal_length'], dtype='object')
| sepal_length | petal_length | |
|---|---|---|
| 0 | 5.1 | 1.4 |
| 1 | 4.9 | 1.4 |
| 2 | 4.7 | 1.3 |
| 3 | 4.6 | 1.5 |
| 4 | 5.0 | 1.4 |
# 调用 sklearn 模块 API 接口
from sklearn.feature_selection import VarianceThreshold
vt = VarianceThreshold(0.6)
x_vt = vt.fit_transform(df.iloc[:,:4])
print(vt.variances_)
x_vt[:5]
[0.68112222 0.18871289 3.09550267 0.57713289]
array([[5.1, 1.4],
[4.9, 1.4],
[4.7, 1.3],
[4.6, 1.5],
[5. , 1.4]])
5.2.2.相关系数法
第一种方法:计算特征与特征的相关系数
工作原理
通过计算特征与特征之间的相关系数的大小,可判定两两特征之间的相关程度。
取值区间在[-1, 1]之间,取值关系如下:
corr(x1,x2)相关系数值小于0表示负相关((这个变量下降,那个就会上升)),即x1与x2是互补特征
corr(x1,x2)相关系数值等于0表示无相关
corr(x1,x2)相关系数值大于0表示正相关,即x1与x2是替代特征
原理实现:取相关系数值的绝对值,然后把corr值大于90%~95%的两两特征中的某一个特征剔除。
如果两个特征是完全线性相关的,这个时候我们只需要保留其中一个即可。
因为第二个特征包含的信息完全被第一个特征所包含。
此时,如果两个特征同时都保留的话,模型的性能很大情况会出现下降的情况
理论公式及推导
假设X=[x1,x2,…,xn],其中x1,x2…是列向量,即x1代表一个特征,公式推导如下:
c o r r ( X 1 , X 2 ) = c o v ( X 1 , X 2 ) σ x 1 σ x 2 = ∑ i = 1 n ( x 1 i − μ x 1 ) ( x 2 i − μ x 2 ) ∑ i = 1 n ( x 1 i − μ x 1 ) 2 ∑ i = 1 n ( x 2 i − μ x 2 ) 2 , 其 中 μ 表 示 各 个 特 征 的 平 均 值 corr(X1,X2)=\frac{cov(X1,X2)}{\sigma_{x1}\sigma_{x2}}=\frac{\sum_{i=1}^n(x1_i-\mu_{x1})(x2_i-\mu_{x2})} {\sqrt{\sum_{i=1}^n(x1_i-\mu_{x1})^2}\sqrt{\sum_{i=1}^n(x2_i-\mu_{x2})^2}},其中\mu表示各个特征的平均值 corr(X1,X2)=σx1σx2cov(X1,X2)=∑i=1n(x1i−μx1)2∑i=1n(x2i−μx2)2∑i=1n(x1i−μx1)(x2i−μx2),其中μ表示各个特征的平均值
优缺点
优点:容易实现
缺点:只是根据特征与特征之间的相关度来筛选特征,但并没有结合与目标的相关度来衡量
应用场景
用于特征选择,以提取最有效的特征作为目标,剔除冗余特征
# 相关系数--特征与特征
# 自己手写理论公式实现功能
def corr_selector(df):
dfc = df.copy().iloc[:,:4]
CORR = np.zeros((dfc.shape[1], dfc.shape[1]))
delete, save = [], []
for i in range(dfc.shape[1]):
if dfc.columns.tolist()[i] not in delete:
save.append(dfc.columns.tolist()[i])
for j in range(i+1, dfc.shape[1]):
# 计算特征与特征之间的相关系数
cov = np.sum((dfc.iloc[:,i]-dfc.iloc[:,i].mean()) * (df.iloc[:,j]-df.iloc[:,j].mean()))
std = np.sqrt(np.sum((df.iloc[:,i]-df.iloc[:,i].mean())**2)) * np.sqrt(np.sum((df.iloc[:,j]-df.iloc[:,j].mean())**2))
corr = cov/std
CORR[i][j] = corr
# 筛选掉高线性相关两两特征中的某一个特征
if (np.abs(corr) > 0.89) and (dfc.columns.tolist()[j] not in delete):
delete.append(dfc.columns.tolist()[j])
dfc_ = dfc[save].copy()
return CORR, dfc_
corr,dfc_ = corr_selector(df)
print(corr)
dfc_.head()
[[ 0. -0.11756978 0.87175378 0.81794113]
[ 0. 0. -0.4284401 -0.36612593]
[ 0. 0. 0. 0.96286543]
[ 0. 0. 0. 0. ]]
| sepal_length | sepal_width | petal_length | |
|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 |
| 1 | 4.9 | 3.0 | 1.4 |
| 2 | 4.7 | 3.2 | 1.3 |
| 3 | 4.6 | 3.1 | 1.5 |
| 4 | 5.0 | 3.6 | 1.4 |
第二种方法:计算特征与目标的相关系数以及P值
原理依据
scipy.stats.pearsonr(x, y)
输出:(r, p)
r:相关系数[-1,1]之间
p:相关系数显著性
相关性的强度确实是用相关系数的大小来衡量的,但相关大小的评价要以相关系数显著性的评价为前提
因此,要先检验相关系数的显著性,如果显著,证明相关系数有统计学意义,下一步再来看相关系数大小;
如果相关系数没有统计学意义,那意味着你研究求得的相关系数也许是抽样误差或者测量误差造成的,再进行一次研究结果可
能就大不一样,此时讨论相关性强弱的意义就大大减弱了。
原理实现:先计算各个特征对目标值的相关系数以及相关系数的P值
优缺点
Pearson相关系数的一个明显缺陷是,作为特征排序机制,他只对线性关系敏感。
如果关系是非线性的,即便两个变量具有一一对应的关系,Pearson相关性也可能会接近0
应用场景及意义
应用于回归问题的特征选择,旨在选择出最有效的信息和减少内存占用空间
# 相关系数--特征与目标变量
# 自己手写理论公式实现功能
def corr_selector(df):
X, y = df.iloc[:, :4], df.iloc[:, 4]
cor_list = []
for i in X.columns.tolist():
cor = np.corrcoef(X[i], y)[0, 1]
cor_list.append(cor)
print(X.columns.tolist())
print(cor_list)
return cor_list
corr_selector(df)
['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
[0.782561231810082, -0.4266575607811244, 0.9490346990083889, 0.9565473328764034]
[0.782561231810082,
-0.4266575607811244,
0.9490346990083889,
0.9565473328764034]
df.plot()
plt.savefig('corr.png')
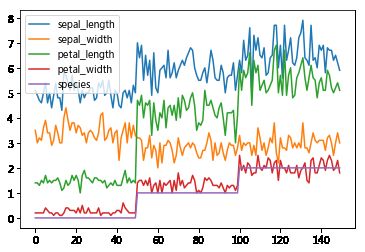
从图像趋势来看:
- petal_width、petal_length与目标变量species有着非常显著的相关性
- sepal_length与目标变量species有着较强的相关性
- sepal_width与目标变量species没有明显的相关性,sepal_width的数值在species各个类别中的数值几乎是不变的,因此它的贡献很小
从上面的方差选择法及自变量与应变量的相关系数法可以验证上面图像趋势分析的结论。
# 调用 sklearn 模块 API 接口
from sklearn.feature_selection import SelectKBest
from scipy.stats import pearsonr
from numpy import array
fun = lambda X, Y: tuple(map(tuple, array(list(map(lambda x: pearsonr(x, Y), X.T))).T))
sb = SelectKBest(fun, k=2)
x_sb = sb.fit_transform(df.iloc[:,:4], df.iloc[:, 4])
print('>>>检验统计值(相关系数):\n', sb.scores_)
print('\n>>>P值:\n', sb.pvalues_)
x_sb[:5]
>>>检验统计值(相关系数):
[ 0.78256123 -0.42665756 0.9490347 0.95654733]
>>>P值:
[2.89047835e-32 5.20156326e-08 4.20187315e-76 4.15531102e-81]
array([[1.4, 0.2],
[1.4, 0.2],
[1.3, 0.2],
[1.5, 0.2],
[1.4, 0.2]])
5.2.3.卡方检验
工作原理
卡方检验是检验定性自变量对定性因变量的相关性,求出卡方值,然后根据卡方值
匹配出其所对应的概率是否足以推翻原假设H0,如果能推翻H0,就启用备用假设H1。
理论公式及推导
假设检验:
假如提出原假设H0:化妆与性别没有关系;
备用假设H1:化妆与性别有显著关系。
卡方值(chi-square-value)计算公式
χ 2 = ∑ ( A − E ) 2 E = ∑ i = 1 k ( A i − n P i ) 2 n P i \chi^2=\sum\frac{(A-E)^2}{E}=\sum_{i=1}^k\frac{(A_i-nP_i)^2}{nP_i} χ2=∑E(A−E)2=i=1∑knPi(Ai−nPi)2
其中,Ai为i水平的观察(实际)频数,Ei为i水平的期望(理论)频数,n为总频数,pi为i水平的期望频率。
i水平的期望频数Ei等于总频数n×i水平的期望概率pi,k为单元格数(行数*列数)。
如何判定两个定性变量的卡方值在什么区间可以证明假设成不成立呢?
计算步骤如下:
- 计算 χ 2 卡 方 值 \chi_2卡方值 χ2卡方值
- 计算自由度(df=(行数-1)*(列数-1))
- 置信度(根据卡方值结合表格和自由度查询而得到的置信度大小)
优缺点
优点:可以很好地筛选出与定性应变量有显著相关的定性自变量。
应用场景及意义
应用场景:适用于分类问题的分类变量
# 调用 sklearn 模块 API 接口
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
skb = SelectKBest(chi2, k=2)
x_skb = skb.fit_transform(df.iloc[:,:4], df.iloc[:,4])
print('>>>检验统计值(卡方值):\n', skb.scores_)
print('\n>>>P值:\n', skb.pvalues_)
x_skb[:5]
>>>检验统计值(卡方值):
[ 10.81782088 3.7107283 116.31261309 67.0483602 ]
>>>P值:
[4.47651499e-03 1.56395980e-01 5.53397228e-26 2.75824965e-15]
array([[1.4, 0.2],
[1.4, 0.2],
[1.3, 0.2],
[1.5, 0.2],
[1.4, 0.2]])
5.2.4.互信息法
原理及实现参考资料-互信息原理及实现
工作原理
评价定性自变量对定性应变量的相关性
在处理分类问题提取特征的时候就可以用互信息来衡量某个特征和特定类别的相关性,
如果信息量越大,那么特征和这个类别的相关性越大。反之也是成立的。
理论公式及推导
-
互信息公式: M I ( X , Y ) = ∑ i = 1 X ∑ j = 1 Y P ( x i , y i ) log 2 P ( x i , y j ) P ( x i ) P ( y j ) MI(X,Y)=\sum_{i=1}^X\sum_{j=1}^YP(x_i,y_i)\log_2\frac{P(x_i,y_j)}{P(x_i)P(y_j)} MI(X,Y)=i=1∑Xj=1∑YP(xi,yi)log2P(xi)P(yj)P(xi,yj)
其中 P ( x i , y j ) = ∣ X i ∩ Y j ∣ N , P ( x i ) = X i N , P ( Y j ) = Y j N 其 中 N 是 总 样 本 数 P(x_i,y_j)=\frac{|X_i \cap Y_j|}{N},P(x_i)=\frac{X_i}{N},P(Y_j)=\frac{Y_j}{N}其中N是总样本数 P(xi,yj)=N∣Xi∩Yj∣,P(xi)=NXi,P(Yj)=NYj其中N是总样本数 -
标准互信息公式: N M I ( X , Y ) = 2 M I ( X , Y ) H ( X ) + H ( Y ) NMI(X,Y)=\frac{2MI(X,Y)}{H(X)+H(Y)} NMI(X,Y)=H(X)+H(Y)2MI(X,Y)
其中信息熵的公式 H ( X ) = − ∑ i = 1 X P ( x i ) l o g 2 ( P ( x i ) ) , 而 H ( Y ) = − ∑ j = 1 Y P ( y j ) l o g 2 ( P ( y j ) ) H(X)=-\sum_{i=1}^XP(x_i)log_2(P(x_i)),而H(Y)=-\sum_{j=1}^YP(y_j)log_2(P(y_j)) H(X)=−i=1∑XP(xi)log2(P(xi)),而H(Y)=−j=1∑YP(yj)log2(P(yj))
优缺点
应用场景及意义
应用场景:因此非常适合于文本分类的特征和类别的配准工作
# 互信息法
# 自己手写理论公式实现功能
# np.where(condition, x, y)
# 满足条件(condition),输出x,不满足输出y。
# numpy.intersect1d(ar1, ar2, assume_unique=False) [资源]
# 找到两个数组的交集。
# 返回两个输入数组中已排序的唯一值。
# math.log(x[, base])
# x -- 数值表达式。
# base -- 可选,底数,默认为 e
def MI_and_NMI():
import math
from sklearn import metrics
A = np.array([1,1,1,1,1,1,2,2,2,2,2,2,3,3,3,3,3])
B = np.array([1,2,1,1,1,1,1,2,2,2,2,3,1,1,3,3,3])
N, A_ids, B_ids = len(A), set(A), set(B)
# print(N, A_ids, B_ids)
# 互信息计算
MI, eps = 0, 1.4e-45
# 你说的这种应该是为了避免log0的结果
# 所以添加一个非常小的数字,避免无穷的...log(0)的情况
for i in A_ids:
for j in B_ids:
ida = np.where(A==i) # 返回索引
idb = np.where(B==j)
idab = np.intersect1d(ida, idb) # 返回相同的部分
#print(ida,idb,idab)
# 概率值
px = 1.0*len(ida[0])/N # 出现的次数/总样本数
py = 1.0*len(idb[0])/N
pxy = 1.0*len(idab)/N
# MI 值
MI += pxy * math.log(pxy/(px*py)+eps, 2)
# 标准互信息计算
Hx = 0
for i in A_ids:
ida = np.where(A==i)
px = 1.0*len(ida[0])/N
Hx -= px * math.log(px+eps, 2)
Hy = 0
for j in B_ids:
idb = np.where(B==j)
py = 1.0*len(idb[0])/N
Hy -= py * math.log(py+eps, 2)
NMI = 2.0*MI/(Hx+Hy)
return MI, NMI, metrics.normalized_mutual_info_score(A,B)
MI_and_NMI()
(0.565445018842856, 0.3645617718571898, 0.3646247961942429)
# # 调用 sklearn 模块 API 接口
# from sklearn.feature_selection import SelectKBest
# from minepy import MINE
# # 由于MINE的设计不是函数式的,定义mic方法将其为函数式的,
# # 返回一个二元组,二元组的第2项设置成固定的P值0.5
# def mic(x, y):
# m = MINE()
# m.compute_score(x, y)
# return (m.mic(), 0.5)
# fun = lambda X, Y: array(map(lambda x:mic(x, Y), X.T)).T
# # 选择K个最好的特征,返回特征选择后的数据
# skb_ = SelectKBest(fun, k=2)
# x_skb_ = skb_.fit_transform(df.iloc[:,:4], df.iloc[:,4])
# print('>>>检验统计值(卡方值):\n', x_skb_.scores_)
# print('\n>>>P值:\n', x_skb_.pvalues_)
# x_skb_[:5]
5.3.Wrapper 包装法
封装器用选取的特征子集对样本(标签)集进行训练学习,训练的精度(准确率)作为衡量特征子集好坏的标准,
经过比较选出最好的特征子集。
常用的有逐步回归(Stepwise regression)、向前选择(Forward selection)和向后选择(Backward selection)。
它的优点是:考虑了特征之间组合以及特征与标签之间的关联性;
缺点是:当观测数据较少时容易过拟合,而当特征数量较多时,计算时间又会增长。
工作原理
包装法是指使用算法模型对特征子集与目标(标签)集进行训练评估,根据训练的精度(准确率)衡量特征子集的好坏,从而挑选出最好的特征子集。
理论公式及推导
步骤:
-
组合好特征子集
假设特征X=[A,B,C],目标(标签)Y,那么特征子集可以有 2 特 征 数 2^{特征数} 2特征数组合方式:
X 1 = [ A ] , X 2 = [ B ] , X 3 = [ C ] , X 4 = [ A , B ] , X 5 = [ A , C ] , X 6 = [ B , C ] , X 7 = [ A , B , C ] , X 8 = [ ] X1=[A], X2=[B], X3=[C], X4=[A,B], X5=[A,C], X6=[B,C], X7=[A,B,C], X8=[] X1=[A],X2=[B],X3=[C],X4=[A,B],X5=[A,C],X6=[B,C],X7=[A,B,C],X8=[]
其中要剔除掉空集,进一步扩展特征子集的表达方式如下:
特 征 子 集 = X i , 其 中 i = [ 1 , 2 , . . . , ( 2 特 征 数 − 1 ) ] 特征子集=Xi,其中i=[1,2,...,(2^{特征数}-1)] 特征子集=Xi,其中i=[1,2,...,(2特征数−1)] -
将每个特征子集Xi分别与标签Y进行训练学习
model.fit(Xi,Y),其中i=[1,2,…,( 2 特 征 数 − 1 2^{特征数}-1 2特征数−1)] -
衡量特征好坏的不同方法
model.score(Xi,Y),可选择其他合理评估方法也可以
(1) 第一种(针对特征子集):从 2 特 征 数 − 1 2^{特征数}-1 2特征数−1个特征子集中挑选出训练精度(评分)对应最好的特征子集
(2) 第二种(针对单个特征):比如把含有A特征的所有特征子集的评分/频率(频数)作为相对应的衡量指标
根据评分指标,挑选出前k个MeanScore值较大的特征作为最终的特征
M e a n S c o r e ( A ) = ∑ i = 1 N s c o r e ( A ) N , N 表 示 含 有 特 征 A 的 所 有 特 征 子 集 的 次 数 , 比 如 本 例 子 含 有 A 的 特 征 子 集 有 4 次 MeanScore(A)=\frac{\sum_{i=1}^Nscore(A)}{N},N表示含有特征A的所有特征子集的次数,比如本例子含有A的特征子集有4次 MeanScore(A)=N∑i=1Nscore(A),N表示含有特征A的所有特征子集的次数,比如本例子含有A的特征子集有4次
根据频率指标,挑选出前k个F频率值较大的特征作为最终的特征 F ( A ) = 含 有 特 征 A 的 特 征 子 集 被 选 为 重 要 特 征 的 次 数 m 含 有 特 征 A 的 特 征 子 集 的 数 量 n F(A)=\frac{含有特征A的特征子集被选为重要特征的次数m}{含有特征A的特征子集的数量n} F(A)=含有特征A的特征子集的数量n含有特征A的特征子集被选为重要特征的次数m
**那么怎样才算被选为重要特征呢?**对应指标大于80%(可根据具体情况调整)的特征子集可以被认为是重要特征
优缺点
优点:考虑了特征之间组合以及特征与标签之间的关联性。
缺点:由于要划分特征为特征子集并且逐个训练评分,因此当特征数量较多时,计算时间又会增长;另外在样本数据较少的时候,容易过拟合。
应用场景及意义
5.3.1.稳定性选择(Stability Selection)
[1]https://www.cnblogs.com/stevenlk/p/6543646.html
工作原理
稳定性选择是一种基于**二次抽样和选择算法(训练模型)**相结合的方法,选择算法可以是回归、分类SVM或者类似算法。
原理实现:在不同的特征子集上运行训练模型,不断地重复,最终汇总特征选择的结果。比如可以统计某个特征被认为是重要特征的频率
(被选为重要特征的次数除以它所在的子集被测试的次数)。理想情况下,重要特征的得分会接近100%。稍微弱一点的特征得分会是非0的数,
而最无用的特征得分将会接近于0。
优缺点
优点:
- 特征值下降的不是特别急剧,这跟纯lasso的方法和随机森林的结果不一样,
能够看出稳定性选择对于克服过拟合和对数据理解来说都是有帮助的。 - 总的来说,好的特征不会因为有相似的特征、关联特征而得分为0。
- 在许多数据集和环境下,稳定性选择往往是性能最好的方法之一。
from sklearn.linear_model import RandomizedLasso, LinearRegression
from sklearn.linear_model import RandomizedLogisticRegression, LogisticRegression
import warnings
warnings.filterwarnings('ignore')
X = df.iloc[:,:4]
Y = df.iloc[:,4]
names = X.columns.tolist()
print(names)
# -------------------------------------
# 回归
rlasso = RandomizedLasso(alpha=0.025)
rlasso.fit(X, Y)
# -------------------------------------
# 分类
rlogistic = RandomizedLogisticRegression()
rlogistic.fit(X, Y)
print("\n>>>回归 Features sorted by their score:")
print(rlasso.scores_)
print(sorted(zip(map(lambda x: format(x, '.4f'), rlasso.scores_), names), reverse=True))
print("\n>>>分类 Features sorted by their score:")
print(rlogistic.scores_)
print(sorted(zip(map(lambda x: format(x, '.4f'), rlogistic.scores_), names), reverse=True))
lr = LinearRegression()
lr.fit(X,Y)
lr.coef_, lr.intercept_
['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
>>>回归 Features sorted by their score:
[0.13 0.075 0.56 0.585]
[('0.5850', 'petal_width'), ('0.5600', 'petal_length'), ('0.1300', 'sepal_length'), ('0.0750', 'sepal_width')]
>>>分类 Features sorted by their score:
[0.14 0.79 0.655 0.69 ]
[('0.7900', 'sepal_width'), ('0.6900', 'petal_width'), ('0.6550', 'petal_length'), ('0.1400', 'sepal_length')]
(array([-0.11190585, -0.04007949, 0.22864503, 0.60925205]),
0.18649524720624988)
from sklearn.svm import SVC
X1, X2, Y = df[['petal_width']], df[['sepal_width']], df['species']
svc = SVC()
for X in [X1, X2]:
svc.fit(X,Y)
print(svc.score(X,Y))
0.96
0.5533333333333333
小知提示:
从上面可以验证RandomizedLasso比RandomizedLogisticRegression更靠谱,
因此在日后使用过程中不要急着筛选,也要验证特征选择的合理性以及优越性。
5.3.2.递归特征消除
Recursive Feature Elimination,简称RFE
工作原理
主要思想是:
(1)反复的构建模型(比如SVM或者回归模型)
(2)接着选出最好(或者最差)的特征(可以根据系数来选),把选出来的特征放到一边
(3)然后在剩余的特征上重复上面(1)(2)步骤,直到遍历完所有特征。
通识来说:
RFE算法的主要思想就是使用一个基模型(这里是S模型VM)来进行多轮训练,
每轮训练后,根据每个特征的系数对特征打分,去掉得分最小的特征,
然后用剩余的特征构建新的特征集,进行下一轮训练,直到所有的特征都遍历了。
这个过程中特征被消除的次序就是特征的排序,实际上这是一种寻找最优特征子集的贪心算法。
优缺点
RFE的稳定性很大程度上取决于在迭代选择的时候,选择哪一种模型。
(1)如果RFE采用的是普通的回归,没有经过正则化的回归是不稳定的,从而RFE也是不稳定的
(2)如果采用Ridge或Lasso模型,经过正则化的回归是稳定的,从而RFE是稳定的。
from sklearn.feature_selection import RFE
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
boston = load_boston()
X = boston["data"]
Y = boston["target"]
names = boston["feature_names"]
#use linear regression as the model
lr = LinearRegression()
#rank all features, i.e continue the elimination until the last one
rfe = RFE(lr, n_features_to_select=2)
rfe.fit(X,Y)
print("Features sorted by their rank:")
print(sorted(zip(rfe.ranking_, names)))
Features sorted by their rank:
[(1, 'NOX'), (1, 'RM'), (2, 'CHAS'), (3, 'PTRATIO'), (4, 'DIS'), (5, 'LSTAT'), (6, 'RAD'), (7, 'CRIM'), (8, 'INDUS'), (9, 'ZN'), (10, 'TAX'), (11, 'B'), (12, 'AGE')]
5.3.3.特征值排序选择
概念及工作原理
理论上来讲,如果某个特征进行排序或者打乱之后,会很明显的影响(无论正向影响还是负向影响)到模型(预测评分)效果评分,
那么可以说明这个特征对模型来说是重要的;反之,说明这个特征存不存在并不会影响到模型的效能。
基于这么个原理,我们可以提出:
(1)特征在进行排序或者打乱之后,会很明显影响模型性能的特征,划定为重要特征。
(2)特征在进行排序或者打乱之后,对模型性能几乎没有影响,划定为不重要特征。
优缺点
应用场景及意义
5.4.Embedded 嵌入法
集成法,先使用某些机器学习的算法和模型进行训练,得到各个特征的权重值系数,
根据系数从大到小选择特征。类似于Filter方法,但是是通过训练来确定特征的优劣。
Regularization,或者使用决策树思想,Random Forest和Gradient boosting等
包装法与嵌入法的区别:包装法根据预测效果评分来选择,而嵌入法根据预测后的特征权重值系数来选择。
工作原理
先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。
有些机器学习方法本身就具有对特征进行打分的机制,或者很容易将其运用到特征选择任务中,
例如回归模型,SVM,树模型(决策树、随机森林)等等
5.4.1.线性模型
工作原理
越是重要的特征在模型中对应的系数就会越大,而跟目标(标签)变量越是无关的特征对应的系数就会越接近于0。
- 线性模型
在噪音不多的数据上,或者是数据量远远大于特征数的数据上,如果特征之间相对来说是比较独立的,
那么即便是运用最简单的线性回归模型也一样能取得非常好的效果
优缺点
缺点:
(1)如果特征之间存在多个互相关联的特征,模型就会变得很不稳定
(2)对噪声很敏感,数据中细微的变化就可能导致模型发生巨大的变化
from sklearn.linear_model import LinearRegression
X = df.iloc[:,:4]
Y = df.iloc[:,4]
lr = LinearRegression()
lr.fit(X,Y)
print(X.columns.tolist())
print(lr.coef_)
['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
[-0.11190585 -0.04007949 0.22864503 0.60925205]
5.4.2.正则化
概念:正则化就是把额外的约束或者惩罚项加到已有模型(损失函数)上,以防止过拟合并提高泛化能力。
损失函数由原来的 L ( X , Y ) L(X,Y) L(X,Y)变为 L ( X , Y ) + α ∣ w ∣ , , w L(X,Y)+\alpha \left| w \right| ,,w L(X,Y)+α∣w∣,,w是模型系数组成的向量(有些地方也叫参数parameter,coefficients), ∥⋅∥‖⋅‖一般是L1或者L2范数,α是一个可调的参数,控制着正则化的强度。
当用在线性模型上时,L1正则化和L2正则化也称为Lasso和Ridge。
工作原理
L1正则化Lasso(least absolute shrinkage and selection operator)将系数w的l1范数作为惩罚项加到损失函数上,由于正则项非零,这就迫使那些弱的特征所对应的系数变成0。因此L1正则化往往会使学到的模型很稀疏(系数w经常为0),这个特性使得L1正则化成为一种很好的特征选择方法。
L2正则化同样将系数向量的L2范数添加到了损失函数中。由于L2惩罚项中系数是二次方的,这使得L2和L1有着诸多差异,最明显的一点就是,L2正则化会让系数的取值变得平均。
优缺点
L1正则化缺点:L1正则化像非正则化线性模型一样也是不稳定的,如果特征集合中具有相关联的特征,当数据发生细微变化时也有可能导致很大的模型差异。
L2正则化优点:L2正则化对于特征选择来说一种稳定的模型,不像L1正则化那样,系数会因为细微的数据变化而波动。
总结:L2正则化和L1正则化提供的价值是不同的,L2正则化对于特征理解来说更加有用:表示能力强的特征对应的系数是非零。
from sklearn.linear_model import Lasso
X = df.iloc[:,:4]
Y = df.iloc[:,4]
lasso = Lasso(alpha=0.3)
lasso.fit(X,Y)
print(X.columns.tolist())
print(lasso.coef_)
['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
[ 0. -0. 0.3435091 0. ]
由上面情况来看,L1范数正则化效果非常差,几乎特征都被弱化了,不知道哪一些重要
from sklearn.linear_model import Ridge
X = df.iloc[:,:4]
Y = df.iloc[:,4]
ridge = Ridge(alpha=0.3)
ridge.fit(X,Y)
print(X.columns.tolist())
print(ridge.coef_)
['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
[-0.11327412 -0.03665944 0.23969479 0.58451798]
由上面情况来看,L2范数正则化从返回的回归系数就可以知道模型比较稳定,并且效果不错。
5.4.3.树模型
工作原理
随机森林具有准确率高、鲁棒性好、易于使用等优点,随机森林提供了两种特征选择的方法:
(1)平均不纯度减少
(2)平均精确率减少
6.类别标签不平衡处理
参考资料
概念和工作原理
(1)类别标签不平衡问题是指:
在分类任务中,数据集中来自不同类别的样本数目相差悬殊。
举个例子:
假设类别 A 的样本数量有 M 个,类别 B 的样本数量有 N 个,并且 M >>> N(假设 M:N=9:1),
这种情况我们就可以判定此数据集存在严重的类别标签不平衡的问题,为了防止模型出现严重误差,
因此在建模前需要就样本不平衡问题处理。
(2)类别不平衡问题会造成这样的后果:
在数据分布不平衡时,其往往会导致分类器的输出倾向于在数据集中占多数的类别。
输出多数类会带来更高的分类准确率,但在我们所关注的少数类中表现不佳。
(3)常用方法:
欠采样、过采样及加权处理。
(4)类别标签不平衡情况下的评价指标:
准确率在类别不平衡数据上,说服力最差。应考虑精确率、召回率、F1 值、F-R 曲线和 AUC 曲线。
6.1.欠采样
所谓欠采样是指把占比多的类别 A 样本数量(M=900)减少到与占比少的类别 B 样本数量(N=100)一致,然后进行训练。
(1)第一种方法(随机欠采样):
随机欠采样是指通过随机抽取的方式抽取类别 A 中 100 个样本数据与类别 B 中的 100 个样本进行模型训练。
理论公式推导 A n e w = M − ( M − N ) = d a t a s e t ( A r a n d o m ) ( N ) 个 A_{new}=M - (M-N)=dataset(A_{random})(N)个 Anew=M−(M−N)=dataset(Arandom)(N)个
随机欠采样的缺点:欠采样只是采取少部分数据,容易造成类别 A 的信息缺失
(2)第二种方法(代表性算法:EasyEnsemble 集成学习法):
算法思想:利用集成学习机制,将占比多的类别 A 样本数据划分为若干个样本子集供不同学习器使用,
这样对每个学习器来看都进行了欠采样,但在全局来看却不会丢失重要信息。
算法原理如下:
第一步:首先从占比多的类别 A 样本中独立随机抽取出若干个类别 A 样本子集。
第二步:将每个类别 A 的样本子集与占比少的类别 B 样本数据联合起来,训练生成多个基分类器。
第三步:最后将这些基分类器组合形成一个集成学习系统。集成可采用加权模型融合或者取所有基分类器总和的平均值。
EasyEnsemble 集成学习法优点:可以解决传统随机欠采样造成的数据信息丢失问题,且表现出较好的不均衡数据分类性能。
6.2.过采样
所谓过采样是指把占比少的类别 B 样本数量(N=100)扩增到占比多的类别 A 样本数量(M=900)一致,然后进行训练。
第一种方法(随机过采样):
由于随机过采样采取简单复制样本的策略来增加少数类样本,这样容易产生模型过拟合的问题,
即使得模型学习到的信息过于特别(Specific)而不够泛化(General),因此很少使用这种方法。
经典代表性算法是 SMOTE 算法:
SMOTE原理参考资料
SMOTE 的全称是 Synthetic Minority Over-Sampling Technique 即“人工少数类过采样法”,非直接对少数类进行重采样,
而是设计算法来人工合成一些新的少数样本。
算法原理如下:
(1)在占比少的类别 B 中随机抽取一个样本 a,从 a 的最近邻 k 个数据中又随机选择一个样本 b。
(2)在 a 和 b 的连线上(或者说[a,b]区间中)随机选择一点作为新的少数类样本。
6.3.加权处理
加权处理是指通过调整不同类型标签的权重值,增加占比少的类别 B 样本数据的权重,降低占比多的类别 A 样本数据权重,
从而使总样本占比少的类别 B 的分类识别能力与类别 A 的分类识别能力能够同等抗衡。
加权处理原理如下:
遍历每一个样本,设总样本占比多的类别 A 的权重为 W1(自定义),总样本占比少的类别 B 的权重为 W2(自定义),其中 W2 > W1。
其实这个也类似于对模型进行惩罚,从而影响各个类别标签的重要性。
7.降维
所谓的降维就是指采用某种映射方法,将原高维空间中的数据点映射到低维度的空间中。
7.1.无监督之主成分分析PCA
概念及工作原理
Principal Component Analysis(PCA)是最常用的线性降维方法,它的目标是通过某种线性投影,
将高维的数据映射到低维的空间中表示,并期望在所投影的维度上数据的方差最大,
以此使用较少的数据维度,同时保留住较多的原数据点的特性。
- 中心化
中心化的目的是防止不同特征之间不同的量纲影响,使每个特征都能被同等对待。常用中心化方法如下:
x m e a n = x − μ 或 者 x s t d = x − μ σ , 其 中 μ 是 均 值 、 σ 是 标 准 差 x_{mean}=x-\mu或者x_{std}=\frac{x-\mu}{\sigma},其中\mu是均值、\sigma是标准差 xmean=x−μ或者xstd=σx−μ,其中μ是均值、σ是标准差
中心化处理后的数据,均值为0 - 求协方差矩阵
协方差是衡量两个变量之间的相关关系
$$$$ - 求特征值和特征向量
- 将特征值从大到小排序,提取前k个特征值主成分所对应的特征向量
- 将原数据集映射相乘到新的特征向量中
def pca(df, k):
X = np.mat(df.iloc[:, :-1].as_matrix())
# 1 中心化
X_mean = X - np.mean(X, axis=0)
# 2 求协方差
cov = np.cov(X_mean.T)
# 3 求特征值和特征向量
w, v = np.linalg.eig(cov)
# 4 对特征值排序并提取前k个主成分所对应的特征向量
w_ = np.argsort(w)[::-1]
v_ = v[:, w_[:k]]
# 5 将原数据映射相乘到新的特征向量中
newF = X_mean * v_
return newF, w, v
newF, w, v = pca(df, k=3)
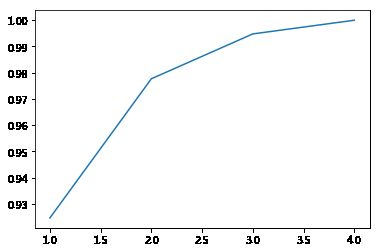
def best_k(w):
wSum = np.sum(w)
comsum_rate, goal_rate, count = 0, 0.98, 0
for k in range(len(w)):
CR = w[k]/wSum # 计算贡献率
print(CR)
comsum_rate += CR # 计算累加贡献率
count += 1
if comsum_rate >= goal_rate:
print('Best k .... 累加贡献率为:', comsum_rate, end='')
return count
best_k(w)
0.9246187232017269
0.05306648311706793
0.017102609807929763
Best k .... 累加贡献率为: 0.9947878161267246
3
# 贡献率累加曲线
def CRplot(w):
wSum = np.sum(w)
comsum_rate, L = 0, []
for k in range(len(w)):
CR = w[k]/wSum # 计算贡献率
comsum_rate += CR # 计算累加贡献率
L.append(comsum_rate)
plt.plot(range(1,5,1), L)
CRplot(w)
8.特征监控
- 特征有效性分析,比如特征重要性、权重
- 特征监控,比如监控重要特征,防止特征质量下降,影响模型效果
9.特征工程实行
特征工程流程没有强制固定先后顺序来处理, 但一般是在数据预处理、特征构造、特征选择以及特征降维之间循坏运用,
并没有固定一定要严格按照顺序来进行,可根据具体问题来具体使用。
参考文献:
[1] 特征工程参考系列1
[2] 特征工程参考系列2
[3]