手写数字识别实践（一）：基于朴素贝叶斯分类器与PyQt5

  选了个模式识别的课，好家伙老师上来就给任务写个手写数字识别的应用程序，还要有界面，语言不限，C、C++、Python、Java、Matlab都可以。Emmm……其实这个问题不算太大，毕竟就个人而言写程序这种实践类的事总是比学习概率论之类的理论分析稍微好受一些的QAQ……好了废话不多说，下面正式开始吧：
  编程及运行环境： VS Code + Win10（Ubuntu也是可以跑的）
  使用软件包： PIL + PyQt5 + numpy + pandas + matplotlib

一、理论基础

  无论对数学多头疼，不把理论上的东西整明白还是没法写程序的。
  首先明确一下需要用到的定义（不急，咱用专业的数学语言 人话 自己的理解 来慢慢展开），有基础可酌情跳至第二节：

1.条件概率

  条件概率 $P(A|B)$ ，就是指事件$B$发生的情况下，事件$A$发生的概率。公式可以直接在网上找到：$$P(A|B)=\frac{P(A\bigcap B)}{P(B)}$$

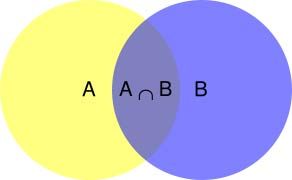
  从文氏图上的效果来看，$P(A|B)$ 就是将原本的考量范围缩小到了事件$B$必然发生的范围内（$P(A)$ 则是“原始”的考量范围下的推算结果）。
  相对地，有 $P(A|B)$ ，自然也就会有 $P(B|A)$ 。很明显 $$P(B|A)=\frac{P(A\bigcap B)}{P(A)}$$

2.全概率公式

  全概率公式，就是在条件概率的理论基础上，将原本的“原始”考量范围下的 $P(A)$ ，转化为各种条件下事件$A$发生概率的总和 ：$$P(A)=\sum _{i=1}^{n}P(A\bigcap B_i)=\sum _{i=1}^{n}P(A|B_i)P(B_i)$$  如下图所示，整个大圆为样本空间，中间阴影面积为事件$A$。大圆的每一个切分代表每一个$B_i$ 。

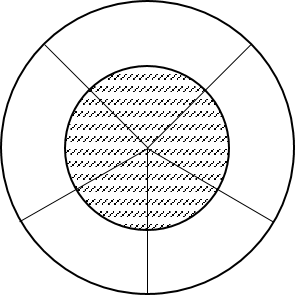
3.贝叶斯公式

  因为对于条件概率 $P(A|B)$ 和 $P(B|A)$ 来说，$P(A\bigcap B)$ 是一样的，所以将 $P(A|B)$ 和 $P(B|A)$ 的条件概率公式联立，就可以得到贝叶斯公式：$$P(A|B)=\frac{P(A\bigcap B)}{P(B)}=\frac{P(B|A)P(A)}{P(B)}$$  对上式做些小改动，得到：$$P(B_i|A)=\frac{P(A|B_i)P(B_i)}{P(A)}$$  如果再将 $P(A)$ 用全概率公式表示，即可得到贝叶斯公式的另一形态：$$P(B_i|A)=\frac{P(A|B_i)P(B_i)}{{\sum }_{j=1}^{n}P(A|B_j)P(B_j)}$$  其中，$P(B_i)$被称为先验概率， $P(B_i|A)$ 是事件$A$发生的条件下事件$B_i$发生的概率，也被称作后验概率。如果将事件$B_i$视作事件$A$发生的原因之一（$B_1$到$B_n$都是），那么上式所表达的含义就可以理解为：当事件$A$发生时，事件$B_i$是其原因的概率。这也是贝叶斯方法实现手写数字识别的基本公式，即当得到一张图片（事件A）时，求取图片上的数字是 X（0~9分别对应事件$B_1$ ~ $B_{10}$）的概率，最后算得谁的概率最大，就将这张图片判断为谁的手写数字。

4.朴素贝叶斯

  明确了贝叶斯公式应用于手写数字识别的理论基础，接下来要做的自然就是对纯理论的可行性进行优化，使之更加贴合实际，以便能顺利用于解决实际问题。朴素贝叶斯就是一种相对简单的优化方法，适合新手入门（所以博主选的也是朴素贝叶斯）。
  在正式介绍朴素贝叶斯方法之前再给没接触过相关领域的人扫个盲：关于手写数字识别是一种监督模式识别，需要用到的模型训练集/测试集，里面是包含图片和标签两个东西的，一张图片对应一个标签。所谓标签，就是用来明确告知 训练对象/测试对象 其对应图片的数字的。所以，在对模型进行训练的时候，实际上是要同时输入图片和标签的（测试的时候，标签则是用来检验识别结果，用于计算模型识别的准确率的）。那么，正式开始吧：
  首先确定求取概率对象。目标是计算出所有的 $P(B_i|A)$ ，然后找出最大值。那么，根据前面提到的公式可以知道，我们需要通过训练数据集计算出所有的先验概率 $P(B_i)$ 和条件概率 $P(A|B_i)$ 。
  如果用$X$表示图片集合，$Y$表示标签集合，则训练数据集就可以表示为$$T=\{(x_1,y_1),(x_2,y_2),...(x_n,y_n)\}$$  其中$x_1,x_2,...,x_n\in X$，$y_1,y_2,...y_n\in Y$，对每一个 $x_i\in X$，都有 $x_i=\{x_i^1,x_i^2,...,x_i^n\}$(意为第i个样本的第n个特征)。很明显对于训练数据集，$P(X,Y)$是独立同分布的，所以有 $P(X|Y)=\frac{P(X,Y)}{P(Y)}$ 。$$P(Y=c_k),k=0,1,...,9$$ $$P(X=x|Y=c_k)=P(X^1=x^1,X^2=x^2,...,X^n=x^n|Y=c_k)$$  上面两式即是要求的先验概率与条件概率。其中，先验概率 $P(Y)$ 好解决，可以自行给出理论上的概率（10%），也可以结合训练集的实际情况，通过统计各类数字的占比得出。但是条件概率 $P(X|Y)$ 却由于训练集的规模化而变得无法估计。
  如果假设 $P(X|Y)$ 的条件概率分布是特征条件独立的话，就可以将其表示为：$$P(X=x|Y=c_k)=\prod _{j=1}^{n}P(X^j=x^j|Y=c_k)$$

PS：如果看到这里有点懵的话，博主在这里简单地说明一下：对于任意输入的数字，取 $28\times 28$的图片，如果将所有的像素点都视作其特征，那么就会有 $28\times 28=784$个特征，而每一个特征都对应一个像素点的取值（像素值）。在朴素贝叶斯的假设条件下，这张图片是 “$1$”的概率 就是每一个特征 是 “$1$” 的特征的概率 的乘算。

  这样就以牺牲一定准确性的代价（实际上特征的出现并非是独立的而是有一定关联的），极大地简化了 $P(X|Y)$ 的求取过程，这就是朴素贝叶斯的“朴素”之处（不跟你玩什么花里胡哨的，怎么算简单就怎么来）。
  如此，后验概率 $P(Y|X)$ 的算式就可以写成：$$P(Y=c_k|X=x)=\frac{P(Y=c_k){\prod }_{j}P(X^j=x^j|Y=c_k)}{{\sum }_{k}P(Y=c_k){\prod }_{j}P(X^j=x^j|Y=c_k)}$$  再把公分母去掉，即可得到朴素贝叶斯分类器的最简形式：$$y=f(x)=\underset{c_k}{\mathrm{argmax}}P(Y=c_k)\prod _{j}P(X^j=x^j|Y=c_k)$$   就差最后一步了！最后利用极大似然估计来估计相应的 先验概率 $P(Y)$ 和条件概率 $P(X|Y)$ ：$$P(Y=c_k)=\frac{{\sum }_{i}I(y_i=c_k)}{N},k=0,1,...,9$$ $$P(X^j=a_{jl}|Y=c_k)=\frac{{\sum }_{i}I(x_i^j=a_{jl}|y_i=c_k)}{{\sum }_{i}I(y_i=c_k)},l=0,1$$   其中， $I$ 为指示函数，$l$ 在上式中代表二值化后的像素点取值情况，而 $j$ 则表示给定的图片 $x_i$ 对应的第 $j$ 个特征（像素点）。

PS：看懂了当然最好，不过看懵了也没关系，博主在这里继续将这些“意义不明”的公式翻译成人话。简单来说还是通过统计的方式，得出 $0、1、2、...、9$ 这10个数字对应到 $784$ 个特征，也就是像素点的概率分布。比如说对于第1个特征，有两种取值（后续直接将图片二值化，这样就只有0和1两种取值了），统计取0的次数中把图片归到0~9这十类的次数占比，就得到了对应的10个概率，同理统计取1的次数也能出来10个概率，第2个特征的每种取值也对应10个概率…统计完成，极大似然估计到此为止，之后对于任意输入的图片($28\times 28$)，784个特征值都是已知的，接下来就根据后验概率的简化算式，按着之前统计出来的概率分布进行乘算，最后取最大概率对应的数字作为识别到的数字。

二、程序设计实践

1.流程图

  首先是程序的运行流程设计。因为数据集的预处理被单独拉出来安排了，所以这里的流程图实际上是完成了数据预处理部分以后的，因此第一步就是直接从文件里读取数据了。读完数据以后就是训练和测试，完了以后就可以自己写数字检验识别效果啦（关键环节后面都会提及）。

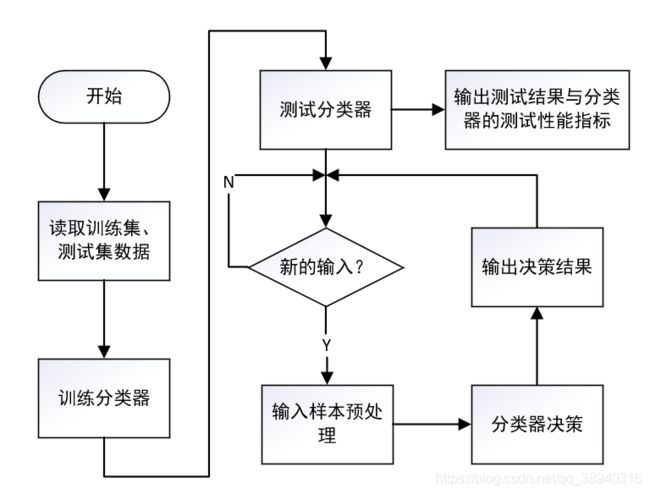
2. 数据预处理

  首先从网站上下载MNIST数据集

  可以看出在 train-images.idx3-ubyte 中，第一个数为 32 位的整数（魔数，图片类型的数），第二个数为32位的整数（图片的个数），第三和第四个也是 32 位的整数（分别代表图片的行数和列数），接下来的都是一个字节的无符号数（即像素，值域为0~255），因此，我们只需要依次获取魔数和图片的个数，然后获取图片的长和宽，最后逐个按照图片大小的像素读取就可以得到一张张的图片内容了。标签数据集及测试数据集的的数据读取都是一样的原理。这里分享一下 piao 来的python处理脚本：

from PIL import Image
import struct
import numpy as np
import os
from PIL import Image

def read_image(filename):
    f = open(filename, 'rb')
    index = 0
    buf = f.read()
    f.close()
    # 开始读取 魔数、图片数目、图片行数、列数
    magic, images, rows, columns = struct.unpack_from('>IIII', buf, index)
    index += struct.calcsize('>IIII')
    for i in range(images):
        # 逐个读取图片，每个图片字节数为 行数X列数
        image = Image.new('L', (columns, rows))
        for x in range(rows):
            for y in range(columns):
                # 读取并填充图片的像素值，每个像素值为一个字节
                image.putpixel((y, x), int(struct.unpack_from('>B', buf, index)[0]))
                index += struct.calcsize('>B')
        print('save ' + str(i) + 'image')
        image.save('这里设置图片存储路径' + str(i) + '.png')

def read_label(filename, saveFilename):
    f = open(filename, 'rb')
    index = 0
    buf = f.read()
    f.close()
    # 开始读取 魔数及标签数目
    magic, labels = struct.unpack_from('>II', buf, index)
    index += struct.calcsize('>II')
    labelArr = [0] * labels
    for x in range(labels):
        # 一个标签一个字节
        labelArr[x] = int(struct.unpack_from('>B', buf, index)[0])
        index += struct.calcsize('>B')
    save = open(saveFilename, 'w')
    save.write(','.join([str(x) for x in labelArr]))
    save.write('\n')
    save.close()
    print('save labels success')
    return labelArr

N = 28
def get_train_set():
    f = open('这里设置data.csv文件的路径', 'wb')
    category = read_label('这里设置train-labels.idx1-ubyte文件的路径（gz包解压出来就是）', '这里设置label.txt文件的路径，和图片要在同一目录下')

    file_names = os.listdir(r"图片与label.txt的所在目录", )
    train_picture = np.zeros([len(file_names)-1, N ** 2 + 1])
    # 遍历文件，转为向量存储
    for file in range(len(file_names)-1):
        train_im = Image.open('图片存储路径 + %d.png' % (file))
        img_num = np.array(train_im)
        rows, cols = img_num.shape
        for i in range(rows):
            for j in range(cols):
                if img_num[i, j] < 100:
                    img_num[i, j] = 0
                else:
                    img_num[i, j] = 1
        train_picture[file, 0:N ** 2] = img_num.reshape(N ** 2)
        train_picture[file, N ** 2] = category[file]
        print("完成处理第%d张图片" % (file+1))
    np.savetxt(f,train_picture,fmt='%d',delimiter=',', newline='\n', header='', footer='')
    f.close()
    return train_picture

def get_test_set():
    f = open('test.csv')			#和上面一样设置路径
    category = read_label('t10k-labels.idx1-ubyte', 'label.txt')	#设置路径

    file_names = os.listdir(r"", )	#设置路径
    test_picture = np.zeros([len(file_names)-1, N ** 2 + 1])
    # 遍历文件，转为向量存储
    for file in range(len(file_names)-1):
        train_im = Image.open('%d.png' % (file))	#设置路径
        img_num = np.array(train_im)
        rows, cols = img_num.shape
        for i in range(rows):
            for j in range(cols):
                if img_num[i, j] < 100:
                    img_num[i, j] = 0
                else:
                    img_num[i, j] = 1
        test_picture[file, 0:N ** 2] = img_num.reshape(N ** 2)
        test_picture[file, N ** 2] = category[file]
        print("完成处理第%d张图片" % (file+1))
    np.savetxt(f,test_picture,fmt='%d',delimiter=',', newline='\n', header='', footer='')
    f.close()
    return test_picture

if __name__ == '__main__':
    #训练集图像和标签解压
    read_image('train-images.idx3-ubyte')
    read_label('train-labels.idx1-ubyte', 'label.txt')
    #遍历文件，转为向量存储（图像矩阵+标签整合）
    get_train_set()

	#这俩由于保存图片操作没有拉出接口需要分开运行，不能一起跑。当然也可以自己修改程序，增加形参
	#我是懒得改了
    #测试集图像和标签解压
    #read_image('t10k-images.idx3-ubyte')
    #read_label('t10k-labels.idx1-ubyte', 'label.txt')
    #遍历文件，转为向量存储（图像矩阵+标签整合）
    #get_test_set()

  程序跑完，就可以得到60000张图片和1个标签txt文本（电脑性能偏弱的谨慎打开，不然可能会卡成翔，虽然总共才十几兆但是架不住它文件数量多）以及一个$60000\times 785$的Excel表格（将每张图片二值化以后转化为了行向量，最后给每张图片都打上标签，这个csv文件同样请谨慎打开）：

  Excel表格中，最后一列非零值就是各行向量的标签了。

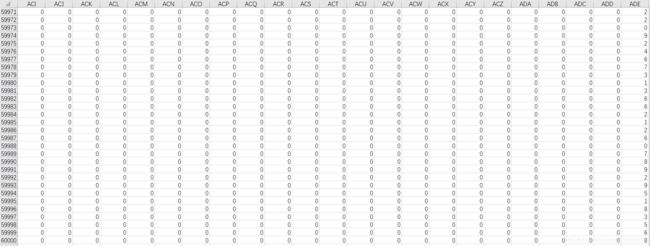
  测试集的处理也是类似的。

3. 模型训练（训练集数据统计）

def Train(trainset, train_labels):
    global prior_probability,conditional_probability
    prior_probability = np.zeros(class_num)                         #先验概率
    conditional_probability = np.zeros((class_num,feature_len,2))   #条件概率

    #计算先验概率及条件概率
    for i in range(len(train_labels)):
        img = trainset[i]                                           #图像二值化，但由于之前已经做好了图像数据预处理，这里直接抓取对应的行向量
        label = train_labels[i]

        prior_probability[label] += 1

        for j in range(feature_len):
            conditional_probability[label][j][img[j]] += 1

    for i in range(class_num):
        for j in range(feature_len):
            #经过二值化后像素点只有 0 和 1 两种取值
            pix_0 = conditional_probability[i][j][0]
            pix_1 = conditional_probability[i][j][1]

            #计算对应像素点取0、1的条件概率
            probability_0 = (float(pix_0) / float(pix_0 + pix_1)) * 1000000 + 1     #float型保留到小数点后六位，这里放大一百万倍尽量使小数位计算数据不丢失,再加1防止出现概率为0的情况
            probability_1 = (float(pix_1) / float(pix_0 + pix_1)) * 1000000 + 1

            conditional_probability[i][j][0] = probability_0
            conditional_probability[i][j][1] = probability_1
    return prior_probability, conditional_probability

4. 模型预测

#计算概率
def caculate_probability(img, label):
    probability = int(prior_probability[label])

    for i in range(len(img)):
        probability *= int(conditional_probability[label][i][img[i]])

    return probability

def Test_Predict(testset, test_labels):
    pre_right = np.zeros(10)                    # 每一类预测正确的数量
    act_numbers = np.zeros(10)                  # 每一类的样本实际数量（P）
    predict = []                                # 预测结果
    accuracy = []                               # 预测准确率

    # 统计测试数据中各类数字的数量
    for i in test_labels:
        act_numbers[i] += 1

    for i in range(len(testset)):
        max_label = 0
        max_probability = caculate_probability(testset[i], 0)

        for j in range(1, 10):
            probability = caculate_probability(testset[i], j)

            if max_probability < probability:
                max_label = j
                max_probability = probability
        predict.append(max_label)

        if max_label == test_labels[i]:
            pre_right[test_labels[i]] += 1
        if (i+1) % 500 == 0:
            accuracy.append(float(pre_right.sum())/(i+1))
            
	print(pre_right)
    print('-------------------------------------------------------------------')
    print(act_numbers)
    print('-------------------------------------------------------------------')
    print(pre_right/act_numbers)

    plt.figure()
    plt.plot(np.arange(1,21),accuracy,marker="o",markersize=8)
    plt.xlabel("x -- 1:500")
    plt.title("Predict Accuracy Rate")
    plt.show()

    return accuracy, np.array(predict)

三、实际效果

  以下是博主利用PyQt5设计的程序界面：

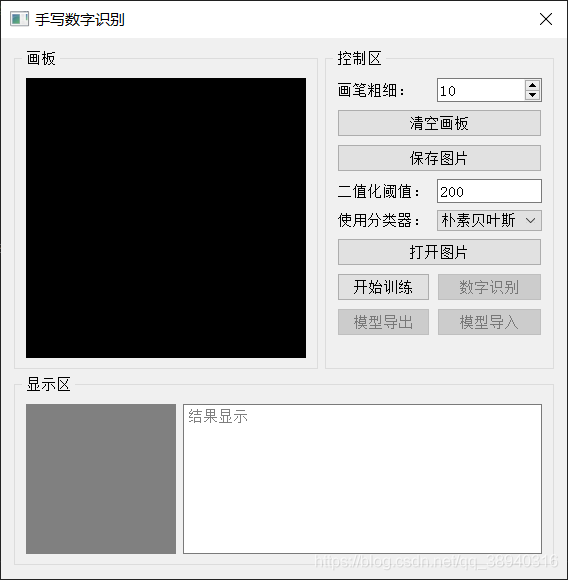
  以下是测试结果（博主没有加入计时模块，暂时没有这方面的需求，如有需要可自行添加）：

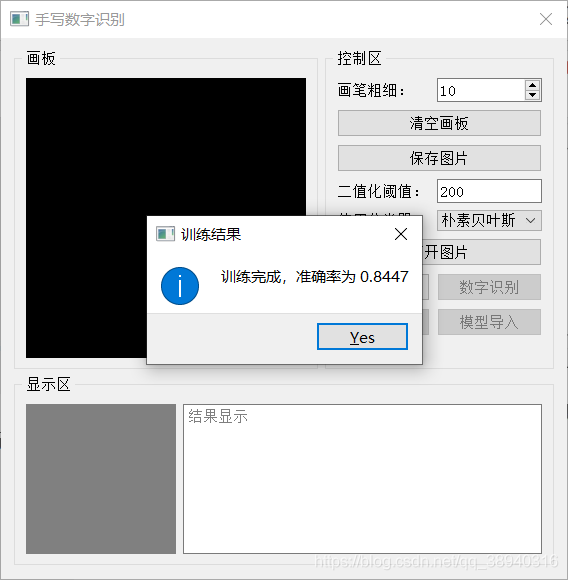
  事实上博主一直都觉得这种总体准确率指标最多给一个大概的直观感受，实际上还不如分别统计各类的准确率指标有价值……

  这三个数组分别对应每一类预测正确数、每一类实际样本数、每一类的识别准确率。这里对分类器性能的展示更加直观一些：

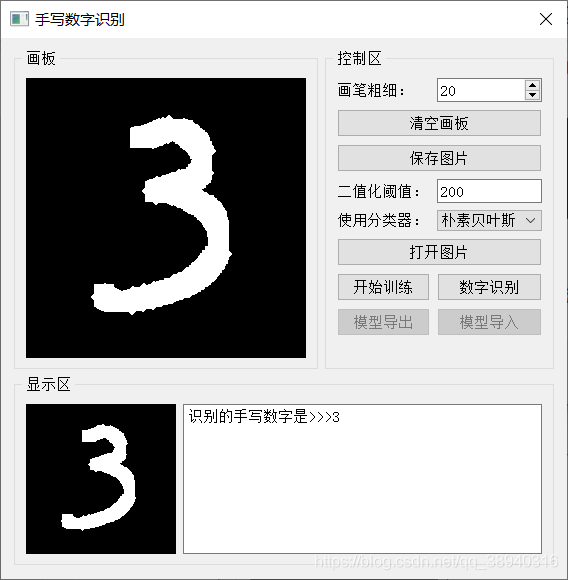
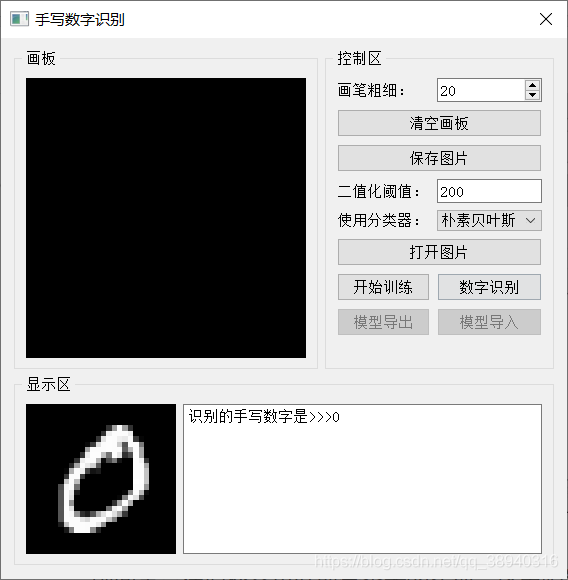
四、一些补充（咕~）

1. 图片读取:博主设计的识别程序有两种输入方式：一是通过画板输入，二是通过“打开图片”的按钮在本地文件夹指定图片读取（识别示例中那个看起来比较糊的 “$0$” 就是按钮方式读取的训练集图片）。MNIST提供的训练集和测试集中的图片都是$28\times 28$的，而实际上UI里展示的画板与显示区是绝对不可能设成这么小的，因此需要进行图像缩放。画板的大小为$280\times 280$，显示区则为$150\times 150$（这个真就只是用来显示的），因此在画板上画完以后先缩放到$150\times 150$传递给显示区，然后二次缩放到$28\times 28$传递给分类器进行预测，也正是因为这样会压缩像素点，可能导致关键特征丢失，因此增设了调节画笔粗细的接口（实际上自己测都是用最粗的画笔）。按钮打开方式则是直接读取到$28\times 28$传递给分类器，然后放大到$150\times 150$传递给显示区。
   画板模块的添加可以参考这位兄台： PyQt5实例 画板小程序
2. 输入样本预处理：MNIST数据集中的图片已经被脚本安排得妥妥的（完成了二值化，转成了行向量，还打上了标签），但是画板端输入图片并没有被安排，而且打开图片按钮的作用对象并不局限于MNIST数据集中的图片，所以需要自行将传递过来的图像二值化，转换成行向量以后再传递给分类器进行预测。下图就是画板端输入的图片二值化后的实际效果（能隐约看出来是上文的第一个测试结果 “3”）：
   
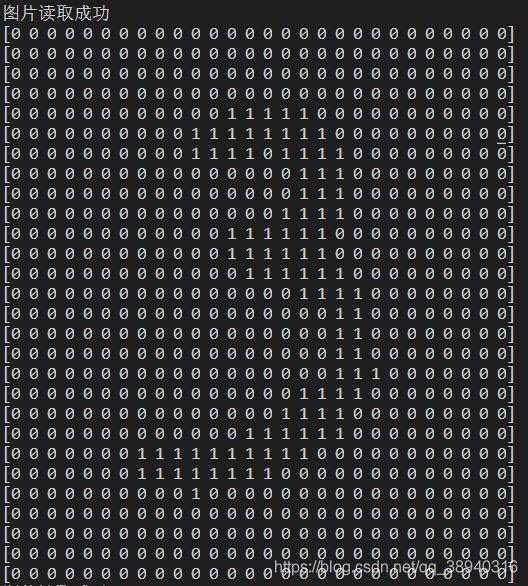
   这是图片的预处理函数。形参 threshold 对应UI上的二值化阈值，以便随时调整二值化效果。

def pretreatment(ima, threshold):
    ima = ima.convert('L')            #转化为灰度图像
    im = np.array(ima)                #转化为二维数组
    for i in range(im.shape[0]):      #转化为二值矩阵
        for j in range(im.shape[1]):
            if im[i, j] > threshold:
                im[i, j] = 1
            else:
                im[i, j] = 0
    return im

3. 关于PyQt5：上一次用 Qt 还是在两年前，自己用 Qt 做了个虚拟示波器，Qt 里相当一部分组件都在那次的学习中有所了解与应用，故不在此赘述，仅记录有新突破的知识点（要用啥组件百度一下就一大把教程）。好吧其实也就是UI的布局问题，之前用 Qt 的时候是直接用 Qt Designer 怼的UI，一直都不太理解布局这块的东西，所以用的全是绝对布局。这次尝试脱离 Qt Designer 直接用 Python 撸出来，布局这块算是学到拿过来就可以用的程度了。
   布局管理参考这位兄台，写得非常清楚：Pyqt5系列(九)-基本布局管理
4. 局限性：本文中采用的实现方式是直接取784个像素点作为特征，简单粗暴，虽然通过训练后算得测试准确率为84.77%，其实不然。毕竟在自己手写输入的时候，读入的图片上取的是数字和画板的绝对位置，而非相对位置（即在图像上确定好数字边界再进行特征划分）。要想准确地识别出手写的数字而非数据集中的图片，就得照着数据集里的图片来写数字（经博主测试，自己写的数字识别准确率实在一言难尽）。拟定的优化思路是拿到二值化的图像以后利用边缘提取的思想把数字外围部分“切出来”，然后重新划分区域作为新的特征，这样既可以降维简化计算又可以解决掉绝对位置的问题。至于博主，在公开模式识别课程相关的博客时大抵已经脱离苦海了，当然能理直气壮地鸽掉这个优化。
5. ROC曲线：一开始除了计算每一类的识别准确率外其实还想画一下ROC曲线，然而在调分类阈值的时候发现概率被放大太多倍（极限值差不多到了 $10^{4708}$ 这样子 Orz）实在难以调整，那就这样吧，朴素贝叶斯这就鸽了，之后的分类器里有机会再加上ROC。
6. 最小风险贝叶斯决策：本文实现的朴素贝叶斯分类器使用的是基于最小错误率的贝叶斯决策方法（毕竟决策准则是看谁的概率最大）。实际上还有一种衍生类决策，也就是最小风险的贝叶斯决策，简单来说就是在得到后验概率以后不是通过取最大值来做出决策，而是引入损失函数，转而取最小值作为决策结果（其实就是人为地做一个加权）。单类的判别函数用公式表示就是下面这样：$$R_i(X)=\sum _{j=1}^K\lambda ({\alpha }_i,j)P(Y=c_k|X)$$   ${\alpha }_i$ 为将 $X$ 判为 $c_i$ 类的决策，$\lambda ({\alpha }_i,j)$ 表示 $X$ 实属于 $c_j$ ,由于采用 ${\alpha }_i$ 决策而被判为 $c_i$ 时造成的损失。
7. 杂：暂时先这样吧。看老师的意思，贝叶斯识别手写数字还只是个开始，后面还要加其他的模型，所以博主在设计UI的时候预留了分类器选择项。模型的导入和导出功能还没有实装。关于模型的训练（统计）等待，原本博主是准备加装一个进度条模块，这样训练的时候就不用干等着总给人一种死机了的感觉，不过后来一找资料发现实装进度条会破坏代码的连贯性（因为要把计算部分单独抓出来再开一个线程），所以也鸽了。

五、参考资料

• 李航《统计学习方法》第4章 朴素贝叶斯法
• 朴素贝叶斯应用之在手写数字识别的实践
• 李航《统计学习方法》第四章——用Python实现朴素贝叶斯分类器（MNIST数据集）
• 条件概率、贝叶斯公式和全概率公式
• 详解最大似然估计（MLE）、最大后验概率估计（MAP），以及贝叶斯公式的理解
• NLP面试-最大似然估计与贝叶斯估计的区别
• CSDN数学公式指导手册

六、复习阶段追加——正态分布概率模型下的最小错误率贝叶斯决策（理论）

  前面提及贝叶斯公式：$$P(B_i|A)=\frac{P(A|B_i)P(B_i)}{{\sum }_{j=1}^{n}P(A|B_j)P(B_j)}$$   对于上式，实现手写数字识别的思路就是：忽略公有分母简化计算、求先验概率 $P(B_i)$ 和 条件概率 $P(A|B_i)$ 。而正态分布和朴素贝叶斯的区别就在于它们对条件概率的求法不同。朴素贝叶斯是假设特征条件独立，然后直接拿特征的统计概率进行乘算，从本质上来说，训练就是制表，预测就是查表；正态分布则是假设 $P(A|B_i)$ 的概率密度函数服从多元正态分布，这样就得到了真正意义上的判别函数（参数待定），然后根据训练集数据估计出各个参数后装载到判别函数中，完成分类器的设计。
  先简化一下判别函数（$x$为 n 维的输入样本，$w_i$为 $x$ 的类别）：$$g_i(x)=P(x|w_i)P(w_i)$$   假设$P(x|w_i)$~$N({\mu }_i,{\Sigma }_i),i=1,...,c$ ，则$$g_i(x)=\frac{P(w_i)}{(2\pi {)}^{\frac{n}{2}}|{\Sigma }_i{|}^{\frac{1}{2}}}exp\{-\frac{1}{2}(x-{\mu }_i{)}^T{\Sigma }_i^{-1}(x-{\mu }_i)\}$$   取对数得到 $$g_i(x)=-\frac{1}{2}(x-{\mu }_i{)}^T{\Sigma }_i^{-1}(x-{\mu }_i)-\frac{n}{2}ln2\pi -\frac{1}{2}ln|{\Sigma }_i|+lnP(w_i)$$   上式中，${\mu }_i=E[X_i]$ 为第 $i$ 类样本集 $X_i$ 的 n 维均值向量 ；${\Sigma }_i=E[(X_i-{\mu }_i)(X_i-{\mu }_i{)}^T]$ 为第 $i$ 类样本集 $X_i$ 的 n x n 维协方差矩阵；${\Sigma }_i^{-1}$ 是 ${\Sigma }_i$ 的逆矩阵；$|{\Sigma }_i|$ 是 ${\Sigma }_i$ 的行列式。
  对 ${\Sigma }_i$ 的情况进行分类讨论：
  1.${\Sigma }_i={\sigma }^{2}I$，即各类的协方差矩阵都相等（ $I$ 为单位矩阵），类内各特征间相互独立，且方差 ${\sigma }^2$ 相等，则 ${\Sigma }_i^{-1}=\frac{1}{{\sigma }^2}I,|\Sigma |={\sigma }^{2n}$
  代入$g_i(x)$，忽略掉与类别 $i$ 无关的项，得$$g_i(x)=-\frac{(x-{\mu }_i{)}^T(x-{\mu }_i)}{2{\sigma }^2}+lnP(w_i)$$   如果各类先验概率 $P(w_i)$ 是相等的，那么上式的后一项就可以忽略，决策函数就能简化为 $$g_i(x)=-\frac{||x-{\mu }_i|{|}^2}{2{\sigma }^2}$$   由于上式的分子对应的几何意义为 $x$ 到第 $i$ 类的均值向量 ${\mu }_i$ 的欧氏距离的平方，所以此时的决策规则变为 $$\underset{i}{\mathrm{argmin}}||x-{\mu }_i|{|}^2$$   如果各类先验概率 $P(w_i)$ 不全相等，则可将 $(x-{\mu }_i{)}^T(x-{\mu }_i)$ 展开后去除与类别 $i$ 无关的项 $x^{T}x$，得到 $$g_i(x)=-\frac{1}{2{\sigma }^2}(-2{\mu }_i^{T}x+{\mu }_i^T{\mu }_i)+lnP(w_i)=(\frac{1}{{\sigma }^2}{\mu }_i{)}^{T}x+[-\frac{1}{2{\sigma }^2}{\mu }_i^T{\mu }_i+lnP(w_i)]$$   此时的决策规则为 $$\underset{i}{\mathrm{argmax}}{g}_i(x)$$

PS:对于欧氏距离取 $argmin$ 的情况，考虑到前面有一个 “$-$” 号，其实和 $argmax$ 的情况也没差，嫌麻烦统一记为 $argmax$ 也是可以的。对于下面的情况同样适用。

  2.${\Sigma }_i=\Sigma$，即各类的协方差矩阵都相等，${\Sigma }_1={\Sigma }_2=...={\Sigma }_n=\Sigma$，此时 $\Sigma$ 与 $i$ 无关，则 $$g_i(x)=-\frac{1}{2}(x-{\mu }_i{)}^T{\Sigma }^{-1}(x-{\mu }_i)+lnP(w_i)$$   如果各类先验概率 $P(w_i)$ 相等，同理可将决策函数简化为 $$g_i(x)=-\frac{1}{2}(x-{\mu }_i{)}^T{\Sigma }^{-1}(x-{\mu }_i)=-\frac{{\gamma }^2}{2}$$   和之前的欧氏距离类似，这里的 ${\gamma }^2$ 是马氏距离的平方，决策规则同样可以转化为取最小值。
  如果各类先验概率 $P(w_i)$ 不全相等，则将$(x-{\mu }_i{)}^T{\Sigma }^{-1}(x-{\mu }_i)$ 展开后去除与类别 $i$ 无关的项 $x^T{\Sigma }^{-1}x$，得到线性形式的判别函数 $$g_i(x)=({\Sigma }^{-1}{\mu }_i{)}^{T}x+[-\frac{1}{2}{\mu }_i^T{\Sigma }^{-1}{\mu }_i+lnP(w_i)]$$   3.一般情况，即各类的协方差矩阵不相等，此时情况相对复杂一些，因为只有第二项与 $i$ 无关可以忽略。$g_i(x)$ 此时为 $x$ 的二次型，这里不做讨论（不会真有老师要考查这种情况吧，不会吧不会吧）。
  拿到简化的判别函数以后，再用最大似然估计方法确定相关参数：
  直接上公式：$$\widehat{{\mu }_i}=\frac{1}{N}\sum _{j=1}^N{x}_j$$ $$\widehat{{\Sigma }_i}=\frac{1}{N}\sum _{j=1}^N(x_j-\widehat{{\mu }_i})(x_j-\widehat{{\mu }_i}{)}^T$$   上式中，$N$ 为第 $i$ 类的样本总数，$x_j$ 为第 $i$ 类的第 $j$ 个样本。
  小结一下，正态分布概率模型下贝叶斯手写数字分类器的实现步骤：

1. 利用训练集样本求均值向量 ${\mu }_i=[{\mu }_1,{\mu }_2,...,{\mu }_n{]}^T=E[X]$
2. 利用训练集样本求协方差矩阵 ${\Sigma }_i=E[(X-{\mu }_i)(X-{\mu }_i{)}^T]$
3. 根据 ${\Sigma }_i$ 对角线上的方差情况确定判别函数 $g_i(X)$ 的简化形式
4. 确定需要计算的 ${\Sigma }_i^{-1}$ 和 $|{\Sigma }_i|$
5. 求各类先验概率
6. 将求得的参数代入到选定的判别函数中，得到分类器（每一类都有1个判别函数，一共10个）
7. 根据贝叶斯公式计算出后验概率，取最大值对应的类别作为手写数字的类别