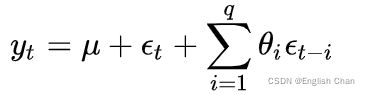ARIMA（p,d,q）模型原理及其实现 --------python

 1.简介

ARIMA模型(Autoregressive Integrated Moving Average model)，差分整合移动平均自回归模型，又称整合移动平均自回归模型，时间序列预测分析方法之一。ARIMA(p,d,q)中，AR是"自回归"，p为自回归项数;MA为"滑动平均"，q为滑动平均项数，d为使之成为平稳序列所做的差分次数(阶数)。"差分"一词虽未出现在ARIMA的英文名称中，却是关键步骤。

2.模型原理

在描述ARIMA模型，那么就离不开AR、MA、ARMA模型，下面先阐述这两个模型。

2.1 AR模型(自回归)

自回归只适用于预测与自身前期相关的现象，数学模型表达式如下：

其中是当前值，是常数项，是阶数，是自相关系数，​​​​​是误差，同时

要符合正态分布。 

该模型反映了在t时刻的目标值值与前t-1~p个目标值之前存在着一个线性关系，即：

 2.2 MA模型（移动平均）

 移动平均模型关注的是自回归模型中的误差项的累加，数学模型表达式如下：

该模型反映了在t时刻的目标值值与前t-1~p个误差值之前存在着一个线性关系，即：

2.3 ARMA模型（自回归移动平均）

该模型描述的是自回归与移动平均的结合，具体数学模型如下：

2.4 ARIMA模型

基本原理：将数据通过差分转化为平稳数据，再将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。

AR是自回归，p为自回归项；MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数，一般做一阶差分，很少做二阶差分。

2.5 ACF

​​​ACF 是一个完整的自相关函数，可为我们提供具有滞后值的任何序列的自相关值。简单来说，它描述了该序列的当前值与其过去的值之间的相关程度。时间序列可以包含趋势，季节性，周期性和残差等成分。ACF在寻找相关性时会考虑所有这些成分

2.6 PACF

偏自相关函数PACF 只描述观测值和其滞后项之间的直接关系，调整了其他较短滞后项的影响。

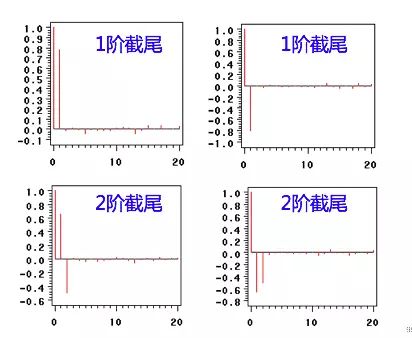
2.7 拖尾与截尾

截尾：在大于某个常数k后快速趋于0为k阶截尾

拖尾：始终有非零取值，不会在k大于某个常数后就恒等于零(或在0附近随机波动)

 例子：

3.定阶（p,d,q)

3.1 定d

因为AR（自回归）建立必须具有平稳性，所以在建立ARIMA模型也需要平稳性，使数据平稳性的方法可以讲数据进行差分处理，如一阶差分即t与t-1的差值，二阶差分为一阶差分基础上再进行一次差分，使数据平稳后的差分次数即为我们要定的参数d。

3.2 方法① 定p，q

• 若PACFp阶段后截尾，则截尾的阶数即为模型所确定的参数p。
• 若ACFq阶段后截尾，则截尾的阶数即为模型所确定的参数q。

3.3 方法② 定p，q

采用AIC或BIC原则，模型中AIC或BIC值越小，模型就越好。

4.假设检验

下面介绍在用python实现ARIMA模型使用到的假设检验。

4.1单位根检验（ADF）

在建立ARIMA模型的前，要讲将数据平稳化，即需要对数据进行差分处理，一般进行一节差分即可，一般一节差分就可以通过检验，如果一阶不通过，就再进行一次差分，即二阶差分，但不是差分的次数越多越好，它可能会导致数据信息的损失。检验数据平不平稳，第一种方法可以通过直接观察差分后的折线图。第二种方法就是通过假设检验，即单位根检验：

注：这里没有详细描述检验原理，只是简单介绍其原假设与备择假设，感兴趣可查找相关资料。

4.2残差正态性检验

完成模型建立，需要对模型的残差进行正态性检验，python中scipy库中的stats类提供了一个 normaltest函数，用于检验数据是否符合正太性：

残差是否符合正态性不一定要用假设检验，也可以观察残差的qq图，当qq图的散点位于一条直线时候说明是符合正态分布，同时也可以绘制残差频数直方图，下面会介绍检验、qq图、频数直方图实现代码。

 4.3残差序列独立性检验

一个较好的ARIMA模型，残差序列之间是独立性的，检验德宾-沃森（Durbin-Watson）检验简称D-W检验，是目前检验自相关性最常用的方法，但它只适用于检验一阶自相关性。 先通过公式计算出DW值，再根据样本容量n和解释变量数目k查分布表，得到临界值dl和du，然后判断是否自相关，当DW值等于2左右时，模型不存在一阶自相关。

注：这里没有详细描述检验原理，只是简单介绍检验判别方法，感兴趣可查找相关资料。

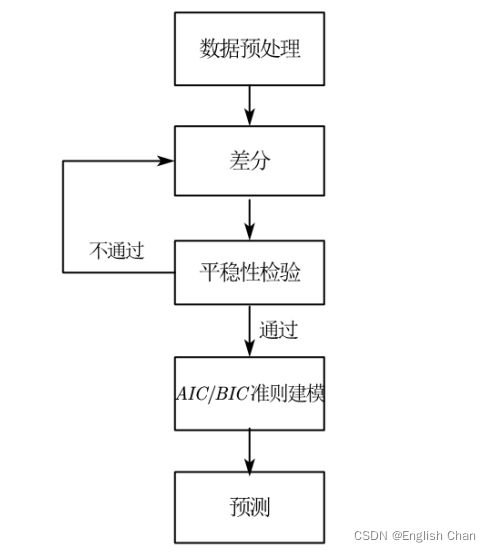
5.建模基本流程

6.python实现ARIMA

这次建模所用到的库如下代码，若还没有安装，在cmd窗口输入 pip install 库名   即可安装。

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import matplotlib
import seaborn as sns
from  statsmodels.tsa.arima_model  import  ARIMA
import statsmodels as sm
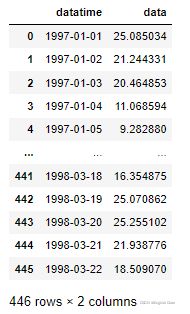
from scipy import stats 

6.1数据展示

这是笔者的数据，只要构造好这个dataframe数据类型就可以继续下面的步骤，该数据用变量data接受，下面的代码针对data变量都是针对这个数据集。

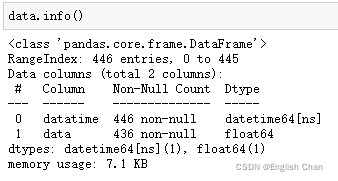
6.2缺失值处理

data.info()

发现数据集存在缺失值，对于时间序列数据缺失值不能简单的使用全体数据均值、中位数、众数处理，最常用的方法有前后加权均值法、线性插值法、n最近邻均值法填充，本次采用n=2的n最近邻均值法填充，比如n取2，则用t-2,t-1，t+1,t+2时刻的平均值来填充缺失的t时刻的值，代码实现如下：

#找出有缺失值的行  data[["data"]].isnull().T.any().values
def knm(df,n):
    #找出缺失值的行
    temp = df.isnull().T.any().values
    temp_df = df.copy()
    for i in range(len(temp)):
        if temp[i] == True:
            if i < n-1:                  #前n个
                 temp_df.loc[i,"data"] = df.loc[i:i+n,"data"].mean()  
            elif i > len(temp) - 1 -n:     #后n个
                 temp_df.loc[i,"data"] = df.loc[i-n:i,"data"]
            else:
                 print(df.loc[i-n:i+n,"data"])
                 temp_df.loc[i,"data"] = df.loc[i-n:i+n,"data"].mean()  
                 print(i-n,i+n+1)
    return temp_df
not_miss = knm(data[["data"]],2)
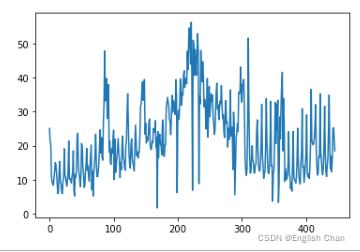
data["data"] = not_miss.values

 6.3数据可视化展示

plt.plot(data.iloc[:,1])
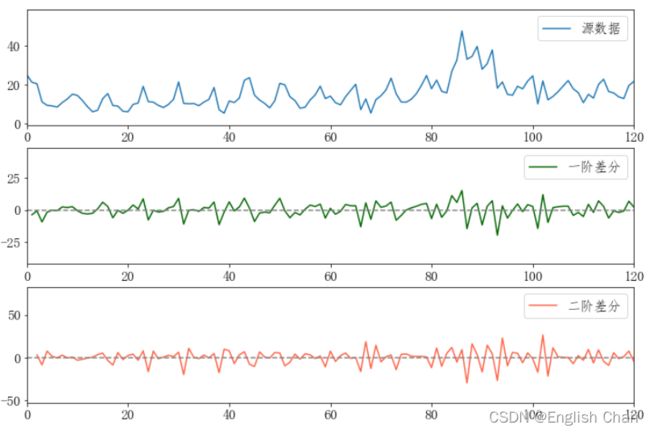
plt.hist(data.iloc[:,1],bins=20)

6.4数据平稳化

data["diff_1"] = data["data"].diff(1)  #一阶差分
data["diff_2"] = data["data"].diff(1)  #二阶差分

#分别画出ACF(自相关)和PACF（偏自相关）图像
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf

def diff(df,col):
    font = {"size":15,
       "family":"fangsong"}
    matplotlib.rc("font",**font)
    matplotlib.rcParams['axes.unicode_minus']=False
    
    df["diff_1"] = df[col].diff(1)  #一阶差分
    df["diff_2"] = df["diff_1"].diff(1)  #二阶差分
    
    #平稳数据折线图
    plt.figure(figsize=(12,8))
    plt.subplot(3,1,1)
    plt.plot(df[col].values,label="源数据")
    plt.xlim(0,120)
    plt.legend()
    plt.subplot(3,1,2)
    plt.plot(df["diff_1"].values,c="darkgreen",label="一阶差分")
    plt.plot([0,120],[0,0],"--",c = "grey")
    plt.xlim(0,120)
    plt.legend()
    plt.subplot(3,1,3)
    plt.plot(df["diff_2"].values,c="tomato",label="二阶差分")
    plt.plot([0,120],[0,0],"--",c = "grey")
    plt.xlim(0,120)
    plt.legend()
    plt.show()
    
    #ACF PACF
    print("-"*50,"未平稳数据ACF与PACF","-"*50)
    fig = plt.figure(figsize=(12,8))
    ax1 = fig.add_subplot(211)
    fig = plot_acf(df[col], lags=40,ax = ax1)
    ax2 = fig.add_subplot(212)
    plot_pacf(df[col], lags=40,ax = ax2)
    plt.show()
    
    #一阶差分后的ACF PACF
    print("-"*50,"一阶差分数据ACF与PACF","-"*50)
    fig = plt.figure(figsize=(12,8))
    ax1 = fig.add_subplot(211)
    fig = plot_acf(df["diff_1"][1:].values, lags=40,ax = ax1)
    ax2 = fig.add_subplot(212)
    plot_pacf(df["diff_1"][1:], lags=40,ax = ax2)
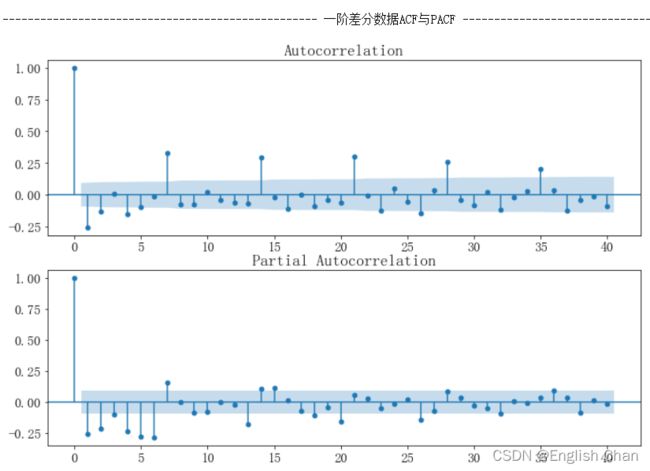
    plt.show()
    
diff(data,"data")

一阶自相关与偏相关图都呈现出拖尾现象，无法从这两图确定p与q。

6.5数据平稳性检验 单位根检验 

#未差分平稳性检测（ADF检验、单位根检验）
from  statsmodels.tsa.stattools  import  adfuller  as  ADF
print(u'原始序列的ADF检验结果为：',  ADF(data["data"]))
#返回值依次为adf、pvalue、usedlag、nobs、critical  values、icbest、regresults、resstore  p<0.05时表示稳定

#一阶差分平稳性检测（ADF检验、单位根检验）
from  statsmodels.tsa.stattools  import  adfuller  as  ADF
print(u'一阶差分序列的ADF检验结果为：',  ADF(data["diff_1"][1:]))
#返回值依次为adf、pvalue、usedlag、nobs、critical  values、icbest、regresults、resstore  p<0.05时表示稳定

一阶差分单位根检验p值<0.05，原始序列p值>0.05，于是ARIMA中的参数d定为1。

6.6根据bic/aic指标定p、q

#定阶
# pmax  =  int(len(df["失业率"])/10)  #一般阶数不超过length/10
# qmax  =  int(len(df["失业率"])/10)  #一般阶数不超过length/10
pmax = 5
qmax = 5
bic_matrix  =  []  #bic矩阵
for  p  in  range(pmax+1):
    tmp  =  []
    for  q  in  range(qmax+1):  #存在部分报错，所以用try来跳过报错。
        try:
            tmp.append(ARIMA(data["data"],order=(p,1,q)).fit().bic) 
        except:
            tmp.append(None)
    bic_matrix.append(tmp)
bic_matrix  =  pd.DataFrame(bic_matrix)  #从中可以找出最小值
p,q  =  bic_matrix.stack().idxmin()  
# #先用stack展平，然后用idxmin找出最小值位置。
print(u'BIC最小的p值和q值为：%s、%s'  %(p,q))

#定阶
# pmax  =  int(len(df["失业率"])/10)  #一般阶数不超过length/10
# qmax  =  int(len(df["失业率"])/10)  #一般阶数不超过length/10
pmax = 5
qmax = 5
aic_matrix  =  []  #bic矩阵
for  p  in  range(pmax+1):
    tmp  =  []
    for  q  in  range(qmax+1):  #存在部分报错，所以用try来跳过报错。
        try:
            tmp.append(ARIMA(data["data"],order=(p,1,q)).fit().aic) 
        except:
            tmp.append(None)
    aic_matrix.append(tmp)
aic_matrix  =  pd.DataFrame(bic_matrix)  #从中可以找出最小值
p,q  =  bic_matrix.stack().idxmin()  
# #先用stack展平，然后用idxmin找出最小值位置。
print(u'AIC最小的p值和q值为：%s、%s'  %(p,q))

根据aic/bic最小原则都筛选出p=5，q=3。

6.7模型拟合 AIRMA(5,1,3)

arima513 = ARIMA(data["data"],order=(5,1,3)).fit()
arima513.summary2()

 

6.7模型检验

resid=arima513.resid  #残差
plt.figure(figsize=(12,8))
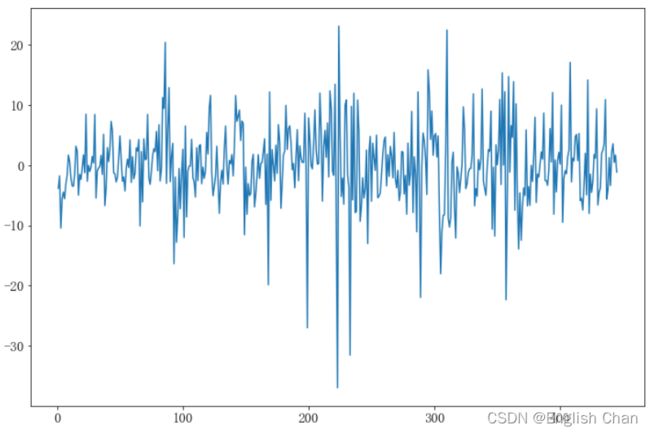
plt.plot(resid)

6.7.1残差正态性检验

stats.normaltest(resid)#检验序列残差是否为正态分布    pvalue=0.00028625258929196876   <  0.05  拒绝原假设 认为残差符合正太分布

 

p<0.05,接受备择假设，认为残差具有正态性

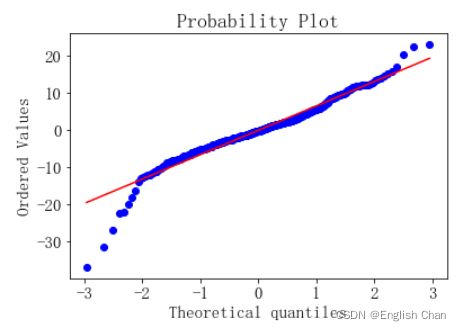
stats.probplot(resid, dist="norm", plot=plt)
plt.show()
plt.hist(resid,bins=50)
plt.show()

 

qq图散点基本在直线上，同时直方图也呈现正态性。

6.7.2残差序列自相关 （残差序列是否独立）

from statsmodels.stats.stattools import durbin_watson
durbin_watson(arima513.resid.values)     ##DW检验：靠近2——正常；靠近0——正自相关；靠近4——负自相关

 DW值非常靠近2，说明序列不具有相关性。

7.绘制原数据和预测数据对比图

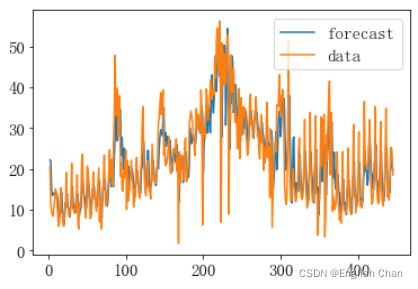
# 绘制原数据和预测数据对比图
arima513.plot_predict(dynamic=False)
plt.show()

通过观察预测值与实际值折线图，可以直观看出该模型拟合程度不怎么好，待优化

 

​​