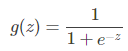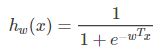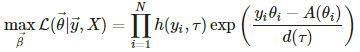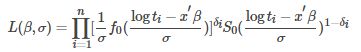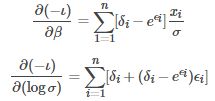Spark Machine Learning(SparkML):机器学习(部分二)
目录
6.分类和回归
6.1分类(Classification)
逻辑回归(LR)
决策树分类器(DTC)
随机森林分类器(RFC)
梯度提升树分类器(GBTC)
多层感知器分类器(MLPC)
线性支持向量机(SVM)
One-vs-Rest分类器
朴素贝叶斯(NB)
6.2回归(Regression)
线性回归(LR)
广义线性回归(GLR)
决策树回归(DTR)
随机森林回归(RFR)
梯度提升树回归(GBDT)
生存回归(Survival regression)
等渗回归(Isotonic regression)
6.3线性方法-正则化
6.4决策树
输入列(Input Columns)
输出列(Output Columns)
6.5树集合(Tree Ensembles)
随机森林(Random forest)
梯度提升树(GBTs)
7.聚类(Clustering)
7.1聚类分析基本步骤:
1.数据预处理
2.确定维度
3.确定聚类个数
4.选择合适的聚类方法
5.聚类结果分析与展示
7.2聚类算法的种类:
7.3 K均值聚类(K-means)
7.4文档主题模型(LDA)
7.5 二分K-均值算法(Bisecting k-Means)
7.6高斯混合模型(GMM)
7.7层次聚类(Hierarchical / Agglomerative)
6.分类和回归
分类与回归都是有监督学习,本质是一样的,都是特征(feature)到结果/标签(label)之间的映射,只不过分类的结果是离散值,回归是连续的。
区分分类任务和回归任务有一个简单方法,就是问一个问题:输出是否具有某种连续性。如果在可能的结果之间具有连续性,那么它就是一个回归问题。
6.1分类(Classification)
分类问题的目标是预测类别标签(class label),这些标签来自预定义的可选列表。分类问题有时可分为二分类(binary classification,在两个类别之间进行区分的一种特殊情况)和多分类(multiclass classification,在两个以上的类别之间进行区分)。你可以将二分类看作是尝试回答一道是/否问题。将电子邮件分为垃圾邮件和非垃圾邮件就是二分类问题的实例。在这个二分类任务中,要问的是/否问题为:“这封电子邮件是垃圾邮件吗?”。在二分类问题中,我们通常将其中一个类别称为正类(positive class),另一个类别称为反类(negative class)。这里的“正”并不代表好的方面或正数,而是代表研究对象。因此在寻找垃圾邮件时,“正”可能指的是垃圾邮件这一类别。将两个类别中的哪一个作为“正类”,往往是主观判断,与具体的领域有关。
分类: 预测一个给定样本的结果,其输出变量的形式为类别。样本含有标签,比如男性和女性、生病的和健康的等等。分类方法是一种对离散型随机变量建模或预测的监督学习算法(必须事先明确知道各个类别的信息,并且断言所有待分类项都有一个类别与之对应)。
分类算法包括逻辑回归,决策树、随机森林、贝叶斯、人工神经网络、K-近邻、支持向量机和基于关联规则等等,适合解决有监督形式的机器学习。
现实生活中常常用来预测(一个类别或类别的概率),使用案例包括邮件过滤(是否是垃圾邮件)、金融欺诈、用户是否会流失、明天是否会下雨和预测雇员异动等输出为类别的任务。同时部分模型也支持多种分类的预测,如保险业保单风险评级(A,B,C,D,E等级)。
对于分类问题,评价指标是准确率,它定义为测试样本集中被正确分类的样本数与测试样本总数的比值。精度和召回率也是分类问题的评价指标。
名词解释补充说明:
考虑一个二分问题,即将实例分成正类(positive)或负类(negative)。对一个二分问题来说,会出现四种情况。如果一个实例是正类并且也被 预测成正类,即为真正类(True positive),如果实例是负类被预测成正类,称之为假正类(False positive)。相应地,如果实例是负类被预测成负类,称之为真负类(True negative),正类被预测成负类则为假负类(false negative)。
True Positive(真正, TP): 被模型预测为正的正样本;
True Negative(真负, TN): 被模型预测为负的负样本 ;
False Positive(假正, FP): 被模型预测为正的负样本;
False Negative(假负, FN): 被模型预测为负的正样本;
True Positive Rate(真正率, TPR)或灵敏度(sensitivity): TPR = TP /(TP + FN) 正样本预测结果数 / 正样本实际数
True Negative Rate(真负率, TNR)或特指度(specificity): TNR = TN /(TN + FP) 负样本预测结果数 / 负样本实际数
False Positive Rate(假正率, FPR) :FPR = FP /(FP + TN) 被预测为正的负样本结果数 /负样本实际数
False Negative Rate(假负率, FNR) :FNR = FN /(TP + FN) 被预测为负的正样本结果数 / 正样本实际数
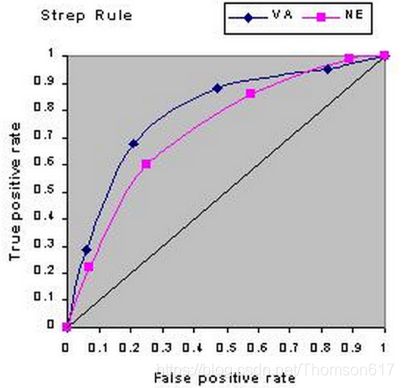
ROC (Receiver Operating Characteristic,接收机操作曲线): 把假正率当x轴,真正率当y轴画一个二维平面直角坐标系。然后不断调优检测方法(或机器学习中的分类器)的阈值,即最终得分高于某个值就是阳性,反之就是阴性,得到不同的真正率和假正率数值,然后描点。就可以得到一条ROC曲线。 需要注意的是,ROC曲线必定起于(0,0),止于(1,1)。因为当全都判断为阴性(-)时就是(0,0);全部判断为阳性(+)时就是(1,1)。这两点间斜率为1的线段表示随机分类器(对真实的正负样本没有区分能力)。所以一般分类器需要在这条线上方。
AUC(Area Under Curve):这条ROC曲线下方的面积。越接近1表示分类器越好。
精确度/查准率(Precision):P = TP/(TP+FP) ; 反映了被分类器判定的正例中真正的正例样本的比重。
准确率(Accuracy):A = (TP + TN)/(P+N) = (TP + TN)/(TP + FN + FP + TN); 反映了分类器统对整个样本的判定能力——能将正的判定为正,负的判定为负。
召回率/查全率(Recall),也称为 True Positive Rate: R = TP/(TP+FN) = 1 - FN/T; 反映了被正确判定的正例占总的正例的比重。
F-measure(又称F-score):F-Measure是Precision和Recall加权调和平均。F = 2 * 召回率 * 准确率/ (召回率+准确率);这就是传统上通常说的F1 measure。
逻辑回归(LR)
逻辑回归(Logistic Regression)即对数概率回归,是预测分类响应的常用方法,属于判别模型。这是广义线性模型的一个特例,可以预测结果的概率。
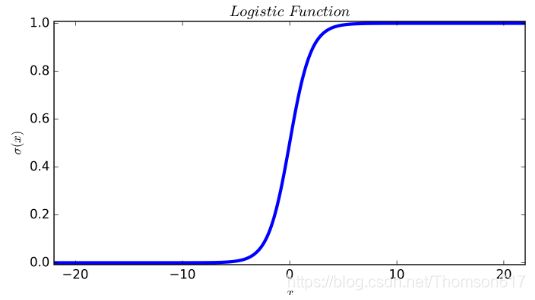
逻辑回归通过Logistic函数(即Sigmoid函数)将预测映射到0到1中间,因此预测值就可以看成某个类别的概率。它对某些数据与事物的归属(分到哪个类别)及可能性(分到某一类别的概率)进行评估。
逻辑回归的使用场景:
(1).寻找危险因素:寻找某一疾病的危险因素等(疾病诊断);
(2).预测:根据模型,预测在不同的自变量情况下,发生某病或某种情况的概率有多大.例如广告点击预估CTR(Click Through Rate,点击率);
(3).判别:实际上跟预测有些类似,也是根据模型判断某人属于某病或属于某种情况的概率有多大,也就是看一下这个人有多大的可能性是属于某病。
优点:输出有很好的概率解释,并且算法也能正则化而避免过拟合。Logistic 模型很容易使用随机梯度下降和新数据更新模型权重。
缺点:Logistic 回归在多条或非线性决策边界时性能比较差。
逻辑回归的本质是线性回归,只是在特征到结果的过程上加上了一层映射(逻辑回归将线性回归的输出范围压缩到了0~1之间)。即首先需要把特征进行求和,然后将求和后的结果应用于一个g(z)函数。g(z)可以将值映射到0或者是1上面。
MLlib逻辑回归的方程:
逻辑回归的损失函数是:
逻辑回归使用L2正则化方法:
每一个样本的梯度的计算方法为:倾斜度gradient = (1 / (1 + exp(- w * x) ) - y)* x
margin = - w * x
multiplier = 1 / (1 + exp(margin) ) - y
gradient = multiplier * x
每个样本的误差:
权重的更新方法:
weight = weight -alpha*(gradient + regParam * weight)
逻辑回归主要包含以下代码:
1) 伴生对象类:LogisticRegressionWithSGD.(包含有静态train方法)
2) 逻辑回归的主类:LogisticRegressionWithSGD,这个类继承了GeneralizedLinearAlgorithm类。同时执行了父类的run方法。不过里面的部分参数,比如说梯度下降方法,权重更新方法在LogisticRegressionWithSGD有新的定义。父类包含有optimizer.optimize方法。用于执行梯度下降。权重的优化计算调用的是runMiniBatchWithSGD。梯度的计算调用的是Gradient.compute 方法。
3) 逻辑回归模型:LogisticRegressionModel类。其里面也包含有predict方法来进行预测。
在逻辑回归中,可以使用二项逻辑回归来预测二元结果,或者可以使用多项逻辑回归来预测多类结果。使用该family 参数在这两种算法之间进行选择,或者不设置,Spark将推断出正确的变量。通过将family参数设置为“multinomial”,可以将多项逻辑回归用于二进制分类。它将产生两组系数和两个截距。
当在不具有常量非零列的数据集上截断LogisticRegressionModel时,Spark MLlib为常量非零列输出零系数。此行为与R glmnet相同,但与LIBSVM不同。
处理流程:
更多详情参见:https://blog.csdn.net/stevekangpei/article/details/75331960
二项逻辑回归(二分类)
二项Logistic回归(Binomial logistic regression)是工业界应用非常广泛的一个经典的二分类模型。一般就叫逻辑回归。首先使用logistic函数 σ(⋅) 将 z 从实数
空间 (−∞,+∞) 映射到概率空间 (0,1) 上,可以将映射之后的值 σ(z) 解释为样本
x 属于正类(记类别标记为1)的可能性,也就是后验概率的估计值:
既然解释成后验概率,然后就可以给出分类规则(最大后验概率决策):当 P(y=1|x)>0.5 ,认为样本 x 属于正类;否则样本 x 属于正类属于负类。
更多背景和有关二项logistic回归的实现请参阅logistic-regression.
例子:下面的例子展示了如何训练具有正则化的二项和多项逻辑回归模型来进行二分类。elasticNetParam对应于α、regParam对应λ。
Scala代码:
import org.apache.spark.ml.classification.LogisticRegression
import org.apache.spark.sql.{DataFrame, SparkSession, functions}
val training = spark.read.format("libsvm").load("/sample_libsvm_data.txt").toDF(“indexedLabel”,”indexedFeatures”)
//LR建模
val lr = new LogisticRegression()
.setLabelCol("indexedLabel") //设置标签列
.setFeaturesCol("indexedFeatures") //设置特征列
.setMaxIter(10) //设置最大迭代次数.默认是100。具体迭代次数可能在不足最大迭代次数停止
.setTol(1e-6) //设置容错(默认1e-6),每次迭代会计算一个误差,误差值随着迭代次数增加而减小,当误差小于设置容错,则停止迭代.
.setRegParam(0.3) //设置回归参数(正则化项系数),默认值是0。正则化主要用于防止过拟合现象,如果数据集较小,特征维数又多,易出现过拟合,考虑增大正则化系数
.setElasticNetParam(0.8) //正则化范式比,默认是0。正则化有两种方式:L1(Lasso)和L2(Ridge),L1用于特征的稀疏化,L2用于防止过拟合
.setPredictionCol("click_predict") //设置预测列
val lrModel = lr.fit(training)
// 为逻辑回归打印系数和截距
println(s"系数: ${lrModel.coefficients} 截距: ${lrModel.intercept}")
val pred = lrModel.transform(training)
pred.select("click_index","click_predict","probability").show(10,false)
// 也可以用多项式族进行二元分类
val mlr = new LogisticRegression()
.setMaxIter(10)
.setRegParam(0.3)
.setElasticNetParam(0.8)
.setFamily("multinomial") //对标签分布的描述,默认为“auto”.如果numClasses == 1 或 numClasses == 2,设置为“binomial”二项式。否则,设置为“multinomial”多项式.
val mlrModel = mlr.fit(training)
// 打印多项式族逻辑回归的系数和截距
println(s"Multinomial coefficients: ${mlrModel.coefficientMatrix}")
println(s"Multinomial intercepts: ${mlrModel.interceptVector}")
/**
spark.ml逻辑回归的实现还支持在训练集上提取模型摘要。注意:在LogisticRegressionSummary中存储为DataFrame的预测和度量被标注为@transient,因此只能在驱动程序中使用。LogisticRegressionTrainingSummary 提供了摘要 LogisticRegressionModel。在二进制分类的情况下,可以使用某些附加度量,例如ROC曲线。可以通过该binarySummary方法访问二进制摘要 。
*/
val trainingSummary = lrModel.binarySummary
// 获得每次迭代的目标.
val objectiveHistory = trainingSummary.objectiveHistory
println("objectiveHistory:")
objectiveHistory.foreach(loss => println(loss))
// 获取接收方操作特性作为dataframe 和areaUnderROC.
val roc = trainingSummary.roc
roc.show()
println(s"areaUnderROC: ${trainingSummary.areaUnderROC}")
// 设置模型阈值,使F-Measure最大化
val fMeasure = trainingSummary.fMeasureByThreshold
val maxFMeasure = fMeasure.select(functions.max("F-Measure")).head().getDouble(0)
import spark.implicits._
val bestThreshold = fMeasure.where($"F-Measure" === maxFMeasure).select("threshold").head().getDouble(0)
lrModel.setThreshold(bestThreshold)Python代码:
from pyspark.ml.classification import LogisticRegression
# 加载训练数据
training = spark.read.format("libsvm").load("/sample_libsvm_data.txt")
lr = LogisticRegression(maxIter=10, regParam=0.3, elasticNetParam=0.8)
# Fit the model
lrModel = lr.fit(training)
# 为逻辑回归打印系数和截距
print("Coefficients: " + str(lrModel.coefficients))
print("Intercept: " + str(lrModel.intercept))
# 我们也可以用多项式族进行二元分类
mlr = LogisticRegression(maxIter=10, regParam=0.3,
elasticNetParam=0.8, family="multinomial")
mlrModel = mlr.fit(training)
# 打印多项式族逻辑回归的系数和截距
print("Multinomial coefficients: " + str(mlrModel.coefficientMatrix))
print("Multinomial intercepts: " + str(mlrModel.interceptVector))
trainingSummary = lrModel.summary
# 获得每次迭代的目标
objectiveHistory = trainingSummary.objectiveHistory
print("objectiveHistory:")
for objective in objectiveHistory:print(objective)
# 获取接收方操作特性作为dataframe 和areaUnderROC.
trainingSummary.roc.show()
print("areaUnderROC: " + str(trainingSummary.areaUnderROC))
# 设置模型阈值,使F-Measure最大化
fMeasure = trainingSummary.fMeasureByThreshold
maxFMeasure = fMeasure.groupBy().max('F-Measure').select('max(F-Measure)').head()
bestThreshold = fMeasure.where(fMeasure['F-Measure'] == maxFMeasure['max(F-Measure)'])
.select('threshold')
.head()['threshold']
lr.setThreshold(bestThreshold)多项逻辑回归(多分类)
在多项式逻辑回归中,该算法产生K组系数,即K×J维矩阵,其中K为结果类数,J为特征数。如果算法符合截距项,则可以得到截距的长度K向量。
多项式系数可用作系数矩阵coefficientMatrix,截距可用作截距向量interceptVector。
用最小二乘训练的logistic回归模型的系数和截距方法。
coefficients和intercept不支持使用多项式族训练的逻辑回归模型的方法。使用coefficientMatrix和interceptVector替代。
利用softmax函数对结果类k∈1,2,…,k的条件概率进行建模:
我们利用多项式响应模型,利用弹性混合惩罚来控制过拟合,使加权负对数似然最小化。
有关详细的推导,请参阅Multinomial_logistic_regression:
下面的例子展示了如何用正则化范式比训练一个多类逻辑回归模型,并提取多类训练摘要来评估模型。
Scala代码:
import org.apache.spark.ml.classification.LogisticRegression
// Load training data
val training = spark.read.format("libsvm").load("/sample_multiclass_classification_data.txt")
// setFamily有三个选项:"auto","binomial","multinomial".默认值为"auto".
val lr = new LogisticRegression()
.setMaxIter(10)
.setRegParam(0.3)
.setElasticNetParam(0.8)
.setFamily("multinomial") //设置为多项逻辑回归
val lrModel = lr.fit(training)
// 打印多项逻辑回归的系数和截距
println(s"Coefficients: ${lrModel.coefficientMatrix}")
println(s"Intercepts: ${lrModel.interceptVector}")
val trainingSummary = lrModel.summary
// 获得每次迭代的目标
val objectiveHistory = trainingSummary.objectiveHistory
println("objectiveHistory:")
objectiveHistory.foreach(println)
// 对于multiclass,我们可以根据每个标签检查指标
println("标签的FPR(假正率):")
trainingSummary.falsePositiveRateByLabel.zipWithIndex.foreach {
case (rate, label) => println(s"label $label: $rate")
}
println("标签的TPR(真正率):")
trainingSummary.truePositiveRateByLabel.zipWithIndex.foreach {
case (rate, label) => println(s"label $label: $rate")
}
println("标签的精确度:")
trainingSummary.precisionByLabel.zipWithIndex.foreach {
case (prec, label) => println(s"label $label: $prec")
}
println("标签的召回:")
trainingSummary.recallByLabel.zipWithIndex.foreach {
case (rec, label) => println(s"label $label: $rec")
}
println("标签的F-measure:")
trainingSummary.fMeasureByLabel.zipWithIndex.foreach {
case (f, label) => println(s"label $label: $f")
}
val accuracy = trainingSummary.accuracy
val falsePositiveRate = trainingSummary.weightedFalsePositiveRate
val truePositiveRate = trainingSummary.weightedTruePositiveRate
val fMeasure = trainingSummary.weightedFMeasure
val precision = trainingSummary.weightedPrecision
val recall = trainingSummary.weightedRecall
println(s"Accuracy: $accuracy\nFPR: $falsePositiveRate\nTPR: $truePositiveRate\n" + s"F-measure: $fMeasure\nPrecision: $precision\nRecall: $recall")Python代码:
from pyspark.ml.classification import LogisticRegression
training = spark.read.format("libsvm").load("/sample_multiclass_classification_data.txt")
lr = LogisticRegression(maxIter=10, regParam=0.3, elasticNetParam=0.8)
# Fit the model
lrModel = lr.fit(training)
# Print the coefficients and intercept for multinomial logistic regression
print("Coefficients: \n" + str(lrModel.coefficientMatrix))
print("Intercept: " + str(lrModel.interceptVector))
trainingSummary = lrModel.summary
# Obtain the objective per iteration
objectiveHistory = trainingSummary.objectiveHistory
print("objectiveHistory:")for objective in objectiveHistory:
print(objective)
# for multiclass, we can inspect metrics on a per-label basis
print("False positive rate by label:")
for i, rate in enumerate(trainingSummary.falsePositiveRateByLabel):
print("label %d: %s" % (i, rate))
print("True positive rate by label:")
for i, rate in enumerate(trainingSummary.truePositiveRateByLabel):
print("label %d: %s" % (i, rate))
print("Precision by label:")
for i, prec in enumerate(trainingSummary.precisionByLabel):
print("label %d: %s" % (i, prec))
print("Recall by label:")
for i, rec in enumerate(trainingSummary.recallByLabel):
print("label %d: %s" % (i, rec))
print("F-measure by label:")
for i, f in enumerate(trainingSummary.fMeasureByLabel()):
print("label %d: %s" % (i, f))
accuracy = trainingSummary.accuracy
falsePositiveRate = trainingSummary.weightedFalsePositiveRate
truePositiveRate = trainingSummary.weightedTruePositiveRate
fMeasure = trainingSummary.weightedFMeasure()
precision = trainingSummary.weightedPrecision
recall = trainingSummary.weightedRecall
print("Accuracy: %s\nFPR: %s\nTPR: %s\nF-measure: %s\nPrecision: %s\nRecall: %s" % (accuracy, falsePositiveRate, truePositiveRate, fMeasure, precision, recall))有两种最优化算法可以求解逻辑回归问题并求出最优参数:mini-batch gradient descent(梯度下降法),L-BFGS法。我们更推荐使用L-BFGS,因为它能更快聚合,而且现在spark2.1.0已经放弃LogisticRegressionWithLSGD()模式了.
决策树分类器(DTC)
决策树 及其集合是分类和回归机器学习算法中的流行方法,属于判别模型。主要的决策树算法有ID3、C4.5(C5.0)、CART(分类与回归树)、PUBLIC、SLIQ和SPRINT算法等。它们在选择测试属性采用的技术、生成的决策树的结构、剪枝的方法以及时刻,能否处理大数据集等方面都有各自的不同之处。
分类树的映射函数是多维空间的分段线性划分,即用平行于各坐标轴的超平面对空间进行切分;回归树的映射函数是分段常数函数。分类树和回归树均属于二叉决策树。预测时从根节点开始,每次只对一个特征进行判定,然后进入左子节点或右子节点,直到到达一个叶子节点(表示最终的决策结果,它们没有子节点)处,得到类别值或回归函数值。预测算法的时间复杂度与树的深度有关,判定的执行次数不超过决策树的深度。
有关spark.ml实施的更多信息可以在下文决策树部分中找到。
例子:以LibSVM格式加载数据集,将其拆分为训练集和测试集,在第一个数据集上训练,然后在保留的测试集上进行评估。我们使用两个特征变换器来准备数据; 这些帮助标记和分类特征的索引类别,将DataFrame决策树算法可识别的元数据添加到其中。
Scala代码:
import org.apache.spark.ml.Pipeline
import org.apache.spark.ml.classification.DecisionTreeClassificationModel
import org.apache.spark.ml.classification.DecisionTreeClassifier
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator
import org.apache.spark.ml.feature.{IndexToString, StringIndexer, VectorIndexer}
// 加载以LIBSVM格式存储的数据作为Dataframe.
val data = spark.read.format("libsvm").load("/libsvm_data.txt")
// 索引标签,向标签列添加元数据.适用于整个数据集,以包括所有标签的索引.
val labelIndexer = new StringIndexer()
.setInputCol("label")
.setOutputCol("indexedLabel")
.fit(data)
// 自动识别分类特征,并对它们进行索引.
val featureIndexer = new VectorIndexer()
.setInputCol("features")
.setOutputCol("indexedFeatures")
.setMaxCategories(4) // 具有大于4个不同值的特征被视为连续的.
.fit(data)
// 将数据划分为训练和测试集(70%用于训练,30%用于测试)
val Array(trainingData, testData) = data.randomSplit(Array(0.7, 0.3))
// 训练决策树模型.
val dt = new DecisionTreeClassifier()
.setLabelCol("indexedLabel")
.setFeaturesCol("indexedFeatures")
// 将索引标签转换回原始标签.
val labelConverter = new IndexToString()
.setInputCol("prediction")
.setOutputCol("predictedLabel")
.setLabels(labelIndexer.labels)
// 链索引器和管道中的树.
val pipeline = new Pipeline().setStages(Array(labelIndexer, featureIndexer, dt, labelConverter))
// 训练模型。这也运行索引器.
val model = pipeline.fit(trainingData)
// 作出预测.
val predictions = model.transform(testData)
// 选择要显示的示例行.
predictions.select("predictedLabel", "label", "features").show(5)
// 选择(预测,真实标签)并计算测试误差.
val evaluator = new MulticlassClassificationEvaluator()
.setLabelCol("indexedLabel")
.setPredictionCol("prediction")
.setMetricName("accuracy")
val accuracy = evaluator.evaluate(predictions)
println(s"Test Error = ${(1.0 - accuracy)}")
val treeModel = model.stages(2).asInstanceOf[DecisionTreeClassificationModel]
println(s"Learned classification tree model:\n ${treeModel.toDebugString}")Java代码:
import org.apache.spark.ml.Pipeline;
import org.apache.spark.ml.PipelineModel;
import org.apache.spark.ml.PipelineStage;
import org.apache.spark.ml.classification.DecisionTreeClassifier;
import org.apache.spark.ml.classification.DecisionTreeClassificationModel;
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator;
import org.apache.spark.ml.feature.*;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;
Dataset data = spark.read().format("libsvm").load("/libsvm_data.txt");
StringIndexerModel labelIndexer = new StringIndexer()
.setInputCol("label")
.setOutputCol("indexedLabel")
.fit(data);
VectorIndexerModel featureIndexer = new VectorIndexer()
.setInputCol("features")
.setOutputCol("indexedFeatures")
.setMaxCategories(4) //具有大于4个不同值的特征被视为连续的.
.fit(data);
Dataset[] splits = data.randomSplit(new double[]{0.7, 0.3});
Dataset trainingData = splits[0];
Dataset testData = splits[1];
DecisionTreeClassifier dt = new DecisionTreeClassifier()
.setLabelCol("indexedLabel")
.setFeaturesCol("indexedFeatures");
IndexToString labelConverter = new IndexToString()
.setInputCol("prediction")
.setOutputCol("predictedLabel")
.setLabels(labelIndexer.labels());
Pipeline pipeline = new Pipeline().setStages(new PipelineStage[]{labelIndexer, featureIndexer, dt, labelConverter});
PipelineModel model = pipeline.fit(trainingData);
Dataset predictions = model.transform(testData);
predictions.select("predictedLabel", "label", "features").show(5);
MulticlassClassificationEvaluator evaluator = new MulticlassClassificationEvaluator()
.setLabelCol("indexedLabel")
.setPredictionCol("prediction")
.setMetricName("accuracy");
double accuracy = evaluator.evaluate(predictions);
System.out.println("Test Error = " + (1.0 - accuracy));
DecisionTreeClassificationModel treeModel =
(DecisionTreeClassificationModel) (model.stages()[2]);
System.out.println("Learned classification tree model:\n" + treeModel.toDebugString());
随机森林分类器(RFC)
随机森林(Random forest) 是决策树集合,结合了许多决策树,以降低过度拟合的风险,并且其输出的类别是由个别树输出的类别的众数而定。有关spark.ml实施的更多信息可以在随机森林部分中找到。
例子:以下示例以LibSVM格式加载数据集,将其拆分为训练集和测试集,在第一个数据集上训练,然后在保留的测试集上进行评估。我们使用两个特征变换器来准备数据; 这些帮助标记和分类特征的索引类别,将元数据添加到基于树的算法可以识别的DataFrame中。
Scala代码:
import org.apache.spark.ml.Pipeline
import org.apache.spark.ml.classification.{RandomForestClassificationModel, RandomForestClassifier}
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator
import org.apache.spark.ml.feature.{IndexToString, StringIndexer, VectorIndexer}
// 加载并解析数据文件,将其转换为DataFrame.
val data = spark.read.format("libsvm").load("/libsvm_data.txt")
// 索引标签,向标签列添加元数据.
val labelIndexer = new StringIndexer()
.setInputCol("label")
.setOutputCol("indexedLabel")
.fit(data)
// 自动识别分类特征,并对它们进行索引.
//设置maxCategories,使具有> 4个不同值的特征被视为连续的.
val featureIndexer = new VectorIndexer()
.setInputCol("features")
.setOutputCol("indexedFeatures")
.setMaxCategories(4)
.fit(data)
// 将数据划分为训练和测试集(70%用于训练,30%用于测试).
val Array(trainingData, testData) = data.randomSplit(Array(0.7, 0.3))
// Train a RandomForest model.
val rf = new RandomForestClassifier()
.setLabelCol("indexedLabel")
.setFeaturesCol("indexedFeatures")
.setNumTrees(10) //需要训练的树的数量(默认值:20)
// 将索引标签转换回原始标签.
val labelConverter = new IndexToString()
.setInputCol("prediction")
.setOutputCol("predictedLabel")
.setLabels(labelIndexer.labels)
// 链索引器和管道中的forest.
val pipeline = new Pipeline().setStages(Array(labelIndexer, featureIndexer, rf, labelConverter))
// 训练模型。这也运行索引器.
val model = pipeline.fit(trainingData)
// 作出预测.
val predictions = model.transform(testData)
// 选择要显示的示例行.
predictions.select("predictedLabel", "label", "features").show(5)
// 选择(预测,真实标签)并计算测试误差.
val evaluator = new MulticlassClassificationEvaluator()
.setLabelCol("indexedLabel")
.setPredictionCol("prediction")
.setMetricName("accuracy") //求值中度量名称的参数(支持"f1"(默认),"weightedPrecision",“weightedRecall”,“accuracy”)
val accuracy = evaluator.evaluate(predictions)
println(s"精确率 = ${accuracy}")
val rfModel = model.stages(2).asInstanceOf[RandomForestClassificationModel]
println(s"学习分类森林模型:\n ${rfModel.toDebugString}")Java代码:
import org.apache.spark.ml.Pipeline;
import org.apache.spark.ml.PipelineModel;
import org.apache.spark.ml.PipelineStage;
import org.apache.spark.ml.classification.RandomForestClassificationModel;
import org.apache.spark.ml.classification.RandomForestClassifier;
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator;
import org.apache.spark.ml.feature.*;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;
Dataset data = spark.read().format("libsvm").load("/libsvm_data.txt");
// 索引标签,向标签列添加元数据.适用于整个数据集,以包括所有标签的索引
StringIndexerModel labelIndexer = new StringIndexer().setInputCol("label").setOutputCol("indexedLabel").fit(data);
VectorIndexerModel featureIndexer = new VectorIndexer().setInputCol("features").setOutputCol("indexedFeatures").setMaxCategories(4).fit(data);
Dataset[] splits = data.randomSplit(new double[] {0.7, 0.3});
Dataset trainingData = splits[0];
Dataset testData = splits[1];
RandomForestClassifier rf = new RandomForestClassifier()
.setLabelCol("indexedLabel")
.setFeaturesCol("indexedFeatures");
IndexToString labelConverter = new IndexToString()
.setInputCol("prediction")
.setOutputCol("predictedLabel")
.setLabels(labelIndexer.labels());
Pipeline pipeline = new Pipeline().setStages(new PipelineStage[] {labelIndexer, featureIndexer, rf, labelConverter});
PipelineModel model = pipeline.fit(trainingData);
Dataset predictions = model.transform(testData);
predictions.select("predictedLabel", "label", "features").show(5);
MulticlassClassificationEvaluator evaluator = new MulticlassClassificationEvaluator()
.setLabelCol("indexedLabel")
.setPredictionCol("prediction")
.setMetricName("accuracy");
double accuracy = evaluator.evaluate(predictions);
System.out.println("Test Error = " + (1.0 - accuracy));
RandomForestClassificationModel rfModel = (RandomForestClassificationModel)(model.stages()[2]);
System.out.println("Learned classification forest model:\n" + rfModel.toDebugString());
梯度提升树分类器(GBTC)
梯度提升树(Gradient-boosted tree, GBT或GBDT)是使用决策树集合的流行分类和回归方法。梯度提升树(GBT) 是决策树的集合。GBT迭代地训练决策树以最小化损失函数。样本输出不是连续的值,而是离散的类别。该spark.ml实现支持使用连续和分类特征进行二进制分类和回归的GBT。
有关spark.ml实施的更多信息请参见下文GBT部分。
更多GBT介绍参见:https://www.cnblogs.com/pinard/p/6140514.html
例子:以下示例以LibSVM格式加载数据集,将其拆分为训练集和测试集,在第一个数据集上训练,然后在保留的测试集上进行评估。我们使用两个特征变换器来准备数据; 这些帮助标记和分类特征的索引类别,向DataFrame基于树的算法可以识别的元数据添加元数据。
Scala代码:
import org.apache.spark.ml.Pipeline
import org.apache.spark.ml.classification.{GBTClassificationModel, GBTClassifier}
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator
import org.apache.spark.ml.feature.{IndexToString, StringIndexer, VectorIndexer}
// 加载并解析数据文件,将其转换为DataFrame.
val data = spark.read.format("libsvm").load("data/mllib/libsvm_data.txt")
// 索引标签,向标签列添加元数据.:适用于整个数据集,以包括所有标签的索引
val labelIndexer = new StringIndexer()
.setInputCol("label")
.setOutputCol("indexedLabel")
.fit(data)
// 自动识别分类特征,并对它们进行索引.
// 设置maxCategories,使具有> 4个不同值的特性被视为连续的.
val featureIndexer = new VectorIndexer()
.setInputCol("features")
.setOutputCol("indexedFeatures")
.setMaxCategories(4)
.fit(data)
// 将数据划分为训练和测试集(70%用于训练,30%用于测试).
val Array(trainingData, testData) = data.randomSplit(Array(0.7, 0.3))
// 训练GBT模型
val gbt = new GBTClassifier()
.setLabelCol("indexedLabel")
.setFeaturesCol("indexedFeatures")
.setMaxIter(10)
.setFeatureSubsetStrategy("auto")
// 将索引标签转换回原始标签.
val labelConverter = new IndexToString()
.setInputCol("prediction")
.setOutputCol("predictedLabel")
.setLabels(labelIndexer.labels)
// 链索引器和GBT在管道中.
val pipeline = new Pipeline().setStages(Array(labelIndexer, featureIndexer, gbt, labelConverter))
// 训练模型。这也运行索引器.
val model = pipeline.fit(trainingData)
// 作出预测.
val predictions = model.transform(testData)
// 选择要显示的示例行.
predictions.select("predictedLabel", "label", "features").show(5)
// 选择(预测,真实标签)并计算测试误差.
val evaluator = new MulticlassClassificationEvaluator()
.setLabelCol("indexedLabel")
.setPredictionCol("prediction")
.setMetricName("accuracy")
val accuracy = evaluator.evaluate(predictions)
println(s"Test Error = ${1.0 - accuracy}")
val gbtModel = model.stages(2).asInstanceOf[GBTClassificationModel]
println(s"Learned classification GBT model:\n ${gbtModel.toDebugString}")Java代码:
import org.apache.spark.ml.Pipeline;
import org.apache.spark.ml.PipelineModel;
import org.apache.spark.ml.PipelineStage;
import org.apache.spark.ml.classification.GBTClassificationModel;
import org.apache.spark.ml.classification.GBTClassifier;
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator;
import org.apache.spark.ml.feature.*;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;
Dataset data = spark.read().format("libsvm").load("data/mllib/libsvm_data.txt");
//索引标签,向标签列添加元数据。适用于整个数据集,在索引中包含所有标签。
StringIndexerModel labelIndexer = new StringIndexer()
.setInputCol("label")
.setOutputCol("indexedLabel")
.fit(data);
//自动识别分类特征,并对它们进行索引。
//设置maxCategories,使具有> 4个不同值的特性被视为连续的。
VectorIndexerModel featureIndexer = new VectorIndexer()
.setInputCol("features")
.setOutputCol("indexedFeatures")
.setMaxCategories(4)
.fit(data);
// 将数据划分为训练和测试集(70%用于训练,30%用于测试)
Dataset[] splits = data.randomSplit(new double[] {0.7, 0.3});
Dataset trainingData = splits[0];
Dataset testData = splits[1];
GBTClassifier gbt = new GBTClassifier()
.setLabelCol("indexedLabel")
.setFeaturesCol("indexedFeatures")
.setMaxIter(10);
IndexToString labelConverter = new IndexToString()
.setInputCol("prediction")
.setOutputCol("predictedLabel")
.setLabels(labelIndexer.labels());
Pipeline pipeline = new Pipeline().setStages(new PipelineStage[] {labelIndexer, featureIndexer, gbt, labelConverter});
PipelineModel model = pipeline.fit(trainingData);
Dataset predictions = model.transform(testData);
// 选择要显示的示例行.
predictions.select("predictedLabel", "label", "features").show(5);
// 选择(预测,真实标签)并计算测试误差。
MulticlassClassificationEvaluator evaluator = new MulticlassClassificationEvaluator()
.setLabelCol("indexedLabel")
.setPredictionCol("prediction")
.setMetricName("accuracy");
double accuracy = evaluator.evaluate(predictions);
System.out.println("Test Error = " + (1.0 - accuracy));
GBTClassificationModel gbtModel = (GBTClassificationModel)(model.stages()[2]);
System.out.println("Learned classification GBT model:\n" + gbtModel.toDebugString());
多层感知器分类器(MLPC)
多层感知器分类器(Multilayer perceptron classifier,MLPC)是一种基于前馈人工神经网络的分类器。MLPC由多层节点组成。每一层都与网络中的下一层完全连接。输入层中的节点表示输入数据。所有其他节点通过输入与节点权重w和偏差b的线性组合并应用一个激活函数将输入映射到输出。对于K+1层的MLPC,可以用矩阵形式表示如下:
![]()
中间层节点使用sigmoid (logistic)函数:
输出层节点使用softmax函数:
输出层中节点N的数量对应于类的数量。
MLPC采用反向传播学习模型,使用逻辑损失函数进行优化,并将L-BFGS作为优化例程。
Scala代码:
import org.apache.spark.ml.classification.MultilayerPerceptronClassifier
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator
// 加载以LIBSVM格式存储的数据作为DataFrame.
val data = spark.read.format("libsvm").load("data/mllib/multiclass_data.txt")
// 将数据分解为训练和测试
val splits = data.randomSplit(Array(0.6, 0.4), seed = 1234L)
val train = splits(0)
val test = splits(1)
// 为神经网络指定层:输入层为4(特征),两个中间层为5和4,输出层为3(类)
val layers = Array[Int](4, 5, 4, 3)
// 创建训练器并设置其参数
val trainer = new MultilayerPerceptronClassifier()
.setLayers(layers)
.setBlockSize(128)
.setSeed(1234L)
.setMaxIter(100)
// 训练模型
val model = trainer.fit(train)
// 在测试集上计算精度
val result = model.transform(test)
val predictionAndLabels = result.select("prediction", "label")
val evaluator = new MulticlassClassificationEvaluator().setMetricName("accuracy")
println(s"测试集的准确率 = ${evaluator.evaluate(predictionAndLabels)}")Java代码:
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;
import org.apache.spark.ml.classification.MultilayerPerceptronClassificationModel;
import org.apache.spark.ml.classification.MultilayerPerceptronClassifier;
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator;
String path = "/multiclass_classification_data.txt";
Dataset dataFrame = spark.read().format("libsvm").load(path);
Dataset[] splits = dataFrame.randomSplit(new double[]{0.6, 0.4}, 1234L);
Dataset train = splits[0];
Dataset test = splits[1];
int[] layers = new int[] {4, 5, 4, 3};
MultilayerPerceptronClassifier trainer = new MultilayerPerceptronClassifier()
.setLayers(layers)
.setBlockSize(128)
.setSeed(1234L)
.setMaxIter(100);
MultilayerPerceptronClassificationModel model = trainer.fit(train);
Dataset result = model.transform(test);
Dataset predictionAndLabels = result.select("prediction", "label");
MulticlassClassificationEvaluator evaluator = new MulticlassClassificationEvaluator().setMetricName("accuracy");
System.out.println("Test set accuracy = " + evaluator.evaluate(predictionAndLabels));
线性支持向量机(SVM)
支持向量机(Support Vector Machine, SVM)是一类按监督学习方式对数据进行二元分类的广义线性分类器(generalized linear classifier),其决策边界是对学习样本求解的最大边距超平面(maximum-margin hyperplane),属于判别模型。它在高维或无限维空间中构造超平面或超平面集合,可用于分类、回归或其他任务。从直观上看,对于任意类,距离最近的训练数据点最大的超平面(即所谓的泛函边距)都可以实现很好的分离,因为一般来说,边距越大,分类器的泛化误差就越小。Spark ML中的linear svc支持使用线性SVM进行二分类。在内部,它使用OWLQN优化器对铰链损耗进行优化。
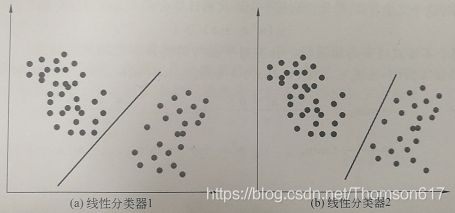
如下图所示,两条直线都可以将两类样本分开:
问题是:在多个可行的线性分类器中,什么样的分类器是好的?从直观上看,为了得到好的泛化性能,分类平面应该不偏向于任何一类,并且离两个类的样本都尽可能远。这种最大化分类间隔的目标就是支持向量机的基本思想。目前,线性支持向量机因为计算速度快,被用于行人检测、文本分类等问题。
例子
Scala代码:
import org.apache.spark.ml.classification.LinearSVC
val training = spark.read.format("libsvm").load("/libsvm_data.txt")
val lsvc = new LinearSVC()
.setMaxIter(10)
.setRegParam(0.1)
// Fit the model
val lsvcModel = lsvc.fit(training)
// 打印线性svc的系数和截距
println(s"系数: ${lsvcModel.coefficients} 截距: ${lsvcModel.intercept}")Pathon示例(python 3环境下使用scikit-learn封装模块的SVM编程实现):
# 导入模块
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
% matplotlib inline
# 加载数据
iris = datasets.load_iris()
X = iris.data[:, :2] # 为便于绘图仅选择2个特征
y = iris.target
# 测试样本(绘制分类区域)
xlist1 = np.linspace(X[:, 0].min(), X[:, 0].max(), 200)
xlist2 = np.linspace(X[:, 1].min(), X[:, 1].max(), 200)
XGrid1, XGrid2 = np.meshgrid(xlist1, xlist2)
# 非线性SVM:RBF核,超参数为0.5,正则化系数为1,SMO迭代精度1e-5, 内存占用1000MB
svc = svm.SVC(kernel='rbf', C=1, gamma=0.5, tol=1e-5, cache_size=1000).fit(X, y)
# 预测并绘制结果
Z = svc.predict(np.vstack([XGrid1.ravel(), XGrid2.ravel()]).T)
Z = Z.reshape(XGrid1.shape)
plt.contourf(XGrid1, XGrid2, Z, cmap=plt.cm.hsv)
plt.contour(XGrid1, XGrid2, Z, colors=('k',))
plt.scatter(X[:,0], X[:,1], c=y, edgecolors='k', linewidth=1.5, cmap=plt.cm.hsv)One-vs-Rest分类器
OneVsRest(又名One-vs-All,二元分类器)是一个用于执行多类分类的机器学习约简的例子,给出了一个能够有效执行二进制分类的基分类器。它也被称为“一对多模式”。
OneVsRest实现为Estimator。对于基本分类器,它接受实例Classifier并为每个k类创建二进制分类问题。训练i类的分类器来预测标签是否为i,将类i与所有其他类区分开来。
通过评估每个二元分类器来完成预测,并且将最自信的分类器的索引输出为标签。
例子:下面的示例演示了如何加载 Iris数据集,将其解析为DataFrame并使用执行多类分类OneVsRest。计算测试误差以测量算法精度。
Scala代码:
import org.apache.spark.ml.classification.{LogisticRegression, OneVsRest}
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator
// load data file.
val inputData = spark.read.format("libsvm").load("data/mllib/sample_multiclass_classification_data.txt")
val Array(train, test) = inputData.randomSplit(Array(0.8, 0.2))
// 实例化基础分类器
val classifier = new LogisticRegression()
.setMaxIter(10)
.setTol(1E-6)
.setFitIntercept(true)
// 实例化One Vs Rest分类器.
val ovr = new OneVsRest().setClassifier(classifier)
// 训练多级模型.
val ovrModel = ovr.fit(train)
// 根据测试数据对模型进行评分.
val predictions = ovrModel.transform(test)
// 获得评估者.
val evaluator = new MulticlassClassificationEvaluator().setMetricName("accuracy")
// 计算测试数据的分类误差.
val accuracy = evaluator.evaluate(predictions)
println(s"Test Error = ${1 - accuracy}")Java代码:
import org.apache.spark.ml.classification.LogisticRegression;
import org.apache.spark.ml.classification.OneVsRest;
import org.apache.spark.ml.classification.OneVsRestModel;
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
Dataset inputData = spark.read().format("libsvm").load("/sample_multiclass_classification_data.txt");
Dataset[] tmp = inputData.randomSplit(new double[]{0.8, 0.2});
Dataset train = tmp[0];
Dataset test = tmp[1];
LogisticRegression classifier = new LogisticRegression()
.setMaxIter(10)
.setTol(1E-6)
.setFitIntercept(true);
OneVsRest ovr = new OneVsRest().setClassifier(classifier);
OneVsRestModel ovrModel = ovr.fit(train);
Dataset predictions = ovrModel.transform(test).select("prediction", "label");
MulticlassClassificationEvaluator evaluator = new MulticlassClassificationEvaluator().setMetricName("accuracy");
double accuracy = evaluator.evaluate(predictions);
System.out.println("Test Error = " + (1 - accuracy));
朴素贝叶斯(NB)
朴素贝叶斯(Naive Bayes)是一种基于贝叶斯定理和特征条件独立假设的分类方法(利用概率统计知识进行分类),属于生成模型。朴素贝叶斯模型本质上就是一个概率表,其通过训练数据更新这张表中的概率。为了预测一个新的观察值,朴素贝叶斯算法就是根据样本的特征值在概率表中寻找最大概率的那个类别。具体应用包括垃圾邮件分类问题、自然语言处理中的文本分类问题、智能视频监控中的背景建模算法、人脸识别中的联合贝叶斯模型等等。
在某个事件已经发生的情况下,为了计算出另一个相同事件发生的概率,我们使用贝叶斯定理。根据某些变量的给定值,要想计算某个结果的概率,也就是根据我们的已知知识(d)计算假设(h)为真的概率,我们这样使用贝叶斯定理:
P(h|d)= ( P(d|h) * P(h) ) / P(d)
其中:
P(h|d) =后验概率。假设h的概率为真,给定数据为d,那么: P(h|d)= P(d1| h)* P(d2| h)*....*P(dn| h)* P(d)
P(d|h) =可能性。假设h为真时, d发生的概率。
P(h) = 类的先验概率。假设h的概率为真(不管数据d的情况)。
P(d) = Predictor 的先验概率。数据d的概率(不管假设h的情况)。
这种算法之所以被称为「朴素」,是因为它假定所有的变量(特征条件)之间相互独立(独立性假设),而这种假设在实际应用往往不成立。如果假设特征向量服从多维正态分布,则为正态贝叶斯分类器。
朴素贝叶斯分类器是一类简单的概率多类分类器,它基于应用贝叶斯定理,在每对特征之间具有强(天真)独立假设。通过对训练数据的单次传递,它计算给定每个标签的每个特征的条件概率分布,可以非常有效地训练。对于预测,它应用贝叶斯定理来计算给定观察的每个标签的条件概率分布。
MLlib支持多项式朴素贝叶斯 和伯努利朴素贝叶斯。
输入数据:这些模型通常用于文档分类。在该上下文中,每个观察是一个文档,每个特征代表一个术语。特征值是术语的频率(在多项式朴素贝叶斯中)或零或一个,表示该术语是否在文档中找到(在伯努利朴素贝叶斯中)。要素值必须为非负值。使用可选参数“multinomial”或“bernoulli”选择模型类型,默认为“multinomial”。对于文档分类,输入特征向量通常应该是稀疏向量。由于训练数据仅使用一次,因此不必对其进行缓存。
通过设置参数λ可以使用加法平滑λ(默认为1.0)。
优点:即使条件独立性假设很难成立,但朴素贝叶斯算法在实践中表现出乎意料地好。该算法很容易实现并能随数据集的更新而扩展。
缺点:因为朴素贝叶斯算法太简单,所以其也经常被以上列出的分类算法所替代。
例子:
Scala代码:
import org.apache.spark.ml.classification.NaiveBayes
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator
// 加载以LIBSVM格式存储的数据作为DataFrame.
val data = spark.read.format("libsvm").load("/libsvm_data.txt")
// 将数据划分为训练和测试集(70%用于训练,30%用于测试)
val Array(trainingData,testData)=data.randomSplit(Array(0.7,0.3),seed=1234L)
// Train a NaiveBayes model.
val model = new NaiveBayes().fit(trainingData)
// 选择要显示的示例行.
val predictions = model.transform(testData)
predictions.show()
// 选择(预测,真实标签)并计算测试误差
val evaluator = new MulticlassClassificationEvaluator()
.setLabelCol("label")
.setPredictionCol("prediction")
.setMetricName("accuracy")
val accuracy = evaluator.evaluate(predictions)
println(s"Test set accuracy = $accuracy")Java代码:
import org.apache.spark.ml.classification.NaiveBayes;
import org.apache.spark.ml.classification.NaiveBayesModel;
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;
Dataset dataFrame =spark.read().format("libsvm").load("/libsvm_data.txt");
Dataset[] splits = dataFrame.randomSplit(new double[]{0.6, 0.4}, 1234L);
Dataset train = splits[0];
Dataset test = splits[1];
NaiveBayes nb = new NaiveBayes();
NaiveBayesModel model = nb.fit(train);
Dataset predictions = model.transform(test);
predictions.show();
MulticlassClassificationEvaluator evaluator = new MulticlassClassificationEvaluator()
.setLabelCol("label")
.setPredictionCol("prediction")
.setMetricName("accuracy");
double accuracy = evaluator.evaluate(predictions);
System.out.println("Test set accuracy = " + accuracy);
6.2回归(Regression)
回归方法是一种对数值型连续随机变量进行预测和建模的监督学习算法。回归的目的是预测数值型的目标值。最直接的办法是依据输入写出一个目标值的计算公式,该公式就是所谓的回归方程(regression equation)。求回归方程中的回归系数的过程就是回归。
回归任务的特点是标注的数据集具有数值型的目标变量。也就是说,每一个观察样本都有一个数值型的标注真值以监督算法。
回归算法主要用来进行连续值的预测,譬如房价预测、股票走势、测试成绩、网站PV、明天气温多少度,PM2.5有多少,广告的投入与市场销售的关系,受教育程度与收入的关系,等等。
回归问题的条件/前提:
1)收集的数据
2)假设的模型,即一个函数,这个函数里含有未知的参数,通过学习,可以估计出参数。然后利用这个模型去预测/分类新的数据。
对于回归问题,评价指标是回归误差,定义为预测函数输出值与样本标签值之间的均方误差。
线性回归(LR)
线性回归(linear regression)意味着可以将输入项分别乘以一些常量,再将结果加起来得到输出。该算法的形式十分简单,它期望使用一个超平面拟合数据集(只有两个变量的时候就是一条直线)。如果数据集中的变量存在线性关系,那么其就能拟合地非常好。线性回归输出连续值,而类别标签只有0、1两个,所以需要人为设定一个阈值,将输出值与该值比较大小,从而来判断模型将样本分到哪一类,而这个阈值会受到离群点(outlier)的牵制,因为线性回归的拟合曲线会因为离群点而受到较大影响。
线性回归的一个问题是有可能出现欠拟合现象,因为它求的是具有最小均方误差的无偏估计。为了降低预测的均方误差,可以在估计中引入一些偏差,其中一个方法是局部加权线性回归(Locally Weighted Linear Regression, LWLR)。如果数据的特征比样本点还多,也就是说输入数据的矩阵X不是满秩矩阵,非满秩矩阵在求逆时会出现问题。为了解决这个问题,可以使用岭回归(ridge regression)、lasso法、前向逐步回归。
使用线性回归模型和模型摘要的界面类似于逻辑回归案例。
当通过“l-bfgs”求解器对具有常量非零列的数据集进行无截距拟合LinearRegressionModel时,Spark MLlib为常量非零列输出零系数。此行为与R glmnet相同,但与LIBSVM(支持向量机)不同。
例子:
以下示例演示了训练正则化线性回归模型和提取模型汇总统计量。
Scala代码:
import org.apache.spark.ml.regression.LinearRegression
// Load training data
val training = spark.read.format("libsvm").load("/linear_regression.txt")
val lr = new LinearRegression()
.setMaxIter(10)
.setRegParam(0.3)
.setElasticNetParam(0.8)
// Fit the model
val lrModel = lr.fit(training)
// 打印系数和截距进行线性回归
println(s"系数: ${lrModel.coefficients} 截距: ${lrModel.intercept}")
// 在训练集上总结模型并输出一些度量
val summary = lrModel.summary
println(s"迭代次数: ${summary.totalIterations}")
println(s"objectiveHistory:[${summary.objectiveHistory.mkString(",")}]")
trainingSummary.residuals.show()
println(s"RMSE: ${summary.rootMeanSquaredError}")
println(s"r2: ${summary.r2}")Java代码:
import org.apache.spark.ml.regression.LinearRegression;
import org.apache.spark.ml.regression.LinearRegressionModel;
import org.apache.spark.ml.regression.LinearRegressionTrainingSummary;
import org.apache.spark.ml.linalg.Vectors;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;
Dataset training = spark.read().format("libsvm").load("/linear_regression.txt");
LinearRegression lr = new LinearRegression().setMaxIter(10).setRegParam(0.3).setElasticNetParam(0.8);
LinearRegressionModel lrModel = lr.fit(training);
// 打印系数和截距进行线性回归.
System.out.println("Coefficients: "+ lrModel.coefficients() + " Intercept: " + lrModel.intercept());
//在训练集上总结模型并输出一些度量.
LinearRegressionTrainingSummary summary = lrModel.summary();
System.out.println("numIterations: " + summary .totalIterations());
System.out.println("objectiveHistory: " + Vectors.dense(summary.objectiveHistory()));
summary.residuals().show();
System.out.println("RMSE: " + summary.rootMeanSquaredError());
System.out.println("r2: " +summary.r2());
简单的线性回归通常被使用正则化的回归方法(LASSO、Ridge和Elastic-Net)所代替。正则化其实就是一种对过多回归系数采取惩罚以减少过拟合风险的技术。当然,我们还得确定惩罚强度以让模型在欠拟合和过拟合之间达到平衡。
优点:线性回归的理解与解释都十分直观,并且还能通过正则化来降低过拟合的风险。另外,线性模型很容易使用随机梯度下降和新数据更新模型权重。
缺点:线性回归在变量是非线性关系的时候表现很差。并且其也不够灵活以捕捉更复杂的模式,添加正确的交互项或使用多项式很困难并需要大量时间。
广义线性回归(GLR)
与假设输出服从高斯分布的线性回归相比,广义线性模型(GLMs)是响应变量Yi
服从指数族分布的线性模型的规范。Spark的通用线性回归接口允许灵活地指定
GLMs, GLMs可用于各种类型的预测问题,包括线性回归、泊松回归、逻辑回归
等。目前在spark.ml中,只支持指数族分布的一个子集,如下所示。
注意:Spark目前仅通过其GeneralizedLinearRegression 接口支持多达4096个功能,如果超出此约束,则会抛出异常。有关详细信息,请参阅高级部分。尽管如此,对于线性和逻辑回归,可以使用LinearRegression和LogisticRegression估计器训练具有增加的特征数量的模型。
GLMs(Generalized linear model)需要指数族分布,这些分布可以用“canonical”或“natural”形式写成,也就是 自然指数族分布。自然指数族分布的形式如下:(密度函数)
θ称为自然参数,T称为离散参数。在GLM中,假设响应变量Yi由自然指数族分布得到:
![]()
此时自然参数θi与响应变量μi的期望值有关:
![]()
在这里,A’(θi)是由选择分布的形式定义的。glm也允许规范的链接功能,它定义了响应变量μi的期望值和所谓的线性预测ηi之间的关系:
通常,链路选择函数例如![]()
这产生了一个简化的关系感兴趣的参数θ和线性预测η。在这种情况下,关联函数g(μ)据说是“规范”链接功能。
![]()
GLM( 广义线性模型)找到了最大化似然函的回归系数β.
自然参数θi和回归系数β有关联,通过:
![]()
Spark的广义线性回归接口还提供了诊断GLM模型拟合的汇总统计信息,包括残差、p值、偏差、Akaike信息准则等。
有关GLMs及其应用程序的更全面的回顾,请参见此处.
可用的families
例子:如何使用高斯响应和身份链接功能训练GLM并提取模型摘要统计信息:
Scala代码:
import org.apache.spark.ml.regression.GeneralizedLinearRegression
// Load training data
val dataset = spark.read.format("libsvm").load("/linear_regression_data.txt")
val glr = new GeneralizedLinearRegression()
.setFamily("gaussian")
.setLink("identity")
.setMaxIter(10)
.setRegParam(0.3)
// Fit the model
val model = glr.fit(dataset)
// 打印广义线性回归模型的系数和截距
println(s"Coefficients: ${model.coefficients}")
println(s"Intercept: ${model.intercept}")
// 在训练集上总结模型并输出一些度量
val summary = model.summary
println(s"标准误差系数: ${summary.coefficientStandardErrors.mkString(",")}")
println(s"T Values: ${summary.tValues.mkString(",")}")
println(s"P Values: ${summary.pValues.mkString(",")}")
println(s"Dispersion: ${summary.dispersion}")
println(s"Null Deviance: ${summary.nullDeviance}")
println(s"Residual Degree Of Freedom Null: ${summary.residualDegreeOfFreedomNull}")
println(s"Deviance: ${summary.deviance}")
println(s"Residual Degree Of Freedom: ${summary.residualDegreeOfFreedom}")
println(s"AIC: ${summary.aic}")
println("Deviance Residuals: ")summary.residuals().show()Java代码:
import org.apache.spark.sql.Row;
Dataset dataset = spark.read().format("libsvm").load("/linear_regression_data.txt");
GeneralizedLinearRegression glr = new GeneralizedLinearRegression()
.setFamily("gaussian").setLink("identity")
.setMaxIter(10).setRegParam(0.3);
// Fit the model
GeneralizedLinearRegressionModel model = glr.fit(dataset);
// 打印广义线性回归模型的系数和截距
System.out.println("Coefficients: " + model.coefficients());
System.out.println("Intercept: " + model.intercept());
// 在训练集上总结模型并输出一些度量
GeneralizedLinearRegressionTrainingSummary summary = model.summary();
System.out.println("Coefficient Standard Errors: " + Arrays.toString(summary.coefficientStandardErrors()));
System.out.println("T Values: " + Arrays.toString(summary.tValues()));
System.out.println("P Values: " + Arrays.toString(summary.pValues()));
System.out.println("Dispersion: " + summary.dispersion());
System.out.println("Null Deviance: " + summary.nullDeviance());
System.out.println("Residual Degree Of Freedom Null: " + summary.residualDegreeOfFreedomNull());
System.out.println("Deviance: " + summary.deviance());
System.out.println("Residual Degree Of Freedom: " + summary.residualDegreeOfFreedom());
System.out.println("AIC: " + summary.aic());
System.out.println("Deviance Residuals: ");
summary.residuals().show();
决策树回归(DTR)
决策树( Decision Tree)是一种流行的分类和回归方法。有关spark.ml实施的更多信息可以在决策树部分中找到。
例子:以LibSVM格式加载数据集,将其拆分为训练集和测试集,在第一个数据集上训练,然后在保留的测试集上进行评估。我们使用特征变换器来索引分类特征,将DataFrame决策树算法可识别的元数据添加到其中。
Scala代码:
import org.apache.spark.ml.Pipeline
import org.apache.spark.ml.evaluation.RegressionEvaluator
import org.apache.spark.ml.feature.VectorIndexer
import org.apache.spark.ml.regression.DecisionTreeRegressionModel
import org.apache.spark.ml.regression.DecisionTreeRegressor
// Load the data stored in LIBSVM format as a DataFrame.
val data = spark.read.format("libsvm").load("/libsvm_data.txt")
// 自动识别分类特征,并对它们进行索引。这里我们将大于4个不同值的特征视为连续的。
val featureIndexer = new VectorIndexer()
.setInputCol("features")
.setOutputCol("indexedFeatures")
.setMaxCategories(4)
.fit(data)
// 将数据划分为训练和测试集(70%用于训练,30%用于测试).
val Array(trainingData, testData) = data.randomSplit(Array(0.7, 0.3))
// 训练决策树模型.
val dt = new DecisionTreeRegressor().setLabelCol("label").setFeaturesCol("indexedFeatures")
// 链索引器和管道中的树.
val pipeline = new Pipeline().setStages(Array(featureIndexer, dt))
// Train model. This also runs the indexer.
val model = pipeline.fit(trainingData)
// Make predictions.
val predictions = model.transform(testData)
// 选择要显示的示例行.
predictions.select("prediction", "label", "features").show(5)
// 选择(预测,真实标签)并计算测试误差.
val evaluator = new RegressionEvaluator()
.setLabelCol("label")
.setPredictionCol("prediction")
.setMetricName("rmse")
val rmse = evaluator.evaluate(predictions)
println(s"Root Mean Squared Error (RMSE) on test data = $rmse")
val treeModel = model.stages(1).asInstanceOf[DecisionTreeRegressionModel]
println(s"Learned regression tree model:\n ${treeModel.toDebugString}")Java代码:
import org.apache.spark.ml.Pipeline;
import org.apache.spark.ml.PipelineModel;
import org.apache.spark.ml.PipelineStage;
import org.apache.spark.ml.evaluation.RegressionEvaluator;
import org.apache.spark.ml.feature.VectorIndexer;
import org.apache.spark.ml.feature.VectorIndexerModel;
import org.apache.spark.ml.regression.DecisionTreeRegressionModel;
import org.apache.spark.ml.regression.DecisionTreeRegressor;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;
Dataset data = spark.read().format("libsvm").load("/libsvm_data.txt");
VectorIndexerModel featureIndexer = new VectorIndexer()
.setInputCol("features")
.setOutputCol("indexedFeatures")
.setMaxCategories(4)
.fit(data);
Dataset[] splits = data.randomSplit(new double[]{0.7, 0.3});
Dataset trainingData = splits[0];
Dataset testData = splits[1];
DecisionTreeRegressor dt = new DecisionTreeRegressor().setFeaturesCol("indexedFeatures");
Pipeline pipeline = new Pipeline().setStages(new PipelineStage[]{featureIndexer, dt});
PipelineModel model = pipeline.fit(trainingData);
Dataset predictions = model.transform(testData);
predictions.select("label", "features").show(5);
RegressionEvaluator evaluator = new RegressionEvaluator()
.setLabelCol("label")
.setPredictionCol("prediction")
.setMetricName("rmse");
double rmse = evaluator.evaluate(predictions);
System.out.println("Root Mean Squared Error (RMSE) on test data = " + rmse);
DecisionTreeRegressionModel treeModel = (DecisionTreeRegressionModel) (model.stages()[1]);
System.out.println("Learned regression tree model:\n" + treeModel.toDebugString());
随机森林回归(RFR)
随机森林(Random forest)是分类和回归方法中常用的一种方法。有关spark.ml实施的更多信息可以在随机森林部分中找到。
例子:
以下示例以LibSVM格式加载数据集,将其拆分为训练集和测试集,在第一个数据集上训练,然后在保留的测试集上进行评估。我们使用特征变换器来索引分类特征,将DataFrame基于树的算法可识别的元数据添加到其中。
Scala代码:
import org.apache.spark.ml.Pipeline
import org.apache.spark.ml.evaluation.RegressionEvaluator
import org.apache.spark.ml.feature.VectorIndexer
import org.apache.spark.ml.regression.{RandomForestRegressionModel, RandomForestRegressor}
// 加载并解析数据文件,将其转换为DataFrame.
val data = spark.read.format("libsvm").load("/libsvm_data.txt")
// 自动识别分类特征,并对它们进行索引。设置maxCategories,将具有大于4个不同值的特性被视为连续的。
val featureIndexer = new VectorIndexer()
.setInputCol("features")
.setOutputCol("indexedFeatures")
.setMaxCategories(4)
.fit(data)
// 将数据划分为训练和测试集(70%用于训练,30%用于测试).
val Array(trainingData, testData) = data.randomSplit(Array(0.7, 0.3))
val rf = new RandomForestRegressor()
.setLabelCol("label")
.setFeaturesCol("indexedFeatures")
// 链索引器和管道中的forest.
val pipeline = new Pipeline().setStages(Array(featureIndexer, rf))
val model = pipeline.fit(trainingData)
// 作出预测.
val predictions = model.transform(testData)
// 选择要显示的示例行.
predictions.select("prediction", "label", "features").show(5)
// 选择(预测,真实标签)并计算测试误差.
val evaluator = new RegressionEvaluator()
.setLabelCol("label")
.setPredictionCol("prediction")
.setMetricName("rmse")
val rmse = evaluator.evaluate(predictions)
println(s"Root Mean Squared Error (RMSE) on test data = $rmse")
val rfModel = model.stages(1).asInstanceOf[RandomForestRegressionModel]
println(s"Learned regression forest model:\n ${rfModel.toDebugString}")Java代码:
import org.apache.spark.ml.Pipeline;
import org.apache.spark.ml.PipelineModel;
import org.apache.spark.ml.PipelineStage;
import org.apache.spark.ml.evaluation.RegressionEvaluator;
import org.apache.spark.ml.feature.VectorIndexer;
import org.apache.spark.ml.feature.VectorIndexerModel;
import org.apache.spark.ml.regression.RandomForestRegressionModel;
import org.apache.spark.ml.regression.RandomForestRegressor;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;
Dataset data = spark.read().format("libsvm").load("/libsvm_data.txt");
VectorIndexerModel featureIndexer = new VectorIndexer()
.setInputCol("features")
.setOutputCol("indexedFeatures")
.setMaxCategories(4)
.fit(data);
Dataset[] splits = data.randomSplit(new double[] {0.7, 0.3});
Dataset trainingData = splits[0];
Dataset testData = splits[1];
RandomForestRegressor rf = new RandomForestRegressor()
.setLabelCol("label")
.setFeaturesCol("indexedFeatures");
Pipeline pipeline = new Pipeline().setStages(new PipelineStage[] {featureIndexer, rf});
PipelineModel model = pipeline.fit(trainingData);
Dataset predictions = model.transform(testData);
predictions.select("prediction", "label", "features").show(5);
RegressionEvaluator evaluator = new RegressionEvaluator()
.setLabelCol("label")
.setPredictionCol("prediction")
.setMetricName("rmse");
double rmse = evaluator.evaluate(predictions);
System.out.println("Root Mean Squared Error (RMSE) on test data = " + rmse);
RandomForestRegressionModel rfModel = (RandomForestRegressionModel)(model.stages()[1]);
System.out.println("Learned regression forest model:\n" + rfModel.toDebugString());
梯度提升树回归(GBDT)
梯度提升(决策)树(Gradient Boosting Decision Tree,GBDT)是使用迭代的决策树集合的流行回归方法,该算法由多棵决策树组成,所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力较强的算法。
GBDT有很多简称,有GBT(Gradient Boosting Tree), GTB(Gradient Tree Boosting ), GBRT(Gradient Boosting Regression Tree), MART(Multiple Additive Regression Tree),其实都是指的同一种算法,本文统一简称GBDT。
GBDT中的树是回归树(不是分类树),GBDT用来做回归预测,调整后也可以用于分类。GBDT的思想使其具有天然优势可以发现多种有区分性的特征以及特征组合。GBDT几乎可用于所有回归问题(线性/非线性)。
GBDT主要的优点:
1) 可以灵活处理各种类型的数据,包括连续值和离散值。
2) 在相对少的调参时间情况下,预测的准确率也可以比较高。这个是相对SVM来说的。
3)使用一些健壮的损失函数,对异常值的鲁棒性非常强。比如Huber损失(Huber损失,它是均方差和绝对损失的折中产物,对于远离中心的异常点,采用绝对损失,而中心附近的点采用均方差。这个界限一般用分位数点度量)函数和Quantile损失函数。
4)和单独使用决策树算法相比,可有效的解决过拟合问题。
GBDT的主要缺点:由于弱学习器之间存在依赖关系,难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。
梯度提升决策树算法如下:
算法步骤解释:
- 1.初始化,估计使损失函数极小化的常数值,它是只有一个根节点的树,即ganma是一个常数值。
- 2.(a)计算损失函数的负梯度在当前模型的值,将它作为残差的估计;
(b)估计回归树叶节点区域,以拟合残差的近似值;
(c)利用线性搜索估计叶节点区域的值,使损失函数极小化;
(d)更新回归树. - 3.得到输出的最终模型 f(x)
例子:(对于此示例,GBTRegressor实际上只需要1次迭代,但通常不会这样):
Scala代码:
import org.apache.spark.ml.Pipeline
import org.apache.spark.ml.evaluation.RegressionEvaluator
import org.apache.spark.ml.feature.VectorIndexer
import org.apache.spark.ml.regression.{GBTRegressionModel, GBTRegressor}
val data = spark.read.format("libsvm").load("/libsvm_data.txt")
// 自动识别分类特征,并对它们进行索引。
// 设置maxCategories,将具有大于4个不同值的特性被视为连续的.
val featureIndexer = new VectorIndexer()
.setInputCol("features")
.setOutputCol("indexedFeatures")
.setMaxCategories(4)
.fit(data)
// 将数据划分为训练和测试集(70%用于训练,30%用于测试).
val Array(trainingData, testData) = data.randomSplit(Array(0.7, 0.3))
// Train a GBT model.
val gbt = new GBTRegressor()
.setLabelCol("label")
.setFeaturesCol("indexedFeatures")
.setMaxIter(10)
// Chain indexer and GBT in a Pipeline.
val pipeline = new Pipeline().setStages(Array(featureIndexer, gbt))
// Train model. This also runs the indexer.
val model = pipeline.fit(trainingData)
// Make predictions.
val predictions = model.transform(testData)
// 选择要显示的示例行.
predictions.select("prediction", "label", "features").show(5)
// 选择(预测,真实标签)并计算测试误差.
val evaluator = new RegressionEvaluator()
.setLabelCol("label")
.setPredictionCol("prediction")
.setMetricName("rmse")
val rmse = evaluator.evaluate(predictions)
println(s"测试数据的均方根误差(RMSE) = $rmse")
val gbtModel = model.stages(1).asInstanceOf[GBTRegressionModel]
println(s"学习回归GBT模型:\n ${gbtModel.toDebugString}")Java代码:
import org.apache.spark.ml.Pipeline;
import org.apache.spark.ml.PipelineModel;
import org.apache.spark.ml.PipelineStage;
import org.apache.spark.ml.evaluation.RegressionEvaluator;
import org.apache.spark.ml.feature.VectorIndexer;
import org.apache.spark.ml.feature.VectorIndexerModel;
import org.apache.spark.ml.regression.GBTRegressionModel;
import org.apache.spark.ml.regression.GBTRegressor;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;
Dataset data = spark.read().format("libsvm").load("/libsvm_data.txt");
//设置maxCategories,将具有大于4个不同值的特性被视为连续的.
VectorIndexerModel featureIndexer = new VectorIndexer()
.setInputCol("features")
.setOutputCol("indexedFeatures")
.setMaxCategories(4)
.fit(data);
Dataset[] splits = data.randomSplit(new double[] {0.7, 0.3});
Dataset trainingData = splits[0];
Dataset testData = splits[1];
GBTRegressor gbt = new GBTRegressor()
.setLabelCol("label").setFeaturesCol("indexedFeatures").setMaxIter(10);
Pipeline pipeline = new Pipeline().setStages(new PipelineStage[] {featureIndexer, gbt});
PipelineModel model = pipeline.fit(trainingData);
Dataset predictions = model.transform(testData);
predictions.select("prediction", "label", "features").show(5);
RegressionEvaluator evaluator = new RegressionEvaluator()
.setLabelCol("label")
.setPredictionCol("prediction")
.setMetricName("rmse");
double rmse = evaluator.evaluate(predictions);
System.out.println("Root Mean Squared Error (RMSE) on test data = " + rmse);
GBTRegressionModel gbtModel = (GBTRegressionModel)(model.stages()[1]);
System.out.println("Learned regression GBT model:\n" + gbtModel.toDebugString());
生存回归(Survival regression)
在spark.ml我们中,我们实现了加速失效时间(AFT) 模型,该模型是用于删失数据的参数生存回归模型。它描述了生存时间对数的模型,因此它通常被称为生存分析的对数线性模型。与为相同目的设计的比例风险模型不同 ,AFT模型更易于并行化,因为每个实例都独立地为目标函数做出贡献。
给定协变量x '的值,对于随机寿命ti( i = 1,…,n),且可能右截尾,AFT模型下的似然函数为:
δi是事件发生的指标即未经审查的。使用![]() 对数似然函数假设形式:
对数似然函数假设形式:
S0(ϵi)是基线幸存者函数,和f0(ϵi)是对应的密度函数。
最常用的AFT模型是基于生存时间的威布尔分布。一生的威布尔分布的极值分布对应于日志的一生,和S0(ϵ)函数是:
![]()
f0(ϵi)函数是:
![]()
寿命为威布尔分布的AFT模型的对数似然函数为:
由于负对数似相当于最小化最大后验概率,我们使用的损失函数优化是−ι(β,σ)。梯度功能β和logσ分别是:
尾模型可以被制定为一个凸优化问题,即找到一个凸函数的最小值的任务−ι(β,σ)取决于β系数向量和日志logσ规模参数。实现的基础优化算法是L-BFGS。实现与R的生存函数survreg的结果匹配
在对非零列不变的数据集进行无截距aft生存性回归模型拟合时,Spark MLlib输出非零列不变的零系数。这种行为不同于R生存::survreg。
例子:
Scala代码:
import org.apache.spark.ml.linalg.Vectors
import org.apache.spark.ml.regression.AFTSurvivalRegression
val training = spark.createDataFrame(Seq(
(1.218, 1.0, Vectors.dense(1.560, -0.605)),
(2.949, 0.0, Vectors.dense(0.346, 2.158)),
(3.627, 0.0, Vectors.dense(1.380, 0.231)),
(0.273, 1.0, Vectors.dense(0.520, 1.151)),
(4.199, 0.0, Vectors.dense(0.795, -0.226)))
).toDF("label", "censor", "features")
val quantileProbabilities = Array(0.3, 0.6)
val aft = new AFTSurvivalRegression()
.setQuantileProbabilities(quantileProbabilities)
.setQuantilesCol("quantiles")
val model = aft.fit(training)
// 打印AFT生存回归的系数、截距和尺度参数
println(s"Coefficients: ${model.coefficients}")
println(s"Intercept: ${model.intercept}")
println(s"Scale: ${model.scale}")
model.transform(training).show(false)Java代码:
import java.util.Arrays;
import java.util.List;
import org.apache.spark.ml.regression.AFTSurvivalRegression;
import org.apache.spark.ml.regression.AFTSurvivalRegressionModel;
import org.apache.spark.ml.linalg.VectorUDT;
import org.apache.spark.ml.linalg.Vectors;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.RowFactory;
import org.apache.spark.sql.SparkSession;
import org.apache.spark.sql.types.DataTypes;
import org.apache.spark.sql.types.Metadata;
import org.apache.spark.sql.types.StructField;
import org.apache.spark.sql.types.StructType;
List data = Arrays.asList(
RowFactory.create(1.218, 1.0, Vectors.dense(1.560, -0.605)),
RowFactory.create(2.949, 0.0, Vectors.dense(0.346, 2.158)),
RowFactory.create(3.627, 0.0, Vectors.dense(1.380, 0.231)),
RowFactory.create(0.273, 1.0, Vectors.dense(0.520, 1.151)),
RowFactory.create(4.199, 0.0, Vectors.dense(0.795, -0.226))
);
StructType schema = new StructType(new StructField[]{
new StructField("label", DataTypes.DoubleType, false, Metadata.empty()),
new StructField("censor", DataTypes.DoubleType, false, Metadata.empty()),
new StructField("features", new VectorUDT(), false, Metadata.empty())
});
Dataset training = spark.createDataFrame(data, schema);
double[] quantileProbabilities = new double[]{0.3, 0.6};
AFTSurvivalRegression aft = new AFTSurvivalRegression()
.setQuantileProbabilities(quantileProbabilities)
.setQuantilesCol("quantiles");
AFTSurvivalRegressionModel model = aft.fit(training);
//打印AFT生存回归的系数、截距和尺度参数
System.out.println("Coefficients: " + model.coefficients());
System.out.println("Intercept: " + model.intercept());
System.out.println("Scale: " + model.scale());
model.transform(training).show(false);
等渗回归(Isotonic regression)
等渗回归属于回归算法族。形式上,等渗回归是一个给定有限实数集Y=y1,y2,…,yn代表观察到的反应和X = x1, x2,…,xn未知响应值拟合找到一个最小化的函数:
以x1≤x2≤…≤xn,其中wi为正权值.得到的函数称为等渗回归,它是唯一的。它可以看作是有序约束下的最小二乘问题。等渗回归本质上是一个拟合原始数据点的单调函数。
我们实现了一个池相邻违反者算法,该算法使用了一种并行等渗回归的方法。训练输入是一个DataFrame,它包含三个列标签、特征和权重。此外,等渗回归算法有一个可选参数,称为等渗,默认为true。这个参数指定了等渗回归是等渗(单调递增)还是反渗(单调递减)。
训练返回一个等渗回归模型,该模型可用于预测已知和未知特征的标签。等渗回归的结果作为分段线性函数处理。因此,预测的规则是:
(1).如果预测输入与训练特性完全匹配,则返回相关的预测。如果有多个具有相同特性的预测,则返回其中一个。哪个是未定义的(与java.util.Arrays.binarySearch相同)。
(2).如果预测输入低于或高于所有训练特征,则分别返回具有最低或最高特征的预测。如果有多个具有相同特性的预测,则分别返回最低或最高。
(3).如果预测输入落在两个训练特征之间,则对预测进行处理。例子:
Scala代码:
import org.apache.spark.ml.regression.IsotonicRegression
val dataset = spark.read.format("libsvm").load("data/mllib/sample_isotonic_regression_libsvm_data.txt")
// Trains an isotonic regression model.
val ir = new IsotonicRegression()
val model = ir.fit(dataset)
println(s"递增边界: ${model.boundaries}\n")
println(s"与边界相关的预测: ${model.predictions}\n")
// Makes predictions.
model.transform(dataset).show()Java代码:
import org.apache.spark.ml.regression.IsotonicRegression;
import org.apache.spark.ml.regression.IsotonicRegressionModel;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
Dataset dataset = spark.read().format("libsvm").load("data/mllib/sample_isotonic_regression_libsvm_data.txt");
IsotonicRegression ir = new IsotonicRegression();
IsotonicRegressionModel model = ir.fit(dataset);
System.out.println("Boundaries in increasing order: " + model.boundaries() + "\n");
System.out.println("Predictions associated with the boundaries: " + model.predictions() + "\n");
model.transform(dataset).show();
6.3线性方法-正则化
SparkML实现了流行的线性方法,如逻辑回归和带有L1(Lasso)或L2(Ridge)正则化范式比的线性最小二乘法。有关实现和调优的详细信息,请参阅基于RDD的API的线性方法指南;这些信息仍然相关。
Zou等人提出的L1和 L2正则化范式比(L1一般用于特征的稀疏化,L2一般用于防止过拟合),通过正则化和变量选择。在数学上,它被定义为L1和 L2正则化的凸组合:
通过适当地设置α,正则化范式比作为特殊情况同时包含L1和 L2正则化。例如,如果一个线性回归模型与弹性训练网络参数α设置为1时,它相当于一个Lasso (套索)模型。另一方面,如果设置为0,α训练模型减少了岭回归(ridge regression)模型。我们实现了线性回归和逻辑回归的管道API与弹性混合正则化。
注意:setElasticNetParam越大表示L1正则所占比例越高,对向量稀疏化效果越好。
如果数据本来就稀疏的情况下,增大setElasticNetParam可能会导致准确率下降!
6.4决策树
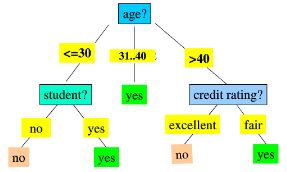
决策树(Decision trees)及其集合是分类和回归方法中的一种流行方法。决策树是由结点和有向边构成的树形结构,从根节点出发,利用特征选择进行分支,最终利用叶子结点的个数以及目标函数的误差约束结束递归的过程。决策树的过程包含特征选择,决策树的生成,决策树的剪枝。决策树被广泛使用,因为它们易于解释,处理分类特征,扩展到多类分类设置,不需要特征缩放,并且能够捕获非线性和特征交互。诸如随机森林和增强的树集合算法是分类和回归任务的最佳表现者。
决策树分为两大类,分类树和回归树。
分类树用于分类标签值,如晴天/阴天/雾/雨、用户性别、网页是否是垃圾页面;
回归树用于预测实数值,如明天的温度、用户的年龄、网页的相关程度;
两者的区别:
- 分类树的结果不能进行加减运算,晴天 晴天没有实际意义;
- 回归树的结果是预测一个数值,可以进行加减运算。
- GBDT 中的决策树是回归树,预测结果是一个数值,在点击率预测方面常用 GBDT,例如用户点击某个内容的概率。
决策树学习是以实例为基础的归纳学习算法,它着眼于从一组无次序、无规则的实例中推理出以决策树表示的分类规则。构造决策树的目的是找出属性和类别间的关系,用它来预测将来未知类别的记录的类别。它采用自顶向下的递归方式,在决策树的内部节点进行属性的比较,并根据不同属性值判断从该节点向下的分支,在决策树的叶节点得到结论。现如今,决策树已被成功地应用于经济和管理数据分析、疾病诊断、模式识别等各类问题。
决策树生成的数学表达式:
决策树是分段线性函数而不是线性函数,它具有非线性建模的能力。只要划分得足够细,分段常数函数可以逼近闭区间上任意函数到任意指定精度,因此,决策树在理论上可以对任意复杂度的数据进行拟合。对于分类问题,如果决策树深度够大,它可以将训练样本集的所有样本正确分类。但如果特征向量维数过高,可能会面临维数灾难导致准确率下降。
该spark.ml实现支持使用连续和分类特征的二进制和多类分类以及回归的决策树。该实现按行对数据进行分区,允许数百万甚至数十亿实例的分布式训练。
用户可以在MLlib决策树指南中找到有关决策树算法的更多信息。此API与原始MLlib Decision Tree API之间的主要区别是:
支持ML管道;
决策树的分离用于分类与回归;
使用DataFrame元数据来区分连续和分类功能.决策树的Pipelines API提供了比原始API更多的功能。特别是,对于分类,用户可以获得每个类的预测概率(也称为类条件概率); 对于回归,用户可以获得有偏差的预测样本方差。
树的组合(随机森林和梯度增强树)在下面的树集合部分中描述。
决策树算法的构建分为3个部分:特征的选择,决策树的生成,决策树的剪枝.
a.特征的选择----选择使信息增益最大的特征;即选择一个分类特征必须是分类确定性更高,此特征才是更好的;
b.决策树的生成---ID3,C4.5算法,此时用迭代的方式构建决策树;注意此时的决策树,因为每次选的都是局部最优解,所以是过拟合的;
c.决策树的剪枝---决策树剪枝是为了防止过拟合,根据全局cost function ,如果剪掉一个数支,cost function 会变小,那么剪掉这个树枝.决策树思想实际上就是寻找最纯净的划分方法,这个最纯净在数学上叫纯度,纯度通俗点理解就是目标变量要分得足够开(y=1的和y=0的混到一起就会不纯)。另一种理解是分类误差率的一种衡量。实际决策树算法往往用到的是,纯度的另一面也即不纯度,下面是不纯度的公式。不纯度的选取有多种方法,每种方法也就形成了不同的决策树方法,比如ID3算法使用信息增益作为不纯度;C4.5算法使用信息增益率作为不纯度;CART算法使用基尼系数作为不纯度。
CART算法:既可以做分类,也可以做回归。只能形成二叉树。
ID3算法:使用信息增益作为分裂的规则,信息增益越大,则选取该分裂规则。多分叉树。信息增益可以理解为,有了x以后对于标签p的不确定性的减少,减少的越多越好,即信息增益越大越好。
C4.5算法:是一个分类决策树算法,使用信息增益率作为分裂规则(需要用信息增益除以,该属性本身的熵),此方法避免了ID3算法中的归纳偏置问题,因为ID3算法会偏向于选择类别较多的属性(形成分支较多会导致信息增益大)。多分叉树。连续属性的分裂只能二分裂,离散属性的分裂可以多分裂,比较分裂前后信息增益率,选取信息增益率最大的。
三种方法对比:
ID3的缺点,倾向于选择水平数量较多的变量,可能导致训练得到一个庞大且深度浅的树;另外输入变量必须是分类变量(连续变量必须离散化);最后无法处理空值。
C4.5选择了信息增益率替代信息增益。
CART以基尼系数替代熵;最小化不纯度而不是最大化信息增益。
输入列(Input Columns)
| 参数名 |
类型 |
默认值 |
说明 |
| labelCol |
Double |
“标签” |
标签预测 |
| featuresCol |
Vector |
“特征” |
特征向量 |
输出列(Output Columns)
| 参数名 |
类型 |
默认 |
描述 |
备注 |
| predictionCol |
Double |
“预测” |
预测标签 |
|
| rawPredictionCol |
Vector |
“rawPrediction” |
向量长度#类别,用于预测树节点上的训练实例标签数量 |
仅限分类 |
| probabilityCol |
Vector |
“可能性” |
向量长度#类别等于rawPrediction归一化为多项分布 |
仅限分类 |
| varianceCol |
Double |
|
预测的偏差样本方差 |
仅回归 |
我们在此列出输入和输出(预测)列类型。所有输出列都是可选的; 要排除输出列,请将其对应的Param设置为空字符串。
6.5树集合(Tree Ensembles)
DataFrame API支持两种主要的树集合算法:随机森林和梯度提升树(GBT)。两者都使用spark.ml决策树作为基础模型。
用户可以在MLlib Ensemble指南中找到有关集合算法的更多信息。
在本节中,我们将演示用于集合的DataFrame API。
此API与原始MLlib合奏API之间的主要区别是:
- 支持DataFrames和ML Pipelines
- 分类与回归的分离
- 使用DataFrame元数据来区分连续和分类功能
- 随机森林的更多功能:特征重要性的估计,以及用于分类的每个类的预测概率。
随机森林(Random forest)
随机森林是决策树的集合,是利用多棵树对样本进行训练并预测的一种分类器,其输出的类别是由个别树输出的类别的众数而定。随机森林结合了许多决策树,以降低过度拟合的风险。尽管有剪枝等等方法,一棵树的生成肯定还是不如多棵树,因此就有了随机森林,解决决策树泛化能力弱的缺点。随机森林运算量小,实现简单,常用于各种图像和数据的分类、水溶性预测、疾病诊断、人脸检测与关键点定位问题。该spark.ml实现支持使用连续和分类功能的随机林进行二进制和多类分类以及回归。
有关算法本身的更多信息,请参阅spark.mllib随机森林的文档。
我们在此列出输入和输出(预测)列类型。所有输出列都是可选的; 要排除输出列,请将其对应的Param设置为空字符串。
输入列(Input Columns)
| 参数名 |
类型 |
默认值 |
说明 |
| labelCol |
Double |
“标签” |
标签预测 |
| featuresCol |
Vector |
“特征” |
特征向量 |
输出列(Output Columns)
| 参数名 |
类型 |
默认 |
描述 |
备注 |
| predictionCol |
Double |
“预测” |
预测标签 |
|
| rawPredictionCol |
Vector |
“rawPrediction” |
向量长度#类别,具有进行预测的树节点处的训练实例标签的计数 |
仅限分类 |
| probabilityCol |
Vector |
“可能性” |
向量长度#类别等于rawPrediction归一化为多项分布 |
仅限分类 |
优点:
随机森林的既可以用于回归也可以用于分类任务,并且很容易查看模型的输入特征的相对重要性。随机森林算法被认为是一种非常方便且易于使用的算法,因为它是默认的超参数通常会产生一个很好的预测结果。超参数的数量也不是那么多,而且它们所代表的含义直观易懂。
随机森林有足够多的树,分类器就不会产生过度拟合模型。
缺点:
由于使用大量的树会使算法变得很慢,并且无法做到实时预测。一般而言,这些算法训练速度很快,预测十分缓慢。越准确的预测需要越多的树,这将导致模型越慢。在大多数现实世界的应用中,随机森林算法已经足够快,但肯定会遇到实时性要求很高的情况,那就只能首选其他方法。当然,随机森林是一种预测性建
模工具,而不是一种描述性工具。也就是说,如果你正在寻找关于数据中关系的描述,那建议首选其他方法。
适用范围:
随机森林算法可被用于很多不同的领域,如银行,股票市场,医药和电子商务。在银行领域,它通常被用来检测那些比普通人更高频率使用银行服务的客户,并及时偿还他们的债务。同时,它也会被用来检测那些想诈骗银行的客户。在金融领域,它可用于预测未来股票的趋势。在医疗保健领域,它可用于识别药品成分的正确组合,分析患者的病史以识别疾病。除此之外,在电子商务领域中,随机森林可以被用来确定客户是否真的喜欢某个产品。
随机森林构建:
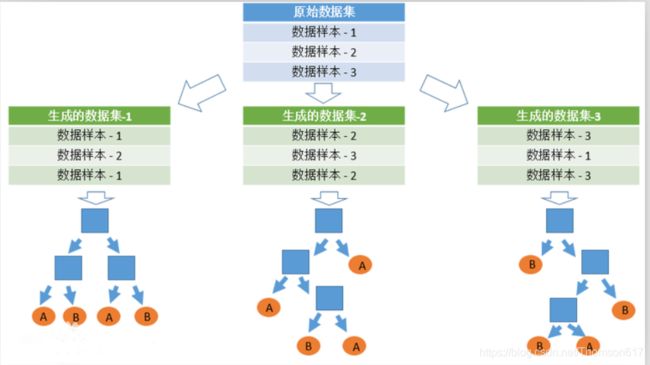
(1).数据的随机性选取:
首先,从原始的数据集中采取有放回的抽样,构造子数据集,子数据集的数据量是和原始数据集相同的。不同子数据集的元素可以重复,同一个子数据集中的元素也可以重复。第二,利用子数据集来构建子决策树,将这个数据放到每个子决策树中,每个子决策树输出一个结果。最后,如果有了新的数据需要通过随机森林得到分类结果,就可以通过对子决策树的判断结果的投票,得到随机森林的输出结果了。如下图,假设随机森林中有3棵子决策树,2棵子树的分类结果是A类,1棵子树的分类结果是B类,那么随机森林的分类结果就是A类。
(2).以及待选特征的随机选取:
与数据集的随机选取类似,随机森林中的子树的每一个分裂过程并未用到所有的待选特征,而是从所有的待选特征中随机选取一定的特征,之后再在随机选取的特征中选取最优的特征。这样能够使得随机森林中的决策树都能够彼此不同,提升系统的多样性,从而提升分类性能。
下图中,蓝色的方块代表所有可以被选择的特征,也就是目前的待选特征。黄色的方块是分裂特征。左边是一棵决策树的特征选取过程,通过在待选特征中选取最优的分裂特征(别忘了前文提到的ID3算法,C4.5算法,CART算法等等),完成分裂。右边是一个随机森林中的子树的特征选取过程。
梯度提升树(GBTs)
梯度提升树(Gradient-Boosted Trees,简称GBTs)是决策树的集合。GBT迭代训练决策树以最小化损失函数。该spark.ml实现支持使用连续和分类特征进行二进制分类和回归的GBT。更多信息请参阅spark.mllib有关GBT的文档。
我们在此列出输入和输出(预测)列类型。所有输出列都是可选的; 要排除输出列,请将其对应的Param设置为空字符串。
输入列(Input Columns)
| 参数名 |
类型 |
默认值 |
说明 |
| labelCol |
Double |
“标签” |
标签预测 |
| featuresCol |
Vector |
“特征” |
特征向量 |
输出列(Output Columns)
| 参数名 |
类型 |
默认 |
描述 |
备注 |
| predictionCol |
Double |
“预测” |
预测标签 |
|
在未来,GBTClassifier也会像RandomForestClassifier一样输出用于rawPrediction和probability的列。
7.聚类(Clustering)
聚类指事先并不知道任何样本的类别标号,希望通过某种算法来把一组未知类别的样本划分成若干类别,聚类的时候,我们并不关心某一类是什么,我们需要实现的目标只是把相似的东西聚到一起。聚类是一种无监督学习问题(即数据没有标注),该算法基于数据的内部结构寻找观察样本的自然族群(即集群),并且通常使用数据可视化评价结果。
聚类分析的目的就是让类群内观测的距离最近,同时不同群体之间的距离最大。通常用于探索性分析和作为分层监督学习管道的组成部分 (其中针对每个聚类训练不同的分类器或回归模型)。使用案例包括细分客户、新闻聚类、文章推荐等。
聚类算法主要是K-means,适用于无监督学习,适用的场景包括用户随机分群。分群后的数据更便于我们总结用户特征。LDA主要应用于文本类数据的分析,可以总结出各个文章群的主要主题,也就是各个分群的关注点。GMM和K-means比较类似,但是K-means中一个数据只属于一个簇,GMM会将一个数据分配到多个簇,并给出每个簇的概率。
在为基于RDD-API聚类指南还提供了有关这些算法的相关信息。
7.1聚类分析基本步骤:
1.数据预处理
(1).对数据进行标准化处理,处理异常值、补全缺失值,为了顺利应用聚类算法,还需要将用户画像中的所有标签以数值形式体现。
(2).对数值指标进行量纲缩放,使各指标具有相同的数量级,否则会使聚类结果产生偏差。
(3).要提取特征,把最初的特征集降维,从中选择有效特征放进聚类算法里跑.
我们可以通过关联规则分析(Association Rules)发现并排除高度相关的特征,也可以通过主成分分析(Principal Components Analysis,简称PCA)进行降维。
一般来说,聚类分析的数据都会进行标准化,标准化是因为聚类数据会受数据的量纲影响。
高维度/低维度:高维空间中的邻近度将趋向于0,导致各个点的临近度更加一致。维规约、因子分析、主成分分析。
数量级:数量级高的数据集,需要采用可伸缩性的算法。
稀疏性:
噪声、离群点:提前排除
数据属性:定量/分类,离散/连续
度量单位:将数据标准化,消除属性单位的影响
权重:对属性进行加权
2.确定维度
用户分类是分析在这些维度上的用户是否有显著的区别,因此聚类分析的数据维度的选择是至关重要的。
需要考虑两个方面:
目标:首先,维度的选择在大方向上是要与需要解决的问题相一致。即用户在这些维度上有显著的区别。换句话说,这些维度需要能够表明用户的特征,以助于产品设计或优化。如:用户行为特征,来针对不同用户做不同的设计;活跃度等特征,找出高价值用户;
维度的特征:对于单个维度,数据的分布以正态分布为佳,其他分布应该进行数据处理。长尾分布可以取log10()。对于多个维度,维度应该不具有很强的相关性。有很强的相关性,可以作因子分析。
另外,CLIQUE算法,可以发现子空间的簇,来筛选合适的维度。
3.确定聚类个数
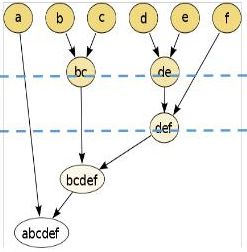
层次聚类是十分常用的聚类算法,是根据每两个对象之间的距离,将距离最近的对象两两合并,合并后产生的新对象再进行两两合并,以此类推,直到所有对象合为一类。
Ward方法在实际应用中分类效果较好,应用较广。它主要基于方差分析思想,理想情况下,同类对象之间的离差平方和尽可能小,不同类对象之间的离差平方和应该尽可能大。该方法要求样品间的距离必须是欧氏距离。
值得注意的是,在R中,调用ward方法的名称已经从“ward”更新为“ward.D”。
根据R绘制的层次聚类图像,我们对该企业的客户相似性有一个直观了解,然而单凭肉眼,仍然难以判断具体的聚类个数。这时我们通过轮廓系数法进一步确定聚类个数。
轮廓系数旨在对某个对象与同类对象的相似度和与不同类对象的相似度做对比。轮廓系数取值在-1到1之间,轮廓系数越大时,表示对应簇的数量下,聚类效果越好。在轮廓系数的实际应用中,不能单纯取轮廓系数最大的K值,还需要考虑聚类结果的分布情况(避免出现超大群体),以及从商业角度是否易于理解与执行,据此综合分析,探索合理的K值。
4.选择合适的聚类方法
(1).基于原型的聚类 Prototype-Based Clustering
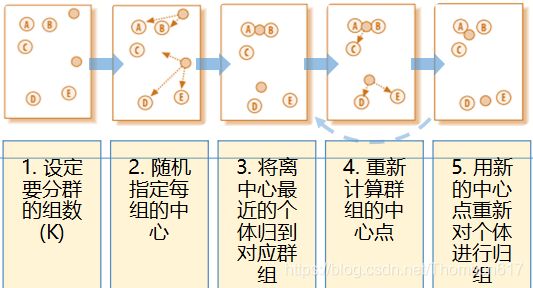
K-means是基于距离的聚类算法,十分经典,简单而高效。其主要思想是选择K个点作为初始聚类中心, 将每个对象分配到最近的中心形成K个簇,重新计算每个簇的中心,重复以上迭代步骤,直到簇不再变化或达到指定迭代次数为止。K-means算法缺省使用欧氏距离来计算。
Mixture Models 混合模型:EM算法
优点:比k均值或模糊c均值更一般,可以使用各种类型的分布
缺点:EM算法可能很慢;不能很好处理近似协线型的数据点;在正确的模型形式方面也存在问题。
Self-Organizing Maps(SOM)自组织映射。
(2).基于密度的聚类 Density-Based Clustering
DBSCAN.
Subspace Clustering子空间聚类.
CLIQUE(Clustering In quest)系统地发现子空间簇的基于网格的聚类算法.
(3).基于图的聚类 Graph-Based Clustering
Sparsification稀疏化:断开相似度小于一定阈值的边,或仅保留连接到点的k个最近邻的边。
Minimum Spanning Tree(MST) Clustering最小生成树聚类:产生与单链凝聚聚类相同的聚类。
Chameleon:Hierarchical Clustering with Dynamic Modeling:稀疏化、图划分、层次凝聚。
Jarvis-Patrick聚类算法:以SNN相似度取代两个点之间的邻近度。
(4).可伸缩的聚类算法 Scalable Clustering Algorithm
BIRCH(Balanced Iterative Reducing and Clustering using Hierarchies):能够处理离群点。是一种增量的聚类方法,因为它对每一个数据点的聚类的决策都是基于当前已经处理过的数据点,而不是基于全局的数据点。主要是在数据体量很大的时候使用,而且数据类型是numerical。
CURE(Clustering Using REpresentative):处理离群点和具有非球形和非均匀大小的簇的数据。在簇里选定一定数量的点,彼此最远,以代表簇的形状。
5.聚类结果分析与展示
将可合并的结果进行合并,并针对客户群体制订运营策略。
7.2聚类算法的种类:
基于网格的聚类算法:
| STING |
利用网格单元保存数据统计信息,从而实现多分辨率的聚类 |
| WaveC1uster |
在聚类分析中引入了小波变换的原理,主要应用于信号处理领域。(备注:小波算法在信号处理,图形图象,加密解密等领域有重要应用,是一种比较高深和牛逼的东西) |
| CLIQUE |
是一种结合了网格和密度的聚类算法 |
| OPTIGRID |
|
基于划分(质心)的聚类算法(partition clustering):
| k-means |
是一种典型的划分聚类算法,它用一个聚类的中心来代表一个簇,即在代过程中选择的聚点不一定是聚类中的一个点,该算法只能处理数值型数据 |
| k-modes |
K-Means算法的扩展,采用简单匹配方法来度量分类型数据的相似度 |
| k-prototypes |
结合了K-Means和K-Modes两种算法,能够处理混合型数据 |
| k-medoids |
在迭代过程中选择簇中的某点作为聚点,PAM是典型的k-medoids-算法 |
| CLARA |
CLARA算法在PAM的基础上采用了抽样技术,能够处理大规模数据 |
| CLARANS |
CLARANS算法融合了PM和CLARA两者的优点,是第一个用于空间数据库的聚类算法 |
| Focused CLARAN |
采用了空间索引技术提高了CLARANS算法的效率 |
| PCM |
模糊集合理论引入聚类分析中并提出了PCM模糊聚类算法 |
基于层次(连通性)的聚类算法:
| CURE |
采用抽样技术先对数据集D随机抽取样本,再采用分区技术对样本进行分区,然后对每个分区局部聚类,最后对局部聚类进行全局聚类 |
| ROCK |
也采用了随机抽样技术,该算法在计算两个对象的相似度时,同时考虑了周围对象的影响 |
| CHEMALOEN (变色龙算法) |
首先由数据集构造成一个K-最近邻图Gk,再通过一个图的划分算法将图ck划分成大量的子图,每个子图代表一个初始子簇,最后用一个凝聚的层次聚类算法反复合并子簇,找到真正的结果簇 |
| SBAC |
SBAC算法则在计算对象间相似度时,考虑了属性特征对于体现对象本质的重要程度,对于更能体现对象本质的属性赋子较高的权值 |
| BIRCH |
BIRCH算法利用树结构对数据集进行处理,叶结点存储一个聚类,用中心和半径表示,顺序处理每一个对象,并把它划分到距离最近的结点,该算法也可以作为其他聚类算法的预处理过程 |
| BUBBLE |
BUBBLE算法则把BIRCH算法的中心和半径概念推广到普通的距离空间 |
| BUBBLE-FM |
BUBBLE-FM算法通过减少距离的计算次数,提高了BUBBLE算法的效率 |
基于密度的聚类算法:
| DBSCAN |
DBSCAN算法是一种典型的基于密度的聚类算法,该算法采用空间素引技术来搜索对象的邻城,引入了“核心对象”和“密度可达”等概念,从核心对象出发,把所有密度可达的对象组成一个簇 |
| GDBSCAN |
算法通过泛化DBSCAN算法中邻域的概,以适应空间对象的特点 |
| OPTICS |
OPTICS算法结合了聚类的自动性和交互性,先生成聚类的次序,可以对不同的聚类设置不同的参数,来得到用户满意的结果 |
| FDC |
FDC算法通过构造k-d tree把整个数据空间划分成若干个矩形空间,当空间维数较少时可以大大提高DBSCAN的效率 |
基于神经网络的聚类算法:
| 自组织神经网络SOM |
该方法的基本思想是:由外界输入不同的样本到人工的自组织映射网络中,一开始时,输入样本引起输出兴奋细胞的位置各不相同,但自组织后会形成一些细胞群,它们分别代表了输入样本,反映了输入样本的特征 |
基于统计学的聚类算法:
| COBWeb |
COBWeb是一个通用的概念聚类方法,它用分类树的形式表现层次聚类 |
| CLASSIT |
|
| AutoClass |
是以概率混合模型为基础,利用属性的概率分布来描述聚类,该方法能够处理混合型的数据,但要求各属性相互独立 |
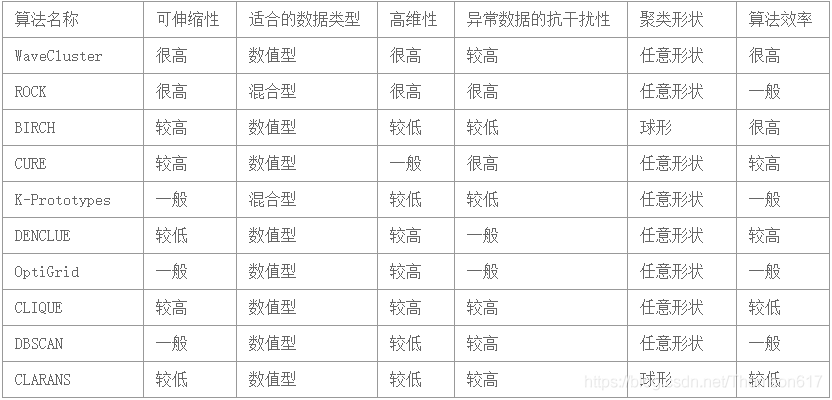
几种常用的聚类算法从可伸缩性、适合的数据类型、高维性(处理高维数据的能力)、异常数据的抗干扰度、聚类形状和算法效率6个方面进行了综合性能评价,评价结果如下表所示:
7.3 K均值聚类(K-means)
k-means是最常用的聚类算法之一,它将数据点聚类成预定义数量的聚类。聚类的度量基于样本点之间的几何距离(即在坐标平面中的距离)。集群是围绕在聚类中心的族群,而集群呈现出类球状并具有相似的大小。MLlib实现包括一个名为kmeans ||的k-means ++方法的并行变体。
Kmeans算法分析步骤:
1.确定聚类个数K .
2.选定K个D维向量作为初始类中心 .
3.对每个样本计算与聚类中心的距离,选择最近的作为该样本所属的类 .
4.在同一类内部,重新计算聚类中心(几何重心),不断迭代,直到收敛:![]() (损失函数为此就是Kmeans算法(其实是默认了我们样布服从均值为μ,方差为某固定值的K个高斯分布,混合高斯分布),如果(x-μ)不是平方,而只是绝对值那就是Kmedian算法,混合拉普拉斯分布)每个样本到聚类中心的距离之和或平方和不再有很大变化。对损失函数求导,,可以看到其实我们更新聚类中心的时候,就是按照梯度的方向更新的。由于损失函数有局部极小值点,所以它是初值敏感的,取不同的初值可能落在不同的极小值点。
(损失函数为此就是Kmeans算法(其实是默认了我们样布服从均值为μ,方差为某固定值的K个高斯分布,混合高斯分布),如果(x-μ)不是平方,而只是绝对值那就是Kmedian算法,混合拉普拉斯分布)每个样本到聚类中心的距离之和或平方和不再有很大变化。对损失函数求导,,可以看到其实我们更新聚类中心的时候,就是按照梯度的方向更新的。由于损失函数有局部极小值点,所以它是初值敏感的,取不同的初值可能落在不同的极小值点。
优点:速度快,适合发现球形聚类,可发现离群点.
缺点:1.对初始聚类中心敏感,缓解方案是多初始化几遍,选取损失函数小的。 2.必须提前指定K值(指定的不好可能得到局部最优解),缓解方法,多选取几个K值,grid search选取几个指标评价效果情况。 3.属于硬聚类,每个样本点只能属于一类 。 4.对异常值免疫能力差,可通过一些调整(取均值最近的样本点,非均值点)。 5.对团状数据点区分度好,对于带状不好(谱聚类或特征映射)。尽管它有这么多缺点,但是它仍然应用广泛,因为它速度快,并且可以并行化处理。
缺失值问题:离散的特征:将缺失的作为单独一类,90%缺失去掉。连续的特征:其他变量对这个变量回归,做填补;样本平均值填补;中位数填补。
对于初始点选择的问题,有升级的算法Kmeans++,每次选取新的中心点时,有权重的选取(权重为距离上个中心点的距离),
cls = KMeans(n_clusters=4, init='k-means++',random_state=0)不给出随机种子,每次聚类结果会不一样。另外,想要收敛速度进一步加快,可以使用Mini-BatchKmeans,也就是求梯度的时候用的是随机梯度下降的方法,而不是批量梯度下降。
参数说明:
| 参数 |
含义 |
默认值 |
| K |
聚类数目 |
2 |
| maxIter |
最大迭代次数 |
20 |
| seed |
集群初始化时的随机种子.种子不同,产生不同的随机数 |
None |
| initMode |
初始化模式 |
k-means|| |
| tol |
迭代算法的收敛性参数 |
1e-4 |
| initSteps |
初始化步数,用于KMeans|| |
5 |
| 每一个参数均可通过名为setXXX(...)(如maxIter即为setMaxIter() |
||
KMeans实现为a Estimator并生成一个KMeansModel基本模型。
|
|
参数名 |
类型 |
默认 |
描述 |
| 输入列 |
featuresCol |
Vector |
“特征” |
特征向量 |
| 输出列 |
predictionCol |
Int |
“预测” |
预测的集群中心 |
例子:
Scala代码:
import org.apache.spark.ml.clustering.KMeans
import org.apache.spark.ml.evaluation.ClusteringEvaluator
// 加载数据
val dataFrame = spark.read.format("libsvm").load("/sample_kmeans_data.txt")
val Array(trainingData, testData) = dataFrame.randomSplit(Array(0.8, 0.2))
// 设置K值及最大迭代次数.seed 表示集群初始化时的随机种子。种子不同,产生不同的随机数。种子相同,即使实例不同也产生相同的随机数。
val kmeans = new KMeans().setK(2).setSeed(1L).setMaxIter(50)
val model = kmeans.fit(trainingData)
// 作出预测
val predictions = model.transform(testData)
Predictions.show()
// predictions.filter("prediction='2'").show(30)
/**
集合内误差平方和(Within Set Sum of Squared Error, WSSSE) 用来度量聚类的有效性.通过 WSSSE 的计算构建出 K-WSSSE 间的相关关系,从而确定K的值,一般来说,最优的K值即是 K-WSSSE 曲线的 拐点(Elbow) 位置(当然,对于某些情况来说,我们还需要考虑K值的语义可解释性,而不仅仅是教条地参考WSSSE曲线)
*/
val WSSSE : Double = model.computeCost(trainingData)
// 通过计算轮廓线评分来评估聚类(一般来说越大越好)(但要避免出现超大群体)
val evaluator = new ClusteringEvaluator()
val silhouette = evaluator.evaluate(predictions)
println(s"Silhouette with squared euclidean distance = $silhouette")
// 显示结果.
println("Cluster Centers: ")
model.clusterCenters.foreach(println)Java代码:
import org.apache.spark.ml.clustering.KMeansModel;
import org.apache.spark.ml.clustering.KMeans;
import org.apache.spark.ml.evaluation.ClusteringEvaluator;
import org.apache.spark.ml.linalg.Vector;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
Dataset dataset = spark.read().format("libsvm").load("/sample_kmeans_data.txt");
KMeans kmeans = new KMeans().setK(2).setSeed(1L);
KMeansModel model = kmeans.fit(dataset);
Dataset predictions = model.transform(dataset);
ClusteringEvaluator evaluator = new ClusteringEvaluator();
double silhouette = evaluator.evaluate(predictions);
System.out.println("Silhouette with squared euclidean distance = " + silhouette);
Vector[] centers = model.clusterCenters();
System.out.println("Cluster Centers: ");
for (Vector center: centers) {
System.out.println(center);
}
7.4文档主题模型(LDA)
LDA(Latent dirichlet allocation,隐含狄利克雷分配)是一种三层贝叶斯主题模型,通过无监督的学习方法发现文本中隐含的主题信息,目的是要以无指导学习的方法从文本中发现隐含的语义维度-即“Topic”或者“Concept”。隐性语义分析的实质是要利用文本中词项(term)的共现特征来发现文本的Topic结构,这种方法不需要任何关于文本的背景知识。
LDA被实现为一个支持EMLDAOptimizer和OnlineLDAOptimizer的Estimator,并生成一个LDAModel作为基本模型。如果需要,专家用户可以将EMLDAOptimizer生成的LDAModel强制转换为DistributedLDAModel。
LDA可以用来识别大规模文档集(document collection)或语料库(corpus)中潜藏的主题信息。它采用了词袋(bag of words)的方法,这种方法将每一篇文档视为一个词频向量,从而将文本信息转化为了易于建模的数字信息。但是词袋方法没有考虑词与词之间的顺序,这简化了问题的复杂性,同时也为模型的改进提供了契机。每一篇文档代表了一些主题所构成的一个概率分布,而每一个主题又代表了很多单词所构成的一个概率分布。
LDA可以被认为是如下的一个聚类过程:
(1)各个主题对应于各类的“质心”,每一篇文档被视为数据集中的一个样本。
(2)主题和文档都被认为存在一个向量空间中,这个向量空间中的每个特征向量都是词频(词袋模型)。
(3)与采用传统聚类方法中采用距离公式来衡量不同的是,LDA使用一个基于统计模型的方程,而这个统计模型揭示出这些文档都是怎么产生的。
例子:
Scala代码:
import org.apache.spark.ml.clustering.LDA
val dataset = spark.read.format("libsvm").load("/sample_lda_libsvm_data.txt")
// Trains a LDA model.
val lda = new LDA()
.setK(10) //主题数量(聚簇中心数量)
.setMaxIter(10) //最大迭代次数
.setDocConcentration(1.1) //文档在主题上分布的先验参数(超参数α).当前必须大于1,值越大,推断出的分布越平滑。默认为-1,自动设置.
.setTopicConcentration(1.1) //主题在单词上的先验分布参数。当前必须大于1,值越大,推断出的分布越平滑。默认为-1,自动设置.
.setCheckpointInterval(10) //检查点间隔。maxIterations很大的时候,检查点可以帮助减少shuffle文件大小并且可以帮助故障恢复.
.setOptimizer("em") //优化计算方法,目前支持"em", "online"
val model = lda.fit(dataset)
val ll = model.logLikelihood(dataset)
val lp = model.logPerplexity(dataset)
println(s"整个语料库的日志可能性的下界: $ll")
println(s"复杂度的上限: $lp")
// Describe topics.
val topics = model.describeTopics(3)
println("The topics described by their top-weighted terms:")
topics.show(false)
// Shows the result.
val transformed = model.transform(dataset)
transformed.show(false)Java代码:
import org.apache.spark.ml.clustering.LDA;
import org.apache.spark.ml.clustering.LDAModel;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;
Dataset dataset = spark.read().format("libsvm").load("/sample_lda_libsvm_data.txt");
LDA lda = new LDA().setK(10).setMaxIter(10);
LDAModel model = lda.fit(dataset);
double ll = model.logLikelihood(dataset);
double lp = model.logPerplexity(dataset);
System.out.println("The lower bound on the log likelihood of the entire corpus: " + ll);
System.out.println("The upper bound on perplexity: " + lp);
Dataset topics = model.describeTopics(3);
System.out.println("The topics described by their top-weighted terms:");
topics.show(false);
Dataset transformed = model.transform(dataset);
transformed.show(false);
7.5 二分K-均值算法(Bisecting k-Means)
二分k-means(Bisecting k-means)是一种使用分裂(或“自上而下”)方法的层次聚类:所有观察都在一个聚类中开始,并且当一个向下移动层次结构时,递归地执行拆分。
二分KMeans(Bisecting KMeans)算法的主要思想是:首先将所有点作为一个簇,然后将该簇一分为二。之后选择能最大限度降低聚类代价函数(也就是误差平方和)的簇划分为两个簇。以此进行下去,直到簇的数目等于用户给定的数目k为止。以上隐含的一个原则就是:因为聚类的误差平方和能够衡量聚类性能,该值越小表示数据点越接近于他们的质心,聚类效果就越好。所以我们就需要对误差平方和最大的簇进行再一次划分,因为误差平方和越大,表示该簇聚类效果越不好,越有可能是多个簇被当成了一个簇,所以我们首先需要对这个簇进行划分。
平分K-means通常比常规K-means快得多,但它通常会产生不同的聚类。
BisectingKMeans实现为Estimator并生成一个BisectingKMeansModel基本模型。
例子:
Scala代码:
import org.apache.spark.ml.clustering.BisectingKMeans
val dataset = spark.read.format("libsvm").load("/kmeans_data.txt")
// Trains a bisecting k-means model.
val bkm = new BisectingKMeans().setK(2).setSeed(1)
val model = bkm.fit(dataset)
// Evaluate clustering.
val cost = model.computeCost(dataset)
println(s"Within Set Sum of Squared Errors = $cost")
// Shows the result.
println("Cluster Centers: ")
val centers = model.clusterCenters
centers.foreach(println)Java代码:
import org.apache.spark.ml.clustering.BisectingKMeans;
import org.apache.spark.ml.clustering.BisectingKMeansModel;
import org.apache.spark.ml.linalg.Vector;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
Dataset dataset = spark.read().format("libsvm").load("/kmeans_data.txt");
BisectingKMeans bkm = new BisectingKMeans().setK(2).setSeed(1);
BisectingKMeansModel model = bkm.fit(dataset);
double cost = model.computeCost(dataset);
System.out.println("Within Set Sum of Squared Errors = " + cost);
System.out.println("Cluster Centers: ");
Vector[] centers = model.clusterCenters();
for (Vector center : centers) {
System.out.println(center);
}
7.6高斯混合模型(GMM)
高斯混合模型(Gaussian Mixture Model) 表示一个复合分布,从k个高斯子分布中抽取点,每个子分布都有自己的概率。属于判别模型。该spark.ml实现使用 期望最大化 来诱导给定一组样本的最大似然模型。
GaussianMixture实现为a Estimator并生成一个GaussianMixtureModel基本模型。
|
|
参数名 |
类型 |
默认 |
描述 |
| 输入列 |
featuresCol |
Vector |
“特征” |
特征向量 |
| 输出列 |
predictionCol |
Int |
“预测” |
预测的集群中心 |
| predictionCol |
Vector |
“可能性/概率” |
每个集群的概率 |
例子:
Scala代码:
import org.apache.spark.ml.clustering.GaussianMixture
val dataset = spark.read.format("libsvm").load("/kmeans_data.txt")
// Trains Gaussian Mixture Model
val gmm = new GaussianMixture().setK(2)
val model = gmm.fit(dataset)
// 混合模型的输出参数
for (i <- 0 until model.getK) {
println(s"Gaussian $i:\nweight=${model.weights(i)}\n" + s"mu=${model.gaussians(i).mean}\nsigma=\n${model.gaussians(i).cov}\n")
}Java代码:
import org.apache.spark.ml.clustering.GaussianMixture;
import org.apache.spark.ml.clustering.GaussianMixtureModel;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
Dataset dataset = spark.read().format("libsvm").load("/kmeans_data.txt");
GaussianMixture gmm = new GaussianMixture().setK(2);
GaussianMixtureModel model = gmm.fit(dataset);
for (int i = 0; i < model.getK(); i++) {
System.out.printf("Gaussian %d:\nweight=%f\nmu=%s\nsigma=\n%s\n\n", i, model.weights()[i], model.gaussians()[i].mean(), model.gaussians()[i].cov());
}
7.7层次聚类(Hierarchical / Agglomerative)
层次聚类也称系统聚类法,是根据个体间距离将个体向上两两聚合,再将聚合的小群体两两聚合一直到聚为一个整体。计算所有个体之间的距离,最相近距离的个体合体,不断合体。
层次聚类是一系列基于以下概念的聚类算法:
最开始由一个数据点作为一个集群;
对于每个集群,基于相同的标准合并集群;
重复这一过程直到只留下一个集群,因此就得到了集群的层次结构。优点:层次聚类最主要的优点是集群不再需要假设为类球形。另外其也可以扩展到大数据集。
缺点:有点像 K 均值聚类,该算法需要设定集群的数量(即在算法完成后需要保留的层次)。