AdaBoost算法原理及python实现(手动感叹号)
目录
- 什么是AdaBoost
- 算法流程
- python实现
什么是AdaBoost
AdaBoost是Boosting算法的一种,比较出名,它可以将多个弱分类器线性组合成一个强分类器,通俗的说就是“三个臭皮匠,顶个诸葛亮”。其要求弱分类器好而不同,每个分类器的准确率要在50%以上。
算法流程
AdaBoos先初始化样本权值分布,并从初始训练集训练出一个基学习器,再根据这个基学习器的分类结果对训练样本的权值分布进行调整,再生成新的基学习器,依次进行下去,直到满足要求。其流程如下:
(1)初始化样本权值分布
(2)生成基本分类器G1
(3)计算分类器系数 α \alpha α
(4)更新训练数据的权值分布
(5)生成新的分类器G2
(6)循环(2-5)
(7)将所有的分类器线性相加。
这个过程看起来比较难理解,同时书上公式太多,看得头大,所以咱们还是举个简单的例子吧,这个例子是李航《统计学习方法》里的。假设我们有这样一些数据:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
x x x表示样本值, y y y是这些样本的标签,我们现在要做的就是根据x的值建立一个模型来预测y的值。本质上是一个二分类问题,建立一个分类器将这些样本进行分类,1表示正例,-1表示反例。在正式开始之前,我们先假定这些样本的权值 w w w都是一样的,都为0.1(总共10个样本,权值的和为1),如下表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| w1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
权值初始化代码如下:
def func_w_1(x):
w_1=[]
for i in range(len(x)):
w_1.append(0.1)
return w_1
假设我们最初的分类器可以将前n个样本识别为正例,剩下的样本为反例,可以用下面的公式表达: G i ( x ) = { 1 xu (1) Gi(x)= \begin{cases} 1& \text{x
其中 u u u为阈值, i i i是下标(不会编辑,哭了),为了方便讨论我们将u的值设置为:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| u | -0.5 | 0.5 | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
阈值生成的代码如下:
def func_threshs(x):
threshs =[i-0.5 for i in x]
threshs.append(x[len(x)-1]+0.5)
return threshs
对于每一个分类器 G i ( x ) Gi(x) Gi(x),其误差率 e e e可用其出错(即 G i ( x i ) ≠ y i Gi(xi)\neq yi Gi(xi)=yi)的权值和来表示,比如当阈值为2.5时,该分类器为 G i ( x ) = { 1 x<2.5 − 1 x>2.5 (2) Gi(x)= \begin{cases} 1& \text{x<2.5}\\ -1& \text{x>2.5} \end{cases}\tag{2} Gi(x)={1−1x<2.5x>2.5(2)
或者
G i ( x ) = { − 1 x<2.5 1 x>2.5 (3) Gi(x)= \begin{cases} -1& \text{x<2.5}\\ 1& \text{x>2.5} \end{cases}\tag{3} Gi(x)={−11x<2.5x>2.5(3)
这样每一个阈值都可以生成2种分类器,因此共有22个分类器。对于分类器 ( 2 ) (2) (2)给定输入 x x x,其输出 G G G如下
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
| G | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
分类器实现的代码如下:
def func_cut(threshs):
y_pres_all={}#定义正向分类器,形如公式2
y_last_all={}#定义正向分类器,形如公式3
for thresh in threshs:
y_pres=[]
y_last=[]
for i in range(len(x)):
if x[i]<thresh:
y_pres.append(1)
y_last.append(-1)
else:
y_pres.append(-1)
y_last.append(1)
y_pres_all[thresh]=y_pres
y_last_all[thresh]=y_last
return y_pres_all,y_last_all
从表中可以看出,样本7、8、9分错了,故其误差率e=w7+w8+w9=0.3。我们用同样的方法求这22个分类器的误差率,选择误差率最小的作为基分类器。计算误差率的代码如下:
def sub_func_e(y,w_n,y_pres_all,thresh):
e=0
for i in range(len(y)):
if y_pres_all[thresh][i]!=y[i]:
e+=w_n[i];
return e
def sub_func_e_s(y,w_n,y_pres_all,threshs):
e_s={}
e_min=1
n=0
for thresh in threshs:
e=sub_func_e(y,w_n,y_pres_all,thresh)
e_s[thresh]=round(e,6)
if e<e_min:
e_min=round(e,6)
n=thresh
return e_s,e_min,n
def sub_func_e_all(y,w_n,y_pres_all,y_last_all,threshs):
e_s1,e_min1,n1=sub_func_e_s(y,w_n,y_pres_all,threshs)
e_s2,e_min2,n2=sub_func_e_s(y,w_n,y_last_all,threshs)
if e_min1<=e_min2:
return e_s1,e_min1,n1,y_pres_all
else:
return e_s2,e_min2,n2,y_last_all
在我们的例子中,通过计算所有的误差率得到基分类器为公式2所示。下面开始计算分类器的系数 α \alpha α,其计算公式如下:
α = 1 2 l n 1 − e e (4) \alpha=\frac{1}{2}ln\frac{1-e}{e}\tag{4} α=21lne1−e(4) 由此可见误差率e不能大于0.5,否则会使得 α \alpha α<0。本例中 α = 1 2 l n 1 − 0.3 0.3 = 0.4236 \alpha=\frac{1}{2}ln\frac{1-0.3}{0.3}=0.4236 α=21ln0.31−0.3=0.4236,计算分类器系数的代码如下:
def func_a_n(e_min):
a_n=round(0.5*math.log((1-e_min)/e_min),6)
return a_n
最后再根据以上计算的结果更新权值分布w2,更新的公式如下:
w 2 i = w 1 ( i ) Z ∗ e − α i ∗ y i ∗ G 1 ( x i ) (5) w2i=\frac{w1(i)}{Z}*e^{-\alpha{i}*yi*G1(xi)}\tag{5} w2i=Zw1(i)∗e−αi∗yi∗G1(xi)(5)其中 Z = ∑ i = 1 m w 1 ( i ) ∗ e − α i ∗ y i ∗ G 1 ( x i ) (6) Z=\sum_{i=1}^m w1(i)*e^{-\alpha{i}*yi*G1(xi)}\tag{6} Z=i=1∑mw1(i)∗e−αi∗yi∗G1(xi)(6)
m是样本的个数,不难看出 Z Z Z的作用是让新生成的样本权值的和为1,通过该公式计算可以得到新的权值分布:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| w2 | 0.07143 | 0.07143 | 0.07143 | 0.07143 | 0.07143 | 0.07143 | 0.16667 | 0.16667 | 0.16667 | 0.07143 |
举个例子,第一个样本的权值更新成了0.07143,这个是怎么来的呢,是这样算的: w 1 ( 1 ) Z ∗ e − α 1 ∗ y 1 ∗ G 1 ( x 1 ) = 0.1 5.50011 ∗ e − 0.4236 ∗ 1 ∗ 1 = 0.07143 , 其 中 Z = 0.07143 ∗ 7 + 0.16667 ∗ 3 = 5.50011 \frac{w1(1)}{Z}*e^{-\alpha{1}*y1*G1(x1)}=\frac{0.1}{5.50011}*e^{-0.4236*1*1}=0.07143,其中Z=0.07143*7+0.16667*3=5.50011 Zw1(1)∗e−α1∗y1∗G1(x1)=5.500110.1∗e−0.4236∗1∗1=0.07143,其中Z=0.07143∗7+0.16667∗3=5.50011,其实就是w2的和。从表里可以看出,之前分错的样本7,8,9的权值提高了,其余的则下降了。样本分布权值的更新代码如下:
def func_w_n_tmp(x,pre_n,w_n,a_n):
w_n_tmp=[]
for i in range(len(x)):
w_new=round(w_n[i]*math.exp(-1*a_n*y[i]*pre_n[i]),6)
w_n_tmp.append(w_new)
return w_n_tmp
def func_z_n(w_n_tmp):
z_n=sum(w_n_tmp)
return z_n
def func_w_n(w_n_tmp,z_n):
w_n=[round(i/z_n,5) for i in w_n_tmp]
return w_n
我们用同样的流程可以得到多个分类器及多个分类器权值分布,共同组成了新的分类器,即
G ( X ) = s i g n [ f ( x ) ] G(X)=sign[f(x)] G(X)=sign[f(x)]其中
f ( x ) = α 1 ∗ G 1 ( x ) + α 2 ∗ G 2 ( x ) + ⋅ ⋅ ⋅ α n ∗ G n ( x ) f(x)=\alpha1*G1(x)+\alpha2*G2(x)+\cdot\cdot\cdot\alpha n*Gn(x) f(x)=α1∗G1(x)+α2∗G2(x)+⋅⋅⋅αn∗Gn(x)
s i g n [ f ( x ) ] sign[f(x)] sign[f(x)]表示当 f ( x ) f(x) f(x)大于0时取1,小于0时取-1,书上给出的3个分类器的集成,结果为 f ( x ) = 0.4236 ∗ G 1 ( x ) + 0.6496 ∗ G 2 ( x ) + 0.7514 ∗ G 3 ( x ) f(x)=0.4236*G1(x)+0.6496*G2(x)+0.7514*G3(x) f(x)=0.4236∗G1(x)+0.6496∗G2(x)+0.7514∗G3(x),其中: G 1 ( x ) = { 1 x<2.5 − 1 x>2.5 G1(x)= \begin{cases} 1& \text{x<2.5}\\ -1& \text{x>2.5} \end{cases} G1(x)={1−1x<2.5x>2.5 G 2 ( x ) = { 1 x<8.5 − 1 x>8.5 G2(x)= \begin{cases} 1& \text{x<8.5}\\ -1& \text{x>8.5} \end{cases} G2(x)={1−1x<8.5x>8.5 G 3 ( x ) = { − 1 x<5.5 1 x>5.5 G3(x)= \begin{cases} -1& \text{x<5.5}\\ 1& \text{x>5.5} \end{cases} G3(x)={−11x<5.5x>5.5
则 f ( x ) f(x) f(x)为 f ( x ) = { 0.4236 + 0.6496 − 0.7514 = 0.3218 x<2.5 − 0.4236 + 0.6496 − 0.7514 = − 0.5254 2.5
最终的分类器
G ( x ) = { 1 x<2.5 − 1 2.5
模型的输出如下:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
| G | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
正确率为100%!是不是很神奇?
python实现
最后我们用python实现上述例子中的结果,我们像书上那样,设置3个分类器,具体的实现代码如下:
#导入相关的库
import math
import pandas as pd
import numpy as np
#输入原始数据
x=[0,1,2,3,4,5,6,7,8,9]
y=[1,1,1,-1,-1,-1,1,1,1,-1]
T=3 #设置分类器个数
#初始化样本权值分布函数
def func_w_1(x):
w_1=[]
for i in range(len(x)):
w_1.append(0.1)
return w_1
#生成阈值函数
def func_threshs(x):
threshs =[i-0.5 for i in x]
threshs.append(x[len(x)-1]+0.5)
return threshs
#根据阈值生成22种分类器的输出
def func_cut(threshs):
y_pres_all={}
y_last_all={}
for thresh in threshs:
y_pres=[]
y_last=[]
for i in range(len(x)):
if x[i]<thresh:
y_pres.append(1)
y_last.append(-1)
else:
y_pres.append(-1)
y_last.append(1)
y_pres_all[thresh]=y_pres #前向分类器
y_last_all[thresh]=y_last #后向分类器
return y_pres_all,y_last_all
#求一个分类器误差率e
def sub_func_e(y,w_n,y_pres_all,thresh):
e=0
for i in range(len(y)):
if y_pres_all[thresh][i]!=y[i]:
e+=w_n[i];
return e
#求一类分类器误差率
def sub_func_e_s(y,w_n,y_pres_all,threshs):
e_s={}
e_min=1
n=0
for thresh in threshs:
e=sub_func_e(y,w_n,y_pres_all,thresh)
e_s[thresh]=round(e,6)
if e{'x':x,'y':y,'w_1':w_n_s[0],'pre_1':pre_n_s[0],'g_1':g_n_s[0],
'w_2':w_n_s[1],'pre_2':pre_n_s[1],'g_2':g_n_s[1],
'w_3':w_n_s[2],'pre_3':pre_n_s[2],'g_3':g_n_s[2]}
df=pd.DataFrame(data)
df['sum']=df['g_1']+df['g_2']+df['g_3']
#输出预测值
df['G(x)']=np.sign(df['sum'])
df.T
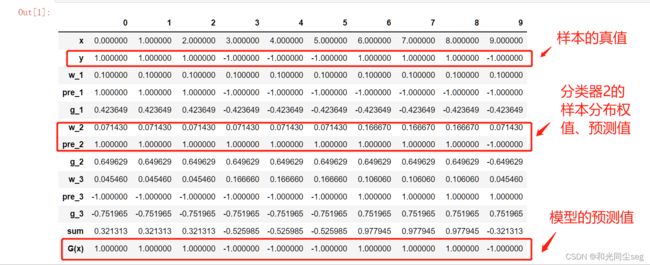
程序的输出结果如下:
备注:以上代码参考b站up主“致敬大神”,大家都去点波关注啊,哈哈哈,溜了溜了,有问题可以留言。