机器学习：Adaboost算法(原理+python实现）

Adaboost算法

一 算法的实质

对于指定的分类器G(x),其分类效果可能未必理想，那么Adaboot算法则通过将分类器进行线性组合来提升分类效果,其表达式如下：

其中，x为数据的特征，f(x)为数据对应的分类类别，a_m为加权权重。G_m (x)为分类器函数G(x)第m次训练时数据所对应的分类类别，a_m为第m次训练时所对应的加权权重。

二 算法的实现

输入：针对一个训练集
其中x_i表示第i个数据的特征，y_i表示第i个数据的分类类别，其中分类类别有1和-1。

输出：分类器函数f(x)

步骤：(1) 对于n个数据，其每个数据都配有一个权重系数，因此组成一个权重分布D，其初始值为

可以看出数据的总权重为1，初始状态下每个样本的权重都是一样的。
(2) 针对于训练集T，训练出最佳分类器G_m (x)，由于训练目标属于分类类型，因此以分类误差率最小时所对应的分类器为最佳分类器，其分类误差率计算如下：

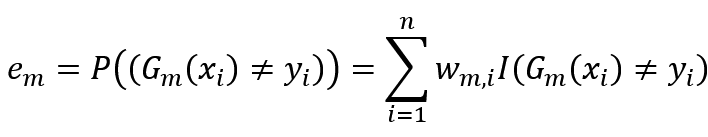
可以看出，分类误差率等于样本分类错误时所对应权重系数之和。
(3) 计算G_m (x)所对应的a_m

(4) 更新训练集的权重分布

经步骤(1),循环(2)-(4)步骤，就可以迭代训练出G_1 (x)，G_2 (x)…G_m (x)，因此通过以下公式即可计算出令人满意的分类效果。

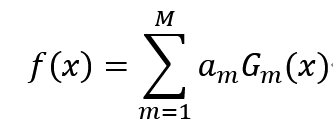
三 代码的实现逻辑

应用情景：
训练集
其中x_i表示第i个数据的特征，y_i表示第i个数据的分类类别，其中分类类别有1和-1，这一次利用单层决策树构建G(x)来完成Adaboost算法。
根据应用需求，我们的代码实现逻辑具体如下：

在每一次构造训练器时：
	在指定权重分布D下训练出最佳的单层决策树
	将最佳的单层决策树加入单层决策树集合
	计算alpha
	更新权重分布D
	如果分类错误率为0，则退出循环
返回单层决策树集合

在上述环节中，比较关键的是如何在指定权重分布D下训练出最佳的单层决策树，对此的代码实现逻辑如下：

	对于数据集每一个特征：
		对于数据集每一个特征值：
			对于不等号的方向：
				建立一个单层决策树
				如果错误率低于minerro，则该单层决策树为最佳决策树
	返回最佳单层决策树

四 代码实例
1.加载数据集

def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if data[i,-1] == 0:
            data[i,-1] = -1
    # print(data)
    return data[:,:2], data[:,-1]
# 执行算法
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)

2.构建Adaboost

class AdaBoost:
    def __init__(self, n_estimators=50, learning_rate=1.0):
        self.clf_num = n_estimators   # 分类器的个数
        self.learning_rate = learning_rate   # 移动步伐
    def init_args(self, datasets, labels):
        self.X = datasets  # 样本数据
        self.Y = labels  # 样本分类类别
        self.M, self.N = datasets.shape   # 样本的个数和特征数
        self.clf_sets = []  # 弱分类器数目和集合
        self.weights = [1.0 / self.M] * self.M    # 初始化weights
        self.alpha = []  # G(x)系数 alpha
    # 选的哪个特征后，找出最佳特征值
    def _G(self, features, labels, weights):
        m = len(features)
        error = 100000.0
        best_v = 0.0
        # 单维features
        features_min = min(features)
        features_max = max(features)
        n_step = (features_max - features_min +
                  self.learning_rate) // self.learning_rate
        direct, compare_array = None, None
        for i in range(1, int(n_step)):
            v = features_min + self.learning_rate * i
            if v not in features:
                compare_array_positive = np.array(
                    [1 if features[k] > v else -1 for k in range(m)])
                weight_error_positive = sum([
                    weights[k] for k in range(m)
                    if compare_array_positive[k] != labels[k]
                ])

                compare_array_nagetive = np.array(
                    [-1 if features[k] > v else 1 for k in range(m)])
                weight_error_nagetive = sum([
                    weights[k] for k in range(m)
                    if compare_array_nagetive[k] != labels[k]
                ])

                if weight_error_positive < weight_error_nagetive:
                    weight_error = weight_error_positive
                    _compare_array = compare_array_positive
                    direct = 'positive'
                else:
                    weight_error = weight_error_nagetive
                    _compare_array = compare_array_nagetive
                    direct = 'nagetive'
                # print('v:{} error:{}'.format(v, weight_error))
                if weight_error < error:
                    error = weight_error
                    compare_array = _compare_array
                    best_v = v
        return best_v, direct, error, compare_array

    # 计算alpha
    def _alpha(self, error):
        return 0.5 * np.log((1 - error) / error)

    # 规范化因子
    def _Z(self, weights, a, clf):
        return sum([
            weights[i] * np.exp(-1 * a * self.Y[i] * clf[i])
            for i in range(self.M)
        ])
    # 权值更新
    def _w(self, a, clf, Z):
        for i in range(self.M):
            self.weights[i] = self.weights[i] * np.exp(
                -1 * a * self.Y[i] * clf[i]) / Z

    # G(x)的线性组合
    def _f(self, alpha, clf_sets):
        pass
    def G(self, x, v, direct):
        if direct == 'positive':
            return 1 if x > v else -1
        else:
            return -1 if x > v else 1
    def fit(self, X, y):
        self.init_args(X, y)
        for epoch in range(self.clf_num):
            best_clf_error, best_v, clf_result = 100000, None, None
            # 在众多特征中，选出误差最小的特征
            for j in range(self.N):
                features = self.X[:, j]
                # 分类阈值，分类误差，分类结果
                v, direct, error, compare_array = self._G(features, self.Y, self.weights)
                if error < best_clf_error:
                    best_clf_error = error      # 分类误差
                    best_v = v                  # 分类特征值
                    final_direct = direct       # 判断是大于特征值为1 还是小于特征值为1
                    clf_result = compare_array  # 分类结果
                    axis = j                    # 特征索引
                if best_clf_error == 0:         # 如果误差为0，就直接选择该特征和特征值
                    break
            # 计算G(x)系数a
            a = self._alpha(best_clf_error)
            self.alpha.append(a)
            # 记录分类器
            self.clf_sets.append((axis, best_v, final_direct))
            Z = self._Z(self.weights, a, clf_result)
            # 权值更新
            self._w(a, clf_result, Z)

    def predict(self, feature):
        result = 0.0
        for i in range(len(self.clf_sets)):
            axis, clf_v, direct = self.clf_sets[i]
            f_input = feature[axis]
            result += self.alpha[i] * self.G(f_input, clf_v, direct)
        return 1 if result > 0 else -1

    def score(self, X_test, y_test):
        right_count = 0
        for i in range(len(X_test)):
            feature = X_test[i]
            if self.predict(feature) == y_test[i]:
                right_count += 1
        return right_count / len(X_test)

3.进行测试

clf = AdaBoost(n_estimators=10, learning_rate=0.2)  # 10个分类器
clf.fit(X_train, y_train)
print(clf.score(X_test, y_test))

因为数据集每次划分的训练和测试集不同，所以每次运行的结果会有所不同，我运行第三次划分的数据集的预测效果较好，如下所示：