有营养的算法笔记（六)

喧闹和富有

1.对应letecode链接
喧闹和富有

2.题目描述

3.解题思路

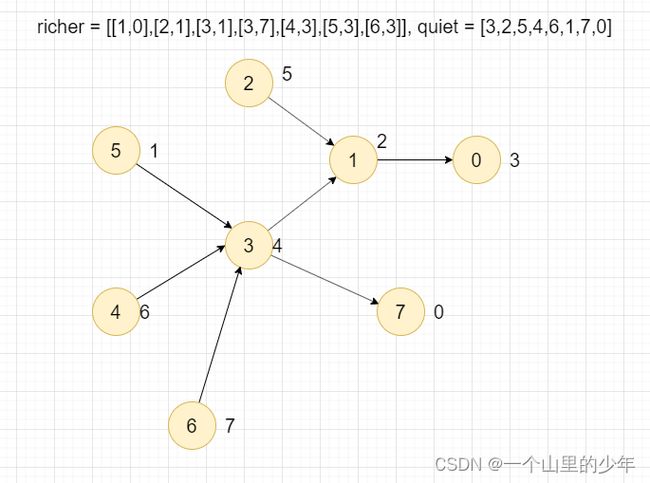
这是一个典型的拓扑排序的题目[a,b]代表a比b更有钱那么也就意味着a到b有一条有向边。大概的思路就是我们先生成邻接表，和每个节点的入度是多少，定义一个队列把入度为0的节点加入到队列当中，然后遍历整个这个节点所有的邻居节点去除这个点对其邻居节点影响。如果此时比这个点大的且安静的值比其邻居节点的安静值要小则更新邻居节点的安静值。一直这么传递下去即可。下面我们来举个列子：

首先先生成好邻居表，然后将入度为0的节点加入到队列当中，一开始我们认为比自己大且安静值最小的是自己。首先我们将2，5，4，6加入到队列当中，首先弹出一个2然后消除它对其邻居节点影响，但是此时5的安静值比1的安静值要大不更新，然后弹出5消除对其邻居节点的影响，但是此时5的安静值要比3要小此时我们更新3的安静值为1，一次这样操作之后既可得到答案。

4.对应代码

class Solution {
public:
    vector<int> loudAndRich(vector<vector<int>>& richer, vector<int>& quiet) {
                int N=quiet.size();
                vector<vector<int>>nexts(N);
                //邻居节点
                vector<int>degree(N);
                //记录入度
               for(auto&node:richer)
               {
                     nexts[node[0]].push_back(node[1]);
                     ++degree[node[1]];
               }
               
               queue<int>zeroQueue;
               for(int i=0;i<N;i++)
               {
                   if(degree[i]==0){
                       zeroQueue.push(i);
                   }
               }
               vector<int>ans(N);
               for(int i=0;i<N;i++){
                   ans[i]=i;
                   //一开始认为自己比自己更有钱且安静值最小
               }
               while(!zeroQueue.empty())
               {
                       auto node=zeroQueue.front();
                       zeroQueue.pop();
                       
                       for(auto next:nexts[node])
                       {
                           //往下传递即更新
                           if(quiet[ans[node]]<quiet[ans[next]]){
                               ans[next]=ans[node];
                               
                           }
                            
                            if(--degree[next]==0){
                                zeroQueue.push(next);
                            }
                       }
               }
               return ans;

    }
};

完成任务的天数

1.本题为某家公司的笔试题再这里没有这个测试链接，再这里只给出解题思路和代码

2.题目描述

来自hulu
有n个人，m个任务，任务之间有依赖记录在int[][] depends里
比如: depends[i] = [a, b]，表示a任务依赖b任务的完成
其中 0 <= a < m，0 <= b < m
1个人1天可以完成1个任务，每个人都会选当前能做任务里，标号最小的任务
一个任务所依赖的任务都完成了，该任务才能开始做
返回n个人做完m个任务，需要几天

3.解题思路

本题依然是拓扑排序，只不过本题我们需要维护一个工人队列，这个入度为0的队列不在是这个普通的队列，而是整个优先级队列。还是上题的那个思路，我们首先生成邻接表将入度为0的节点加入到队列当中，此时我们需要维护一个数组用来记录每个任务最早什么时候才可以开工，因为一个任务要等到它的入度为0的时候才能被做。我们在减少一个点对其邻居节点的影响时需要更新它能被做的时间。

4.对应代码

#include
#include
#include
#include
using namespace std;
 //来自hulu
 //有n个人，m个任务，任务之间有依赖记录在int[][] depends里
 //比如: depends[i] = [a, b]，表示a任务依赖b任务的完成
 //其中 0 <= a < m，0 <= b < m
 //1个人1天可以完成1个任务，每个人都会选当前能做任务里，标号最小的任务
 //一个任务所依赖的任务都完成了，该任务才能开始做
 //返回n个人做完m个任务，需要几天
class Soulution
{
public:
	int Days(vector<vector<int>>& depends, int n,int m)
	{
		vector<vector<int>>nexts;
		vector<int>degree;
		GetNexts(depends, nexts, degree, m);
		//生成邻接表和入度表
		priority_queue<int, vector<int>, greater<int>>works;
		//小根堆用来维护这个工人记录它什么时候能够醒来
		for (int i = 0; i < n; i++) {
			works.push(0);
		}
		priority_queue<int, vector<int>, greater<int>>zeroQueue;
		//入度表
		for (int i = 0; i < m; i++)
		{
		//入度为0的点加入到队列当中来
			if (degree[i] == 0) {
			
				zeroQueue.push(i);
			}
		}

		vector<int>start(m);
		int finishAll = 0;
		int done = 0;
		while (!zeroQueue.empty())
		{
			int job = zeroQueue.top();
			zeroQueue.pop();
			++done;
			int wake = works.top();
			works.pop();
			//整个任务什么时候能做和工人醒来的时间两者取最大值才是完成这个时间
			int finish = max(start[job], wake)+1;
			//完成他需要一天时间
			finishAll = max(finishAll, finish);
			for (auto next : nexts[job])
			{
				start[next] = max(start[next], finish);
				if (--degree[next] == 0) {//入度为0了可以进队列了
					zeroQueue.push(next);
				}
			}
			works.push(finish);
		}
		//开任务是否都做完了
		return done == m ? finishAll : -1;
	}
	//生成邻接表
	void GetNexts(vector<vector<int>>& depends,vector<vector<int>>&next,vector<int>&degree,int m)
	{
		int N = depends.size();
		next.resize(m);
		degree.resize(m);
		for (auto& depend : depends)
		{
			next[depend[1]].push_back(depend[0]);
			++degree[depend[0]];
		}

	}
	
};
int main1()
{
	// 2 -> 5 -> 6
		//           |
		//           v
		// 1 -> 4 -> 7
		//      ^
		//      |
		// 0 -> 3
	vector<vector<int>>arr{
				{ 3, 0 },
				{ 4, 1 },
				{ 5, 2 },
				{ 4, 3 },
				{ 6, 5 },
				{ 7, 4 },
				{ 7, 6 }
	};
	cout << Soulution().Days(arr, 3, 8) << endl;
	cout << Soulution().Days(arr, 8, 8) << endl;
	
	return 0;

}

需要的面试官数量

1.同样的本题是公司的笔试题，没有这个测试连接在这里给出解题思路和这个代码。
2.题目描述

给定义二维数组其中[a,b]代表的含义为a代表起始时间,b代表的是会议的结束时间。面试的开始时间和结束时间不可以改变。每个面试官最多面试m场超过m场就不可以在面试了。请你返回需要多少个面试官

3.解题思路

这个题了非常的简单我们只需要将会议的开始时间进行排序，一开始放入一个面试官记录它那个时刻才能继续进行面试，和面试了几个人放入到优先级队列当中。优先级队列按照这个醒来的时间进行排序。遍历排好序的会议数组然后再弹出一个面试官比较这个他醒来的时间和你这个会议的开始时间来决定要不要增加面试官即可

4.对应代码

#include
#include
#include
#include
using namespace std;
class Solution
{
public:
	int needManger(vector<vector<int>>& meetings,int limit)
	{
		if (limit == 1) {
			return meetings.size();
		}
		typedef pair<int, int>pa;
		sort(meetings.begin(), meetings.end(), [&](vector<int>& a, vector<int>& b) {return a[0] < b[0]; });
		//先按照每一场会议的开始时间进行排序
		auto cmp = [&](pair<int, int>& a, pair<int, int>& b) {return a.first > b.first; };

		priority_queue<pa, vector<pa>, decltype(cmp)>minHeap(cmp);
		int all = 1;
		minHeap.push({0,0});
		//小根堆
		for (auto meeting : meetings)
		{
			if (minHeap.empty() || minHeap.top().first > meeting[1]) {
				all++;
				minHeap.push({ meeting[1],1 });
			 }
			else
			{
				auto mannger = minHeap.top();
				minHeap.pop();
				//如果已经达到上限了不用再放回到队列当中
				if (mannger.second < limit - 1) {
					mannger.second++;
					mannger.first = meeting[1];
					minHeap.push(mannger);
				}
			
			}
		}


		return all;

	}

};
int main()
{
	vector<vector<int>>arr{ {3,17},{4,13},{5,6},{6,27} };
	cout << Solution().needManger(arr,3) << endl;
	return 0;
}