【leetcode刷题】数组篇

二分查找

力扣链接：二分查找

给定一个 n 个元素有序的（升序）整型数组nums和一个目标值 target ，写一个函数搜索nums中的 target，如果目标值存在返回下标，否则返回 -1。

这里我们看到它数组里面的元素是不重复的，所以可以用二分查找。

二分查找的第一种写法：左闭右闭[]

假如题目如下：

int left=0;//找到左值
int right=numsSize-1;//找到右值
int middle=0;
while(left<=right)
{
    middle=(left+right)/2;//找到中间值
    if(nums[middle]>target)//如果要找的值在middle的左边，则更新右边去寻找区间[left,middle-1]
    {
right=middle-1;
    }
    else if(nums[middle]<target)//如果要找的值在middle的右边则更新左边去寻找区间[middle+1,right]
    {
left=middle+1;
    }
    else//middle就是target
    {
        return middle;
    }
}
 //没找到
 return -1;

二分查找的第二种写法：左闭右开[)

假如题目如下：

int left=0;//找到左值
int right=numsSize;//找到右值
int middle=0;
while(left<right)
{
    middle=(left+right)/2;//找到中间值
    if(nums[middle]>target)//如果要找的值在middle的左边，则更新右边去寻找区间[left,middle]
    {
right=middle;
    }
    else if(nums[middle]<target)//如果要找的值在middle的右边则更新左边去寻找区间[middle+1,right]
    {
left=middle+1;
    }
    else//middle就是target
    {
        return middle;
    }
}
 //没找到
 return -1;

移除元素

力扣链接：移除数组

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。

双指针法

要知道数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。

int fast=0;
int slow=0;
for(;fast<numsSize;fast++)
{
    if(nums[fast]!=val)//当元素不为val时，prev才会往前走一步，cur把prev覆盖；所以最后prev的位置就为不是val元素的个数
    {
        nums[slow++]=nums[fast];
    }
}
return slow;

有序数组的平方

力扣链接：有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

一开始我想的是按照上个题目（移除数组）双指针的方法，遇到元素平方就好拉…但是元素里面可能有负数，所以这样行不同。我们就换个思路，既然负数的平方也是正数，那么只用比大小就好了。于是乎就有了下列思路：

既然都是平方，那么本身顺序也是负数->0->整数从小到大排列，则有可能最左边的负数平方后可能比最右边的正数的平方还要大！

那么平方后的顺序则为：越靠近两边的数的平方越大，排列后位置越靠后；越靠近中间的数的平方越小，排列后为之前越靠前；但我们很难判断最小的数从前往后排序了，所以咱们可以试试判断最大的数从后往前排序！！！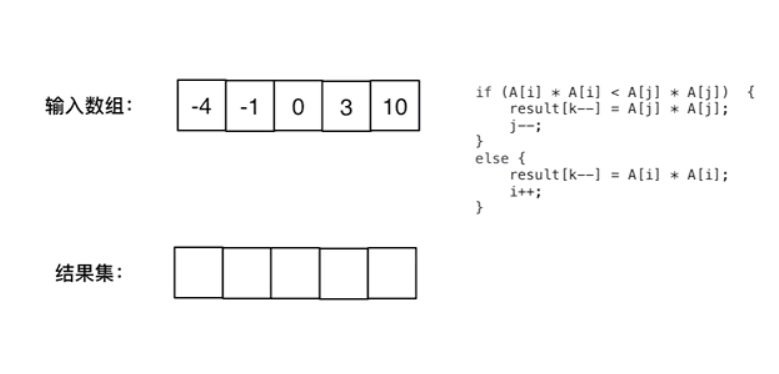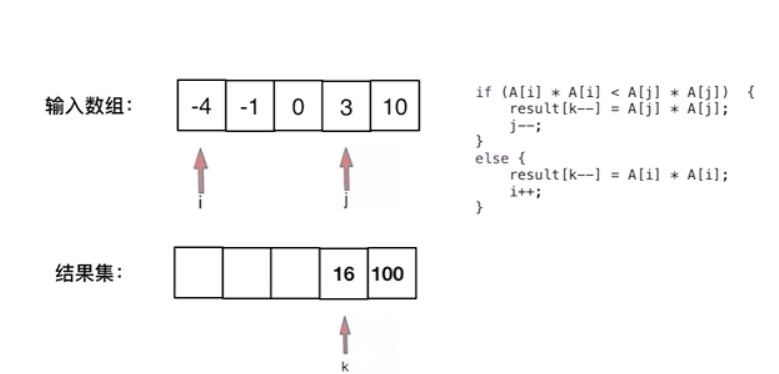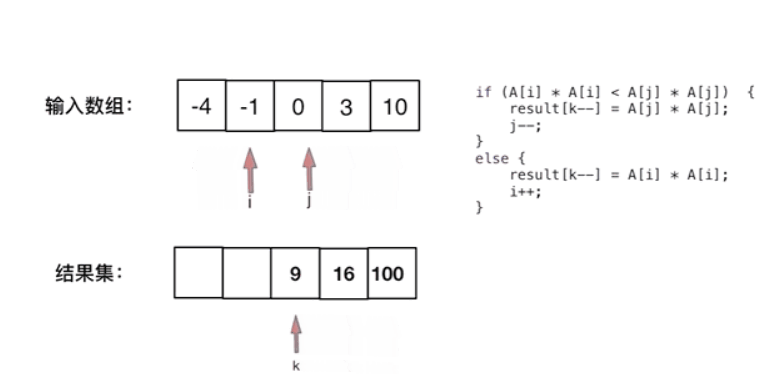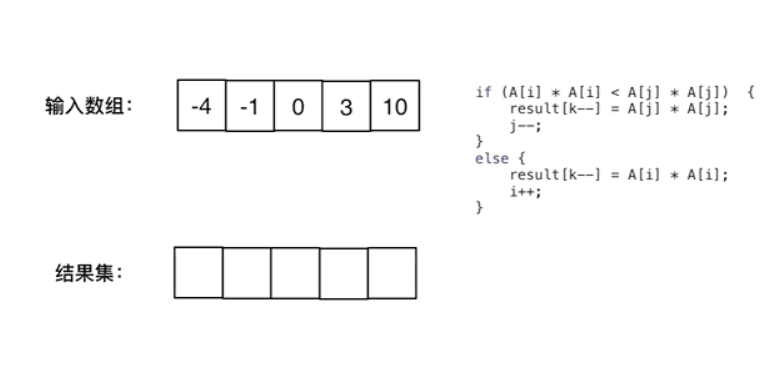

int* sortedSquares(int* nums, int numsSize, int* returnSize){
*returnSize=numsSize;
int index=numsSize-1;
int left=0;//左边
int right=numsSize-1;//右边
int*ans=(int*)malloc(sizeof(int)*numsSize);//开空间用来装平方
for(;index>=0;index--)
{
    //先寄存平方
int leftsquare=nums[left]*nums[left];
int rightsquare=nums[right]*nums[right];
    //把最大的数放最后-从后往前按从大到小排列
if(leftsquare>rightsquare) //左边的大就放最后
{
    ans[index]=leftsquare;
    left++;
}
else//右边的比左边的大或相等放最后
{
    ans[index]=rightsquare;
    right--;
}
}
return ans;
}

长度最小的子数组

力扣链接：长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target ；找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

int minSubArrayLen(int target, int* nums, int numsSize){
int slow=0;
int fast=0;
int minlength=INT_MAX;//最小数组长
int sum=0;
for(;fast<numsSize;++fast)
{
    sum+=nums[fast];//窗口内的数加起来
    while(sum>=target) //当窗口内总数加起来比target大时
    {
        int longlength=fast-slow+1;
        minlength=minlength<longlength?minlength :longlength;
        sum-=nums[slow++];//逐个删除窗口最左边的数直到窗口内数总和小于target
    }

}
return minlength==INT_MAX?0:minlength;//如果最小长度没变，说明不符合条件
}

螺旋矩阵

力扣链接：螺旋矩阵

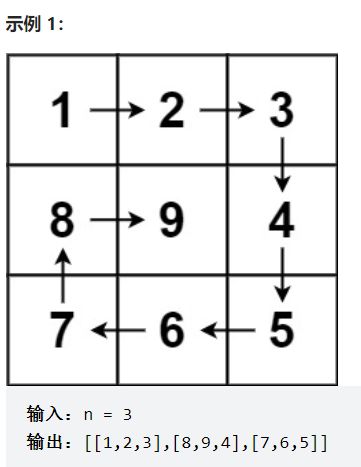
给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

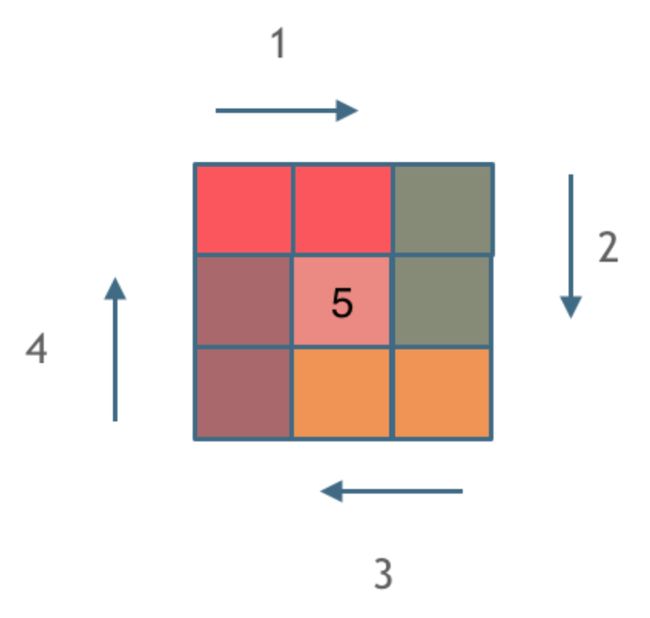
在这题我们要严格按照循环不变量原理（在这里☞在四条边循环时判定边界时的条件要一样）

模拟顺时针画矩阵的过程:

• 填充上行从左到右

• 填充右列从上到下

• 填充下行从右到左

• 填充左列从下到上

  

当n为单数时必定会剩出中间一个元素在螺旋循环时没有循环到，这里我们要另外讨论

int** generateMatrix(int n, int* returnSize, int** returnColumnSizes){
*returnSize=n;
*returnColumnSizes=(int*)malloc(sizeof(int)*n);//开辟好n*n的空间
int** ans=(int**)malloc(sizeof(int*)*n);//这里开辟大小为n的ans
int i;
for(int i=0;i<n;i++)
{
    ans[i]=(int*)malloc(sizeof(int)*n);
    //这里在数量为n的ans空间上再开辟n个空间->总数也是n*n
    (*returnColumnSizes)[i]=n;//初始化
}
//开始循环按照[x,n-1][y,y-1]思路排序
int startx=0;
int starty=0;
int offset=1;//偏移量
int loop=n/2;//圈数
int middle=n/2;//中间数
int count=1;//从1到n^2的计数
while(loop)
{
    int x=startx;
    int y=starty;
    //从左往右
    for(;x<n+startx-offset;x++)
    {
        ans[starty][x]=count++;
    }
    //从上往下
    for(;y<n+starty-offset;y++)
    {
        ans[y][x]=count++;
    }
    //从右往左
    for(;x>startx;x--)
    {
        ans[y][x]=count++;
    }
    //从下往上
    for(;y>starty;y--)
    {
        ans[y][x]=count++;
    }
    startx++;//x的起始位+1
    starty++;//y的起始位+1
    offset+=2;//偏移位+2！
    loop--;//圈数-1
}
if(n%2)//这里是n%2看有没有余数！不是middle%2
{
    ans[middle][middle]=count;//中间数另外算
}
return ans;
}

总结

以上内容是我看[代码随想录]并做题后的感想和思路，如果对你有帮助的话不妨给个小小的~~~

代码随想录链接：代码随想录

最后最后，祝大家国庆节快乐呀！！！