机器学习之逻辑回归
一、逻辑回归基本介绍
Logistic Regression
- 用于分类问题
- 监督学习算法
二、逻辑回归工作原理
根据现有数据对分类边界线建立回归公式 ,具体分为以下三步
1. 将决策边界表示为
z = W1X1+W2X2+···+WnXn + b (W0X0)
2. 把决策边界函数经过Sigmoid函数运算得到概率:
- 概率大于0.5分类为1
- 概率小于0.5分类为0
3.使损失函数最小化来获得最佳的参数向量θ
如果分类为1,则概率越小表示分类错误程度越高;如果分类为0,则概率越大表示分类错误程度越高。经过推导,最后用梯度下降法计算损失函数最小值。
三、python实现逻辑回归
import random
import numpy as np
import matplotlib.pyplot as plt
def loadDataSet():
dataMat = []
labelMat = []
f = open("testSet.txt")
for line in f.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
f.close()
return dataMat, labelMat
def sigmoid(inX):
return 1.0/(1+np.exp(-inX))
"""
这里的损失函数简单使用:
1-p if y=1
p if y=0
损失函数=|正确值y - 预测值p|
符合如果y=1 p越小,cost越大, 如果y=0,p越大,cost越大
"""
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) # 转换成np的mat格式
labelMatrix = np.mat(classLabels).transpose() # 转换成np的mat格式并进行转置
m, n = np.shape(dataMatrix)
alpha = 0.001 # 学习率
maxCycles = 500 # 最大迭代次数
weights = np.ones((n, 1)) # 创建一个n行1列的数组,每个回归系数初始化为1,loadDataSet()已经将X0设为1; WX = w0(X0=1) + w1X1 + w2X2
for k in range(maxCycles):
h = sigmoid(dataMatrix*weights)
error = (labelMatrix - h) # 对函数关于回归系数求导后得到参数更新的表达式:w = w +α(h-y)x
weights = weights + alpha*dataMatrix.transpose()*error # 定性地说,此处计算真实类别与预测类别的差值,接下来就是按照该差值的方向调整回归系数
return weights.getA() # 将矩阵转换为数组,和np.mat()相反
# 区别:1. 变量h和误差error都是数值,但在梯度下降里面是向量;
# 2. 没有矩阵转换过程,所有变量数据类型都是numpy数组
def stocGradAscent(dataMatrix, classLabels, numIter=150):
m, n = np.shape(dataMatrix) # 返回dataMatrix的大小。m为行数,n为列数。
weights = np.ones(n) # 参数初始化
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4/(1.0+j+i)+0.01 # 降低alpha的大小,每次减小1/(j+i)。
randIndex = int(random.uniform(0,len(dataIndex))) # 随机选取样本
h = sigmoid(sum(dataMatrix[dataIndex[randIndex]]*weights)) # 选择随机选取的一个样本,计算h
error = classLabels[dataIndex[randIndex]] - h # 计算误差
weights = weights + alpha * error * dataMatrix[dataIndex[randIndex]] # 更新回归系数
del(dataIndex[randIndex]) # 删除已经使用的样本
return weights
def plotBestFit(weights):
dataMat, labelMat = loadDataSet() # 加载数据集
dataArr = np.array(dataMat) # 转换成numpy的array数组
n = np.shape(dataMat)[0] # 数据个数
xcord1 = []; ycord1 = [] # 正样本
xcord2 = []; ycord2 = [] # 负样本
for i in range(n): # 根据数据集标签进行分类
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1]); ycord1.append(dataArr[i, 2]) # 1为正样本
else:
xcord2.append(dataArr[i, 1]); ycord2.append(dataArr[i, 2]) # 0为负样本
fig = plt.figure()
ax = fig.add_subplot(111) # 添加subplot
ax.scatter(xcord1, ycord1, s=20, c='red', marker='s', alpha=.5) # 绘制正样本
ax.scatter(xcord2, ycord2, s=20, c='green', alpha=.5) # 绘制负样本
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.title('BestFit') # 绘制title
plt.xlabel('X1'); plt.ylabel('X2') # 绘制label
plt.show()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet()
weights = stocGradAscent(np.array(dataMat), labelMat)
plotBestFit(weights)
四、sklearn实现逻辑回归
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666) # 设置固定的随机数种子
X = np.random.normal(0, 1, size=(200, 2)) # 均值为0,方差为1的随机数样本
y = np.array(X[:, 0]**2 + X[:, 1] < 1.5, dtype='int') # 强制使一个Boolean类型转为int型,True则取1,False则取0
for _ in range(20): # 添加噪音
y[np.random.randint(200)] = 1 # 随机挑20个点,强制让分类结果为1
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()
from sklearn.model_selection import train_test_split # 分割数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
# 导入LogisticRegression
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
print(log_reg.score(X_train, y_train))
print(log_reg.score(X_test, y_test)) # 分数并不高,因为样本数据是二次函数型的
# 绘制决策边界
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
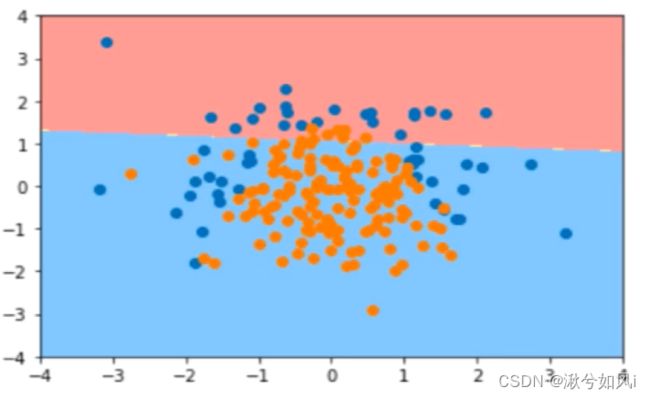
plot_decision_boundary(log_reg, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
LogisticRegression() 构造函数的参数及默认值
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False)
penalty:默认为’l2’,默认正则化方式为l2正则化,还有l1正则化。C:默认是1.0,正则化参数max_iter:算法收敛最大迭代次数,int类型,默认为10
sklearn中对逻辑回归进行多项式回归、正则化等
# 多项式回归
def PolynomialLogisticRegression(degree, C, penalty='l2'):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scaler', StandardScaler()),
('log_reg', LogisticRegression(C=C, penalty=penalty))
])
poly_log_reg4 = PolynomialLogisticRegression(degree=20, C=0.1, penalty='l1')
poly_log_reg4.fit(X_train, y_train)
poly_log_reg4.score(X_train, y_train)
poly_log_reg4.score(X_test, y_test)
实现多项式回归等具体内容参考bobo老师课程
五、决策边界的绘制
线性拟合时,我们可以通过画出决策边界线,边界上边的是一类,边界下面的是一类。但当决策边界不规则时,即不是简单的直线时,就很难用这种方法绘制出决策边界线。新的思路是:每次来一个点,判断它分为“蓝色”还是“红色”的类,对平面中足够密的点都进行判断和绘制,最后就能显现出决策边界。

# 绘制决策边界
def plot_decision_boundary(model, axis): # axis是坐标轴的范围
# 将x轴和y轴划分为无数的小点
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()] # 连接x0,x1 进行ravel扁平化
y_predict = model.predict(X_new) # 对于所有的点,都用model进行预测
zz = y_predict.reshape(x0.shape) # 扁平化后形状变了
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
#-----------------------------------------------------------------------------------#
plot_decision_boundary(log_reg, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
总结
优缺点
1. 优点
- 训练速度较快,可解释性高
2. 缺点
- 容易欠拟合,精度不高
问题
- 待完善