机器学习｜（I）机器学习概述

第一章 机器学习概述

1. 机器学习

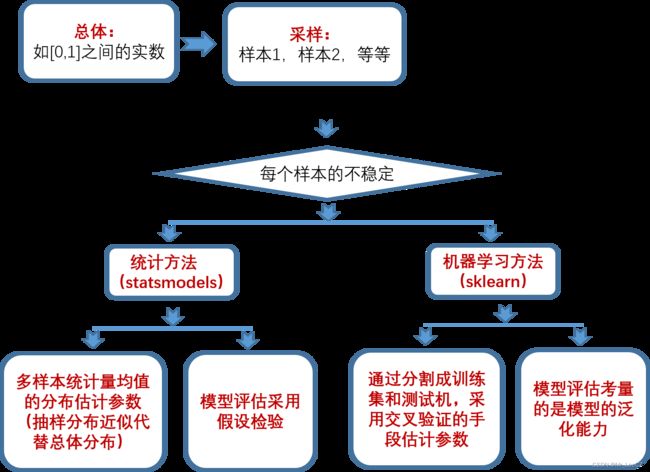
机器学习是一门多学科交叉专业，涵盖概率论知识，统计学知识，近似理论知识和复杂算法知识，使用计算机作为工具并致力于真实实时的模拟人类学习方式，并将现有内容进行知识结构划分来有效提高学习效率。

2. 机器学习基础

2.1 数据的表达

矩阵或者向量来源于线性方程组的求解
$$\mathbf{Ax}=\mathbf{b}\text{\hspace{1em}(1)}$$
其中，$\mathbf{A}\in {\mathbb{R}}^{n\times m}$​ 称为矩阵，$\mathbf{x}\in {\mathbb{R}}^m$​ 和 $\mathbf{b}\in {\mathbb{R}}^n$​ 称为向量。式(1)中矩阵可看作列向量的堆砌$\mathbf{A}=[{\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_m]=\left[\begin{array}{c}{\mathbf{w}}_1^{\top }\\ {\mathbf{w}}_2^{\top }\\ ⋮\\ {\mathbf{w}}_n^{\top }\end{array}\right]$​，$\mathbf{x}=[x_1,x_2,\cdots ,x_m{]}^{\top }$​，$\mathbf{b}=[b_1,b_2,\cdots ,b_n{]}^{\top }$​。可从不同的视角认识式(1)

• 矩阵的线性算子

  矩阵 $\mathbf{A}$​ 可看作是一个线性算子，包括对向量 $\mathbf{x}$​ 的平移、旋转或者伸缩三种线性作用，这种线性运算在数学表达式上是加权求和的形式，即式(1)可表示为

$$\mathbf{Ax}=\left[\begin{array}{c}{\mathbf{w}}_1^{\top }\\ {\mathbf{w}}_2^{\top }\\ ⋮\\ {\mathbf{w}}_n^{\top }\end{array}\right]\cdot \mathbf{x}=\left[\begin{array}{c}{\mathbf{w}}_1^{\top }\mathbf{x}\\ {\mathbf{w}}_2^{\top }\mathbf{x}\\ ⋮\\ {\mathbf{w}}_n^{\top }\mathbf{x}\end{array}\right]=\left[\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_n\end{array}\right]\text{\hspace{1em}(2)}$$

即
$$\left[\begin{array}{c}{\mathbf{w}}_1^{\top }\mathbf{x}=b_1\\ {\mathbf{w}}_2^{\top }\mathbf{x}=b_2\\ ⋮\\ {\mathbf{w}}_n^{\top }\mathbf{x}=b_n\end{array}\right]$$

• 矩阵列表达

$$\mathbf{Ax}=[{\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_m]\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_m\end{array}\right]=x_1{\mathbf{a}}_1+x_2{\mathbf{a}}_2+\cdots +x_m{\mathbf{a}}_m=\mathbf{b}$$

2.2 内积与投影

定义：$⟨\mathbf{x},\mathbf{y}⟩={\mathbf{x}}^{\top }\mathbf{y}={\mathbf{y}}^{\top }\mathbf{x}={\sum }_{i=1}^{n}x(i)y(i)$​

特殊情况：$⟨\mathbf{x},\mathbf{x}⟩={\mathbf{x}}^{\top }\mathbf{x}={\sum }_{i=1}^{n}x(i{)}^2=\Vert \mathbf{x}{\Vert }^2$

在距离中的应用：$⟨\mathbf{x}-\mathbf{y},\mathbf{x}-\mathbf{y}⟩=(\mathbf{x}-\mathbf{y}{)}^{\top }(\mathbf{x}-\mathbf{y})={\sum }_{i=1}^n[x(i)-y(i){]}^2=\Vert \mathbf{x}-\mathbf{y}{\Vert }^2$

向量的方向性对于数据空间位置，特别是数据集特征之间的相关性的衡量有重要的意义，且这种衡量可以通过射线之间的夹角来完成。两个向量的夹角越小，即原点和两个数据点越近似在一条直线上，则说明两个特征向量的线性相关性非常强。对于这一现象，我们在中学阶段已经接触过，当两个向量 $\mathbf{x}$​ 和 $\mathbf{y}$​ 相互垂直时，其内积满足：$⟨\mathbf{x},\mathbf{y}⟩=0$​。将向量的垂直关系进一步推广到任意夹角 $\theta$​，则可获得向量的另一个内积公式：
$$⟨\mathbf{x},\mathbf{y}⟩=\Vert \mathbf{x}\Vert \cdot \Vert \mathbf{y}\Vert \cdot \cos \theta$$

如图所示，O,X,Y三点是否在一条直线附近（或称 $OX$​ 和 $OY$​ 可以线性表出，即存在非零常数 $\alpha$​ 满足 $OY=\alpha \cdot OY$ )，这种度量线性相关性的量即是内积，与两个向量的长度和夹角的余弦有直接关系。

公式两边同时除以向量 $\mathbf{y}$ 的长度 $\Vert \mathbf{y}\Vert$​ 得，
$$⟨\mathbf{x},\hat{\mathbf{y}}⟩=⟨\mathbf{x},\frac{\mathbf{y}}{\Vert \mathbf{y}\Vert }⟩=\Vert \mathbf{x}\Vert \cdot \cos \theta$$
向量 $\mathbf{x}$​ 与单位向量 $\hat{\mathbf{y}}$​ 的内积是直角三角形斜边长度与夹角余弦的乘积，数值上等于灰色线段的长度，我们称之为向量 $\mathbf{x}$​ 在向量 $\mathbf{y}$​ 上的投影。内积的这种投影的应用在后续度量点到直线的距离和向量位置关系的时候至关重要，是模型建立的基础性应用。

公式两边同时除以向量 $\mathbf{x}$ 的长度 $\Vert \mathbf{x}\Vert$ 和向量 $\mathbf{y}$ 的长度 $\Vert \mathbf{y}\Vert$ 得，
$$⟨\hat{\mathbf{x}},\hat{\mathbf{y}}⟩=⟨\frac{\mathbf{x}}{\Vert \mathbf{x}\Vert },\frac{\mathbf{y}}{\Vert \mathbf{y}\Vert }⟩=\cos \theta$$
公式(2-7)在不考虑向量的长度因素情况下只考虑夹角，则两个单位向量的内积退化成夹角的余弦值，如图2-7 ©所示。

2.3 基于矩阵的距离运算

在做分类时，常常需要估算两个样本间的相似性度量（SimilarityMeasurement），这时经常就用到两个样本间的“距离”(Distance)，采用什么样的方法计算距离是很讲究，甚至关系到分类的正确与否。经常使用的度量方法是欧式距离，欧氏距离是最易于理解的一种距离计算方法，源自欧氏空间中两点间的距离公式。

给定 $m\times n$ 阶矩阵 $\mathbf{X}$，满足 $\mathbf{X}=[{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_n]$，其中， ${\mathbf{x}}_i\in {\mathbb{R}}^m$，则各向量（样本点）的距离定义为
$$D_{ij}=\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert =\sqrt{\sum _{t=1}^m(x_{i,t}-x_{j,t}{)}^2}$$
由于在机器学习中所用到的距离都是距离的平方的形式，因此，这里提供 4 中编程方法来实现距离的计算：

方法一：标准方法是通过使用两层 for 循环来实现
$$D_{ij}^2=\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2=\sum _{t=1}^m(x_{i,t}-x_{j,t}{)}^2$$
方法二：利用矩阵内积计算 $D_{ij}$，使用 numpy 的 norm 方法，这个方法从数学上讲，其计算公式是：
$$D_{ij}^2=\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2=({\mathbf{x}}_i-{\mathbf{x}}_j{)}^{\top }({\mathbf{x}}_i-{\mathbf{x}}_j)$$
方法三：避免循环内点积运算，减少 dot 调用次数

尽管 numpy 底层可能对点积运算做了优化，但还可以进一步优化。将向量差的内积进一步分解：
$$\begin{array}{rl}{D}_{ij}^2& =\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2\\ & =({\mathbf{x}}_i-{\mathbf{x}}_j{)}^{\top }({\mathbf{x}}_i-{\mathbf{x}}_j)\\ & ={\mathbf{x}}_i^{\top }{\mathbf{x}}_i-2{\mathbf{x}}_i^{\top }{\mathbf{x}}_j+{\mathbf{x}}_j^{\top }{\mathbf{x}}_j\end{array}$$
其中，${\mathbf{x}}_i^{\top }{\mathbf{x}}_i,{\mathbf{x}}_i^{\top }{\mathbf{x}}_j,{\mathbf{x}}_j^{\top }{\mathbf{x}}_j$ 均属于 Gram 矩阵 $\mathbf{G}={\mathbf{X}}^{\top }\mathbf{X}$ 中的元素，可通过 for 循环进行赋值
$$D_{ij}^2={\mathbf{G}}_{ii}-2{\mathbf{G}}_{ij}+{\mathbf{G}}_{jj}$$
方法四：利用复制对角向量避免for循环

由于 $D_{ij}^2={\mathbf{x}}_i^{\top }{\mathbf{x}}_i-2{\mathbf{x}}_i^{\top }{\mathbf{x}}_j+{\mathbf{x}}_j^{\top }{\mathbf{x}}_j$ 可通过构造矩阵 $\mathbf{H}=[\text{diag}(\mathbf{G}),\cdots ,\text{diag}(\mathbf{G})]$ 计算 距离矩阵的平方
$${\mathbf{D}}^2=\mathbf{H}+{\mathbf{H}}^{\top }-2\mathbf{G}$$

import numpy as np
import numpy.linalg as la
import time
 
X = np.array([range(0, 500), range(500, 1000)])
m, n = X.shape
 
#方法1：标准方法使用两层循环计算Dij
#时间复杂度O(n*n)
t = time.time()
D = np.zeros([n, n])
for i in range(n):
    for j in range(i + 1, n):
        D[i, j] = la.norm(X[:, i] - X[:, j]) ** 2
        D[j, i] = D[i, j]
print(time.time() - t)
 
 
#方法2：利用矩阵内积dot计算Dij
# 时间复杂度O(n*n)*O(m)
t = time.time()
D = np.zeros([n, n])
for i in range(n):
    for j in range(i + 1, n):
        d = X[:, i] - X[:, j]
        D[i, j] = np.dot(d, d)
        D[j, i] = D[i, j]
print(time.time() - t)
 
 
#方法3：避免循环内点积运算，减少dot调用次数
# 时间复杂度O(n*n)
t = time.time()
G = np.dot(X.T, X)
D = np.zeros([n, n])
for i in range(n):
    for j in range(i + 1, n):
        D[i, j] = G[i, i] - G[i, j] * 2 + G[j,j]
        D[j, i] = D[i, j]
print(time.time() - t)
 
 
#方法4：利用重复操作替代外部循环
t = time.time()
G = np.dot(X.T, X)
#把G对角线元素拎出来，列不变，行复制n遍。
H = np.tile(np.diag(G), (n, 1))
D = H + H.T - G * 2
print(time.time() - t)

结果

0.6473026275634766
0.2762320041656494
0.12765932083129883
0.0029916763305664062

2.4 优化：牛顿迭代和梯度下降算法

导数定义(定义要精确)
$$f^{\prime }(x)=\underset{x\to x_0}{\lim }\frac{f(x)-f(x_0)}{x-x_0}$$

即
$$f(x)=f(x_0)+f^{\prime }(x)(x-x_0)+o((x-x_0{)}^2)$$

泰勒展开式
$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+f^{\prime \prime }(x_0)(x-x_0{)}^2+o((x-x_0{)}^2)$$

牛顿迭代法
从泰勒展开式到牛顿算法

泰勒展开式
$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+f^{\prime \prime }(x_0)(x-x_0{)}^2+o((x-x_0{)}^2)$$

当需要求$y=f(x)$的根时，即$f(x)=0$

只取泰勒展开式的前两项作为近似，则
$$f(x_0)+f^{\prime }(x_0)(x-x_0)\approx 0$$
得
$$x\approx x_0-\frac{f(x_0)}{f^{\prime }(x_0)}$$

迭代格式为：
$$x_{n+1}:=x_n-\frac{f(x_n)}{f^{\prime }(x_n)}$$
从泰勒展开式到牛顿算法

泰勒展开式
$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+f^{\prime \prime }(x_0)(x-x_0{)}^2+o((x-x_0{)}^2)$$

当需要求$y=f(x)$的极值时，即$f^{\prime }(x)=0$，则可把$f(x)$看作$(x-x_0)$的二次函数，即求

$$\frac{f^{\prime \prime }(x_0)}{2}(x-x_0{)}^2+f^{\prime }(x_0)(x-x_0)+f(x_0)$$

的极值

则
$$x-x_0=-\frac{f^{\prime }(x_0)}{f^{\prime \prime }(x_0)}$$

迭代格式为：
$$x_{n+1}:=x_n-\frac{f^{\prime }(x_n)}{f^{\prime \prime }(x_n)}$$

梯度下降法
求$y=f(x)$的极值

$$x_{n+1}:=x_n-\alpha f^{\prime }(x_n)$$

其中，$\alpha$是步长，负梯度方向$-f^{\prime }(x_n)$为下降方向

# 梯度下降法的python实现，梯度下降算法是神经网络、深度学习的基础
# 本脚本通过梯度下降算法求函数y(x)的最小值
# 作者：MR_LeeCZ

import numpy as np
import matplotlib.pyplot as plt

def y(x):  # 定义函数，求函数的极小值
    y = (x-10)*(x-10) + 10*np.sin(x) - 3*x +60
    return y


def dy(x):  # 函数y(x)的导数
    dy = 2*(x-10) + 10*np.cos(x) -3
    return dy

def gradient_descent(x0, a, d0):  # 梯度下降法，x0为初始值，a为学习率，d0为算法的收敛条件
    value_appr = x0
    for i in range(1000):  # 迭代1000次，无论是否收敛都将终止程序
        d = y(x0) - y(x0-a*dy(x0)) # 更新前后函数值的增减幅度，确定是否停机
        if d < d0:  # 判断是否满足收敛条件
            break
        else:
            x0 = x0 - a*dy(x0)  # x0通过梯度更新，下降最快
            value_appr = np.append(value_appr,x0)

    return x0, value_appr

x0, xs = gradient_descent(0, 0.05, 0.0001)

x = np.linspace(0, 20, 40)
y_fun = y(x)
y_op = y(xs)

plt.plot(x,y_fun)
plt.scatter(xs,y_op,c='r')
plt.show()

print('最优解为: {x_hat}，相应的最优值为：{y_hat}'.format(x_hat=xs[-1],y_hat=y_op[-1]))

最优解为: 11.076141044662462，相应的最优值为：17.96209387410127

)

x = np.linspace(0, 20, 40)
y_fun = y(x)
y_op = y(xs)

plt.plot(x,y_fun)
plt.scatter(xs,y_op,c=‘r’)
plt.show()

print(‘最优解为: {x_hat}，相应的最优值为：{y_hat}’.format(x_hat=xs[-1],y_hat=y_op[-1]))

最优解为: 11.076141044662462，相应的最优值为：17.96209387410127