Pytorch总结十四之优化算法:梯度下降法、动量法
Pytorch总结十四之优化算法:梯度下降法、动量法
- 在一个深度学习问题中,我们会预先定义一个损失函数。有了损失函数以后,可以使用优化算法试图将其最小化。在优化中,这样的损失函数通常被称作优化问题的目标函数(objective function)。
- 依据惯例,优化算法通常只考虑最小化目标函数。
- 其实,任何最大化问题都可以很容易的转化为最小化问题,秩序令目标函数的相反数成为新的目标函数即可。
1.优化与深度学习
- 由于优化算法的⽬标函数通常是⼀个基于训练数据集的损失函数,优化的⽬标在于降低训练误差。
- ⽽深度学习的⽬标在于降低泛化误差。为了降低泛化误差,除了使⽤优化算法降低训练误差以外,还需要注意应对过拟合。
- 深度学习中绝⼤多数⽬标函数都很复杂。因此,很多优化问题并不存在解析解,⽽需要使⽤基于数值⽅法的优化算法找到近似解,即数值解。本书中讨论的优化算法都是这类基于数值⽅法的算法。为了求得最⼩化⽬标函数的数值解,我们将通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。
- 优化在深度学习中有很多挑战。下⾯描述了其中的两个挑战,即局部最⼩值和鞍点。为了更好地描述问
题,我们先导⼊本节中实验需要的包或模块。
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
from mpl_toolkits import mplot3d #三维画图
import numpy as np
1.1 局部极小值
def f(x):
return x*np.cos(np.pi*x)
d2l.set_figsize((4.5,2.5))
x=np.arange(-1.0,2.0,0.1)
fig, =d2l.plt.plot(x,f(x))
fig.axes.annotate('local minimum',xy=(-0.3,-0.25),xytext=(-0.77,-1.0),
arrowprops=dict(arrowstyle='->'))
fig.axes.annotate('global minimum',xy=(1.1,-0.95),xytext=(0.6,0.8),
arrowprops=dict(arrowstyle='->'))
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)')
d2l.plt.show()
若出现以下错误,需删除对应环境下\Library\bin文件夹中的这个libiomp5md.dll文件。
OMP: Error #15: Initializing libiomp5md.dll, but found libiomp5md.dll already initialized.
OMP: Hint This means that multiple copies of the OpenMP runtime have been linked into the program. That is dangerous, since it can degrade performance or cause incorrect results. The best thing to do is to ensure that only a single OpenMP runtime is linked into the process, e.g. by avoiding static linking of the OpenMP runtime in any library. As an unsafe, unsupported, undocumented workaround you can set the environment variable KMP_DUPLICATE_LIB_OK=TRUE to allow the program to continue to execute, but that may cause crashes or silently produce incorrect results. For more information, please see http://www.intel.com/software/products/support/.
修改后运行:
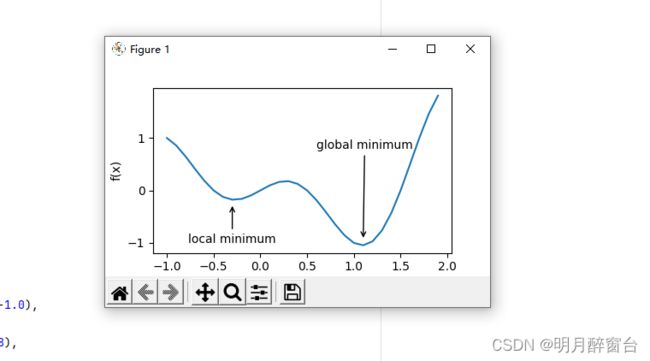
深度学习模型的目标函数可能有若干局部最优值。当一个优化问题的数值解在局部最优姐附近时,由于目标函数有关解的梯度接近或者变成零,最终迭代求得的数值解可能只令目标函数局部最小化而非全局最小化。
1.2 鞍点
- 鞍点(Saddle point)在微分方程中,沿着某一方向是稳定的,另一条方向是不稳定的奇点,叫做鞍点。在泛函中,既不是极大值点也不是极小值点的临界点,叫做鞍点。在矩阵中,一个数在所在行中是最大值,在所在列中是最小值,则被称为鞍点。在物理上要广泛一些,指在一个方向是极大值,另一个方向是极小值的点。

#鞍点
x = np.arange(-2.0, 2.0, 0.1)
fig, = d2l.plt.plot(x, x**3)
fig.axes.annotate('saddle point', xy=(0, -0.2), xytext=(-0.52,
-5.0),
arrowprops=dict(arrowstyle='->'))
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)');
d2l.plt.show()
#图2
x, y = np.mgrid[-1: 1: 31j, -1: 1: 31j]
z = x**2 - y**2
ax = d2l.plt.figure().add_subplot(111, projection='3d')
ax.plot_wireframe(x, y, z, **{'rstride': 2, 'cstride': 2})
ax.plot([0], [0], [0], 'rx')
ticks = [-1, 0, 1]
d2l.plt.xticks(ticks)
d2l.plt.yticks(ticks)
ax.set_zticks(ticks)
d2l.plt.xlabel('x')
d2l.plt.ylabel('y')
d2l.plt.show()

在图的鞍点位置,⽬标函数在 x 轴⽅向上是局部最⼩值,但在 y 轴⽅向上是局部最⼤值。
假设⼀个函数的输⼊为 k 维向量,输出为标量,那么它的海森矩阵(Hessian matrix)有 k 个特征值。该
函数在梯度为0的位置上可能是局部最⼩值、局部最⼤值或者鞍点。
- 当函数的海森矩阵在梯度为零的位置上的特征值全为正时,该函数得到局部最⼩值。
- 当函数的海森矩阵在梯度为零的位置上的特征值全为负时,该函数得到局部最⼤值。
- 当函数的海森矩阵在梯度为零的位置上的特征值有正有负时,该函数得到鞍点。
随机矩阵理论告诉我们,对于⼀个⼤的⾼斯随机矩阵来说,任⼀特征值是正或者是负的概率都是0.5。那么,以上第⼀种情况的概率为 0.5^k。由于深度学习模型参数通常都是⾼维的( 很⼤),⽬标函数的鞍点通常⽐局部最⼩值更常⻅。
1.3 小结
- 由于优化算法的⽬标函数通常是⼀个基于训练数据集的损失函数,优化的⽬标在于降低训练误差。
- 由于深度学习模型参数通常都是⾼维的,⽬标函数的鞍点通常⽐局部最⼩值更常⻅。
2.梯度下降和随机梯度下降
-> gradient descent and stochastic gradient descent
2.1 一维梯度下降
import numpy as np
import torch
import math
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
def gd(eta):
x = 10
results = [x]
for i in range(10):
x -= eta * 2 * x # f(x) = x * x的导数为f'(x) = 2 * x
results.append(x)
print('epoch 10, x:', x)
return results
res = gd(0.2)
输出:
epoch 10, x: 0.06046617599999997
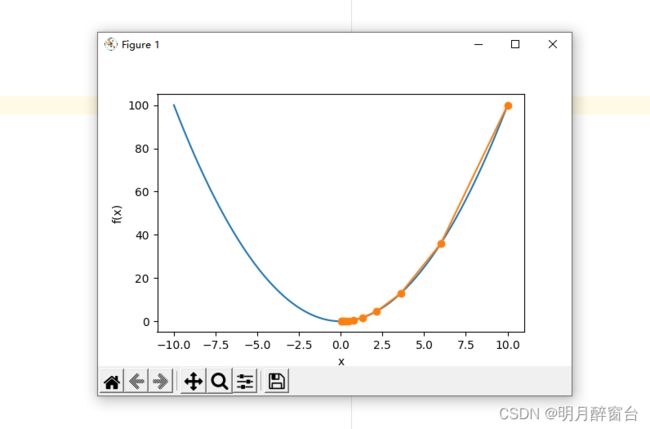
下⾯将绘制出⾃变量 x 的迭代轨迹:
def show_trace(res):
n = max(abs(min(res)), abs(max(res)), 10)
f_line = np.arange(-n, n, 0.1)
d2l.set_figsize()
d2l.plt.plot(f_line, [x * x for x in f_line])
d2l.plt.plot(res, [x * x for x in res], '-o')
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)')
d2l.plt.show()
show_trace(res)
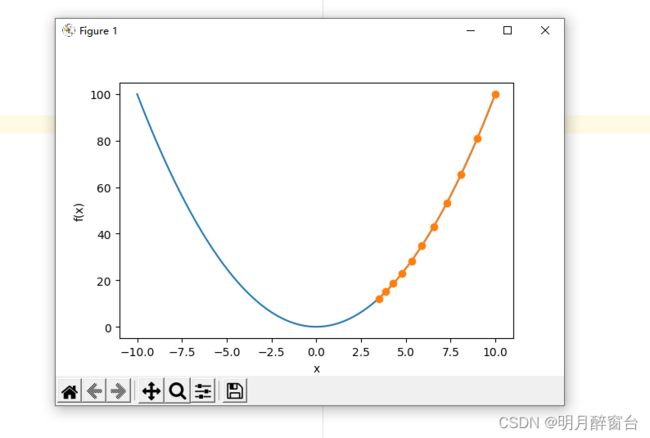
2.2 学习率
show_trace(gd(0.05))
输出:
epoch 10, x: 3.4867844009999995
show_trace(gd(1.1))
输出:
epoch 10, x: 61.917364224000096
2.3 多维梯度下降
def train_2d(trainer): # 本函数将保存在d2lzh_pytorch包中⽅便以后使⽤
x1, x2, s1, s2 = -5, -2, 0, 0 # s1和s2是⾃变量状态,本章后续⼏节会使⽤
results = [(x1, x2)]
for i in range(20):
x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
results.append((x1, x2))
print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
return results
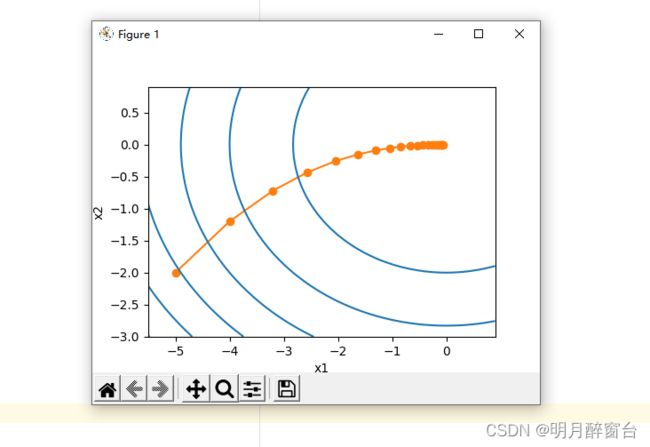
def show_trace_2d(f, results): # 本函数将保存在d2lzh_pytorch包中⽅便以后使⽤
d2l.plt.plot(*zip(*results), '-o', color='#ff7f0e')
x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0,1.0, 0.1))
d2l.plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
d2l.plt.xlabel('x1')
d2l.plt.ylabel('x2')
d2l.plt.show()
eta = 0.1
def f_2d(x1, x2): # ⽬标函数
return x1 ** 2 + 2 * x2 ** 2
def gd_2d(x1, x2, s1, s2): #梯度下降:沿梯度方向求解目标函数最小值
return (x1 - eta * 2 * x1, x2 - eta * 4 * x2, 0, 0)
show_trace_2d(f_2d, train_2d(gd_2d))
输出:
epoch 20, x1 -0.057646, x2 -0.000073
2.4 随机梯度下降
这意味着,平均来说,随机梯度是对梯度的⼀个良好的估计。
下⾯我们通过在梯度中添加均值为0的随机噪声来模拟随机梯度下降,以此来⽐较它与梯度下降的区别。
def sgd_2d(x1, x2, s1, s2):
return (x1 - eta * (2 * x1 + np.random.normal(0.1)),
x2 - eta * (4 * x2 + np.random.normal(0.1)), 0, 0)
show_trace_2d(f_2d, train_2d(sgd_2d))
输出:
epoch 20, x1 -0.236495, x2 0.225379

可以看到,随机梯度下降中⾃变量的迭代轨迹相对于梯度下降中的来说更为曲折。这是由于实验所添加
的噪声使模拟的随机梯度的准确度下降。在实际中,这些噪声通常指训练数据集中的⽆意义的⼲扰。
2.5 小结
- 使⽤适当的学习率,沿着梯度反⽅向更新⾃变量可能降低⽬标函数值。梯度下降重复这⼀更新过程直到得到满⾜要求的解。
- 学习率过⼤或过⼩都有问题。⼀个合适的学习率通常是需要通过多次实验找到的。
- 当训练数据集的样本较多时,梯度下降每次迭代的计算开销较⼤,因⽽随机梯度下降通常更受⻘睐。
3.小批量随机梯度下降
3.1 读取数据
本章⾥我们将使⽤⼀个来⾃NASA的测试不同⻜机机翼噪⾳的数据集来⽐较各个优化算法 。我们使⽤该数据集的前1,500个样本和5个特征,并使⽤标准化对数据进⾏预处理。
⻜机机翼噪⾳数据集:https://archive.ics.uci.edu/ml/datasets/Airfoil+Self-Noise
import numpy as np
import time
import torch
from torch import nn, optim
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
def get_data_ch7(): # 本函数已保存在d2lzh_pytorch包中⽅便以后使⽤
data = np.genfromtxt('../../data/airfoil_self_noise.dat',delimiter='\t')
data = (data - data.mean(axis=0)) / data.std(axis=0)
return torch.tensor(data[:1500, :-1], dtype=torch.float32), \
torch.tensor(data[:1500, -1], dtype=torch.float32) # 前1500个样本(每个样本5个特征)
features, labels = get_data_ch7()
print(features.shape) # torch.Size([1500, 5])
输出:
torch.Size([1500, 5])
3.2 简洁实现
在PyTorch⾥可以通过创建 optimizer 实例来调⽤优化算法。这能让实现更简洁。下⾯实现⼀个通⽤的训练函数,它通过优化算法的函数 optimizer_fn 和超参数optimizer_hyperparams 来创建optimizer 实例。
# 本函数与原书不同的是这⾥第⼀个参数优化器函数⽽不是优化器的名字
# 例如: optimizer_fn=torch.optim.SGD, optimizer_hyperparams={"lr":0.05}
def train_pytorch_ch7(optimizer_fn, optimizer_hyperparams,features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net = nn.Sequential(nn.Linear(features.shape[-1], 1))
loss = nn.MSELoss()
optimizer = optimizer_fn(net.parameters(),**optimizer_hyperparams)
def eval_loss():
return loss(net(features).view(-1), labels).item() / 2
ls = [eval_loss()]
data_iter = torch.utils.data.DataLoader(
torch.utils.data.TensorDataset(features, labels),
batch_size, shuffle=True)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
# 除以2是为了和train_ch7保持⼀致, 因为squared_loss中除了2
l = loss(net(X).view(-1), y) / 2
optimizer.zero_grad()
l.backward()
optimizer.step()
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss())
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() -
start))
d2l.set_figsize()
d2l.plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
d2l.plt.xlabel('epoch')
d2l.plt.ylabel('loss')
d2l.plt.show()
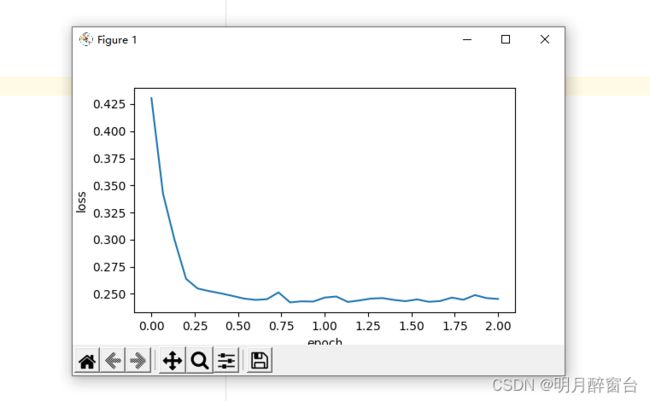
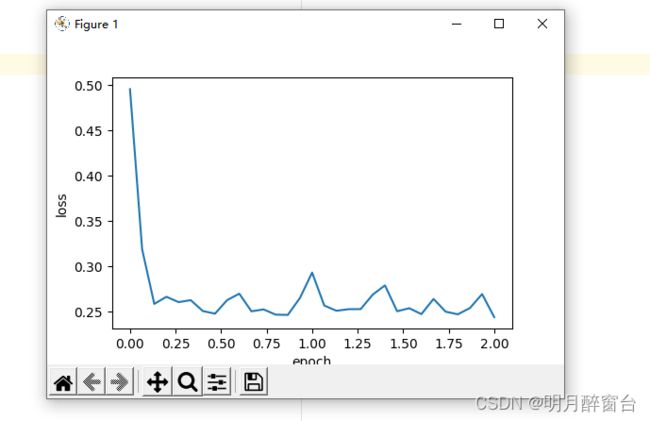
使⽤PyTorch重复上⼀个实验
train_pytorch_ch7(optim.SGD, {"lr": 0.05}, features, labels, 10)
输出:
loss: 0.245491, 0.044150 sec per epoch
3.3 小结
- ⼩批量随机梯度每次随机均匀采样⼀个⼩批量的训练样本来计算梯度。
- 在实际中,(⼩批量)随机梯度下降的学习率可以在迭代过程中⾃我衰减。
- 通常,⼩批量随机梯度在每个迭代周期的耗时介于梯度下降和随机梯度下降的耗时之间。
4.动量法
⽬标函数有关⾃变量的梯度代表了⽬标函数在⾃变量当前位置下降最快的⽅向。因此,梯度下降也叫作最陡下降(steepest descent)。在每次迭代中,梯度下降根据⾃变量当前位置,沿着当前位置的梯度更新⾃变量。然⽽,如果⾃变量的迭代⽅向仅仅取决于⾃变量当前位置,这可能会带来⼀些问题。
4.1 梯度下降法的问题
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
import torch
eta = 0.4 # 学习率
def f_2d(x1, x2):
return 0.1 * x1 ** 2 + 2 * x2 ** 2
def gd_2d(x1, x2, s1, s2):
return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)
d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))
输出:
epoch 20, x1 -0.943467, x2 -0.000073
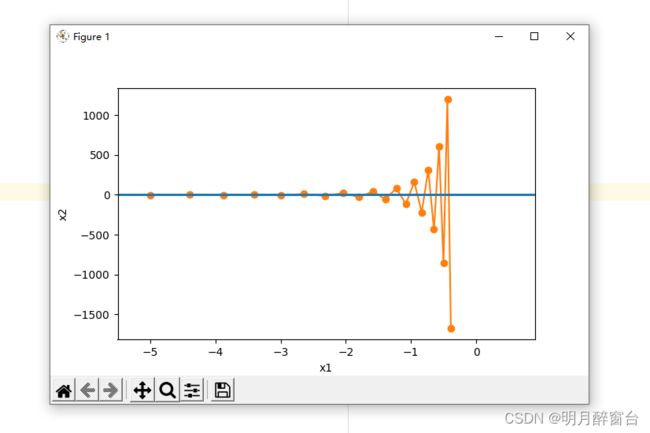
下⾯我们试着将学习率调得稍⼤⼀点,此时⾃变量在竖直⽅向不断越过最优解并逐渐发散。
eta = 0.6
d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))
输出:
epoch 20, x1 -0.387814, x2 -1673.365109
4.2 动量法

在解释动量法的数学原理前,让我们先从实验中观察梯度下降在使⽤动量法后的迭代轨迹。
#动量法
def momentum_2d(x1, x2, v1, v2):
v1 = gamma * v1 + eta * 0.2 * x1
v2 = gamma * v2 + eta * 4 * x2
return x1 - v1, x2 - v2, v1, v2
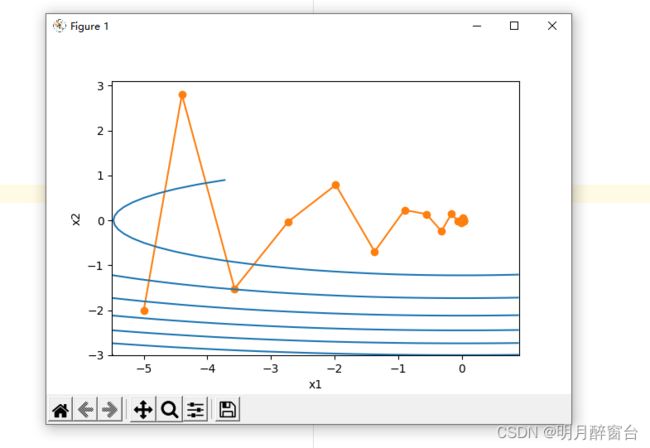
eta, gamma = 0.4, 0.5
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))
输出:
epoch 20, x1 -0.062843, x2 0.001202
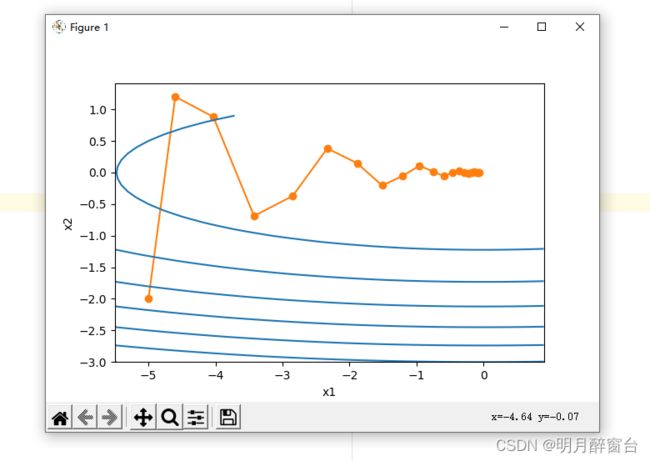
eta = 0.6
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))
输出:
epoch 20, x1 0.007188, x2 0.002553
4.3算法实现
- 从零实现:
相对于⼩批量随机梯度下降,动量法需要对每⼀个⾃变量维护⼀个同它⼀样形状的速度变量,且超参数⾥多了动量超参数。实现中,我们将速度变量⽤更⼴义的状态变量states表示。
features, labels = d2l.get_data_ch7()
def init_momentum_states():
v_w = torch.zeros((features.shape[1], 1), dtype=torch.float32)
v_b = torch.zeros(1, dtype=torch.float32)
return (v_w, v_b)
def sgd_momentum(params, states, hyperparams):
for p, v in zip(params, states):
v.data = hyperparams['momentum'] * v.data + hyperparams['lr'] * p.grad.data
p.data -= v.data
我们先将动量超参数 momentum 设0.5,这时可以看成是特殊的⼩批量随机梯度下降:其⼩批量随机梯度为最近2个时间步的2倍⼩批量梯度的加权平均。
d2l.train_ch7(sgd_momentum, init_momentum_states(),{'lr': 0.02, 'momentum': 0.5}, features, labels)
输出:
loss: 0.244133, 0.049868 sec per epoch
#test1
d2l.train_ch7(sgd_momentum, init_momentum_states(),{'lr': 0.02, 'momentum': 0.9}, features, labels)
#test2
d2l.train_ch7(sgd_momentum, init_momentum_states(),{'lr': 0.004, 'momentum': 0.9}, features, labels)
- 简洁实现:
在PyTorch中,只需要通过参数momentum来指定动量超参数即可使⽤动量法:
d2l.train_pytorch_ch7(torch.optim.SGD, {'lr': 0.004, 'momentum':0.9},features, labels)
输出:
loss: 0.242355, 0.052859 sec per epoch
4.4 小结
- 动量法使⽤了指数加权移动平均的思想。它将过去时间步的梯度做了加权平均,且权重按时间步指数衰减。
- 动量法使得相邻时间步的⾃变量更新在⽅向上更加⼀致。