python之建模数值逼近问题
数值插入
在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。
一维插值
一.插值函数经过样本点,拟合函数一般基于最小二乘法尽量靠近所有样本点穿过。常见插值方法有拉格朗日插值法、分段插值法、样条插值法:
2.分段插值:虽然收敛,但光滑性较差。
3.样条插值:由于样条插值可以使用低阶多项式样条实现较小的插值误差,这样就避免了龙格现象。
线性插值与样条插值
样例1:某电学元件的电压数据记录在0~2.25TA范围与电流关系满足正弦函数,分别用线性插值和样条插值方法给出经过数据点的数值逼近函数曲线。
代码如下:
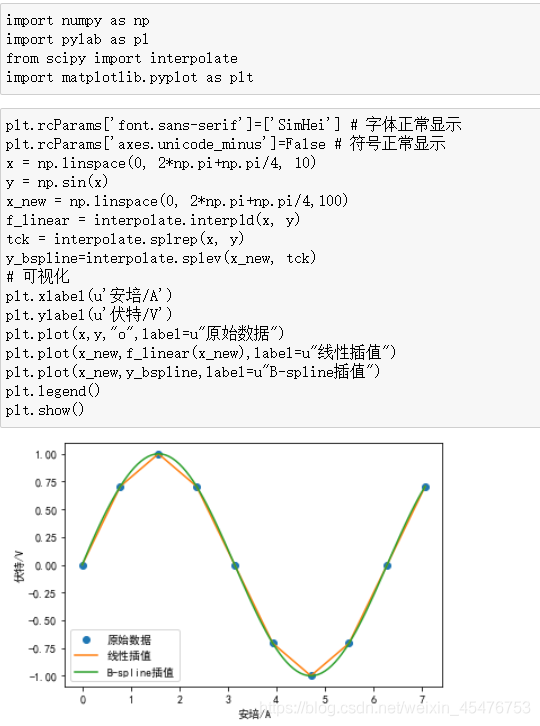
高阶样条插值
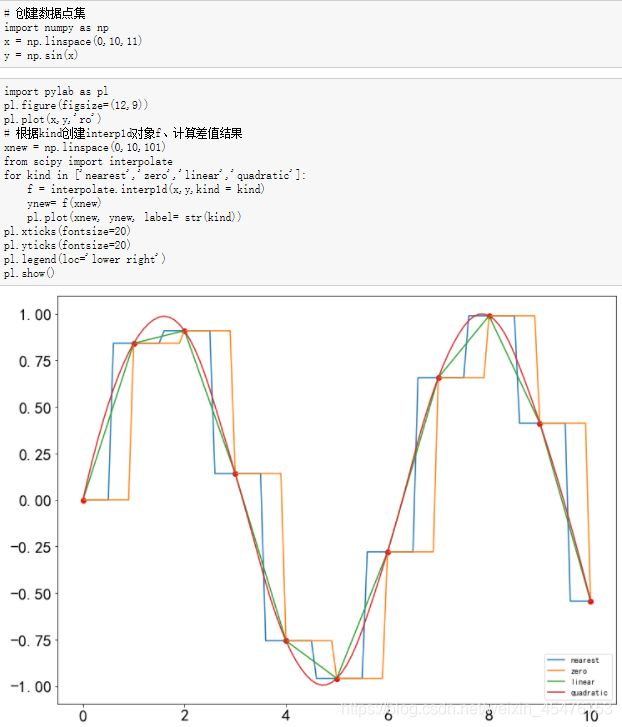
样例2:某电学元件的电压数据记录在0~10A范围与电流关系满足正弦函数,分别用0-5阶样条插值方法给出经过数据点的数值逼近函数曲线。
代码如下:
二维插值
方法与一维数据插值类似,为二维样条插值。
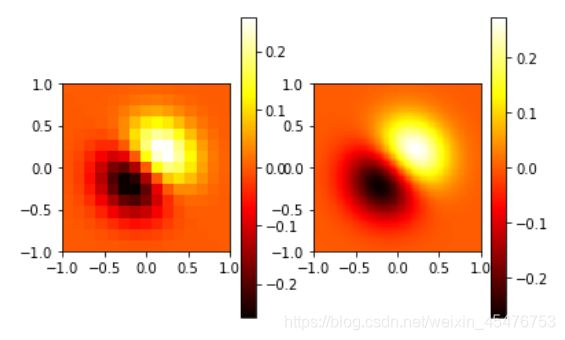
样例3:某二维图像表达式为(x +y)e-5(x2+y2),完成图像的二维插值使其变清晰。
代码如下:
import numpy as np
from scipy import interpolate
import pylab as pl
import matplotlib as mpl
def func(x,y):
return (x+y)*np.exp(-5.0*(x**2+y**2))
# X-Y轴分为15*15的网格
y,x = np.mgrid[-1:1:15j, -1:1:15j]
# 计算每个网格点上的函数值
fvals = func(x, y)
# 三次样条二维插值
newfunc = interpolate.interp2d(x,y,fvals,kind='cubic')
# 计算100*100网络上插值
xnew=np.linspace(-1,1,100)
ynew=np.linspace(-1,1,100)
fnew = newfunc(xnew, ynew)
# 可视化
# 让imshow的参数interpolation设置为'nearest'方便比较插值处理
pl.subplot(121)
im1 =pl.imshow(fvals,extent=[-1,1,-1,1],cmap=mpl.cm.hot, interpolation='nearest', origin="lower")
pl.colorbar(im1)
pl.subplot(122)
im2=pl.imshow(fnew, extent=[-1,1,-1,1],cmap=mpl.cm.hot, interpolation='nearest', origin="lower")
pl.colorbar(im2)
pl.show()
结果如下:
三维插值
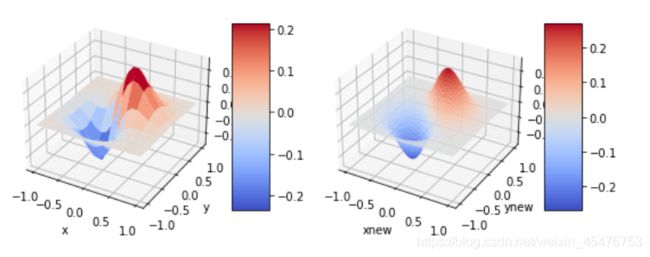
样例4:某图像表达式为(x +y)e-5(x2+y2),完成三维图像的二维插值可视化。
代码如下:
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
from scipy import interpolate
import matplotlib.cm as cm
import matplotlib.pyplot as plt
def func(x ,y):
return (x+y)*np.exp(-5.0*(x**2+y**2))
#X-Y轴分为20*20的网络
x = np.linspace(-1,1,20)
y = np.linspace(-1,1,20)
x, y =np.meshgrid(x,y)
fvals = func(x,y)
# 画分图1
fig =plt.figure(figsize=(9,6))
ax = plt.subplot(1,2,1,projection='3d')
# rstride行跨度 cstride列跨度 antialised抗锯齿效果
surf = ax.plot_surface(x,y,fvals,rstride=2,cstride=2,cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
plt.colorbar(surf,shrink=0.5,aspect=5) #添加颜色标注
#二维插值
newfunc = interpolate.interp2d(x,y,fvals,kind='cubic')
# 计算100*100网络上的插值
xnew = np.linspace(-1,1,100)
ynew = np.linspace(-1,1,100)
fnew = newfunc(xnew,ynew)
xnew,ynew=np.meshgrid(xnew,ynew)
ax2 = plt.subplot(1,2,2,projection='3d')
surf2 = ax2.plot_surface(xnew,ynew,fnew,rstride=2,cstride=2,cmap=cm.coolwarm,linewidth=0.5,antialiased=True)
ax2.set_xlabel('xnew')
ax2.set_ylabel('ynew')
ax2.set_zlabel('fnew(x,y)')
plt.colorbar(surf2,shrink=0.5,aspect=5)
plt.show()
最小二乘拟合
拟合指的是已知某函数的若干离散函数值{f1,f2,…,fn},通过调整该函数中若干待定系数f(λ1,λ2,…λn),使得该函数与已知点集的差别(最小二乘意义)最小。如果待定函数是线性,就叫线性拟合或者线性回归(主要在统计中),否则叫作非线性拟合或者非线性回归。表达式也可以是分段函数,这种情况下叫作样条拟合。从几何意义上讲,拟合是给定了空间中的一些点,找到一个已知形式未知参数的连续曲面来最大限度地逼近这些点;而插值是找到一个(或几个分片光滑的)连续曲面来穿过这些点。选择参数c使得拟合模型与实际观测值在曲线拟合各点的残差(或离差)ek=yk一f(xk,c)的加权平方和达到最小,此时所求曲线称作在加权最小二乘意义下对数据的拟合曲线,这种方法叫做最小二乘法。
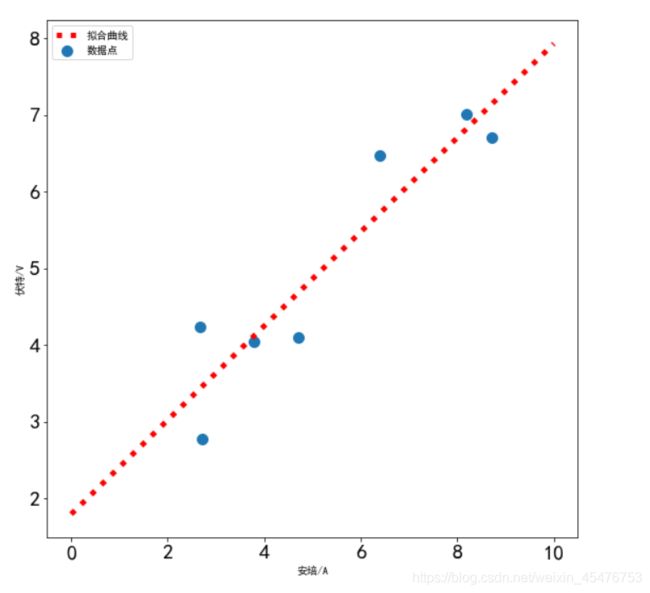
样例5:对下列电学元件的电压电流记录结果进行最小二乘拟合,绘制相应曲线。import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
plt.rcParams['font.sans-serif']=['SimHei'] # 字体正常显示
plt.rcParams['axes.unicode_minus']=False # 符号正常显示
plt.figure(figsize=(9,9))
X=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78])
Y=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])
#计算以p为参数的直线与原始数据之间误差
def f(p):
k,b=p
return(Y-(k*X)-b)
#leastsq使得f的输出数组的平方和最小,参数初始值为[1,0]
r=leastsq(f,[1,0])
k,b=r[0]
plt.scatter(X,Y,s=100,alpha=1.0,marker='o',label=u'数据点')
x=np.linspace(0,10,1000)
y=k*x+b
ax =plt.gca()
ax.get_xlabel()
ax.get_ylabel()
plt.plot(x, y, color='r',linewidth=5,linestyle=":" , markersize=20,label=u'拟合曲线')
plt.legend(loc=0, numpoints=1)
leg = plt.gca().get_legend ()
ltext = leg.get_texts ()
plt.setp(ltext, fontsize='xx-large')
plt.xlabel(u'安培/A')
plt.ylabel (u'伏特/V')
#plt.xlim(0, x.max() * 1.1)
#plt.ylim(0, y.max() * 1.1)
plt.xticks (fontsize=20)
plt.yticks (fontsize=20)
plt.legend ( loc='upper left' )
plt.show ()
结果如下: