python图像处理（十一）——图像锐化与边缘检测之Roberts算子、Prewitt算子、Sobel算子、Laplacian算子

在图像增强过程中，通常利用各类图像平滑算法消除噪声，图像的常见噪声主要有加性噪声、乘性噪声和量化噪声等。一般来说，图像的能量主要集中在其低频部分，噪声所在的频段主要在高频段，同时图像边缘信息也主要集中在其高频部分。这将导致原始图像在平滑处理之后，图像边缘和图像轮廓模糊的情况出现。为了减少这类不利效果的影响，就需要利用图像锐化技术，使图像的边缘变得清晰。

 

一、Roberts算子

Roberts算子又称交叉微分算法，它是基于交叉差分的梯度算法，通过局部差分计算检测边缘线条，常来处理具有陡峭的低噪声图像，当图像边缘接近于正负45，处理效果最佳。缺点是对边缘定位信息不太准确，提取的边缘线条较粗。Roberts算子模板分为水平方向和垂直方向。

在python中Roberts算子主要是通过Numpy定义模板，再调用OpenCV中的filter2D()函数实现边缘提取，该函数主要是利用内核实现对图像的卷积运算，其函数原型如下：

dst=cv.filter2D(src, ddepth, kernel[, dst[, anchor[, delta[, borderType]]]])

参数如下：

src	原图像
dst	目标图像，与原图像尺寸和通过数相同
ddepth	目标图像的所需深度
kernel	卷积核（或相当于相关核），单通道浮点矩阵;如果要将不同的内核应用于不同的通道，请使用拆分将图像拆分为单独的颜色平面，然后单独处理它们。
anchor	内核的锚点，指示内核中过滤点的相对位置;锚应位于内核中;默认值（-1，-1）表示锚位于内核中心。
detal	在将它们存储在dst中之前，将可选值添加到已过滤的像素中。类似于偏置。
borderType	像素外推法，参见BorderTypes

Roberts算法代码如下所示：

import cv2
import matplotlib.pyplot as plt
import numpy as np

#读取图像
image = cv2.imread('E:/pythonProject/12.png')
lena = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)

#灰度转化处理
grayImage = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

#roberts算子
kernelx = np.array([[-1, 0], [0, 1]], dtype= int)
kernely = np.array([[0, -1], [1, 0]], dtype= int)
x = cv2.filter2D(grayImage, cv2.CV_16S, kernelx)
y = cv2.filter2D(grayImage, cv2.CV_16S, kernely)

#转uint8
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)

#加权和
Roberts = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)

#显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']

#图像显示
titles = [u'原始图像', u'Robertes图像']
images = [lena, Roberts]

for i in range(2):
    plt.subplot(1, 2, i+1), plt.imshow(images[i], 'gray')
    plt.xticks([]), plt.yticks([])
    plt.title(titles[i])
plt.show()

输出结果如下所示：

 

二、Prewitt算子

Prewitt算子是一种图像边缘检测的微分算子，由于Prewitt算子采用3*3模板对区域中的像素进行计算，而Roberts算子的是利用2*2模板，因此，Prewitt算子边缘检测结果在水平方向和垂直方向均比Roberts算子更加明显。Prewitt算子适合用来处理噪声较多，灰度渐变的图像。

在python中,Prewitt算子处理过程与Roberts算子较为相似，主要是通过Numpy定义模板，再调用OpenCV中的filter2D()函数实现对图像的卷积运算，最终通过cv2.convertScaleAbs()，和cv2.addWeighted()实现图像边缘提取。

Prewitt算法代码如下所示：

import cv2
import numpy as np
import matplotlib.pyplot as plt

#输入图像
image = cv2.imread('E:/pythonProject/12.png')
lena = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)

#灰度转化处理
grayImage = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

#kernel
kernelX = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]],dtype= int)
kernelY = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]],dtype= int)
x = cv2.filter2D(grayImage, cv2.CV_16S, kernelX)
y = cv2.filter2D(grayImage, cv2.CV_16S, kernelY)

#转uint8
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)

#加权和
Prewitt = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)

#图象显示
plt.rcParams['font.sans-serif'] = ['SimHei']
titles = [u'原始图像', u'Prewitt图像']
images = [lena, Prewitt]

for i in range(2):
    plt.subplot(1, 2, i+1), plt.imshow(images[i], 'gray')
    plt.xticks([]), plt.yticks([])
    plt.title(titles[i])
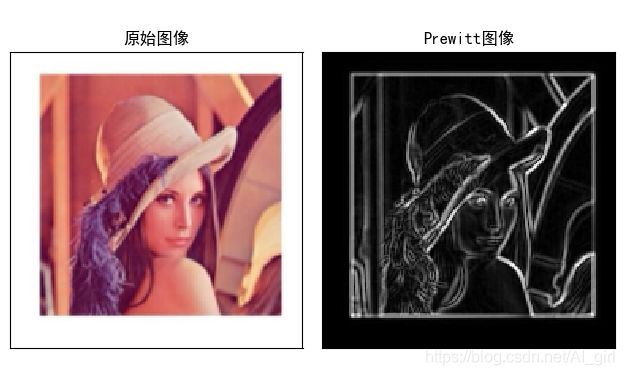
plt.show()

输出结果如下所示：

从其效果图输出可以明显看出，Prewitt算子在垂直方向和水平方向其边缘检测结果均比Roberts算子边缘检测轮廓要更明显。

 

三、Sobel算子

Sobel算子根据像素点上下、左右邻点灰度加权差，在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用，提供较为精确的边缘方向信息，边缘定位精度不够高。当对精度要求不是很高时，是一种较为常用的边缘检测方法。

函数原型：

sobelx = cv2.Sobel(img,cv2.CV_64F, 1, 0, ksize=3)

• img表示原图像
• 利用Sobel方法可以进行sobel边缘检测 img表示源图像，即进行边缘检测的图像 cv2.CV_64F表示64位浮点数即64float， 这里不使用numpy.float64，因为可能会发生溢出现象。
• 用cv的数据则会自动 第三和第四个参数分别是对X和Y方向的导数（即dx,dy），对于图像来说就是差分，这里1表示对X求偏导（差分），0表示不对Y求导（差分），其中，X还可以求2次导。 （注意：对X求导就是检测X方向上是否有边缘。）
• 第五个参数ksize是指核的大小。

在sobel处理之后还要用cv2.convertScaleAbs()求其绝对值，并将图像转化为uint8格式。

Sobel算法代码如下所示：

import cv2
import matplotlib.pyplot as plt

#读取图像
image = cv2.imread('E:/pythonProject/12.png')
lean = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)

#转灰度图像
grayImage = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

#Sobel算子
x = cv2.Sobel(grayImage, cv2.CV_16S, 1, 0)#对x一阶求导
y = cv2.Sobel(grayImage, cv2.CV_16S, 0, 1)#对y一阶求导
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
Sobel = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)

#图像输出
plt.rcParams['font.sans-serif'] = ['SimHei']
titles = [u'原始图像', u'Sobel图像']
images = [lean, Sobel]

for i in range(2):
    plt.subplot(1, 2, i+1), plt.imshow(images[i], 'gray')
    plt.xticks([]), plt.yticks([])
    plt.title(titles[i])
plt.show()

输出结果如下所示：

 

四、Laplacian算子

Laplace函数实现的方法是先用Sobel 算子计算二阶x和y导数，再求和。

函数原型：

dst = cv2.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])

必须的参数：

• scr是需要处理的图像；
• ddepth是图像的深度，-1表示采用的是与原图像相同的深度。目标图像的深度必须大于等于原图像的深度；

可选的参数：

• dst表示输出边缘图，其大小和通道数与输入图像相同；
• ksize是算子的大小，必须为1、3、5、7。默认为1。
• scale是缩放导数的比例常数，默认情况下没有伸缩系数；
• delta是一个可选的增量，将会加到最终的dst中，同样，默认情况下没有额外的值加到dst中；
• borderType是判断图像边界的模式。这个参数默认值为cv2.BORDER_DEFAULT。

Laplacian算子代码如下所示：

import cv2
import matplotlib.pyplot as plt

#读取图像
image = cv2.imread('E:/pythonProject/12.png')
lean = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)

#转灰度图像
grayImage = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

#拉普拉斯算法
dst = cv2.Laplacian(grayImage, cv2.CV_16S, ksize= 3)
Laplacian = cv2.convertScaleAbs(dst)

#图像输出
plt.rcParams['font.sans-serif'] = ['SimHei']
titles = [u'原始图像', u'Laplacian图像']
images = [lean, Laplacian]

for i in range(2):
    plt.subplot(1, 2, i+1), plt.imshow(images[i], 'gray')
    plt.xticks([]), plt.yticks([])
    plt.title(titles[i])
plt.show()

输出结果如下所示：

今天先写这么多，后期持续更新~