数据结构与算法--图
文章目录
- 前言
- 一、图的基本概念
-
- 1.什么是图
- 2.无向图(undirected graph)
- 3.有向图(directed graph)
- 4.顶点的度
-
- 4.1 度:无向图中,与某个顶点连接的边的数目。
- 4.2 入度:有向图中,以某个顶点为头的弧的数目。
- 4.3 出度:有向图中,以某个顶点为尾的弧的数目。
- 5.完全图
-
- 5.1 无向完全图
- 5.2 有向完全图
- 6.连通图
- 7.数组存储
-
- 7.1 无向图的数组存储主要有以下特性
- 7.2 有向图的数组存储主要有以下特性
- 7.3 数组存储方式优点
- 7.4 数组存储方式缺点
- 8.邻接表存储
-
- 8.1 无向图采用邻接表方式存储
- 8.2 有向图采用邻接表方式存储
- 总结
前言
图是数据结构中重要内容。相比于线性表与树,图的结构更为复杂。在线性表的存储结构中,数据直接按照前驱后继的线性组织形式排列。在树的结构中,数据节点以层的方式排列,节点与节点之间是一种层次关系。但是,在图的结构中数据之间可以有任意关系,这就使得图的数据结构相对复杂。
一、图的基本概念
1.什么是图
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V 是图 G 中顶点的集合,E 是图 G 中边的集合。
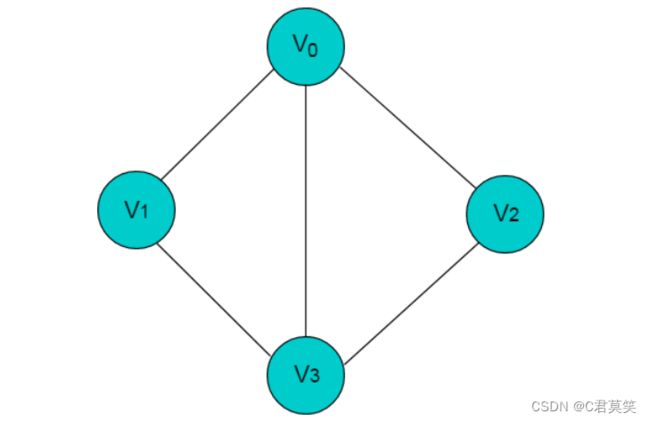
上图共有 V0,V1,V2,V3 这 4 个顶点,4 个顶点之间共有 5 条边。
注:
当线性表没有数据节点时,线性表为空表。 树中没有节点时,树为空树。 但是,在图中不允许没有顶点,但是可以没有边。
2.无向图(undirected graph)
无向图:图中顶点间的关系是无向对。无向图顶点间的关系称为边。

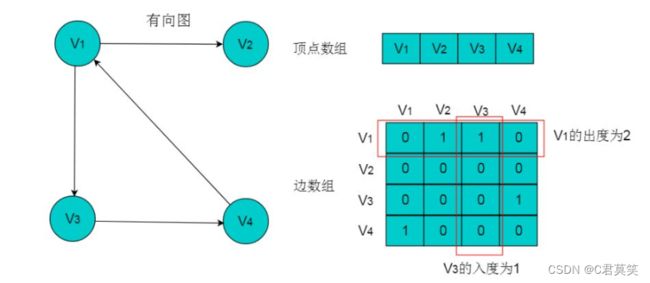
3.有向图(directed graph)
有向图:图中顶点间的关系是有向对。有向图顶点间的关系称为弧。
4.顶点的度
连接顶点的边的数量称为该顶点的度。顶点的度在有向图和无向图中具有不同的表示。对于无向图,一个顶点V的度比较简单,其是连接该顶点的边的数量,对于有向图要稍复杂些,根据连接顶点V的边的方向性,一个顶点的度有入度和出度之分。
4.1 度:无向图中,与某个顶点连接的边的数目。
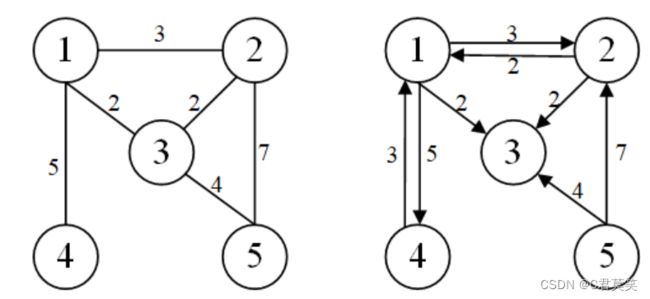
以上面的无向网为例,1,2,3的度均为3,4的度为1,5的度为2。
N个顶点的无向图,每个顶点的度最大为N-1。
4.2 入度:有向图中,以某个顶点为头的弧的数目。
4.3 出度:有向图中,以某个顶点为尾的弧的数目。
以上面有向图为例,1的入度为2,出度为3;3的入度为3,出度为0。
N个顶点的有向图,每个顶点的度最大为2(N-1)。
5.完全图
完全图:每个顶点都与其他顶点相邻接的图。
5.1 无向完全图
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。(含有n个顶点的无向完全图有(n×(n-1))/2条边)

5.2 有向完全图
在有向图中,如果任意两个顶点之间都存在方向互为相反的两条边,则称该图为有向完全图。(含有 n 个顶点的有向完全图有 n×(n-1) 条边)

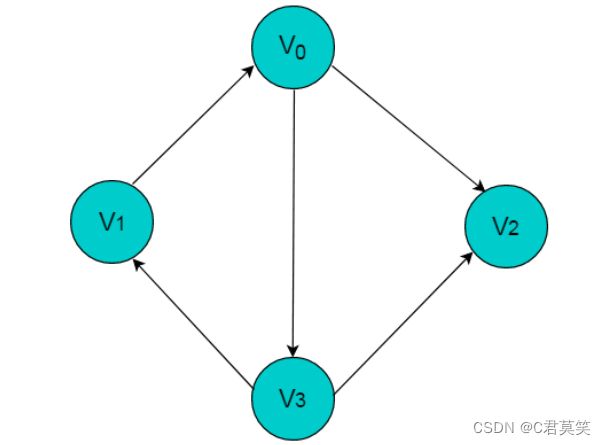
6.连通图
图中顶点A、B、C、D是连通的,但是其中任一顶点与顶点E或者顶点F之间没有路径,该图为非连通图。
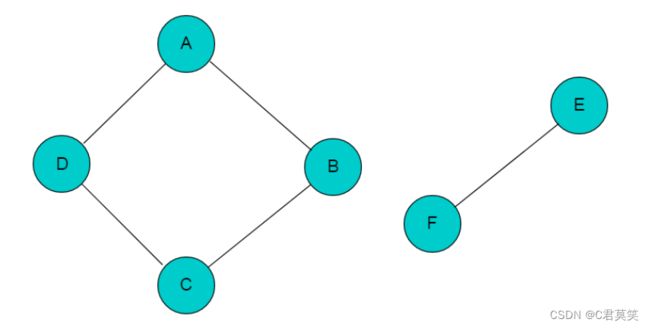
若添加顶点B与顶点F之间的邻接边,则图变为连通图。

7.数组存储
图的数组存储方式也称为邻接矩阵存储。图中的数据信息包括:顶点信息和描述顶点之间关系的边的信息,将这两种信息存储在数组中即为图的数组存储。
首先,创建顶点数组,顶点数组中存储的是图的顶点信息,采用一维数组的方式即可存储所有的顶点信息。存储图中边的信息时,由于边是描述顶点与顶点之间关系的信息,因此需要采用二维数组进行存储。
下图所示的无向图,采用数组存储形式如下。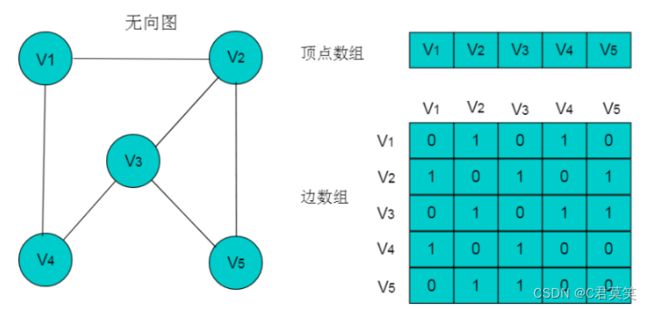
7.1 无向图的数组存储主要有以下特性
(1)顶点数组长度为图的顶点数目n。边数组为n X n的二维数组。
(2)边数组中,A[i][j] =1代表顶点i与顶点j邻接,A[i][j] = 0代表顶点i与顶点j不邻接。
(3)在无向图中。由于边是无向边,因此顶点的邻接关系是对称的,边数组为对称二维数组。
(4)顶点与自身之间并未邻接关系,因此边数组的对角线上的元素均为0。
(5)顶点的度即为顶点所在的行或者列1的数目。例如:顶点V2的度为3,则V2所在行和列中的1的数目为3。
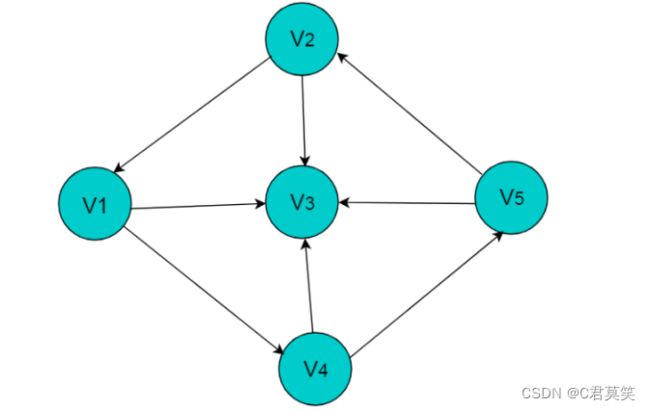
7.2 有向图的数组存储主要有以下特性
(1)顶点数组长度为图的顶点数目n。边数组为n X n的二维数组。
(2)边数组中,数组元素为1,即A[i][j] = 1,代表第i个顶点与第j个顶点邻接,且i为尾,j为头。 A[i][j] = 0代表顶点与顶点不邻接。
(3)在有向图中,由于边存在方向性,因此数组不一定为对称数组。
(4)对角线上元素为0。
(5)第i行中,1的数目代表第i个顶点的出度。例如:顶点V1的出度为2,则顶点V1所在行的1的数目为2。
(6)第j列中,1的数目代表第j个顶点的入度。例如:V3的入度为1,则V3所在列中1的数目为1。
7.3 数组存储方式优点
数组存储方式容易实现图的操作。例如:求某顶点的度、判断顶点之间是否有边(弧)、找顶点的邻接点等等。
7.4 数组存储方式缺点
采用数组存储方式,图若有n个顶点则需要n2个单元存储边(弧),空间存储效率为O(n2)。 当顶点数目较多,边数目较少时,此时图为稀疏图,这时尤其浪费空间。
例如:图中有 9 个顶点,边数为10,需要 9X9 的二维数组,而实际存储边信息空间只有10,造成空间浪费。

无向图的存储数组

8.邻接表存储
当使用数组存储时,主要有以下三个问题:
- 对于一个图,若图中的顶点数目过大,则无法使用邻接矩阵进行存储。因为在分配数组内存时可能会导致内存分配失败。
- 对于某些稀疏图(即顶点数目多,边数目少),创建的数组大小很大,而真正存储的有用信息又很少,这就造成了空间上的浪费。
- 有时两个点之间不止存在有一条边,这是用邻接矩阵就无法同时表示两条以上的边。
针对以上情况,提出了一种特殊的图存储方式,让每个节点拥有的数组大小刚好就等于它所连接的边数,由此建立一种邻接表的存储方式。
邻接表存储方法是一种数组存储和链式存储相结合的存储方法。在邻接表中,对图中的每个顶点建立一个单链表,第 i 个单链表中的结点依附于顶点 Vi 的边(对有向图是以顶点Vi为尾的弧)。链表中的节点称为表节点,共有 3个域,具体结构见下图:

表结点由三个域组成,adjvex存储与Vi邻接的点在图中的位置,nextarc存储下一条边或弧的结点,data存储与边或弧相关的信息如权值。
除表节点外,需要在数组中存储头节点,头结点由两个域组成,分别指向链表中第一个顶点和存储Vi的名或其他信息。具体结构如下图:

其中,data域中存储顶点相关信息,firstarc指向链表的第一个节点。
8.1 无向图采用邻接表方式存储
例如:无向图采用邻接表存储。

采用邻接表方式存储图,绘图过程中忽略边节点的info信息,头结点中的 data 域存储顶点名称。以V1顶点为例,V1顶点的邻接顶点为V2、V3、V4,则可以创建3个表节点,表节点中adjvex分别存储V2、V3、V4的索引1、2、3,按照此方式,得到的邻接表为:

无向图的邻接表存储特性
- 数组中头节点的数目为图的顶点数目。
- 链表的长度即为顶点的度。例如:V1顶点的度为3,则以V1为头节点的链表中表节点的数目为3。
8.2 有向图采用邻接表方式存储
例如:有向图采用邻接表存储。
采用邻接表方式存储图,绘图过程中忽略边节点的info信息,头结点中的data域存储顶点名称。以V1顶点为例,V1顶点的邻接顶点为V2、V3、V4,但是以V1顶点为尾的边只有两条,即和因此,创建2个表节点。表节点中adjvex分别存储V3、V4的索引2、3,按照此方式,得到的邻接表为:
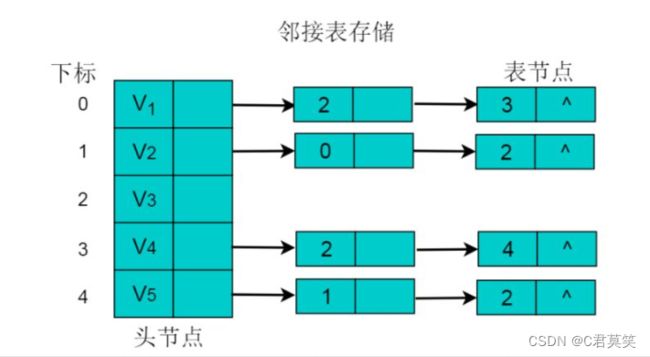
有向图的邻接表存储特性
- 数组中表节点的数目为图的顶点数目。
- 链表的长度即为顶点的出度。例如V1的出度为2,V1为头节点的链表中,表节点的数目为2。
- 顶点Vi的入度为邻接表中所有adjvex值域为i的表结点数目。例如:顶点V3的入度为4,则链表中所有adjvex值域为2的表结点数目为4。
注:图采用邻接表的方式表示时,其表示方式是不唯一的。这是因为在每个顶点对应的单链表中,各边节点的链接次序可以是任意的,取决于建立邻接表的算法以及边的输入次序。
总结
提起数据结构,大家最熟悉的恐怕就是数组、链表、二叉树。而对于“图”这种数据结构,很多人只停留在“听说过”阶段。但是,图是一种非常重要,而且跟现实息息相关的数据结构。比如,我们在使用百度、高德地图做导航的时候,城市的地图就是一种图结构;当我们用微信、QQ等社交软件的时候,我们的好友关系网也是一种图结构。