蓝桥杯第十三届决赛真题-左移右移
左移右移
- 一、思路分析
- 二、数组模拟双链表❗️❗️
- 三、代码展示
题目链接
问题描述
小蓝有一个长度为 N 的数组, 初始时从左到右依次是 1,2,3, …N 。
之后小蓝对这个数组进行了 M 次操作, 每次操作可能是以下 2 种之一:
左移 x, 即把 x 移动到最左边。
右移 x, 即把 x 移动到最右边。
请你回答经过 M 次操作之后, 数组从左到右每个数是多少?
输入格式
第一行包含 2 个整数, N 和 M。
以下 M 行每行一个操作, 其中 “L x "表示左移 x, "R x "表示右移 x 。
输出格式
输出 N 个数, 代表操作后的数组。
样例输入
5 3
L 3
L 2
R 1
样例输出
2 3 4 5 1
样例说明
样例中的数组变化如下:
[1,2,3,4,5]→[3,1,2,4,5]→[2,3,1,4,5]→[2,3,4,5,1]
评测用例规模与约定
对于50% 的评测用例, 1 ≤ N,M ≤ 10000.
对于 100% 的评测用例,1 ≤ N,M ≤ 200000,1 ≤ x ≤ N.
运行限制
最大运行时间:3s
最大运行内存: 512M
一、思路分析
首先最容易想的的办法就是创建一个数组,把1 - N的数字放进去,然后按照后面输入的字符(LR)和数字来操作:先找到数字,再挪动到头部或者尾部。
但是我们发现这种算法的时间复杂度是O(N ^ 2),而且这道题也会时间超时。那么下面就引入用数组模拟双链表的方法:
二、数组模拟双链表❗️❗️
在前面的文章我们讲过双向链表,用链表进行插入就可以不用挪动数据,但是我们发现查找数据还得遍历,那样又会变成O(N ^ 2),所以我们可以采用数组模拟。
先用一张图来演示:
假设我们要模拟这样一个链表:

现在我们用数组模拟就需要三个数组:一个是存放数值的数组,一个是记录节点左边位置的数组,一个是记录节点右边位置的数组。
int e[MAX];// 节点数据
int l[MAX];// 记录当前节点的左节点
int r[MAX];// 记录当前节点的右节点
int index;// 记录e下一个要插入的位置
我们让e的第0个位置代替head,第一个位置代替tail。
那么真实的结构是这样的:
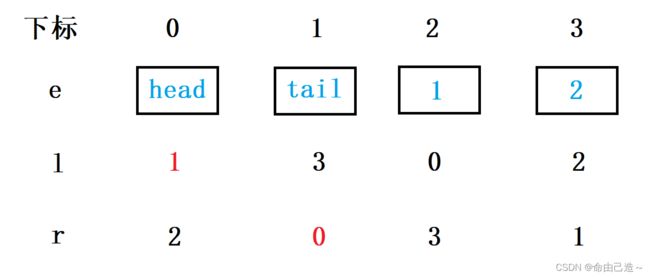
红的的数字就是我们首先要初始化的地方,也就是让我们找到头和尾。
而且index也需要初始化成2,因为0 和 1 的位置已经被占了,只能从下标2的位置开始插入。
构造函数:
mylist()
: index(2)
{
// 0位置表示头,1位置表示尾
l[1] = 0;
r[0] = 1;
}
在pos位置的右边插入数字:
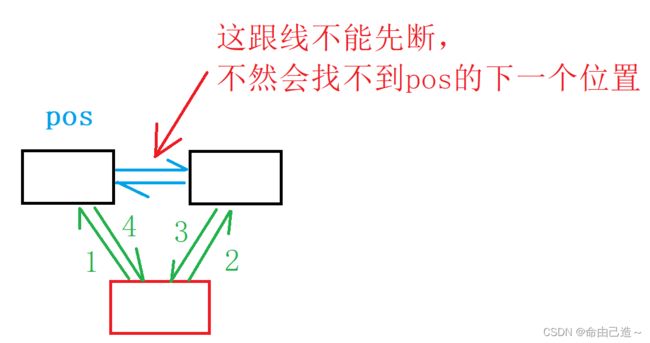
绿线表示链接的顺序,注意3和4的顺序不能变
// 在pos的右边插入
void insert(int pos, int x)
{
// 先插入到e中
e[index] = x;
// 四根线
l[index] = pos;
r[index] = r[pos];
l[r[pos]] = index;
r[pos] = index;
index++;
}
针对这道题目为了方便我们直接加一个尾插的成员函数:
void push_back(int x)
{
e[index] = x;
l[index] = l[1];
r[index] = 1;
r[l[1]] = index;
l[1] = index;
index++;
}
删除节点:
首先要知道并不是真的把当前位置清理,而是让pos位置的左右位置的 l 和 r 改变。我们就可以发现删除并不影响e数组中的数据相对位置
// 并不是真的删除
void pop(int pos)
{
// 左右互连
r[l[pos]] = r[pos];
l[r[pos]] = l[pos];
}
从左向右打印:
怎么找到head?
r[0]
void print()
{
for (int i = r[0]; i != 1; i = r[i])
{
cout << e[i] << " ";
}
cout << endl;
}
这道题我们还需要挪动数据,所以再写个成员函数:
// 将pos位置的数字挪到最左/右边
void move(char ch, int pos)
{
// 先删除pos位置(l和r)
pop(pos);
// 设置pos位置的l和r
if (ch == 'L')
{
l[pos] = 0;
r[pos] = r[0];
l[r[0]] = pos;
r[0] = pos;
}
else
{
l[pos] = l[1];
r[pos] = 1;
r[l[1]] = pos;
l[1] = pos;
}
}
通过这里我们就发现这道题用数组模拟链表的好处了:
比方说我们要找3,那么下标就是4,而且就算把3移动了,改变的也是 l 和 r 数组,不会影响e,再找下一个数字也可以这么找。
整个类的代码:
class mylist
{
public:
mylist()
: index(2)
{
// 0位置表示头,1位置表示尾
l[1] = 0;
r[0] = 1;
}
// 在pos的右边插入
void insert(int pos, int x)
{
// 先插入到e中
e[index] = x;
// 四根线
l[index] = pos;
r[index] = r[pos];
l[r[pos]] = index;
r[pos] = index;
index++;
}
void push_back(int x)
{
e[index] = x;
l[index] = l[1];
r[index] = 1;
r[l[1]] = index;
l[1] = index;
index++;
}
// 并不是真的删除
void pop(int pos)
{
// 左右互连
r[l[pos]] = r[pos];
l[r[pos]] = l[pos];
}
void print()
{
for (int i = r[0]; i != 1; i = r[i])
{
cout << e[i] << " ";
}
cout << endl;
}
// 将pos位置的数字挪到最左/右边
void move(char ch, int pos)
{
// 先删除pos位置(l和r)
pop(pos);
// 设置pos位置的l和r
if (ch == 'L')
{
l[pos] = 0;
r[pos] = r[0];
l[r[0]] = pos;
r[0] = pos;
}
else
{
l[pos] = l[1];
r[pos] = 1;
r[l[1]] = pos;
l[1] = pos;
}
}
private:
int e[MAX];// 节点数据
int l[MAX];// 记录当前节点的左节点
int r[MAX];// 记录当前节点的右节点
int index;// 记录e下一个要插入的位置
};
三、代码展示
#include