【路径规划】基于拓展随机树(RRT)算法的路径规划问题(Matlab代码实现)
欢迎来到本博客❤️❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
目录
1 概述
2 运行结果
3 参考文献
4 Matlab代码实现
1 概述
移动机器人路径规划[1] 是实现机器人自主导航的关键技术之一,其目的是使机器人在障碍物约束环境中,通过路径长度、搜索时间,平滑度以及避障能力等性能指标,求解出一条从起始点到目标点的最优或近似最优路径。
传统的移动机器人路径规划算法包括 dijkstra 算法、遗传算法、A∗算法[4]、粒子群算法等,然而面对复杂约束的机器人应用场景,这些算法往往需要大量的计算力。而Lavalle 提出的快速扩展随机树(Rapidly -Exploring RandomTree, RRT)算法,在状态空间中进行随机碰撞检测(Tree,RRT)算法,在状态空间中进行随机碰撞检测,将搜索空间逐渐扩展至可通行区域,进而搜索出一条从起始点到目标点的可行路径,避免了对规划空间建模,运行速度快,被广泛应用于移动机器人路径规划中。本文基于拓展随机树(RRT)算法的路径规划,用Matlab代码实现。
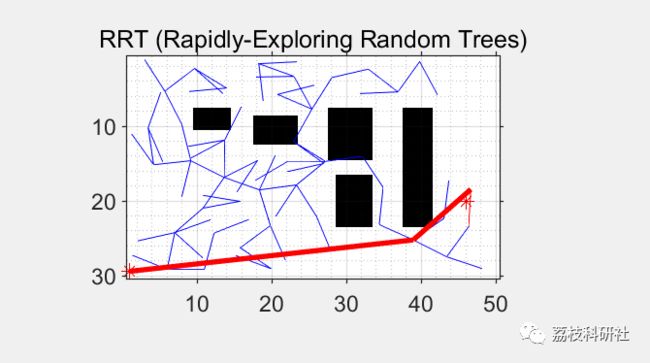
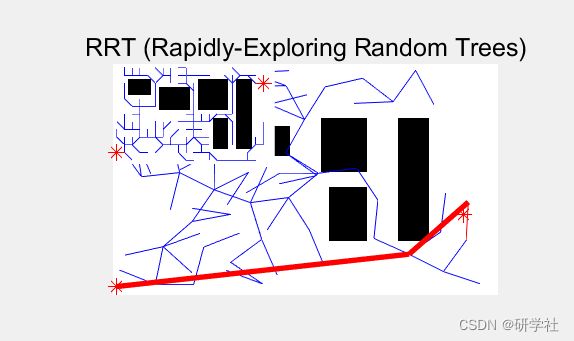
2 运行结果
RRT_Continous:
RRT_Discrete:
部分代码:
y = 5;
x = 12;
world_offset_x = 150/y;
world_offset_y = 250/y;
empty_world = ones(int32(world_offset_x),int32(world_offset_y));
% obstacle 1
for i = int32(world_offset_x*0.25):int32(world_offset_x*0.32)
for j = int32(world_offset_y*0.2):int32(world_offset_y*0.27)
empty_world(i,j) = 0;
end
end
% obstacle 2
for i = int32(world_offset_x*0.3):int32(world_offset_x*0.4)
for j = int32(world_offset_y*0.35):int32(world_offset_y*0.45)
empty_world(i,j) = 0;
end
end
% obstacle 3
for i = int32(world_offset_x*0.25):int32(world_offset_x*0.45)
for j = int32(world_offset_y*0.55):int32(world_offset_y*0.65)
empty_world(i,j) = 0;
end
end
% obstacle 4
for i = int32(world_offset_x*0.57):int32(world_offset_x*0.78)
for j = int32(world_offset_y*0.58):int32(world_offset_y*0.65)
empty_world(i,j) = 0;
end
end
% obstacle 5
for i = int32(world_offset_x*0.25):int32(world_offset_x*0.78)
for j = int32(world_offset_y*0.75):int32(world_offset_y*0.82)
empty_world(i,j) = 0;
end
end
save environment
imshow(empty_world)
axis on
grid on
grid minor
3 参考文献
[1]张志威,贾云伟,王永霞,付邦鹏.基于改进的快速扩展随机树的快速路径规划算法[J].天津理工大学学报,2022,38(03):14-19.
[2]侯宇翔,高焕兵,汪子健,杜传胜.改进RRT的移动机器人路径规划算法[J].电子测量技术,2022,45(16):47-52.DOI:10.19651/j.cnki.emt.2209355.