NLP-生成模型-2017-Transformer(二):Transformer各模块代码分析
一、WordEmbedding层模块(文本嵌入层)
Embedding Layer(文本嵌入层)的作用:无论是源文本嵌入还是目标文本嵌入,都是为了将文本中词汇的数字表示转变为向量表示, 由一维转为多维,希望在高维空间捕捉词汇间的关系.
- 文本中的单词在输入到文本嵌入层之前,已经通过word2index操作转换为数值【每个单词用该单词在所在词汇表中的序号表示】,将字符串形式的单词转为序号形式,然后输入到文本嵌入层。
- 再通过文本嵌入层将每个单词的一维的数值型序号转为多维向量。
import torch # 导入必备的工具包
import torch.nn as nn # 预定义的网络层torch.nn, 工具开发者已经帮助我们开发好的一些常用层【比如,卷积层, lstm层, embedding层等, 不需要我们再重新造轮子】
import math # 数学计算工具包
from torch.autograd import Variable # torch中变量封装函数Variable.
# 文本嵌入层:定义Embeddings类来实现文本嵌入层,这里s说明代表两个一模一样的嵌入层, 他们共享参数【该类继承nn.Module, 这样就有标准层的一些功能, 这里我们也可以理解为一种模式, 我们自己实现的所有层都会这样去写】
class Embeddings(nn.Module):
# 类的初始化函数, 有两个参数, 【vocab_word_tensor_input_size: 指词表的大小; word_embedding_size: 指转换后的词嵌入的维度】
def __init__(self, vocab_word_tensor_input_size, word_embedding_size):
super(Embeddings, self).__init__() # 使用super的方式指明继承nn.Module的初始化函数, 我们自己实现的所有层都会这样去写.
self.vocab_word_tensor_input_size = vocab_word_tensor_input_size
self.word_embedding_size = word_embedding_size
self.embedding = nn.Embedding(num_embeddings=vocab_word_tensor_input_size, embedding_dim=word_embedding_size) # 调用nn中的预定义层Embedding, 获得一个词嵌入对象self.embedding【vocab_word_tensor_input_size表示词汇表所有单词数量】
# 前向传播逻辑,所有层中都会有此函数,当传给该类的实例化对象参数时, 自动调用该类函数【参数word_tensor_input: 代表单词文本通过词汇映射(word2index)后的数值型张量,word_tensor_input里的每一个数字必须为0~vocab_word_tensor_input_size间的数来代表词汇表里的一个特定单词】
def forward(self, word_tensor_input):
# 将张量word_tensor_input传给self.embedding 返回词向量【math.sqrt(self.word_embedding_size)具有缩放的作用,控制转换后每一个元素的数值大小尽可能离散】
word_embedded = self.embedding(word_tensor_input) * math.sqrt(self.word_embedding_size)
return word_embedded
# 文本嵌入层测试
embedding01 = nn.Embedding(10, 6)
# 输入 word_tensor_input01 形状是 torch.Size([2, 4]),word_tensor_input01 中的每一个数字代表一个单词,该数字必须处于0~10, 通过embedding将每一个数字从一维转为三维
word_tensor_input01 = Variable(torch.LongTensor([[1, 2, 4, 5], [4, 3, 2, 9]])) # 其中所有元素的数值必须在0~10之间,1、2、4、5、4、3、2、9 代表在词汇表(该词汇表中的单词总数为10)中的序号分别为1、2、4、5、4、3、2、9的单词
word_embedded01 = embedding01(word_tensor_input01)
print("word_tensor_input01.shape = {0}\nword_tensor_input01 = {1}\nword_embedded01.shape = {2}\nword_embedded01 = {3}".format(word_tensor_input01.shape, word_tensor_input01, word_embedded01.shape, word_embedded01))
print("=" * 200)
# 输入 word_tensor_input02 形状是 torch.Size([2]),word_tensor_input02 中的每一个数字代表一个单词,该数字必须处于0~125, 通过embedding将每一个数字从一维转为四维
embedding02 = nn.Embedding(125, 5, padding_idx=0)
word_tensor_input02 = Variable(torch.LongTensor([99, 20])) # 其中所有元素的数值必须在0~125之间,99、20代表在词汇表(该词汇表中的单词总数为125)中的序号分别为99、20的单词
word_embedded02 = embedding02(word_tensor_input02)
print("word_tensor_input02.shape = {0}\nword_tensor_input02 = {1}\nword_embedded02.shape = {2}\nword_embedded02 = {3}".format(word_tensor_input02.shape, word_tensor_input02, word_embedded02.shape, word_embedded02))
print("=" * 200)
# 输入 word_tensor_input03 维度为 torch.Size([1]),word_tensor_input03 中的每一个数字代表一个单词,该数字必须处于0~21356, 通过embedding将每一个数字从一维转为七维
embedding03 = nn.Embedding(21356, 7, padding_idx=0)
word_tensor_input03 = Variable(torch.LongTensor([12929])) # 其中所有元素的数值必须在0~21356之间,12929代表在词汇表(该词汇表中的单词总数为21356)中的序号为12929的单词
word_embedded03 = embedding03(word_tensor_input03)
print("word_tensor_input03.shape = {0}\nword_tensor_input03 = {1}\nword_embedded03.shape = {2}\nword_embedded03 = {3}".format(word_tensor_input03.shape, word_tensor_input03, word_embedded03.shape, word_embedded03))
print("=" * 200)
打印结果:
word_tensor_input01.shape = torch.Size([2, 4])
word_tensor_input01 = tensor(
[
[1, 2, 4, 5],
[4, 3, 2, 9]
]
)
word_embedded01.shape = torch.Size([2, 4, 6])
word_embedded01 = tensor(
[
[[ 9.4595e-01, 1.3864e+00, 2.4944e-04, 7.7240e-01, 3.0468e+00, 1.4728e+00], [ 5.8059e-02, -1.4840e+00, -1.9020e+00, -9.9665e-01, -1.4388e-01, -1.3291e-01], [ 2.3830e+00, 1.2199e+00, -1.7175e+00, -2.2374e+00, -1.8652e+00, -1.1130e+00], [-2.7206e-01, 5.8435e-02, -5.0948e-01, -9.7521e-01, 5.1671e-02, 4.0077e-01]],
[[ 2.3830e+00, 1.2199e+00, -1.7175e+00, -2.2374e+00, -1.8652e+00, -1.1130e+00], [-9.6327e-01, -1.0315e+00, 9.8090e-01, 2.6795e+00, -3.1963e-01, -7.9420e-02], [ 5.8059e-02, -1.4840e+00, -1.9020e+00, -9.9665e-01, -1.4388e-01, -1.3291e-01], [ 1.4402e+00, 1.3477e+00, -3.0115e-01, 6.7661e-01, -9.7445e-01, 6.1007e-01]]
], grad_fn=<EmbeddingBackward>
)
========================================================================================================================================================================================================
word_tensor_input02.shape = torch.Size([2])
word_tensor_input02 = tensor([99, 20])
word_embedded02.shape = torch.Size([2, 5])
word_embedded02 = tensor([[-0.9370, -0.9051, 0.3929, 0.2125, 1.0556], [ 0.8013, 2.6944, 0.5470, 0.8228, 0.6134]], grad_fn=<EmbeddingBackward>)
========================================================================================================================================================================================================
word_tensor_input03.shape = torch.Size([1])
word_tensor_input03 = tensor([12929])
word_embedded03.shape = torch.Size([1, 7])
word_embedded03 = tensor([[ 1.1398, 1.3451, 1.6717, -2.6105, 2.3608, -0.3882, 0.0144]], grad_fn=<EmbeddingBackward>)
========================================================================================================================================================================================================
Process finished with exit code 0
二、位置编码器模块
在实验中尝试将position_embeddings这个向量注释掉,重新跑一遍生成模型,效果下降很明显,具体表现为容易生成重复的字/词。所以,这个位置编码相对于transformer来说是非常重要的。
1、位置编码器模块代码分析
import torch # 导入必备的工具包
import torch.nn as nn # 预定义的网络层torch.nn, 工具开发者已经帮助我们开发好的一些常用层【比如,卷积层, lstm层, embedding层等, 不需要我们再重新造轮子】
import math # 数学计算工具包
from torch.autograd import Variable # torch中变量封装函数Variable.
# 一、文本嵌入层:定义Embeddings类来实现文本嵌入层,这里s说明代表两个一模一样的嵌入层, 他们共享参数【该类继承nn.Module, 这样就有标准层的一些功能, 这里我们也可以理解为一种模式, 我们自己实现的所有层都会这样去写】
class Embeddings(nn.Module):
# 类的初始化函数, 有两个参数, 【vocab_word_tensor_input_size: 指词表的大小; word_embedding_size: 指转换后的词嵌入的维度】
def __init__(self, vocab_word_tensor_input_size, word_embedding_size):
super(Embeddings, self).__init__() # 使用super的方式指明继承nn.Module的初始化函数, 我们自己实现的所有层都会这样去写.
self.vocab_word_tensor_input_size = vocab_word_tensor_input_size
self.word_embedding_size = word_embedding_size
self.embedding = nn.Embedding(num_embeddings=vocab_word_tensor_input_size, word_embedding_size=word_embedding_size) # 调用nn中的预定义层Embedding, 获得一个词嵌入对象self.embedding【vocab_word_tensor_input_size表示词汇表所有单词数量】
# 前向传播逻辑,所有层中都会有此函数,当传给该类的实例化对象参数时, 自动调用该类函数【参数word_tensor_input: 代表单词文本通过词汇映射(word2index)后的数值型张量,word_tensor_input里的每一个数字必须为0~vocab_word_tensor_input_size间的数来代表词汇表里的一个特定单词】
def forward(self, word_tensor_input):
# 将张量word_tensor_input传给self.embedding 返回词向量【math.sqrt(self.word_embedding_size)具有缩放的作用,控制转换后每一个元素的数值大小尽可能离散】
word_embedded = self.embedding(word_tensor_input) * math.sqrt(self.word_embedding_size)
return word_embedded
# 二、位置编码器:我们同样把它看做一个层, 因此会继承nn.Module
class PositionalEncoding(nn.Module):
def __init__(self, word_embedding_size, dropout, max_len=20): # 位置编码器类的初始化函数【共有三个参数, word_embedding_size: 词嵌入维度; dropout: 置0比率; max_len: 每个句子的最大长度】
super(PositionalEncoding, self).__init__()
print("word_embedding_size = ", word_embedding_size, "---max_len = ", max_len)
self.dropout = nn.Dropout(p=dropout) # 实例化nn中预定义的Dropout层, 并将dropout传入其中, 获得对象self.dropout
# 初始化一个形状为(max_len * word_embedding_size)的位置编码矩阵【行大小max_len代表句子长度,每一行代表一个单词;列大小word_embedding_size代表词向量维度】
PE = torch.zeros(max_len, word_embedding_size)
# 初始化一个形状为(max_len*1)绝对位置矩阵,在这里,词汇的绝对位置就是用该词汇在该句子中的索引表示
# 所以我们首先使用arange方法获得一个连续自然数向量,然后再使用unsqueeze方法拓展向量维度使其成为矩阵,
# 又因为参数传的是1,代表矩阵拓展的位置,会使向量变成一个max_len x 1 的矩阵,
position = torch.arange(0, max_len).unsqueeze(1)
print("position.shape = {0}\nposition = \n{1}".format(position.shape, position)) # torch.Size([10, 1])
# 绝对位置矩阵position初始化之后,接下来就是考虑如何将这些位置信息加入到位置编码矩阵中
# 最简单的思路就是:将 torch.Size([max_len, 1]) 的绝对位置矩阵position变换成 torch.Size([max_len, word_embedding_size]) 形状,然后覆盖原来的初始化的位置编码矩阵pe即可。
# 要想将torch.Size([max_len, 1]) 的绝对位置矩阵position变换成 torch.Size([max_len, word_embedding_size]) 形状,需要一个形状为 torch.Size([1, word_embedding_size])的变化矩阵【用div_term表示】
# 对变化矩阵div_term的要求:
# 1、形状为torch.Size([1, word_embedding_size])
# 2、能够将自然数的绝对位置编码缩放成足够小的数字,有利于在之后的梯度下降过程中更快的收敛
# 使用arange获得一个自然数矩阵a,并没有按照预计的一样初始化一个形状为 torch.Size([1, word_embedding_size])的矩阵,而是有一个跳跃,只初始化一半,即初始化一个形状为torch.Size([1, word_embedding_size/2])的矩阵
# 我们可以把它看作是初始化了两次,而每次初始化的变换矩阵会做不同的处理,第一次初始化的变换矩阵分布在正弦波上, 第二次初始化的变换矩阵分布在余弦波上,
# 并把这两个矩阵分别填充在位置编码矩阵的偶数和奇数位置上,组成最终的位置编码矩阵.
a = torch.arange(0, word_embedding_size, 2)
b = -(math.log(10000.0) / word_embedding_size) # 对a进行缩放的比例
print("a = {0}----b = {1}".format(a, b)) # a = tensor([0, 2, 4]), b = -1.5350567286626973
div_term = torch.exp(a * b) # 定义(1*word_embedding_size/2)形状的变换矩阵div_term【跳跃式初始化】
print("div_term.shape = {0}\ndiv_term = = torch.exp(a * b) = {1}".format(div_term.shape, div_term)) # div_term.shape = torch.Size([3]),div_term = tensor([1.0000, 0.0464, 0.0022])
position_div_term = position * div_term # torch.Size([10, 1]) × torch.Size([3]) >>> torch.Size([10, 3])
print("position_div_term.shape = {0}\nposition_div_term = \n{1}".format(position_div_term.shape, position_div_term)) # torch.Size([10, 3])
position_div_term_sin = torch.sin(position_div_term)
position_div_term_cos = torch.cos(position_div_term)
print("position_div_term_sin.shape = {0}\nposition_div_term_sin = \n{1}".format(position_div_term_sin.shape, position_div_term_sin))
print("position_div_term_cos.shape = {0}\nposition_div_term_cos = \n{1}".format(position_div_term_cos.shape, position_div_term_cos))
PE[:, 0::2] = position_div_term_sin # 把绝对位置矩阵position经过变换矩阵div_term转换后的矩阵,再经sin()函数处理,填充在位置编码矩阵pe的偶数列
PE[:, 1::2] = position_div_term_cos # 把绝对位置矩阵position经过变换矩阵div_term转换后的矩阵,再经cos()函数处理,填充在位置编码矩阵pe的奇数列
PE = PE.unsqueeze(0) # 将二维矩阵pe拓展为三维,用于和embedding层的输出(一个三维张量)相加,
print("初始化的位置编码:PE.shape = {0}\nPE = \n{1}".format(PE.shape, PE))
self.register_buffer('PE', PE) # 把pe位置编码矩阵注册成模型的buffer【buffer是对模型效果有帮助的,但是却不是模型结构中超参数或者参数,不需要随着优化步骤进行更新的增益对象。注册之后我们就可以在模型保存后重加载时和模型结构与参数一同被加载】
def forward(self, word_embedded): # 参数word_embedded: 表示文本序列的词嵌入表示
print("=" * 50, "进入forward阶段", "=" * 50)
PE = self.PE[:, :word_embedded.size(1)] # 对pe做一些适配工作, 将这个三维张量的第二维也就是句子最大长度的那一维将切片到与输入的word_embedded的第二维相同即word_embedded.size(1),使pe与word_embedded的样式相同【因为我们默认max_len为5000一般来讲实在太大了,很难有一条句子包含5000个词汇,所以要进行与输入张量的适配】
print("根据当前句子长度截断后位置编码:PE.shape = {0}\nPE = \n{1}".format(PE.shape, PE))
print("word_embedded.shape = {0}----word_embedded = \n{1}".format(word_embedded.shape, word_embedded))
word_embedded_plus_pe = word_embedded + Variable(PE, requires_grad=False) # 将pe使用Variable进行封装,但是它是不需要进行梯度求解的,因此把requires_grad设置成false.
print("当前批次所有句子embedding后+位置编码:word_embedded_plus_pe.shape = {0}\nword_embedded_plus_pe = \n{1}".format(word_embedded_plus_pe.shape, word_embedded_plus_pe))
word_embedded_plus_pe_dropout = self.dropout(word_embedded_plus_pe) # 最后使用self.dropout对象进行'丢弃'操作
print("word_embedded_plus_pe_dropout.shape = {0}\nword_embedded_plus_pe_dropout = \n{1}".format(word_embedded_plus_pe_dropout.shape, word_embedded_plus_pe_dropout))
return word_embedded_plus_pe_dropout
if __name__ == "__main__":
dropout = 0.1 # 置0比率为0.1
max_len = 10 # 句子最大长度
# 实例化Embedding层
embedding01 = nn.Embedding(10, 6)
# 输入 word_tensor_input01 形状是 torch.Size([2, 4]),word_tensor_input01 中的每一个数字代表一个单词,该数字必须处于0~10, 通过embedding将每一个数字从一维转为三维
word_tensor_input01 = Variable(torch.LongTensor([[1, 2, 4, 5], [4, 3, 2, 9]])) # 其中所有元素的数值必须在0~10之间,1、2、4、5、4、3、2、9 代表在词汇表(该词汇表中的单词总数为10)中的序号分别为1、2、4、5、4、3、2、9的单词
word_embedded01 = embedding01(word_tensor_input01)
# 实例化PositionalEncoding层
PE = PositionalEncoding(word_embedding_size=word_embedded01.size(2), dropout=dropout, max_len=max_len)
PE_result = PE(word_embedded01)
print("PE_result.shape = {0} \nPE_result = \n{1}".format(PE_result.shape, PE_result))
print("=" * 200)
打印结果:
word_embedding_size = 6 ---max_len = 10
position.shape = torch.Size([10, 1])
position =
tensor([[0],
[1],
[2],
[3],
[4],
[5],
[6],
[7],
[8],
[9]])
a = tensor([0, 2, 4])----b = -1.5350567286626973
div_term.shape = torch.Size([3])
div_term = = torch.exp(a * b) = tensor([1.0000, 0.0464, 0.0022])
position_div_term.shape = torch.Size([10, 3])
position_div_term =
tensor([[0.0000e+00, 0.0000e+00, 0.0000e+00],
[1.0000e+00, 4.6416e-02, 2.1544e-03],
[2.0000e+00, 9.2832e-02, 4.3089e-03],
[3.0000e+00, 1.3925e-01, 6.4633e-03],
[4.0000e+00, 1.8566e-01, 8.6177e-03],
[5.0000e+00, 2.3208e-01, 1.0772e-02],
[6.0000e+00, 2.7850e-01, 1.2927e-02],
[7.0000e+00, 3.2491e-01, 1.5081e-02],
[8.0000e+00, 3.7133e-01, 1.7235e-02],
[9.0000e+00, 4.1774e-01, 1.9390e-02]])
position_div_term_sin.shape = torch.Size([10, 3])
position_div_term_sin =
tensor([[ 0.0000, 0.0000, 0.0000],
[ 0.8415, 0.0464, 0.0022],
[ 0.9093, 0.0927, 0.0043],
[ 0.1411, 0.1388, 0.0065],
[-0.7568, 0.1846, 0.0086],
[-0.9589, 0.2300, 0.0108],
[-0.2794, 0.2749, 0.0129],
[ 0.6570, 0.3192, 0.0151],
[ 0.9894, 0.3629, 0.0172],
[ 0.4121, 0.4057, 0.0194]])
position_div_term_cos.shape = torch.Size([10, 3])
position_div_term_cos =
tensor([[ 1.0000, 1.0000, 1.0000],
[ 0.5403, 0.9989, 1.0000],
[-0.4161, 0.9957, 1.0000],
[-0.9900, 0.9903, 1.0000],
[-0.6536, 0.9828, 1.0000],
[ 0.2837, 0.9732, 0.9999],
[ 0.9602, 0.9615, 0.9999],
[ 0.7539, 0.9477, 0.9999],
[-0.1455, 0.9318, 0.9999],
[-0.9111, 0.9140, 0.9998]])
初始化的位置编码:PE.shape = torch.Size([1, 10, 6])
PE =
tensor([[[ 0.0000, 1.0000, 0.0000, 1.0000, 0.0000, 1.0000],
[ 0.8415, 0.5403, 0.0464, 0.9989, 0.0022, 1.0000],
[ 0.9093, -0.4161, 0.0927, 0.9957, 0.0043, 1.0000],
[ 0.1411, -0.9900, 0.1388, 0.9903, 0.0065, 1.0000],
[-0.7568, -0.6536, 0.1846, 0.9828, 0.0086, 1.0000],
[-0.9589, 0.2837, 0.2300, 0.9732, 0.0108, 0.9999],
[-0.2794, 0.9602, 0.2749, 0.9615, 0.0129, 0.9999],
[ 0.6570, 0.7539, 0.3192, 0.9477, 0.0151, 0.9999],
[ 0.9894, -0.1455, 0.3629, 0.9318, 0.0172, 0.9999],
[ 0.4121, -0.9111, 0.4057, 0.9140, 0.0194, 0.9998]]])
================================================== 进入forward阶段 ==================================================
根据当前句子长度截断后位置编码:PE.shape = torch.Size([1, 4, 6])
PE =
tensor([[[ 0.0000, 1.0000, 0.0000, 1.0000, 0.0000, 1.0000],
[ 0.8415, 0.5403, 0.0464, 0.9989, 0.0022, 1.0000],
[ 0.9093, -0.4161, 0.0927, 0.9957, 0.0043, 1.0000],
[ 0.1411, -0.9900, 0.1388, 0.9903, 0.0065, 1.0000]]])
word_embedded.shape = torch.Size([2, 4, 6])----word_embedded =
tensor([[[ 0.2816, 0.7202, -0.0137, 0.1765, -0.7214, -0.1437],
[-0.5911, 0.4584, 0.2886, 0.6425, 0.1670, -0.2737],
[-2.0529, -1.1460, -1.3096, -0.2932, -0.0770, -0.4256],
[ 0.2311, -0.4507, 0.4163, 0.0599, 1.0705, -0.3261]],
[[-2.0529, -1.1460, -1.3096, -0.2932, -0.0770, -0.4256],
[ 0.2528, 1.7542, 0.2814, 0.3276, -0.5405, 0.1219],
[-0.5911, 0.4584, 0.2886, 0.6425, 0.1670, -0.2737],
[-0.4525, 0.4749, -0.2352, -0.7722, 1.2100, 2.1487]]],
grad_fn=<EmbeddingBackward>)
当前批次所有句子embedding后+位置编码:word_embedded_plus_pe.shape = torch.Size([2, 4, 6])
word_embedded_plus_pe =
tensor([[[ 0.2816, 1.7202, -0.0137, 1.1765, -0.7214, 0.8563],
[ 0.2504, 0.9987, 0.3350, 1.6414, 0.1691, 0.7263],
[-1.1436, -1.5621, -1.2169, 0.7025, -0.0727, 0.5744],
[ 0.3722, -1.4407, 0.5550, 1.0502, 1.0770, 0.6738]],
[[-2.0529, -0.1460, -1.3096, 0.7068, -0.0770, 0.5744],
[ 1.0942, 2.2945, 0.3278, 1.3266, -0.5383, 1.1219],
[ 0.3182, 0.0423, 0.3813, 1.6382, 0.1713, 0.7263],
[-0.3114, -0.5151, -0.0964, 0.2181, 1.2165, 3.1487]]],
grad_fn=<AddBackward0>)
word_embedded_plus_pe_dropout.shape = torch.Size([2, 4, 6])
word_embedded_plus_pe_dropout =
tensor([[[ 0.3129, 1.9113, -0.0152, 1.3073, -0.8015, 0.9514],
[ 0.2782, 1.1097, 0.3723, 1.8238, 0.1879, 0.8070],
[-1.2706, -1.7357, -1.3521, 0.7805, -0.0807, 0.6382],
[ 0.4136, -1.6008, 0.6167, 1.1669, 1.1967, 0.7487]],
[[-2.2810, -0.1622, -1.4551, 0.7853, -0.0855, 0.6382],
[ 0.0000, 2.5495, 0.3642, 1.4740, -0.0000, 1.2465],
[ 0.3536, 0.0470, 0.4237, 1.8202, 0.1903, 0.8070],
[-0.3460, -0.5723, -0.0000, 0.2424, 1.3517, 3.4985]]],
grad_fn=<MulBackward0>)
PE_result.shape = torch.Size([2, 4, 6])
PE_result =
tensor([[[ 0.3129, 1.9113, -0.0152, 1.3073, -0.8015, 0.9514],
[ 0.2782, 1.1097, 0.3723, 1.8238, 0.1879, 0.8070],
[-1.2706, -1.7357, -1.3521, 0.7805, -0.0807, 0.6382],
[ 0.4136, -1.6008, 0.6167, 1.1669, 1.1967, 0.7487]],
[[-2.2810, -0.1622, -1.4551, 0.7853, -0.0855, 0.6382],
[ 0.0000, 2.5495, 0.3642, 1.4740, -0.0000, 1.2465],
[ 0.3536, 0.0470, 0.4237, 1.8202, 0.1903, 0.8070],
[-0.3460, -0.5723, -0.0000, 0.2424, 1.3517, 3.4985]]],
grad_fn=<MulBackward0>)
========================================================================================================================================================================================================
Process finished with exit code 0
2、绘制词汇向量中特征的分布曲线
import numpy as np
import torch # 导入必备的工具包
import torch.nn as nn # 预定义的网络层torch.nn, 工具开发者已经帮助我们开发好的一些常用层【比如,卷积层, lstm层, embedding层等, 不需要我们再重新造轮子】
import math # 数学计算工具包
from torch.autograd import Variable # torch中变量封装函数Variable.
import matplotlib.pyplot as plt
# 位置编码器:我们同样把它看做一个层, 因此会继承nn.Module
class PositionalEncoding(nn.Module):
def __init__(self, word_embedding_size, dropout, max_len=5000): # 位置编码器类的初始化函数【共有三个参数, word_embedding_size: 词嵌入维度; dropout: 置0比率; max_len: 每个句子的最大长度】
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout) # 实例化nn中预定义的Dropout层, 并将dropout传入其中, 获得对象self.dropout
pe = torch.zeros(max_len, word_embedding_size) # 初始化一个形状为(max_len * word_embedding_size)的位置编码矩阵【行大小max_len代表句子长度,每一行代表一个单词;列大小word_embedding_size代表词向量维度】
position = torch.arange(0, max_len).unsqueeze(1) # 初始化一个形状为(max_len*1)绝对位置矩阵
div_term = torch.exp(torch.arange(0, word_embedding_size, 2) * -(math.log(10000.0) / word_embedding_size)) # 定义(1*word_embedding_size/2)形状的变换矩阵div_term【跳跃式初始化】
pe[:, 0::2] = torch.sin(position * div_term) # 把绝对位置矩阵position经过变换矩阵div_term转换后的矩阵,再经sin()函数处理,填充在位置编码矩阵pe的偶数列
pe[:, 1::2] = torch.cos(position * div_term) # 把绝对位置矩阵position经过变换矩阵div_term转换后的矩阵,再经cos()函数处理,填充在位置编码矩阵pe的奇数列
pe = pe.unsqueeze(0) # 将二维矩阵pe拓展为三维,用于和embedding层的输出(一个三维张量)相加,
self.register_buffer('pe', pe) # 把pe位置编码矩阵注册成模型的buffer【buffer是对模型效果有帮助的,但是却不是模型结构中超参数或者参数,不需要随着优化步骤进行更新的增益对象。注册之后我们就可以在模型保存后重加载时和模型结构与参数一同被加载】
def forward(self, word_embedded): # 参数word_embedded: 表示文本序列的词嵌入表示
pe = self.pe[:, :word_embedded.size(1)] # 对pe做一些适配工作, 将这个三维张量的第二维也就是句子最大长度的那一维将切片到与输入的word_embedded的第二维相同即word_embedded.size(1),使pe与word_embedded的样式相同【因为我们默认max_len为5000一般来讲实在太大了,很难有一条句子包含5000个词汇,所以要进行与输入张量的适配】
print("word_embedded.shape = {0}\nword_embedded = {1}".format(word_embedded.shape, word_embedded))
print("pe.shape = {0}\npe = {1}".format(pe.shape, pe))
word_embedded = word_embedded + Variable(pe, requires_grad=False) # 将pe使用Variable进行封装,但是它是不需要进行梯度求解的,因此把requires_grad设置成false.
return self.dropout(word_embedded) # 最后使用self.dropout对象进行'丢弃'操作, 并返回结果.
if __name__ == "__main__":
# 绘制词汇向量中特征的分布曲线
plt.figure(figsize=(15, 5)) # 创建一张15 x 5大小的画布
pe = PositionalEncoding(word_embedding_size=20, dropout=0) # 实例化PositionalEncoding类得到pe对象, 输入参数是20和0
y = pe(Variable(torch.zeros(1, 100, 20))) # 然后向pe传入被Variable封装的tensor, 这样pe会直接执行forward函数,且这个tensor里的数值都是0, 被处理后相当于位置编码张量
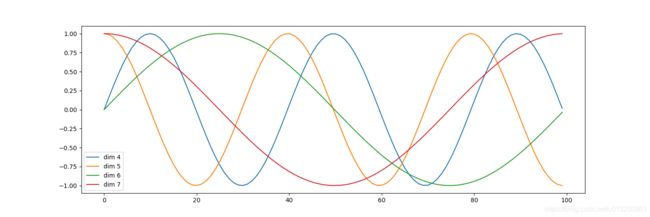
plt.plot(np.arange(100), y[0, :, 4:8].data.numpy()) # 然后定义画布的横纵坐标, 横坐标到100的长度, 纵坐标是某一个词汇中的某维特征在不同长度下对应的值【因为总共有20维之多, 我们这里只查看4,5,6,7维的值.】
plt.legend(["dim %d" % p for p in [4, 5, 6, 7]]) # 在画布上填写维度提示信息
plt.savefig("./transformer_pe.png") # 保存图像
打印结果:
word_embedded.shape = torch.Size([1, 100, 20])
word_embedded = tensor([[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]])
pe.shape = torch.Size([1, 100, 20])
pe = tensor([[[ 0.0000e+00, 1.0000e+00, 0.0000e+00, ..., 1.0000e+00,
0.0000e+00, 1.0000e+00],
[ 8.4147e-01, 5.4030e-01, 3.8767e-01, ..., 1.0000e+00,
2.5119e-04, 1.0000e+00],
[ 9.0930e-01, -4.1615e-01, 7.1471e-01, ..., 1.0000e+00,
5.0238e-04, 1.0000e+00],
...,
[ 3.7961e-01, -9.2515e-01, 7.9395e-01, ..., 9.9813e-01,
2.4363e-02, 9.9970e-01],
[-5.7338e-01, -8.1929e-01, 9.6756e-01, ..., 9.9809e-01,
2.4614e-02, 9.9970e-01],
[-9.9921e-01, 3.9821e-02, 9.8984e-01, ..., 9.9805e-01,
2.4865e-02, 9.9969e-01]]])
- 每条颜色的曲线代表某一个词汇中的特征在不同位置的含义.
- 保证同一词汇随着所在位置不同它对应位置嵌入向量会发生变化.
- 正弦波和余弦波的值域范围都是1到-1这又很好的控制了嵌入数值的大小, 有助于梯度的快速计算.
三、自注意力机制 +【Padding Mask、Sequence Mask】
self-attention中,Q和K在点积之后,需要先经过mask再进行softmax,因此,对于要屏蔽的部分,mask之后的输出需要为负无穷,这样softmax之后输出才为0。
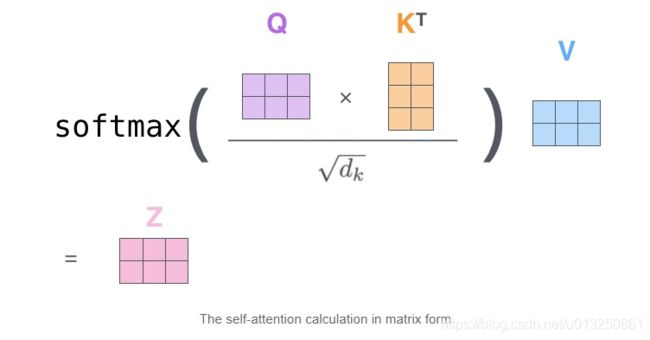
# 注意力机制的实现【输入分别是query, key, value, mask(掩码张量), dropout是nn.Dropout层的实例化对象, 默认为None】
def attention(query, key, value, mask=None, dropout=None):
d_k = query.size(-1) # 在函数中, 首先取query的最后一维的大小, 一般情况下就等同于词嵌入维度, 命名为d_k
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k) # torch.matmul()函数只对2个矩阵的最后两维度的数据进行操作。按照注意力公式, 将query(2*3*4*2)与”key的转置“(2*3*2*4)相乘【query、key最后一维一般都是词向量维度】, 这里面key是将最后两个维度进行转置, 再除以缩放系数根号下d_k, 得到注意力得分张量scores【这种计算方法也称为缩放点积注意力计算】
# print("attention---->scores.shape = {0}".format(scores.shape)) # torch.Size([2, 3, 4, 4])
# 接着判断是否使用掩码张量
if mask is not None:
# print("attention---->mask.shape = {0}".format(mask.shape)) # torch.Size([1, 3, 4, 4])
scores = scores.masked_fill(mask == 0, -1e9) # 使用tensor的masked_fill方法, 将掩码张量和scores张量每个位置一一比较, 如果掩码张量处为0, 则对应的scores张量用一个非常小的数值(比如:-1e9)替换【mask的shape必须与scores的shape相同或可传播/broadcasting-semantics】
attention_weight = F.softmax(scores, dim=-1) # 对scores的最后一维进行softmax操作, 使用F.softmax方法, 第一个参数是softmax对象, 第二个是目标维度. 这样获得最终的注意力张量
if dropout is not None: # 之后判断是否使用dropout进行随机置0
attention_weight = dropout(attention_weight) # 将p_attn传入dropout对象中进行'丢弃'处理
# print("attention---->attention_weight.shape = {0}".format(attention_weight.shape)) # torch.Size([2, 3, 4, 4])
attention_result = torch.matmul(attention_weight, value) # 根据公式将attention_weight(2*3*4*4)与value(2*3*4*2)张量相乘获得最终的query注意力表示
# print("attention---->attention_result.shape = {0}".format(attention_result.shape)) # torch.Size([2, 3, 4, 2])
return attention_weight, attention_result # 返回注意力权重、最终的query注意力表示
1、Padding Mask(Encoder、Decoder的Self-Attention中都需要Padding Mask)
Transformer 的 Encoder、Decoder中的 Self-Attention 都需要忽略 padding 部分的影响
2、Subsequent Mask(Decoder的Self-Attention中需要Subsequent Mask)
在语言模型中,常常需要从上一个词预测下一个词,但如果要在LM中应用 self attention 或者是同时使用上下文的信息,要想不泄露要预测的标签信息,就需要 mask 来“遮盖”它。
Transformer 是包括 Encoder和 Decoder的,
- Encoder中 self-attention 只需要 padding mask,
- Decoder 不仅需要 padding mask,还需要防止标签泄露,即在 t 时刻不能看到 t 时刻之后的信息,因此在上述 padding mask的基础上,还要加上 Subsequent mask。
Subsequent mask 一般是通过生成一个上三角为0的矩阵来实现的,上三角区域对应要mask的部分。
在Transformer 的 Decoder中,先不考虑 padding mask,一个包括四个词的句子[A,B,C,D]在计算了相似度scores之后,得到下面第一幅图,将scores的上三角区域mask掉,即替换为负无穷,再做softmax得到第三幅图。这样,比如输入 B 在self-attention之后,也只和A,B有关,而与后序信息无关。
因为在softmax之后的加权平均中: B’ = 0.48A+0.52B,而 C,D 对 B’不做贡献。

实际应用中,Decoder 需要结合 padding mask 和 Subsequent mask。
3、Transformer 中 的两种 Mask【Padding Mask、Sequence Mask】
import torch
def padding_mask(sentence, pad_idx):
mask = (sentence != pad_idx).int().unsqueeze(-2) # [B, 1, L]
return mask
def subsequent_mask(sentence):
batch_size, seq_len = sentence.size()
mask = 1 - torch.triu(torch.ones((seq_len, seq_len), dtype=torch.uint8), diagonal=1)
mask = mask.unsqueeze(0).expand(batch_size, -1, -1) # [B, L, L]
return mask
def test():
# 以最简化的形式测试Transformer的两种mask
sentence = torch.LongTensor([[1, 2, 5, 8, 3, 0]]) # batch_size=1, seq_len=3,padding_idx=0
embedding = torch.nn.Embedding(num_embeddings=50000, embedding_dim=300, padding_idx=0)
query = embedding(sentence)
key = embedding(sentence)
scores = torch.matmul(query, key.transpose(-2, -1))
print("\nscores = \n", scores)
mask_p = padding_mask(sentence, 0)
mask_s = subsequent_mask(sentence)
print("mask_p = \n", mask_p)
print("mask_s = \n", mask_s)
mask_encoder = mask_p
mask_decoder = mask_p & mask_s # 结合 padding mask 和 Subsequent mask
print("mask_encoder = \n", mask_encoder)
print("mask_decoder = \n", mask_decoder)
scores_encoder = scores.masked_fill(mask_encoder == 0, -1e9) # 对于scores,在mask==0的位置填充-1e9
scores_decoder = scores.masked_fill(mask_decoder == 0, -1e9) # 对于scores,在mask==0的位置填充-1e9
print("scores_encoder = \n", scores_encoder)
print("scores_decoder = \n", scores_decoder)
test()
打印结果:
scores =
tensor([[[256.9339, -4.1667, 21.3342, -9.0958, 2.4808, 0.0000],
[ -4.1667, 285.8431, -20.5250, -10.3684, 18.9549, 0.0000],
[ 21.3342, -20.5250, 291.5568, 18.6109, 15.0059, 0.0000],
[ -9.0958, -10.3684, 18.6109, 279.6891, -20.5765, 0.0000],
[ 2.4808, 18.9549, 15.0059, -20.5765, 287.6636, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]],
grad_fn=<UnsafeViewBackward>)
mask_p =
tensor([[[1, 1, 1, 1, 1, 0]]], dtype=torch.int32)
mask_s =
tensor([[[1, 0, 0, 0, 0, 0],
[1, 1, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 0],
[1, 1, 1, 1, 0, 0],
[1, 1, 1, 1, 1, 0],
[1, 1, 1, 1, 1, 1]]], dtype=torch.uint8)
mask_encoder =
tensor([[[1, 1, 1, 1, 1, 0]]], dtype=torch.int32)
mask_decoder =
tensor([[[1, 0, 0, 0, 0, 0],
[1, 1, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 0],
[1, 1, 1, 1, 0, 0],
[1, 1, 1, 1, 1, 0],
[1, 1, 1, 1, 1, 0]]], dtype=torch.int32)
scores_encoder =
tensor([[[ 2.5693e+02, -4.1667e+00, 2.1334e+01, -9.0958e+00, 2.4808e+00, -1.0000e+09],
[-4.1667e+00, 2.8584e+02, -2.0525e+01, -1.0368e+01, 1.8955e+01, -1.0000e+09],
[ 2.1334e+01, -2.0525e+01, 2.9156e+02, 1.8611e+01, 1.5006e+01, -1.0000e+09],
[-9.0958e+00, -1.0368e+01, 1.8611e+01, 2.7969e+02, -2.0577e+01, -1.0000e+09],
[ 2.4808e+00, 1.8955e+01, 1.5006e+01, -2.0577e+01, 2.8766e+02, -1.0000e+09],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, -1.0000e+09]]],
grad_fn=<MaskedFillBackward0>)
scores_decoder =
tensor([[[ 2.5693e+02, -1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-4.1667e+00, 2.8584e+02, -1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[ 2.1334e+01, -2.0525e+01, 2.9156e+02, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-9.0958e+00, -1.0368e+01, 1.8611e+01, 2.7969e+02, -1.0000e+09, -1.0000e+09],
[ 2.4808e+00, 1.8955e+01, 1.5006e+01, -2.0577e+01, 2.8766e+02, -1.0000e+09],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, -1.0000e+09]]],
grad_fn=<MaskedFillBackward0>)
============================== 1 passed in 0.80s ==============================
Process finished with exit code 0
可以看到
- mask_decoder 的第6列为0 ,对应padding mask,
- mask_decoder上三角为0,对应Subsequent mask。
对于Decoder,在batch训练时会同时需要padding mask和Subsequent mask。
在测试时为单例,仅需要加上Subsequent mask,这样可以固定住每一步生成的词,让前面生成的词在self-attention时不会包含后面词的信息,这样也使测试和训练保持了一致。
不过,在测试过程中,预测生成的句子长度逐步增加,因此每一步都会要生成新的Subsequent mask矩阵的,是维度逐步增加的下三角方阵。
4、测试注意力机制 + Subsequent Mask
import numpy as np
import torch # 导入必备的工具包
import torch.nn as nn # 预定义的网络层torch.nn, 工具开发者已经帮助我们开发好的一些常用层【比如,卷积层, lstm层, embedding层等, 不需要我们再重新造轮子】
import math # 数学计算工具包
import torch.nn.functional as F # 工具包装载了网络层中那些只进行计算, 而没有参数的层
from torch.autograd import Variable # torch中变量封装函数Variable.
import matplotlib.pyplot as plt
import copy # 用于深度拷贝的copy工具包
import time
EMBEDDING_DIM = 6 # 词嵌入维度的大小
DROPOUT = 0.1 # dropout本身是对模型结构中的节点数进行随机抑制的比率,又因为节点被抑制等效就是该节点的输出都是0,因此也可以把dropout看作是对输出矩阵的随机置0的比率.
HEAD_SIZE = 3 # 多头注意力层的head数量
VOCAB_SIZE = 1000
MAX_LEN = 64
FF_MIDDLE_DIM = 4
N = 3
# 一、文本嵌入层:定义Embeddings类来实现文本嵌入层,这里s说明代表两个一模一样的嵌入层, 他们共享参数【该类继承nn.Module, 这样就有标准层的一些功能, 这里我们也可以理解为一种模式, 我们自己实现的所有层都会这样去写】
# 1.1 构建文本嵌入层
class MyEmbedding(nn.Module):
# 类的初始化函数, 有两个参数, 【vocab_size: 指词表的大小; embedding_dim: 指转换后的词嵌入的维度】
def __init__(self, vocab_size, embedding_dim):
super(MyEmbedding, self).__init__() # 使用super的方式指明继承nn.Module的初始化函数, 我们自己实现的所有层都会这样去写.
self.vocab_size = vocab_size
self.embedding_dim = embedding_dim
self.embedding = nn.Embedding(num_embeddings=vocab_size, embedding_dim=embedding_dim) # 调用nn中的预定义层Embedding, 获得一个词嵌入对象self.embedding【vocab_size表示词汇表所有单词数量】
# 前向传播逻辑,所有层中都会有此函数,当传给该类的实例化对象参数时, 自动调用该类函数【参数word_tensor_input: 代表单词文本通过词汇映射(word2index)后的数值型张量,word_tensor_input里的每一个数字必须为0~vocab_size间的数来代表词汇表里的一个特定单词】
def forward(self, word_tensor_input):
# 将张量word_tensor_input传给self.embedding 返回词向量【math.sqrt(self.embedding_dim)具有缩放的作用,控制转换后每一个元素的数值大小尽可能离散】
word_embedded = self.embedding(word_tensor_input) * math.sqrt(self.embedding_dim)
return word_embedded
# 1.2 测试文本嵌入层
print("=" * 50, "MyEmbedding文本嵌入层测试", "=" * 50)
embedding01 = MyEmbedding(vocab_size=VOCAB_SIZE, embedding_dim=EMBEDDING_DIM)
# 输入 word_tensor_input01 形状是 torch.Size([2, 4]),word_tensor_input01 中的每一个数字代表一个单词,该数字必须处于0~10, 通过embedding将每一个数字从一维转为三维
word_tensor_input01 = Variable(torch.LongTensor([[1, 2, 4, 5], [4, 3, 2, 9]])) # 其中所有元素的数值必须在0~10之间,1、2、4、5、4、3、2、9 代表在词汇表(该词汇表中的单词总数为10)中的序号分别为1、2、4、5、4、3、2、9的单词
word_embedded01 = embedding01(word_tensor_input01)
print("=" * 200)
# 二、位置编码器:我们同样把它看做一个层, 因此会继承nn.Module
# 2.1 构建位置编码器
class PositionalEncoding(nn.Module):
def __init__(self, embedding_dim, max_len=5000, dropout=0.1): # 位置编码器类的初始化函数【共有三个参数, embedding_dim: 词嵌入维度; dropout: 置0比率; max_len: 每个句子的最大长度】
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout) # 实例化nn中预定义的Dropout层, 并将dropout传入其中, 获得对象self.dropout
pe = torch.zeros(max_len, embedding_dim) # 初始化一个形状为(max_len * embedding_dim)的位置编码矩阵【行大小max_len代表句子长度,每一行代表一个单词;列大小embedding_dim代表词向量维度】
position = torch.arange(0, max_len).unsqueeze(1) # 初始化一个形状为(max_len*1)绝对位置矩阵
div_term = torch.exp(torch.arange(0, embedding_dim, 2) * -(math.log(10000.0) / embedding_dim)) # 定义(1*embedding_dim/2)形状的变换矩阵div_term【跳跃式初始化】
pe[:, 0::2] = torch.sin(position * div_term) # 把绝对位置矩阵position经过变换矩阵div_term转换后的矩阵,再经sin()函数处理,填充在位置编码矩阵pe的偶数列
pe[:, 1::2] = torch.cos(position * div_term) # 把绝对位置矩阵position经过变换矩阵div_term转换后的矩阵,再经cos()函数处理,填充在位置编码矩阵pe的奇数列
pe = pe.unsqueeze(0) # 将二维矩阵pe拓展为三维,用于和embedding层的输出(一个三维张量)相加,
self.register_buffer('pe', pe) # 把pe位置编码矩阵注册成模型的buffer【buffer是对模型效果有帮助的,但是却不是模型结构中超参数或者参数,不需要随着优化步骤进行更新的增益对象。注册之后我们就可以在模型保存后重加载时和模型结构与参数一同被加载】
def forward(self, word_embedded): # 参数word_embedded: 表示文本序列的词嵌入表示
pe = self.pe[:, :word_embedded.size(1)] # 对pe做一些适配工作, 将这个三维张量的第二维也就是句子最大长度的那一维将切片到与输入的word_embedded的第二维相同即word_embedded.size(1),使pe与word_embedded的样式相同【因为我们默认max_len为5000一般来讲实在太大了,很难有一条句子包含5000个词汇,所以要进行与输入张量的适配】
# print("word_embedded.shape = {0}".format(word_embedded.shape))
# print("pe.shape = {0}".format(pe.shape))
word_embedded_plus_pe = word_embedded + Variable(pe, requires_grad=False) # 将pe使用Variable进行封装,但是它是不需要进行梯度求解的,因此把requires_grad设置成false.
# print("word_embedded_plus_pe.shape = {0}".format(word_embedded_plus_pe.shape))
return self.dropout(word_embedded_plus_pe) # 最后使用self.dropout对象进行'丢弃'操作, 并返回结果.
# 2.2 测试位置编码器
print("=" * 50, "PositionalEncoding位置编码器测试", "=" * 50)
dropout = DROPOUT # 置0比率为0.1
max_len = 60 # 句子最大长度
word_embedded = word_embedded01 # 文本嵌入层的输出
# 实例化PositionalEncoding层
pe = PositionalEncoding(embedding_dim=word_embedded.size(2), max_len=max_len, dropout=dropout)
pe_result = pe(word_embedded)
print("PositionalEncoding---->pe_result.shape = {0}".format(pe_result.shape))
print("=" * 200)
# 三、注意力机制的实现【输入分别是query, key, value, mask(掩码张量), dropout是nn.Dropout层的实例化对象, 默认为None】
# 1 构建注意力机制
def attention(query, key, value, mask=None, dropout=None):
d_k = query.size(-1) # 在函数中, 首先取query的最后一维的大小, 一般情况下就等同于词嵌入维度, 命名为d_k
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k) # torch.matmul()函数只对2个矩阵的最后两维度的数据进行操作。按照注意力公式, 将query【torch.Size([2, 4, 6])】与”key的转置“【torch.Size([2, 6, 4])】相乘【query、key最后一维一般都是词向量维度】, 这里面key是将最后两个维度进行转置, 再除以缩放系数根号下d_k, 得到注意力得分张量scores【这种计算方法也称为缩放点积注意力计算】
print("attention---->计算没有mask的原始scores:scores.shape = {0}----scores = \n{1}".format(scores.shape, scores)) # torch.Size([2, 4, 4])
# 接着判断是否使用掩码张量
if mask is not None:
print("attention---->mask.shape = {0}----mask = \n{1}".format(mask.shape, mask)) # torch.Size([4, 4])
scores = scores.masked_fill(mask == 0, -1e9) # 使用tensor的masked_fill方法, 将掩码张量和scores张量每个位置一一比较, 如果掩码张量处为0, 则对应的scores张量用一个非常小的数值(比如:-1e9)替换,表示此处被选中的几率几乎为0【mask的shape必须与scores的shape相同或可传播/broadcasting-semantics】
print("attention---->进行掩码之后的scores:scores.shape = {0}----scores = \n{1}".format(scores.shape, scores)) # torch.Size([2, 4, 4])
attention_weight = F.softmax(scores, dim=-1) # 对scores的最后一维进行softmax操作, 使用F.softmax方法, 第一个参数是softmax对象, 第二个是目标维度. 这样获得最终的注意力张量
if dropout is not None: # 之后判断是否使用dropout进行随机置0
attention_weight = dropout(attention_weight) # 将p_attn传入dropout对象中进行'丢弃'处理
# print("attention---->attention_weight.shape = {0}".format(attention_weight.shape)) # torch.Size([2, 3, 4, 4])
attention_result = torch.matmul(attention_weight, value) # 根据公式将attention_weight(2*3*4*4)与value(2*3*4*2)张量相乘获得最终的query注意力表示
# print("attention---->attention_result.shape = {0}".format(attention_result.shape)) # torch.Size([2, 3, 4, 2])
return attention_weight, attention_result # 返回注意力权重、最终的query注意力表示
# 2 测试注意力机制
query = key = value = pe_result # 我们令输入的query, key, value都相同【自注意机制】, 都等于位置编码的输出
print("-" * 30, "不使用mask", "-" * 30)
attention_weight01, attention_result01 = attention(query=query, key=key, value=value)
print("query.shape = key.shape = value.shape = {0}".format(query.shape))
print("attention_weight01.shape = {0}----attention_weight01 = \n{1}".format(attention_weight01.shape, attention_weight01))
print("attention_result01.shape = {0}----attention_result01 = \n{1}".format(attention_result01.shape, attention_result01))
print("-" * 200)
# 令mask为一个4x4的零张量
print("-" * 30, "使用全0的mask", "-" * 30)
zeros_matrix = Variable(torch.zeros(4, 4))
attention_weight02, attention_result02 = attention(query=query, key=key, value=value, mask=zeros_matrix)
print("attention_weight02.shape = {0}----attention_weight02 = \n{1}".format(attention_weight02.shape, attention_weight02))
print("attention_result02.shape = {0}----attention_result02 = \n{1}".format(attention_result02.shape, attention_result02))
print("-" * 200)
# 生成mask为一个4x4的下三角矩阵
print("-" * 30, "使用下三角为1的mask", "-" * 30)
ones_matrix = Variable(torch.ones(4, 4))
print("ones_matrix = \n{0}".format(ones_matrix)) # 构建一个全1的张量
subsequent_mask = Variable(torch.tril(ones_matrix)) # 使用np.triu形成上三角阵, 最后为了节约空间,再使其中的数据类型变为无符号8位整形unit8
print("subsequent_mask = \n{0}".format(subsequent_mask))
attention_weight03, attention_result03 = attention(query=query, key=key, value=value, mask=subsequent_mask)
print("attention_weight03.shape = {0}----attention_weight03 = \n{1}".format(attention_weight03.shape, attention_weight03))
print("attention_result03.shape = {0}----attention_result03 = \n{1}".format(attention_result03.shape, attention_result03))
print("-" * 200)
打印结果:
================================================== MyEmbedding文本嵌入层测试 ==================================================
========================================================================================================================================================================================================
================================================== PositionalEncoding位置编码器测试 ==================================================
PositionalEncoding---->pe_result.shape = torch.Size([2, 4, 6])
========================================================================================================================================================================================================
------------------------------ 不使用mask ------------------------------
attention---->计算没有mask的原始scores:scores.shape = torch.Size([2, 4, 4])----scores =
tensor([[[ 6.3901e+00, -4.9271e-01, -9.5974e+00, 5.7959e-01],
[-4.9271e-01, 2.7911e+00, 1.9530e+00, 9.5945e-03],
[-9.5974e+00, 1.9530e+00, 1.9369e+01, -7.3070e-01],
[ 5.7959e-01, 9.5945e-03, -7.3070e-01, 5.4320e-01]],
[[ 2.7861e+01, 7.2147e+00, 2.1429e+00, 1.2345e+01],
[ 7.2147e+00, 2.7593e+01, -6.4189e-02, -9.8363e+00],
[ 2.1429e+00, -6.4189e-02, 2.0320e+00, 3.6492e+00],
[ 1.2345e+01, -9.8363e+00, 3.6492e+00, 2.0345e+01]]],
grad_fn=<DivBackward0>)
query.shape = key.shape = value.shape = torch.Size([2, 4, 6])
attention_weight01.shape = torch.Size([2, 4, 4])----attention_weight01 =
tensor([[[9.9599e-01, 1.0211e-03, 1.1349e-07, 2.9838e-03],
[2.4468e-02, 6.5277e-01, 2.8232e-01, 4.0435e-02],
[2.6299e-13, 2.7303e-08, 1.0000e+00, 1.8651e-09],
[3.5720e-01, 2.0201e-01, 9.6352e-02, 3.4444e-01]],
[[1.0000e+00, 1.0796e-09, 6.7703e-12, 1.8260e-07],
[1.4121e-09, 1.0000e+00, 9.7423e-13, 5.5548e-17],
[1.5349e-01, 1.6887e-02, 1.3738e-01, 6.9224e-01],
[3.3559e-04, 7.8056e-14, 5.6118e-08, 9.9966e-01]]],
grad_fn=<SoftmaxBackward>)
attention_result01.shape = torch.Size([2, 4, 6])----attention_result01 =
tensor([[[-1.9156e-04, 3.3239e-01, -7.9759e-01, -7.0190e-01, 2.1240e-03,
-3.7808e+00],
[ 3.2031e-01, 1.4434e+00, 8.3568e-01, -1.0382e+00, -4.2362e-01,
1.9818e+00],
[ 2.1209e+00, 1.7579e+00, 1.7494e-01, -4.2805e-08, -1.7552e-08,
6.3107e+00],
[ 1.4589e-01, 5.5683e-01, 1.0150e-02, -7.5222e-01, 1.8561e-01,
-7.5525e-01]],
[[ 1.1106e+00, 3.3314e+00, 7.1943e-02, -2.3642e+00, 3.2394e+00,
6.3108e+00],
[-4.5048e-01, 5.0282e+00, 3.9004e+00, 4.8684e+00, 7.3417e-01,
1.6278e+00],
[-1.4924e+00, 4.8906e-01, 2.5281e-01, -4.5849e+00, 2.1102e+00,
2.3392e+00],
[-2.3192e+00, -2.2904e-01, 2.4216e-05, -5.9123e+00, 2.4525e+00,
1.8490e+00]]], grad_fn=<UnsafeViewBackward>)
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------ 使用全0的mask ------------------------------
attention---->计算没有mask的原始scores:scores.shape = torch.Size([2, 4, 4])----scores =
tensor([[[ 6.3901e+00, -4.9271e-01, -9.5974e+00, 5.7959e-01],
[-4.9271e-01, 2.7911e+00, 1.9530e+00, 9.5945e-03],
[-9.5974e+00, 1.9530e+00, 1.9369e+01, -7.3070e-01],
[ 5.7959e-01, 9.5945e-03, -7.3070e-01, 5.4320e-01]],
[[ 2.7861e+01, 7.2147e+00, 2.1429e+00, 1.2345e+01],
[ 7.2147e+00, 2.7593e+01, -6.4189e-02, -9.8363e+00],
[ 2.1429e+00, -6.4189e-02, 2.0320e+00, 3.6492e+00],
[ 1.2345e+01, -9.8363e+00, 3.6492e+00, 2.0345e+01]]],
grad_fn=<DivBackward0>)
attention---->mask.shape = torch.Size([4, 4])----mask =
tensor([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
attention---->进行掩码之后的scores:scores.shape = torch.Size([2, 4, 4])----scores =
tensor([[[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09]],
[[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09]]],
grad_fn=<MaskedFillBackward0>)
attention_weight02.shape = torch.Size([2, 4, 4])----attention_weight02 =
tensor([[[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500]],
[[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500]]], grad_fn=<SoftmaxBackward>)
attention_result02.shape = torch.Size([2, 4, 6])----attention_result02 =
tensor([[[ 0.4432, 0.8668, 0.1733, -0.6976, 0.0615, 0.6716],
[ 0.4432, 0.8668, 0.1733, -0.6976, 0.0615, 0.6716],
[ 0.4432, 0.8668, 0.1733, -0.6976, 0.0615, 0.6716],
[ 0.4432, 0.8668, 0.1733, -0.6976, 0.0615, 0.6716]],
[[-0.5042, 2.1273, 1.3132, -1.2356, 1.4300, 2.5633],
[-0.5042, 2.1273, 1.3132, -1.2356, 1.4300, 2.5633],
[-0.5042, 2.1273, 1.3132, -1.2356, 1.4300, 2.5633],
[-0.5042, 2.1273, 1.3132, -1.2356, 1.4300, 2.5633]]],
grad_fn=<UnsafeViewBackward>)
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------ 使用下三角为1的mask ------------------------------
ones_matrix =
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
subsequent_mask =
tensor([[1., 0., 0., 0.],
[1., 1., 0., 0.],
[1., 1., 1., 0.],
[1., 1., 1., 1.]])
attention---->计算没有mask的原始scores:scores.shape = torch.Size([2, 4, 4])----scores =
tensor([[[ 6.3901e+00, -4.9271e-01, -9.5974e+00, 5.7959e-01],
[-4.9271e-01, 2.7911e+00, 1.9530e+00, 9.5945e-03],
[-9.5974e+00, 1.9530e+00, 1.9369e+01, -7.3070e-01],
[ 5.7959e-01, 9.5945e-03, -7.3070e-01, 5.4320e-01]],
[[ 2.7861e+01, 7.2147e+00, 2.1429e+00, 1.2345e+01],
[ 7.2147e+00, 2.7593e+01, -6.4189e-02, -9.8363e+00],
[ 2.1429e+00, -6.4189e-02, 2.0320e+00, 3.6492e+00],
[ 1.2345e+01, -9.8363e+00, 3.6492e+00, 2.0345e+01]]],
grad_fn=<DivBackward0>)
attention---->mask.shape = torch.Size([4, 4])----mask =
tensor([[1., 0., 0., 0.],
[1., 1., 0., 0.],
[1., 1., 1., 0.],
[1., 1., 1., 1.]])
attention---->进行掩码之后的scores:scores.shape = torch.Size([2, 4, 4])----scores =
tensor([[[ 6.3901e+00, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-4.9271e-01, 2.7911e+00, -1.0000e+09, -1.0000e+09],
[-9.5974e+00, 1.9530e+00, 1.9369e+01, -1.0000e+09],
[ 5.7959e-01, 9.5945e-03, -7.3070e-01, 5.4320e-01]],
[[ 2.7861e+01, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[ 7.2147e+00, 2.7593e+01, -1.0000e+09, -1.0000e+09],
[ 2.1429e+00, -6.4189e-02, 2.0320e+00, -1.0000e+09],
[ 1.2345e+01, -9.8363e+00, 3.6492e+00, 2.0345e+01]]],
grad_fn=<MaskedFillBackward0>)
attention_weight03.shape = torch.Size([2, 4, 4])----attention_weight03 =
tensor([[[1.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00],
[3.6130e-02, 9.6387e-01, 0.0000e+00, 0.0000e+00],
[2.6299e-13, 2.7303e-08, 1.0000e+00, 0.0000e+00],
[3.5720e-01, 2.0201e-01, 9.6352e-02, 3.4444e-01]],
[[1.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00],
[1.4121e-09, 1.0000e+00, 0.0000e+00, 0.0000e+00],
[4.9873e-01, 5.4871e-02, 4.4640e-01, 0.0000e+00],
[3.3559e-04, 7.8056e-14, 5.6118e-08, 9.9966e-01]]],
grad_fn=<SoftmaxBackward>)
attention_result03.shape = torch.Size([2, 4, 6])----attention_result03 =
tensor([[[ 0.0000e+00, 3.3245e-01, -8.0233e-01, -7.0148e-01, 0.0000e+00,
-3.7956e+00],
[-4.1617e-01, 1.4024e+00, 1.1555e+00, -1.4997e+00, -6.8248e-01,
3.1322e-01],
[ 2.1209e+00, 1.7579e+00, 1.7494e-01, -4.1762e-08, -1.9332e-08,
6.3107e+00],
[ 1.4589e-01, 5.5683e-01, 1.0150e-02, -7.5222e-01, 1.8561e-01,
-7.5525e-01]],
[[ 1.1106e+00, 3.3314e+00, 7.1943e-02, -2.3642e+00, 3.2394e+00,
6.3108e+00],
[-4.5048e-01, 5.0282e+00, 3.9004e+00, 4.8684e+00, 7.3417e-01,
1.6278e+00],
[ 3.7006e-01, 2.1069e+00, 8.2145e-01, -1.5964e+00, 1.3409e+00,
3.4453e+00],
[-2.3192e+00, -2.2904e-01, 2.4216e-05, -5.9123e+00, 2.4525e+00,
1.8490e+00]]], grad_fn=<UnsafeViewBackward>)
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
四、多头自注意力类
class MultiHeadedAttention(nn.Module):
# 在类的初始化时, 会传入三个参数,head_size代表头数,embedding_dim代表词嵌入的维度, dropout代表进行dropout操作时置0比率,默认是0.1
def __init__(self, head_size, embedding_dim, dropout=0.1):
super(MultiHeadedAttention, self).__init__()
self.head_size = head_size
# print("embedding_dim = {0}----head_size = {1}".format(embedding_dim, head_size))
assert embedding_dim % head_size == 0 # 在函数中,首先使用了一个测试中常用的assert语句,判断head_size是否能被embedding_dim整除【这是因为我们之后要给每个头分配等量的词特征.也就是embedding_dim/head_size个.】
self.d_k = embedding_dim // head_size # 整除得到每个头获得的分割词向量维度d_k【比如:词向量总维度为6,被3个head平分,每个head获得词向量中2个维度的数据】
self.my_linears = clones(nn.Linear(embedding_dim, embedding_dim), 4) # 然后获得线性层对象,通过nn的Linear实例化,它的内部变换矩阵是embedding_dim x embedding_dim【一定是一个方阵】,然后使用clones函数克隆四个【Q,K,V各需要一个,最后拼接的矩阵还需要一个,因此一共是四个】
self.attention_result = None # 初始化最后得到的注意力张量attention_result,现在还没有结果所以为None.
self.dropout = nn.Dropout(p=dropout) # 最后就是一个self.dropout对象,它通过nn中的Dropout实例化而来,置0比率为传进来的参数dropout.
# 前向逻辑函数, 它的输入参数有四个,前三个就是注意力机制需要的Q, K, V,最后一个是注意力机制中可能需要的mask掩码张量,默认是None.
def forward(self, query, key, value, mask=None):
if mask is not None: # 如果存在掩码张量mask
mask = mask.unsqueeze(0) # 使用unsqueeze拓展维度,代表多头中的各个头
batch_size = query.size(0) # 接着,我们获得一个batch_size的变量,他是query尺寸的第1个数字,代表有多少条样本.
# print("MultiHeadedAttention---->query----传入的query.shape = {0}----第一维度表示句子数量,第二维度表示句子长度,第三维度表示每个单词的词向量维度".format(query.shape)) # torch.Size([2, 4, 6])
# print("MultiHeadedAttention---->key----传入的key.shape = {0}----第一维度表示句子数量,第二维度表示句子长度,第三维度表示每个单词的词向量维度".format(key.shape)) # torch.Size([2, 4, 6])
# print("MultiHeadedAttention---->value----传入的value.shape = {0}----第一维度表示句子数量,第二维度表示句子长度,第三维度表示每个单词的词向量维度".format(value.shape)) # torch.Size([2, 4, 6])
# 进入多头处理环节
# 做完线性变换后,开始为每个头分割输入,这里使用view方法对线性变换的结果进行维度重塑,多加了一个维度h,代表头数。这样就意味着每个头可以获得一部分词特征组成的句子。
# 然后对第二维和第三维进行转置操作,为了让代表句子长度维度和词向量维度能够相邻,这样注意力机制才能找到词义与句子位置的关系,
# attention函数利用的是原始输入的倒数第一和第二维.这样我们就得到了每个头的输入.
# query, key, value = [my_linear(x).view(batch_size, -1, self.head, self.d_k).transpose(1, 2) for my_linear, x in zip(self.linears, (query, key, value))] # zip()函数返回一个元祖列表
query = self.my_linears[0](query).view(batch_size, -1, self.head_size, self.d_k)
# print("MultiHeadedAttention---->query----通过view变换形状:query.shape = {0}----第一维度表示句子数量,第二维度表示句子长度,第三维度表示head_size,第四维度表示每个head从单词的词向量总维度中分到的维度数量".format(query.shape)) # torch.Size([2, 4, 3, 2])
query = query.transpose(1, 2)
# print("MultiHeadedAttention---->query----通过transpose变换形状:query.shape = {0}".format(query.shape)) # torch.Size([2, 3, 4, 2]),其中3为head_size的数量
key = self.my_linears[0](key).view(batch_size, -1, self.head_size, self.d_k)
# print("MultiHeadedAttention---->key----通过view变换形状:key.shape = {0}----第一维度表示句子数量,第二维度表示句子长度,第三维度表示head_size,第四维度表示每个head从单词的词向量总维度中分到的维度数量".format(key.shape)) # torch.Size([2, 4, 3, 2])
key = key.transpose(1, 2)
# print("MultiHeadedAttention---->key----通过transpose变换形状:key.shape = {0}".format(key.shape)) # torch.Size([2, 3, 4, 2])
value = self.my_linears[0](value).view(batch_size, -1, self.head_size, self.d_k)
# print("MultiHeadedAttention---->value----通过view变换形状:value.shape = {0}----第一维度表示句子数量,第二维度表示句子长度,第三维度表示head_size,第四维度表示每个head从单词的词向量总维度中分到的维度数量".format(value.shape)) # torch.Size([2, 4, 3, 2])
value = value.transpose(1, 2)
# print("MultiHeadedAttention---->value----通过transpose变换形状:value.shape = {0}".format(value.shape)) # torch.Size([2, 3, 4, 2])
# 注意力计算
self.attention_weight, self.attention_result = attention(query, key, value, mask=mask, dropout=self.dropout) # 得到每个头的输入后,接下来就是将他们传入到attention中【这里直接调用我们之前实现的attention函数.同时也将mask和dropout传入其中】
# print("MultiHeadedAttention---->self.attention_weight.shape = {0}".format(self.attention_weight.shape)) # torch.Size([2, 3, 4, 4])
# print("MultiHeadedAttention----> self.attention_result.shape = {0}".format(self.attention_result.shape)) # torch.Size([2, 3, 4, 2])
# 合并多头分别计算attention的结果
self.attention_result = self.attention_result.transpose(1, 2) # 通过多头注意力计算后,得到每个头计算结果组成的(4*2)维张量,我们需要将其转换为输入的形状以方便后续的计算【进行第一步处理环节的逆操作,对第二和第三维进行转置】
# print("MultiHeadedAttention----> 通过transpose变换形状:self.attention_result.shape = {0}".format(self.attention_result.shape)) # torch.Size([2, 4, 3, 2])
self.multi_headed_attention_result = self.attention_result.contiguous().view(batch_size, -1, self.head_size * self.d_k) # 使用view重塑形状,变成和输入形状相同,将最后一维大小恢复为embedding_dim【contiguous方法的作用就是能够让转置后的张量应用view方法,否则将无法直接使用】
# print("MultiHeadedAttention---->最终形状:self.multi_headed_attention_result.shape = {0}".format(self.multi_headed_attention_result.shape)) # torch.Size([2, 4, 3, 2])
# 经过最后一层线性变换
multi_headed_attention_result = self.my_linears[-1](self.multi_headed_attention_result) # 最后使用线性层列表中的最后一个线性层对attention_result进行线性变换得到最终的多头注意力结构的输出.
return multi_headed_attention_result
五、前馈全连接层类
# 前馈全连接层
class FeedForward(nn.Module):
def __init__(self, embedding_dim, ff_middle_dim, dropout=0.1): # embedding_dim是线性层的输入维度也是第二个线性层的输出维度,因为我们希望输入通过前馈全连接层后输入和输出的维度不变.ff_middle_dim就是第二个线性层的输入维度和第一个线性层的输出维度.
super(FeedForward, self).__init__()
self.linear01 = nn.Linear(embedding_dim, ff_middle_dim) # 使用nn实例化线性层对象self.linear01
self.linear02 = nn.Linear(ff_middle_dim, embedding_dim) # 使用nn实例化线性层对象self.linear02
self.dropout = nn.Dropout(dropout) # 使用nn默认的Dropout实例化对象self.dropout
def forward(self, x): # 输入参数为x,代表来自上一层(多头注意力层)的输出
# 首先经过第一个线性层,然后使用Funtional中relu函数进行激活,
# 之后再使用dropout进行随机置0,最后通过第二个线性层linear02,返回最终结果.
return self.linear02(self.dropout(F.relu(self.linear01(x))))
六、规范化层
# 规范化层类【元素的规范化值=(元素的原始值-元素所在维度均值)/元素所在维度方差】
class MyLayerNorm(nn.Module):
def __init__(self, embedding_dim, eps=1e-6): # embedding_dim, 表示词嵌入的维度;eps它是一个足够小的数, 在规范化公式的分母中出现,防止分母为0.默认是1e-6.
super(MyLayerNorm, self).__init__()
self.eps = eps
# 参数a、b的作用:如果直接对上一层得到的结果做规范化公式计算,将会改变结果的正常表征。所以需要使用辅助参数作为调节因子,使规范化后的数据即能满足规范化要求,又能不改变针对目标的表征.
self.a = nn.Parameter(torch.ones(embedding_dim)) # 根据embedding_dim的形状初始化规范化层的参数a(全1张量)【使用nn.parameter封装,代表a是模型的参数,a会跟随着模型一起被训练更新】
self.b = nn.Parameter(torch.zeros(embedding_dim)) # 根据embedding_dim的形状初始化规范化层的参数b(全0张量)【使用nn.parameter封装,代表b是模型的参数,b会跟随着模型一起被训练更新】
def forward(self, x): # 输入参数x代表来自上一层(前馈全连接层)的输出
# print("-" * 50, "MyLayerNorm:开始", "-" * 50)
# print("MyLayerNorm---->x.shape = {0}".format(x.shape)) # torch.Size([2, 4, 6])
# μ0 = x.mean(-1, keepdim=False) # 用于对比【-1表示对最后一个维度的数据求均值】
# print("MyLayerNorm---->keepdim=False----μ0.shape = {0}".format(μ0.shape)) # torch.Size([2, 4])
# print("MyLayerNorm---->keepdim=False----μ0 = {0}".format(μ0))
μ = x.mean(-1, keepdim=True) # 【-1表示对x的最后一个维度的所有数据求均值】,【keepdim=True表示保持输出维度与输入维度一致,以便后续计算】【如果keepdim=True,则输出shape为torch.Size([2, 4, 1]),否则为torch.Size([2, 4])】
# print("MyLayerNorm---->keepdim=True----μ.shape = {0}".format(μ.shape)) # torch.Size([2, 4, 1])
# print("MyLayerNorm---->keepdim=True----μ = {0}".format(μ))
σ = x.std(-1, keepdim=True) # 【-1表示对x的最后一个维度的所有数据求标准差】,【keepdim=True表示保持输出维度与输入维度一致,以便后续计算】,【如果keepdim=True,则输出shape为torch.Size([2, 4, 1]),否则为torch.Size([2, 4])】
# print("MyLayerNorm---->keepdim=True----σ.shape = {0}".format(σ.shape)) # torch.Size([2, 4, 1])
# print("MyLayerNorm---->keepdim=True----σ = {0}".format(σ))
norm_result = (x - μ) / (σ + self.eps) # 根据规范化公式,用x减去均值除以标准差获得规范化的结果,【eps它是一个足够小的数, 在分母中出现,防止分母为0】
# print("MyLayerNorm---->norm_result.shape = {0}".format(norm_result.shape))
# print("MyLayerNorm---->self.a.shape = {0}".format(self.a.shape))
# print("MyLayerNorm---->self.b.shape = {0}".format(self.b.shape))
norm_result = self.a * norm_result + self.b # 最后对结果乘以我们的缩放参数,即a,*号代表同型点乘,即对应位置进行乘法操作,加上位移参数b.返回即可.
# print("-" * 50, "MyLayerNorm:结束", "-" * 50)
return norm_result
七、子层连接结构
# 子层连接结构【使用SublayerConnection来实现子层连接结构的类】
class SublayerConnection(nn.Module):
def __init__(self, embedding_dim, dropout=0.1): # embedding_dim:一般是都是词嵌入维度的大小,dropout本身是对模型结构中的节点数进行随机抑制的比率,又因为节点被抑制等效就是该节点的输出都是0,因此也可以把dropout看作是对输出矩阵的随机置0的比率.
super(SublayerConnection, self).__init__()
self.myLayerNorm = MyLayerNorm(embedding_dim) # 实例化了规范化对象self.norm
self.dropout = nn.Dropout(p=dropout) # 使用nn中预定义的droupout实例化一个self.dropout对象.
def forward(self, x, sublayer_fn): # 前向逻辑函数【x:代表上一个层或者子层的输出作为本子层的输入,sublayer_fn:代表该子层连接中的子层函数】
sublayer_output = self.dropout(sublayer_fn(self.myLayerNorm(x))) # 首先对x进行规范化,将规范化后的结果传给子层处理,对子层进行dropout操作【dropout操作随机停止一些网络中神经元的作用,来防止过拟合. 】
# print("SublayerConnection---->x.shape = {0}----sublayer_output.shape = {1}".format(x.shape, sublayer_output.shape))
output = x + sublayer_output # 最后的add操作【因为存在跳跃连接,所以是将输入x与dropout后的sublayer子层输出结果sublayer_output相加作为最终的子层连接输出.】
return output
5、6、7步骤可通过类PositionwiseFeedForward(包括:前馈全连接层、残差连接、规范化层)来统一实现
class PoswiseFeedForwardNet(nn.Module):
'''
残差链接 & 规范化层 & 前馈层
'''
def __init__(self, hidden_size, d_ff, dropout=0.1):
super(PoswiseFeedForwardNet, self).__init__()
self.relu = nn.ReLU()
self.w1 = nn.Linear(in_channels=hidden_size, out_channels=d_ff, kernel_size=1)
self.w2 = nn.Linear(in_channels=d_ff, out_channels=hidden_size, kernel_size=1)
self.dropout = nn.Dropout(dropout)
self.layer_norm = LayerNormalization(hidden_size)
def forward(self, inputs):
# inputs: [b_size x len_q x hidden_size]
residual = inputs
output = self.relu(self.w1(inputs.transpose(1, 2)))
# outputs: [b_size x len_q x hidden_size]
output = self.w2(output).transpose(1, 2)
output = self.dropout(output)
return self.layer_norm(residual + output)
论文中提到,这个公式还可以用两个核大小为1的一维卷积来解释,卷积的输入输出都是 d m o d e l = 512 d_{model}=512 dmodel=512,中间层的维度是 d f f = 2048 d_{ff}=2048 dff=2048。最后经过残差连接和 Layer normalization
class PoswiseFeedForwardNet(nn.Module):
'''
残差链接 & 规范化层 & 前馈层
'''
def __init__(self, hidden_size, d_ff, dropout=0.1):
super(PoswiseFeedForwardNet, self).__init__()
self.relu = nn.ReLU()
self.conv1 = nn.Conv1d(in_channels=hidden_size, out_channels=d_ff, kernel_size=1)
self.conv2 = nn.Conv1d(in_channels=d_ff, out_channels=hidden_size, kernel_size=1)
self.dropout = nn.Dropout(dropout)
self.layer_norm = LayerNormalization(hidden_size)
def forward(self, inputs):
# inputs: [b_size x len_q x hidden_size]
residual = inputs
output = self.relu(self.conv1(inputs.transpose(1, 2)))
# outputs: [b_size x len_q x hidden_size]
output = self.conv2(output).transpose(1, 2)
output = self.dropout(output)
return self.layer_norm(residual + output)
八、编码器层
# 编码器层【使用EncoderLayer类实现编码器层】
class EncoderLayer(nn.Module):
# embedding_dim:词嵌入维度的大小,它也将作为我们编码器层的大小,self_attention_layer:多头自注意力子层实例化对象, 并且是自注意力机制;feed_forward_layer:前馈全连接层实例化对象
def __init__(self, embedding_dim, self_attention_layer, feed_forward_layer, dropout):
super(EncoderLayer, self).__init__()
self.self_attention_layer = self_attention_layer
self.feed_forward_layer = feed_forward_layer
self.embedding_dim = embedding_dim
self.sublayer_connection = clones(SublayerConnection(embedding_dim, dropout), 2) # 编码器层中有两个子层连接结构, 所以使用clones函数进行克隆【此时子层连接结构里的sublayer_fn上没有被定义传入】
def forward(self, x, mask): # x:上一层的输出;mask:掩码张量.
sublayer_fn01 = lambda x: self.self_attention_layer(query=x, key=x, value=x, mask=mask)
sublayer_fn02 = lambda x: self.feed_forward_layer(x)
x = self.sublayer_connection[0](x, sublayer_fn01) # 第一个子层连接结构,包含多头自注意力子层
x = self.sublayer_connection[1](x, sublayer_fn02) # 第二个子层连接结构,包含前馈全连接子层
return x
九、编码器
# 编码器【使用Encoder类来实现编码器】
class Encoder(nn.Module):
def __init__(self, encoderLayer, N): # encoderLayer: 代表编码器层; N: 编码器层的个数
super(Encoder, self).__init__()
self.encoderLayers = clones(encoderLayer, N) # 首先使用clones函数克隆N个编码器层放在self.encoderLayers中
self.myLayerNorm = MyLayerNorm(encoderLayer.embedding_dim) # 实例化一个规范化层, 它将用在编码器的最后面.
def forward(self, source_embedded_x, mask): # source_embedded_x:来自上一层的输入(源语言数据的词嵌入表示); mask: 掩码张量
for encoderLayer in self.encoderLayers: # 将输入source_embedded_x分别通过所有克隆的编码器层,每经过一个编码器层都会得到一个新的source_embedded_x
source_embedded_x = encoderLayer(source_embedded_x, mask)
encoder_result = self.myLayerNorm(source_embedded_x) # 最后将x通过规范化层的对象self.myLayerNorm进行处理
return encoder_result
十、解码器层
# 解码器层【使用DecoderLayer的类实现解码器层:作为解码器的组成单元, 每个解码器层根据给定的输入向目标方向进行特征提取操作,即解码过程.】
# 构建解码器层【最终输出由”编码器层的最终输出“、”目标语言数据张量“一同作为解码器层的输入的特征提取结果】
class DecoderLayer(nn.Module):
# 初始化函数的参数有5个【embedding_dim: 词嵌入的维度大小(同时也代表解码器层的尺寸); self_attention_layer: 多头自注意力对象(Q=K=V); src_attention_layer: 多头常规注意力对象(Q!=K=V); feed_forward_layer: 前馈全连接层对象
def __init__(self, embedding_dim, self_attention_layer, src_attention_layer, feed_forward_layer, dropout=0.1):
super(DecoderLayer, self).__init__()
self.embedding_dim = embedding_dim
self.self_attention_layer = self_attention_layer
self.src_attention_layer = src_attention_layer
self.feed_forward_layer = feed_forward_layer
self.sublayer_connection = clones(SublayerConnection(embedding_dim, dropout), 3) # 使用clones函数克隆三个子层连接对象【解码器层包含3个子层连接结构】
def forward(self, x, memory, source_mask, target_mask): # forward函数中的参数有4个【x:来自上一层的输入(目标语言数据的词嵌入表示); mermory: 编码器层的最终输出(源语言数据语义存储变量), source_mask: 源语言数据的掩码张量; target_mask:目标语言数据的掩码张量】
sublayer_fn01 = lambda x: self.self_attention_layer(query=x, key=x, value=x, mask=target_mask) # sublayer使用多头自注意力层,所以Q,K,V都是x,【target_mask是目标语言数据掩码张量,这时要对目标语言数据进行遮掩,因为此时模型可能还没有生成任何目标语言数据,比如在解码器准备生成第一个字符或词汇时,我们其实已经传入了第一个字符以便计算损失,但是我们不希望在生成第一个字符时模型能利用第一个字符以及之后的信息,因此我们会将其遮掩,同样生成第二个字符或词汇时,模型只能使用第一个字符或词汇信息,第二个字符以及之后的信息都不允许被模型使用.】
x = self.sublayer_connection[0](x, sublayer_fn01) # 第一个子层连接结构
sublayer_fn02 = lambda x: self.src_attention_layer(query=x, key=memory, value=memory, mask=source_mask) # sublayer使用多头常规注意力机制,q是输入x; k,v是编码层输出memory【source_mask是源语言数据掩码张量,进行源语言数据遮掩的原因并非是抑制信息泄漏,而是遮蔽掉对结果没有意义的字符而产生的注意力值, 以此提升模型效果和训练速度】
x = self.sublayer_connection[1](x, sublayer_fn02) # 第二个子层连接结构
sublayer_fn03 = lambda x: self.feed_forward_layer(x) # sublayer使用前馈全连接子层
x = self.sublayer_connection[2](x, sublayer_fn03) # 第三个子层连接结构
return x # 最终输出由”编码器层的最终输出“、”目标语言数据张量“一同作为解码器层的输入的特征提取结果
十一、解码器
# 解码器【根据”编码器层的最终输出“&“解码器上一次预测的结果” 对下一次可能出现的'值'进行特征表示】
class Decoder(nn.Module):
def __init__(self, decoderLayers, N): # decoderLayer: 代表解码器层; N: 解码器层的个数
super(Decoder, self).__init__()
self.decoderLayers = clones(decoderLayers, N) # 首先使用clones函数克隆N个解码器层放在self.decoderLayers数组中
self.myLayerNorm = MyLayerNorm(decoderLayers.embedding_dim) # 实例化一个规范化层, 它将用在解码器的最后面.
def forward(self, target_embedded_x, memory, source_mask, target_mask): # forward函数中的参数有4个【target_embedded_x:来自上一层的输入(目标语言数据的词嵌入表示); mermory: 编码器层的最终输出(源语言数据语义存储变量), source_mask: 源语言数据的掩码张量; target_mask:目标语言数据的掩码张量】
for decoderLayer in self.decoderLayers: # 将输入target_embedded分别通过所有克隆的编码器层,每经过一个编码器层都会得到一个新的target_embedded
target_embedded_x = decoderLayer(target_embedded_x, memory, source_mask, target_mask)
decoder_result = self.myLayerNorm(target_embedded_x) # 最后将target_embedded_x通过规范化层的对象self.myLayerNorm进行处理
return decoder_result
十二、输出部分
# 输出部分
class Generator(nn.Module):
def __init__(self, embedding_dim, target_vocab_size): # embedding_dim: 代表词嵌入维度, target_vocab_size: 代表目标词表大小
# print("Generator---->embedding_dim = {0}----target_vocab_size = {1}".format(embedding_dim, target_vocab_size))
super(Generator, self).__init__()
self.project = nn.Linear(embedding_dim, target_vocab_size) # 使用nn中的预定义线性层进行实例化
def forward(self, x): # 前向逻辑函数中输入是上一层的输出张量x
# print("Generator---->x.shape = {0}".format(x.shape))
x = self.project(x) # 使用self.project对x进行线性变化【转换维度的作用】
generator_output = F.log_softmax(x, dim=-1) # 使最后一维的向量中的数字缩放到0-1的概率值域内, 并满足他们的和为1。在这里之所以使用log_softmax是因为和我们这个pytorch版本的损失函数实现有关, 在其他版本中将修复.【log_softmax就是对softmax的结果又取了对数, 因为对数函数是单调递增函数, 因此对最终我们取最大的概率值没有影响. 最后返回结果即可】
# print("Generator---->generator_output.shape = {0}".format(generator_output.shape))
return generator_output
十三、编码器-解码器结构
# 编码器-解码器结构
class EncoderDecoder(nn.Module):
def __init__(self, encoder, decoder, source_embedding_fn, target_embedding_fn, generator): # 初始化函数中有5个参数【encoder: 编码器对象, decoder: 解码器对象, source_embedding_fn:源语言数据词嵌入函数, target_embedding_fn:目标语言数据词嵌入函数, generator:输出部分的类别生成器对象】
super(EncoderDecoder, self).__init__()
self.encoder = encoder
self.decoder = decoder
self.source_embedding_fn = source_embedding_fn
self.target_embedding_fn = target_embedding_fn
self.generator = generator
def forward(self, source_tensor, target_tensor, source_mask, target_mask): # 在forward函数中,有四个参数【source:源语言数据(数值型张量); target: 目标语言数据(数值型张量); source_mask: 源语言数据的掩码张量; target_mask:目标语言数据的掩码张量】
encoder_result = self.encode(source_tensor=source_tensor, source_mask=source_mask) # 将source, source_mask传入编码函数, 得到编码器最终输出结果
decoder_result = self.decode(target_tensor=target_tensor, memory=encoder_result, source_mask=source_mask, target_mask=target_mask)
# print("EncoderDecoder---->decoder_result.shape = {0}".format(decoder_result.shape))
return decoder_result
def encode(self, source_tensor, source_mask): # 编码函数【source_tensor: 源语言数据张量; source_mask: 源语言数据的掩码张量】
source_embedded = self.source_embedding_fn(source_tensor) # 将源语言数据张量转为词向量
encoder_result = self.encoder(source_embedded, source_mask) # 将源语言词向量经过编码器编码得到编码器最终输出
return encoder_result
# decoder的作用:基于输入的目标语言某个单词张量(target_tensor)、编码器最终输出(memory,对源语言一句待翻译文本的编码结果)预测并输出接下来的目标语言某个单词张量(decoder_output)。
def decode(self, target_tensor, memory, source_mask, target_mask): # 解码函数【target_tensor: 目标语言数据张量; memory: 编码器最终输出; source_mask: 源语言数据的掩码张量; target_mask:目标语言数据的掩码张量】
target_embedded = self.target_embedding_fn(target_tensor) # 将目标语言数据张量转为词向量
decoder_output = self.decoder(target_embedded, memory, source_mask, target_mask)
return decoder_output
十四、Transfomer模型构建函数
# Transfomer模型构建函数: 该函数用来构建模型, 有7个参数,【source_vocab_size: 源数据特征(词汇)总数; target_vocab_size: 目标数据特征(词汇)总数; N: 编码器和解码器堆叠数; embedding_dim: 词向量映射维度; ff_middle_dim: 前馈全连接层中变换矩阵的维度; head_size: 多头注意力结构中的多头数; dropout: 置零比率】
def build_model(source_vocab_size, target_vocab_size, N=2, max_len=64, embedding_dim=512, head_size=8, ff_middle_dim=2048, dropout=0.1): # 这些都是超参数,需要调试来优化模型
my_deep_copy = copy.deepcopy # 首先得到一个深度拷贝命令,接下来很多结构都需要进行深度拷贝,来保证他们彼此之间相互独立,不受干扰.
attention_layer = MultiHeadedAttention(head_size=head_size, embedding_dim=embedding_dim) # 实例化了多头注意力类
feed_forward_layer = FeedForward(embedding_dim=embedding_dim, ff_middle_dim=ff_middle_dim, dropout=dropout) # 然后实例化前馈全连接类
position_encoder = PositionalEncoding(embedding_dim=embedding_dim, max_len=max_len, dropout=dropout)
# 根据Transfomer模型结构图, 最外层是EncoderDecoder,在 EncoderDecoder中,分别是1、编码器层; 2、解码器层; 3、源数据Embedding层和位置编码组成的有序结构,4、目标数据Embedding层和位置编码组成的有序结构; 5、类别生成器层.
model = EncoderDecoder(
Encoder(EncoderLayer(embedding_dim, my_deep_copy(attention_layer), my_deep_copy(feed_forward_layer), dropout), N), # 在编码器层中有2个子层【self_attention_layer子层、前馈全连接子层】
Decoder(DecoderLayer(embedding_dim, my_deep_copy(attention_layer), my_deep_copy(attention_layer), my_deep_copy(feed_forward_layer), dropout), N), # 在解码器层中有3个子层【self_attention_layer子层、src_attention_layer子层、前馈全连接子层】
nn.Sequential(MyEmbedding(source_vocab_size, embedding_dim), my_deep_copy(position_encoder)),
nn.Sequential(MyEmbedding(target_vocab_size, embedding_dim), my_deep_copy(position_encoder)),
Generator(embedding_dim, target_vocab_size))
# 模型结构完成后,接下来就是初始化模型中的参数(比如线性层中的变换矩阵)【一但判断参数的维度大于1,则会将其初始化成一个服从均匀分布的矩阵; 如果维度为 1,直接初始化未0即可】
for p in model.parameters():
if p.dim() > 1:
nn.init.xavier_uniform(p)
return model
十五、工具函数
# 1 克隆函数, 因为在多头注意力机制的实现中, 用到多个结构相同的线性层. 我们将使用clone函数将他们一同初始化在一个网络层列表对象中. 之后的结构中也会用到该函数.
def clones(module, N): # 用于生成相同网络层的克隆函数, 它的参数module表示要克隆的目标网络层, N代表需要克隆的数量
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)]) # 在函数中, 我们通过for循环对module进行N次深度拷贝, 使其每个module成为独立的层,然后将其放在nn.ModuleList类型的列表中存放.
# 2 构建 Sequence掩码张量
def subsequent_mask(size):
attn_shape = (1, size, size) # 定义掩码张量的形状【参数size是掩码张量最后两个维度的大小, attn_shape的最后两维形成一个方阵】
ones_matrix = np.ones(attn_shape)
# print("ones_matrix = \n{0}".format(ones_matrix)) # 构建一个全1的张量
subsequent_mask = np.triu(ones_matrix, k=1).astype('uint8') # 使用np.triu形成上三角阵, 最后为了节约空间,再使其中的数据类型变为无符号8位整形unit8
subsequent_mask = torch.from_numpy(subsequent_mask) == 0 # 将numpy类型转化为torch中的tensor【与0比较后返回True、False】
# print("subsequent_mask = \n{0}".format(subsequent_mask))
return subsequent_mask
# 测试:生成20×20的掩码张量
# size = 20 # 设置生成的掩码张量的最后两维的大小
# sm = subsequent_mask(size)
# print("sm = \n{0}".format(sm))
# plt.figure(figsize=(5, 5))
# plt.imshow(sm[0])
# print("=" * 200)
# 3 Batch【Object for holding a batch of data with mask during training. 它能够对原始样本数据生成对应批次的掩码张量】
class Batch:
def __init__(self, src, trg=None, pad=0):
print("使用Batch工具类组装data_generator()函数生成的source_tensor、target_tensor:\nsrc={0}\ntrg={1}\npad={2}".format(src, trg, pad))
self.src = src
self.src_mask = (src != pad).unsqueeze(-2)
if trg is not None:
self.trg = trg[:, :-1]
self.trg_y = trg[:, 1:]
self.trg_mask = self.make_std_mask(self.trg, pad)
self.ntokens = (self.trg_y != pad).data.sum()
print("Batch---->self.trg.shape={0}".format(self.trg.shape))
print("Batch---->self.trg_y.shape={0}".format(self.trg_y.shape))
print("Batch---->self.trg_mask.shape={0}".format(self.trg_mask.shape))
print("Batch---->self.ntokens={0}".format(self.ntokens))
@staticmethod
def make_std_mask(tgt, pad): # "Create a mask to hide padding and future words.
tgt_mask = (tgt != pad).unsqueeze(-2)
tgt_mask = tgt_mask & Variable(subsequent_mask(tgt.size(-1)).type_as(tgt_mask.data))
return tgt_mask
# 4 优化器生成函数
class NoamOpt:
def __init__(self, model_size, factor, warmup, optimizer):
self.optimizer = optimizer
self._step = 0
self.warmup = warmup
self.factor = factor
self.model_size = model_size
self._rate = 0
def step(self): # Update parameters and rate
self._step += 1
rate = self.rate()
for p in self.optimizer.param_groups:
p['lr'] = rate
self._rate = rate
self.optimizer.step()
def rate(self, step=None): # Implement `lrate` above
if step is None:
step = self._step
return self.factor * (self.model_size ** (-0.5) * min(step ** (-0.5), step * self.warmup ** (-1.5)))
# 优化器工具包 get_std_optimizer, 该工具用于获得标准的针对Transformer标准化的模型优化器 【该标准优化器基于Adam优化器, 使其对序列到序列的任务更有效.】
def get_std_optimizer(model):
return NoamOpt(model_size=model.source_embedding_fn[0].embedding_dim, factor=2, warmup=4000, optimizer=torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))
# 5 标签平滑损失函数, 该工具用于标签平滑, 标签平滑的作用就是小幅度的改变原有标签值的值域【因为在理论上即使是人工的标注数据也可能并非完全正确, 会受到一些外界因素的影响而产生一些微小的偏差。因此使用标签平滑来弥补这种偏差, 减少模型对某一条规律的绝对认知, 以防止过拟合】
class CriterionWithLabelSmoothing(nn.Module):
# 第一个参数size代表目标数据的词汇总数, 也是模型最后一层得到张量的最后一维大小; 第二个参数padding_idx表示要将那些tensor中的数字替换成0, 一般padding_idx=0表示不进行替换; 第三个参数smoothing, 表示标签的平滑程度, 如原来标签的表示值为1, 则平滑后它的值域变为[1-smoothing, 1+smoothing]
def __init__(self, size, padding_idx, smoothing=0.0):
super(CriterionWithLabelSmoothing, self).__init__()
self.criterion = nn.KLDivLoss(size_average=False) # KL距离损失
self.padding_idx = padding_idx
self.confidence = 1.0 - smoothing
self.smoothing = smoothing
self.size = size
self.true_dist = None
def forward(self, predict, target):
assert predict.size(1) == self.size
true_dist = predict.data.clone()
true_dist.fill_(self.smoothing / (self.size - 2))
true_dist.scatter_(1, target.data.unsqueeze(1), self.confidence)
true_dist[:, self.padding_idx] = 0
mask = torch.nonzero(target.data == self.padding_idx)
if mask.dim() > 0:
true_dist.index_fill_(0, mask.squeeze(), 0.0)
self.true_dist = true_dist
criterion_result = self.criterion(predict, Variable(true_dist, requires_grad=False))
print("CriterionWithLabelSmoothing---->predict.shape = {0}----true_dist.shape = {1}----criterion_result = {2}".format(predict.shape, true_dist.shape, criterion_result))
return criterion_result
# # 测试标签平滑损失函数
# crit = CriterionWithLabelSmoothing(size=5, padding_idx=0, smoothing=0.5)
# predict = Variable(torch.FloatTensor([[0, 0.2, 0.7, 0.1, 0], [0, 0.2, 0.7, 0.1, 0], [0, 0.2, 0.7, 0.1, 0]])) # 假定一个任意的模型最后Softmax输出预测结果
# target = Variable(torch.LongTensor([2, 1, 0])) # 标签的表示值是0,1,2
# crit(predict, target) # 将predict, target传入到对象中
# plt.imshow(crit.true_dist)
# 6 损失计算工具包, 该工具能够进行损失的计算, 损失的计算方法可以认为是交叉熵损失函数.
class SimpleLossCompute:
def __init__(self, generator, criterion, opt=None):
self.generator = generator
self.criterion = criterion
self.opt = opt
def __call__(self, x, y, norm):
x = self.generator(x)
loss = self.criterion(x.contiguous().view(-1, x.size(-1)), y.contiguous().view(-1)) / norm
loss.backward()
if self.opt is not None:
self.opt.step()
self.opt.optimizer.zero_grad()
return loss.data * norm
# 7 模型单轮训练工具包run_epoch, 该工具将对模型使用给定的损失函数计算方法进行单轮参数更新.并打印每轮参数更新的损失结果.
def run_epoch(data_iter, model, loss_compute):
epoch_start_time = time.time()
total_tokens = 0
total_loss = 0
tokens = 0
for batch_index, batch in enumerate(data_iter):
batch_start_time = time.time()
print("run_epoch---->batch.ntokens = {0}".format(batch.ntokens))
out = model.forward(batch.src, batch.trg, batch.src_mask, batch.trg_mask)
loss = loss_compute(out, batch.trg_y, batch.ntokens)
total_loss += loss
total_tokens += batch.ntokens
tokens += batch.ntokens
batch_end_time = time.time()
timeused_of_this_batch = batch_end_time - batch_start_time
print("run_epoch---->batch_index = %d----Loss = %f----batch.ntokens = %f----batch average Loss = %f----当前batch所用时间 = %f 秒\n\n" % (batch_index, loss, int(batch.ntokens), loss / batch.ntokens, timeused_of_this_batch))
tokens = 0
avg_loss_of_this_epoch = total_loss / total_tokens
epoch_end_time = time.time()
timeused_of_this_epoch = epoch_end_time - epoch_start_time
print("run_epoch---->avg_loss_of_this_epoch = %f----当前epoch所用时间 = %f 秒" % (avg_loss_of_this_epoch, timeused_of_this_epoch))
return avg_loss_of_this_epoch
# 8 贪婪解码(贪心算法)的方式是每次预测都选择概率最大的结果作为输出, 它不一定能获得全局最优性, 但却拥有最高的执行效率.
def greedy_decode(model, source_tensor, source_mask, max_len, start_symbol):
memory = model.encode(source_tensor, source_mask)
print("greedy_decode---->start_symbol = {0}".format(start_symbol))
target_tensor = torch.ones(1, 1).fill_(start_symbol).type_as(source_tensor.data)
print("greedy_decode---->target_tensor = {0}".format(target_tensor))
for i in range(max_len - 1):
out = model.decode(target_tensor=Variable(target_tensor), memory=memory, source_mask=source_mask, target_mask=Variable(subsequent_mask(target_tensor.size(1)).type_as(source_tensor.data)))
prob = model.generator(out[:, -1])
_, next_word = torch.max(prob, dim=1)
next_word = next_word.data[0]
target_tensor = torch.cat([target_tensor, torch.ones(1, 1).type_as(source_tensor.data).fill_(next_word)], dim=1)
print("greedy_decode---->target_tensor = {0}".format(target_tensor))
return target_tensor
十六、函数分析
1、生成掩码张量的代码分析
向后遮掩的掩码张量函数: subsequent_mask
- 它的输入是size, 代表掩码张量的大小.
- 它的输出是一个最后两维形成1方阵的下三角阵
import torch #
import numpy as np
def subsequent_mask(size):
attn_shape = (1, size, size) # 定义掩码张量的形状【参数size是掩码张量最后两个维度的大小, attn_shape的最后两维形成一个方阵】
ones_matrix = np.ones(attn_shape)
print("ones_matrix = \n{0}".format(ones_matrix)) # 构建一个全1的张量
subsequent_mask = np.triu(ones_matrix, k=1).astype('uint8') # 使用np.triu形成上三角阵, 最后为了节约空间,再使其中的数据类型变为无符号8位整形unit8
print("subsequent_mask = \n{0}".format(subsequent_mask))
subsequent_mask_inverse = 1- subsequent_mask
print("subsequent_mask_inverse = \n{0}".format(subsequent_mask_inverse))
return torch.from_numpy(subsequent_mask_inverse) # 将numpy类型转化为torch中的tensor, 内部做一个1 - 的操作(其实是做了一个三角阵的反转, subsequent_mask中的每个元素都会被1减; 如果是0, subsequent_mask中的该位置由0变成1; 如果是1, subsequent_mask中的该位置由1变成0)
# 测试:生成20×20的掩码张量
size = 20 # 设置生成的掩码张量的最后两维的大小
sm = subsequent_mask(size)
print("sm = \n{0}".format(sm))
plt.figure(figsize=(5, 5))
plt.imshow(sm[0])
打印结果:
ones_matrix =
[[[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]]]
subsequent_mask =
[[[0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
[0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
[0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
[0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
[0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
[0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
[0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1]
[0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1]
[0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1]
[0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1]
[0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1]
[0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1]
[0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]]
subsequent_mask_inverse =
[[[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0]
[1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0]
[1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0]
[1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0]
[1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0]
[1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0]
[1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]]]
sm =
tensor([[[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]],
dtype=torch.uint8)
- 通过观察可视化方阵, 黄色是1的部分, 这里代表被遮掩, 紫色代表没有被遮掩的信息,
- 横坐标代表目标词汇的位置, 纵坐标代表可查看的位置;
- 在横坐标0的位置向纵坐标望过去都是黄色的, 都被遮住了,在横坐标1的位置向纵坐标望过去还是黄色, 说明第一次词还没有产生, 在横坐标2的位置向纵坐标望过去, 就能看到纵坐标位置1代表的第一个词, 其他位置看不到, 以此类推.
2、tensor.masked_fill函数
import torch
input = torch.randn(5, 5)
mask = torch.triu(torch.ones((5, 5)))
input_mask = input.masked_fill(mask == 0, 8)
print("input = {0}".format(input))
print("mask = {0}".format(mask))
print("input_mask = {0}".format(input_mask))
打印结果:
input = tensor(
[[-1.7438, -0.2589, 0.4346, -0.5157, 1.1203],
[ 0.4684, 0.0524, -0.8020, -1.1879, -0.1790],
[-2.0798, 0.5168, 0.1064, -0.5037, -1.5372],
[ 1.3878, -1.0330, 0.4094, -1.4374, -0.0788],
[ 0.7921, 0.4394, 0.5511, -0.6117, 1.0988]]
)
mask = tensor(
[[1., 1., 1., 1., 1.],
[0., 1., 1., 1., 1.],
[0., 0., 1., 1., 1.],
[0., 0., 0., 1., 1.],
[0., 0., 0., 0., 1.]]
)
input_mask = tensor(
[[-1.7438, -0.2589, 0.4346, -0.5157, 1.1203],
[ 8.0000, 0.0524, -0.8020, -1.1879, -0.1790],
[ 8.0000, 8.0000, 0.1064, -0.5037, -1.5372],
[ 8.0000, 8.0000, 8.0000, -1.4374, -0.0788],
[ 8.0000, 8.0000, 8.0000, 8.0000, 1.0988]]
)
参考资料:
Transformer一统江湖:自然语言处理三大特征抽取器比较
The Transformer Family
The Illustrated Transformer
The Annotated Transformer
A Deep Dive Into the Transformer Architecture – The Development of Transformer Models
Transformer图解
Transformer代码阅读
Transformer: A Novel Neural Network Architecture for Language Understanding
图解Transformer(完整版)
NLP 中的Mask全解
Talk to Transformer
Transformer的pytorch实现
基于pytorch的transformer代码实现(包含Batch Normalization,Layer normalization,Mask等讲述)