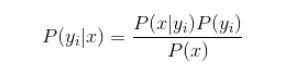朴素贝叶斯算法原理讲解

朴素贝叶斯算法原理讲解

1 算法抽象性解释

NaïveBayes算法，又叫朴素贝叶斯算法，是基于贝叶斯定理与特征条件独立假设的分类方法。

名称由来：朴素，即特征条ming件独立；贝叶斯：基于贝叶斯定理。所谓朴素，就是在整个形式化过程中只做最原始的假设。

朴素贝叶斯是贝叶斯决策理论的一部分，关于贝叶斯决策理论解释如下：

实例1：

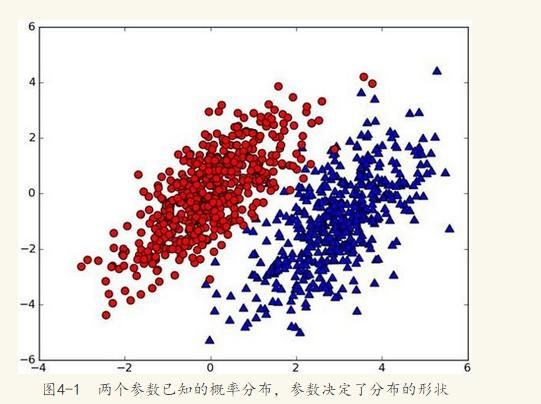
假设有一个数据集，由两类组成（简化问题），对于每个样本分类都已明确，数据分布如下图：

现在出现一个新的点new_point(x,y)，其分类未知，可用p1(x,y)表示数据点(x,y)属于红色一类的概率，同时也可以用p2(x,y)表示数据点(x,y)属于蓝色一类的概率。那么到底把new_point归在哪一类呢？

规则如下：

如果p1(x,y) > p2(x,y)，则(x,y)为红色一类。

如果p1(x,y) < p2(x,y)，则(x,y)为蓝色一类。

即选择概率高的一类作为new_point的分类。这就是贝叶斯决策理论的核心思想，即选择具有最高概率的决策。

若用条件概率的方式定义在这一贝叶斯分类准则，即为：

如果p(red|x,y) > p(blue|x,y), 则(x,y)属于红色一类。

如果p(red|x,y) < p(blue|x,y), 则(x,y)属于蓝色一类。

也就是说，当一个新的点需要分类时，我们仅需要计算这个点的

max(p(c1 | x,y)，p(c2 | x,y)，p(c3 | x,y)…p(cn| x,y))其对应的最大概率标签，就是这个新的点所属的类。

关键问题在于，对于分类i如何求解p(ci | x,y)？这就是贝叶斯公式：

实例2：

实例1借助的红色、蓝色分类是二维情况，接下来将要利用多维的说法来理解上述公式转化的重要性：判断一条微信朋友圈是不是广告？

前置条件：我们已经拥有了一个平日广大用户的朋友圈内容库，这些朋友圈当中，如果真的是在做广告的，会被“热心网友”打上“广告”的标签，我们要做的是把所有内容分成一个一个词，每个词对应一个维度，构建一个高维度空间。

当出现一条新的朋友圈new_post，我们将其分词，然后投放到朋友圈词库空间里。

这里的X表示多个特征（词）x1,x2,x3…组成的特征向量。

p(ad|x)表示：已知朋友圈内容而这条朋友圈是广告的概率

利用贝叶斯公式，进行转换：

p(ad|X) = p(X|ad)p(ad) / p(X)

p(not-ad|X)=p(X|not-ad)p(not-ad)/p(X)

比较上面两个概率的大小，如果p(ad|X)>not-ad|X)，则这条朋友圈被划分为广告，反之不是广告。

问题到这里，实际上已经转换为数学问题了，由接下来的公式推导进一步讲解

2 公式推导

1.设
$$x=a_1,a_2,\dots ，a_m$$
为一个待分类项，而每个a为x的一个特征属性

2.有类别集合
$$C=y_1,y_2,\dots ，y_n$$
3.计算
$$P(y_1|x),P(y_2|x),\dots ，P(y_n|x)$$
4.如果
$$P(y_k|x)=maxP(y_1|x),P(y_2|x),\dots ，P(y_n|x)$$
则
$$x\in y_k$$
那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做：

1、找到一个已知分类的待分类项集合，这个集合叫做训练样本集。
2、统计得到在各类别下各个特征属性的条件概率估计,即先验概率。
3、如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：

因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：

这里要引入朴素贝叶斯假设了。如果认为每个词都是独立的特征，那么朋友圈内容向量可以展开为分词(x1,x2,x3…xn)，因此有了下面的公式推导：

P(ad|X) = p(X|ad)p(ad) = p(x1, x2, x3, x4…xn | ad) p(ad)

假设所有词相互条件独立，则进一步拆分：
P(ad|X) = p(x1|ad)p(x2|ad)p(x3|ad)…p(xn|ad) p(ad)

虽然现实中，一条朋友圈内容中，相互之间的词不会是相对独立的，因为我们的自然语言是讲究上下文的╮(╯▽╰)╭，不过这也是朴素贝叶斯的朴素所在，简单的看待问题。

3 算法具体流程总结

(1) 对于给定的训练数据集，首先是基于特征条件独立假设学习输入输出的联合概率分布(此处的联合概率其实就是先验概率与条件概率的乘积)

(2) 然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y

朴素贝叶斯实现简单，学习与预测的效率都很高，是一种常用的方法。