cs224w（图机器学习）2021冬季课程学习笔记12 Knowledge Graph Embeddings

诸神缄默不语-个人CSDN博文目录
cs224w（图机器学习）2021冬季课程学习笔记集合

VX号“PolarisRisingWar”可直接搜索添加作者好友讨论。

更新日志：
2021.11.16 删除PPT链接，美化公式排版

YouTube 视频观看地址1 视频观看地址2 视频观看地址3

---

本章主要内容：
本章首先介绍了 异质图heterogeneous graph 和 relational GCN (RGCN)。
接下来介绍了 知识图谱补全knowledge graph completion 任务，以及通过图嵌入方式的四种实现方式及其对关系表示的限制：TransE，TransR，DistMult，ComplEx。

---

1. Heterogeneous Graphs and Relational GCN (RGCN)

1. 本节课任务：
   之前课程的内容都囿于一种边类型，本节课拓展到有向、多边类型的图（即异质图）上。
   介绍RGCN，知识图谱，知识图谱补全任务的表示方法。
   图的节点和边都可以是异质的
2. 异质图：
   节点集 $V$，节点 $v_i$
   边集 $E$，边 $(v_i,r,v_j)\in E$
   节点类型 $T(v_i)$
   边类型集合 $R$，边类型 $r$
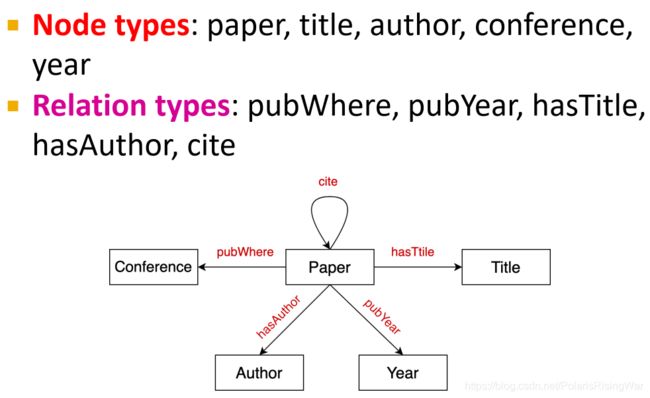
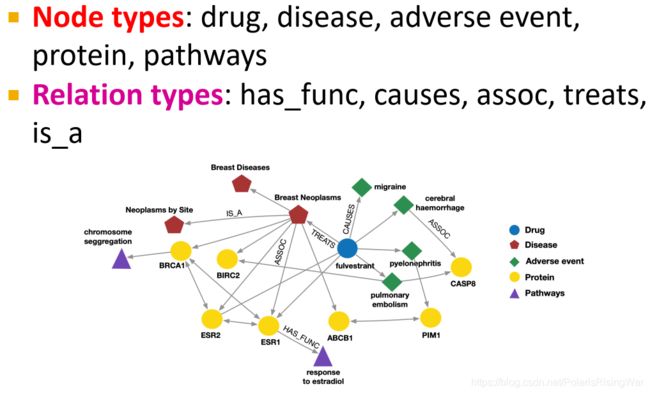
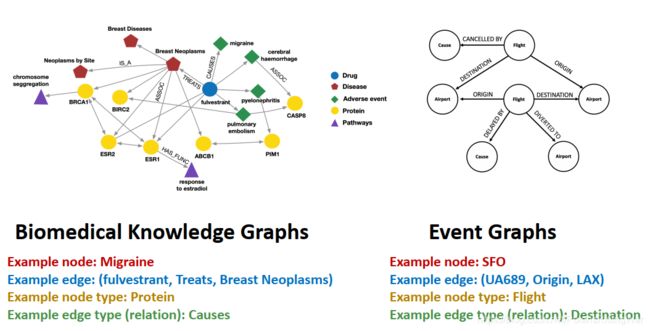
3. 异质图举例：生物医学知识图谱或事件图
4. Relational GCN¹
   将GCN²拓展到异质图上
   1. 从只有一种边类型的有向图开始：通过GCN学习节点A的表示向量，即沿其入边形成的计算图进行信息传播（message + aggregation）。
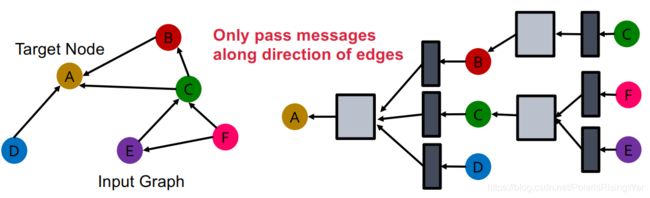
   2. 对于有多种边类型的情况：在信息转换时，对不同的边类型使用不同的权重 $W$
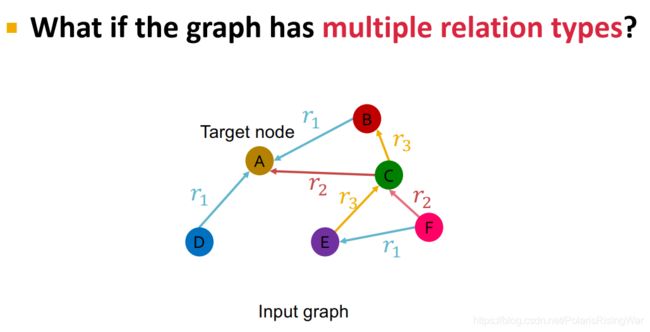
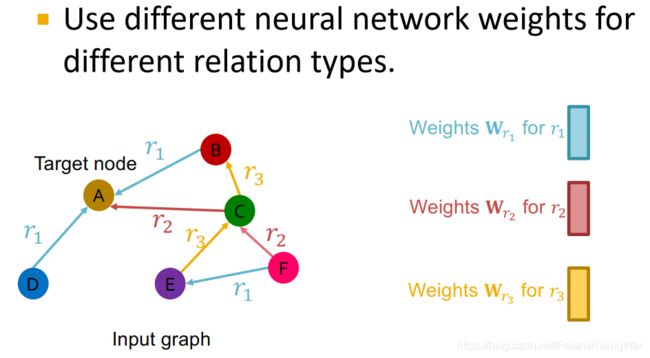
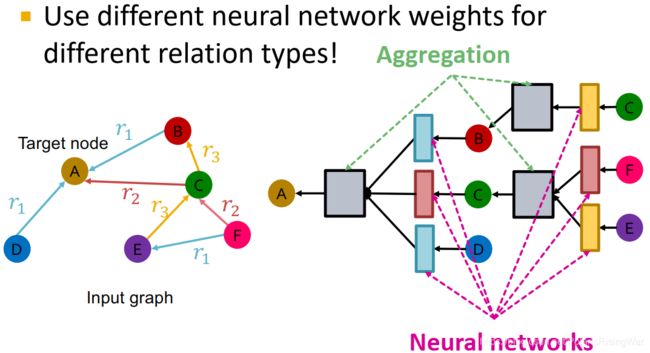
   3. Relation GCN定义³
      
      公式： ${\mathbf{h}}_v^{(l+1)}=\sigma \left(\sum _{r\in R}\sum _{u\in N_v^r}\frac{1}{c_{v,r}}{\mathbf{W}}_r^{(l)}{\mathbf{h}}_u^{(l)}+{\mathbf{W}}_r^{(0)}{\mathbf{h}}_v^{(l)}\right)$
      （$c_{v,r}=|N_v^r|$ 用节点in-degree进行归一化）
      
      message：
       对特定关系的邻居：${\mathbf{m}}_{u,r}^{(l)}=\frac{1}{c_{v,r}}{\mathbf{W}}_r^{(l)}{\mathbf{h}}_u^{(l)}$
       自环：${\mathbf{m}}_v^{(l)}={\mathbf{W}}_r^{(0)}{\mathbf{h}}_v^{(l)}$
      aggregation：加总邻居和自环信息，应用激活函数：${\mathbf{h}}_v^{(l+1)}=\sigma \left(\text{Sum}(\{{\mathbf{m}}_{u,r}^{(l)},u\in \{N(v)\}\cup \{v\}\})\right)$
5. RGCN的scalability
   每种关系都需要 $L$（层数）个权重矩阵：${\mathbf{W}}_r^{(1)}$，${\mathbf{W}}_r^{(2)}$ … ${\mathbf{W}}_r^{(L)}$
   每个权重矩阵的尺寸为 $d^{(l+1)}\times d^{(l)}$（$d^{(l)}$ 是第 $l$ 层的隐嵌入维度）
   
   参数量随关系类数迅速增长，易产生过拟合问题
   2种规则化权重矩阵的方法：block diagonal matrices 和 basis/dictionary learning
   1. block diagonal matrices
      使权重矩阵变稀疏，减少非0元素数量。
      做法就是如图所示，让权重矩阵成为这样对角块的形式。如果用B个低维矩阵，参数量就会从 $d^{(l+1)}\times d^{(l)}$ 减少到 $B\times \frac{d^{(l+1)}}{B}\times \frac{d^{(l)}}{B}$。
      这种做法的限制在于，这样就只有相邻神经元/嵌入维度可以通过权重矩阵交互了⁴。要解决这一限制，需要多加几层神经网络，或者用不同的block结构，才能让不在一个block内的维度互相交流。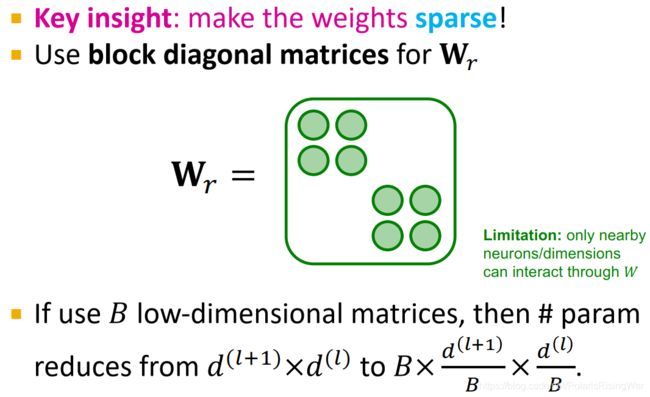
   2. basis learning
      在不同关系之间共享权重参数。
      做法：将特定关系的权重矩阵表示为 基变换basis transformations 的 线性组合linear combination 的形式：${\mathbf{W}}_r={\sum }_{b=1}^B{a}_{rb}\cdot {\mathbf{V}}_b$（${\mathbf{V}}_b$ 在关系间共享）
      ${\mathbf{V}}_b$ 是 basis matrices 或 dictionary
      $a_{rb}$ 是 ${\mathbf{V}}_b$ 的 importance weight
      这样我们对每个关系就只需要学习 $\{a_{rb}{\}}_{b=1}^B$ 这 B 个标量了
6. 示例
   1. 实体/节点分类
      目标：预测节点标签。
      RGCN使用最后一层产生的表示向量。
      举例：k-way分类任务，使用节点 $A$ 最后一层（prediction head）的输出 ${\mathbf{h}}_A^{(L)}\in {\mathbb{R}}^k$（比如可能是经softmax输出），每个元素表示对应节点属于对应类的概率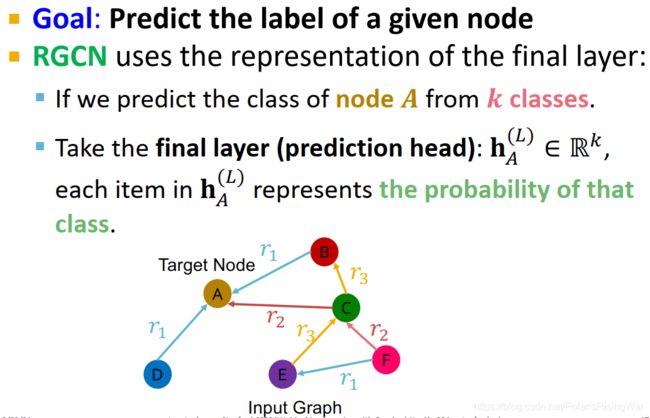
   2. 链接预测
      在异质图中，将每种关系对应的边都分成 training message edges, training supervision edges, validation edges, test edges 四类⁵（切分每种关系所组成的同质图）。
      这么分是因为有些关系类型的边可能很少，如果全部混在一起四分的话可能有的就分不到（比如分不到验证集里……之类的）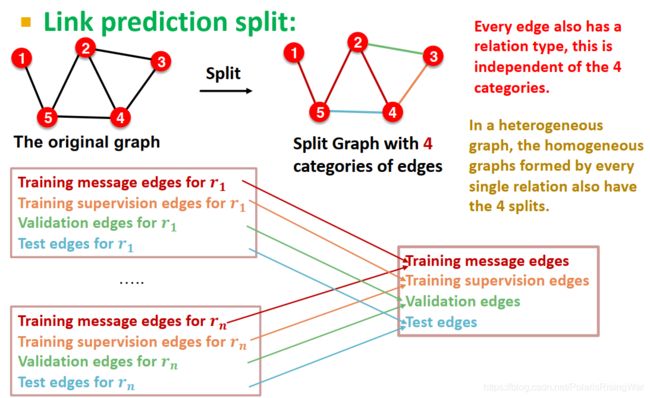
      RGCN在链接预测任务上的应用：
      假定 $(E,r_3,A)$ 是 training supervision edge，则其他边都是 training message edges。
      用RGCN给 $(E,r_3,A)$ 打分：
       首先得到最后一层节点 $E$ 和节点 $A$ 的输出向量：${\mathbf{h}}_E^{(L)}$ and ${\mathbf{h}}_A^{(L)}\in {\mathbb{R}}^d$
       然后应用 relation-specific 的打分函数 $f_r:{\mathbb{R}}^d\times {\mathbb{R}}^d\to \mathbb{R}$
       （举例：$f_{r_1}({\mathbf{h}}_E,{\mathbf{h}}_A)={\mathbf{h}}_E^T{\mathbf{W}}_{r_1}{\mathbf{h}}_A,{\mathbf{W}}_{r_1}\in {\mathbb{R}}^{d\times d}$ ⁶）
      1. 训练阶段：用 training message edges 预测 training supervision edges
         1. 用RGCN给 training supervision edge $(E,r_3,A)$ 打分。
         2. 通过 扰乱perturb supervision edge 得到 negative edge⁷：corrupt $(E,r_3,A)$ 的尾节点，举例得到 $(E,r_3,B)$。
            注意 negative edge 不能属于 training message edges 或 training supervision edges。
         3. 用GNN模型给 negative edge 打分
         4. 优化交叉熵⁸ 损失函数，使 training supervision edge 上得分最大，negative edge 上得分最低：
            $\ell =-\log \sigma \left(f_{r_3}(h_E,h_A))-\log (1-\sigma (f_{r_3}(h_E,h_B))\right)$
            （$\sigma$ 是sigmoid函数）
            
      2. 验证阶段（测试阶段类似）：
         用 training message edges 和 training supervision edges 预测 validation edges：$(E,r_3,D)$ 的得分应该比所有 negative edges 的得分更高
         negative edges：尾节点不在 training message edges 和 training supervision edges 中的以 $E$ 为头节点、$r_3$ 为关系的边（举例：$(E,r_3,B)$ ）
         
         具体步骤：
         1. 计算 $(E,r_3,D)$ 的得分
         2. 计算所有 negative edges：$\{(E,r_3,v)|v\in \{B,F\}\}$ 的得分
         3. 获得 $(E,r_3,D)$ 的 排名 ranking RK
         4. 计算指标：
            1. Hits@k: $\text{RK}\le k$ 的次数，越高越好
            2. Reciprocal Rank：$\frac{1}{\text{RK}}$，越高越好
7. 总结
   1. Relational GCN：用于异质图的图神经网络模型
   2. 可用于实体分类和链接预测任务
   3. 类似思想可以扩展到其他RGNN模型上（如RGraphSAGE，RGAT等）

2. Knowledge Graphs: KG Completion with Embeddings

1. 知识图谱 Knowledge Graphs (KG)
   以图形式呈现的知识
   捕获实体entity（节点）、类型（节点标签）、关系relationship（边）
   一种异质图实例
2. 示例
   1. bibliographic networks
      bibliographic书目的；书籍解题的；著书目录的
      通过定义节点类型、关系类型及其之间的关系，得到如图所示的schema ⁹：
   2. bio knowledge graphs
      
      adverse event 不良反应
      pathway 总之是个专业术语，过程、反应之类的¹⁰
3. 知识图谱应用实例（就我本来想把这些介绍网址啥的列出来的，但我最近不能上某些网站了，而且我又现在不用，就先直接截图了。以后有缘可以搞一下。如果真的有读者看到这里而且有这样需求的话也可以戳我催更）
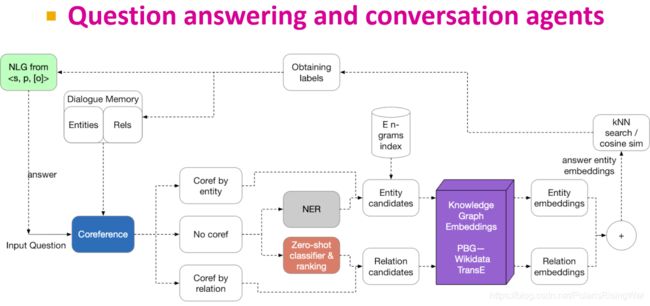
4. 公开可用的知识图谱有：FreeBase, Wikidata, Dbpedia, YAGO, NELL, etc.
   这些知识图谱的共同特点是：大，不完整（缺少很多真实边）
   对于一个大型KG，几乎不可能遍历所有可能存在的事实，因此需要预测可能存在却缺失的边
5. 举例：Freebase¹¹
   大量信息缺失
   有 complete 的子集供研究KG模型

3. Knowledge Graph Completion: TransE, TransR, DistMult, ComplEx

1. 知识图谱补全 KG Completion Task
   已知 (head, relation)，预测 tails（注意，这跟链接预测任务有区别，链接预测任务是啥都不给，直接预测哪些链接最有可能出现）
   举例：已知（JK罗琳，作品流派），预测 tail “科幻小说”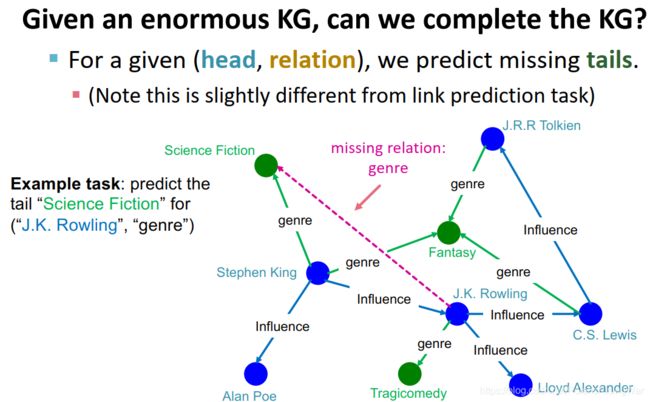

2. 在本节课中使用 shallow encoding¹² 的方式来进行图表示学习，也就是用固定向量表示图数据
   （虽然这里不用GNN，但是如果愿意的话也可以用）

3. 知识图谱表示
   边被表示为三元组的形式：$(h,r,t)$  head, relation, tail
   将实体和边表示到嵌入域/表示域（${\mathbb{R}}^d$）中（使用shallow embeddings）
   
   给出一个真实的三元组 $(h,r,t)$，目标是对 $(h,r)$ 的嵌入应靠近 $t$ 的嵌入
   以下介绍如何嵌入 $(h,r)$ 、如何定义相似性

4. TransE¹³
   （translate embeddings）
   给出三元组 $(h,r,t)$，将实体和关系都映射到 ${\mathbb{R}}^d$ 上（用粗体表示嵌入向量，普通字母表示原KG中的实体或关系），使三元组为真时 $\mathbf{h}+\mathbf{r}\approx \mathbf{t}$，反之 $\mathbf{h}+\mathbf{r}\ne \mathbf{t}$
   scoring function：$f_r(h,t)=-||\mathbf{h}+\mathbf{r}-\mathbf{t}||$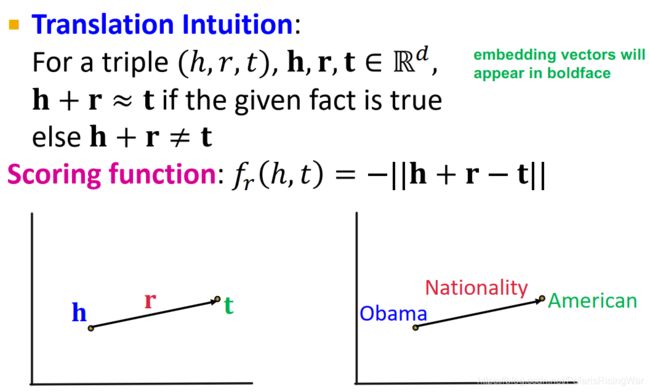

5. TransE的算法
   简单来说，我没看懂。大致来讲过程是这样的：
   
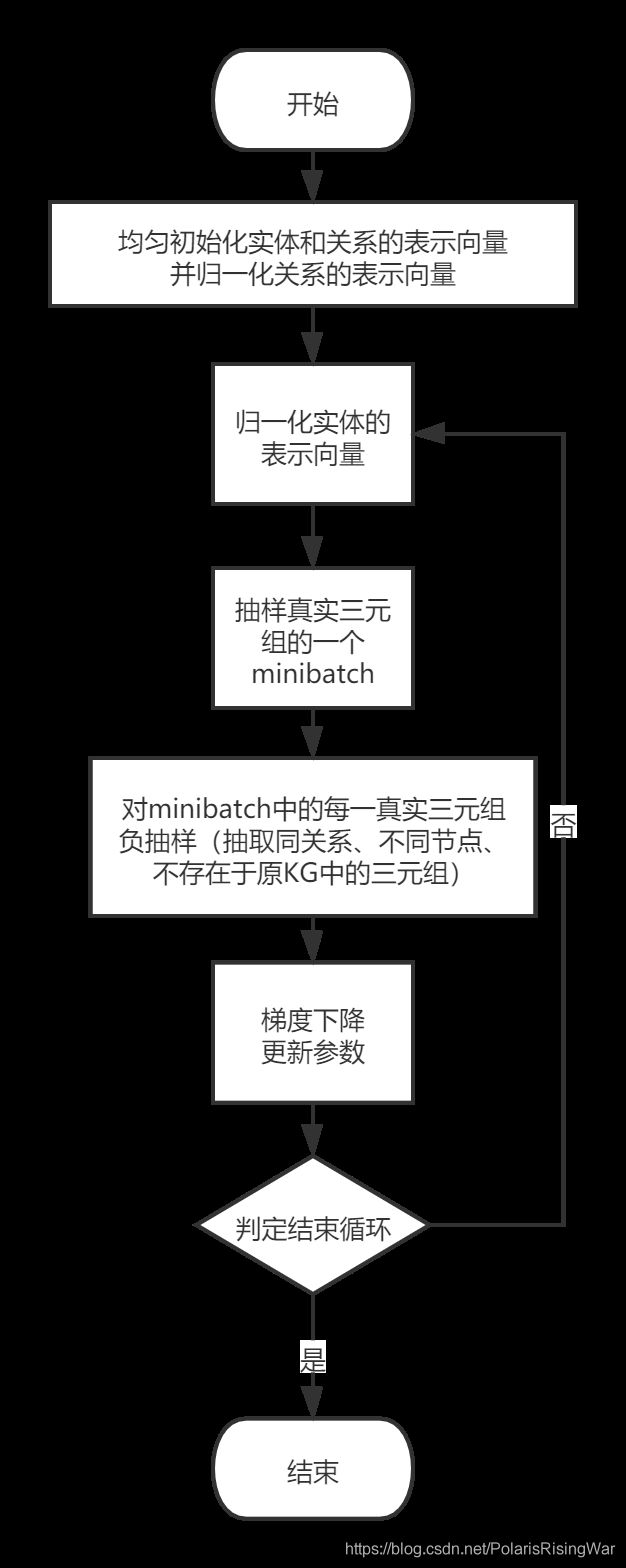
   初始化部分我没看懂，以后再研究。
   更新参数时使用的是 contrastive loss，总之大意就是最小化真三元组的距离（也就是最大化真三元组的score或相似性）、最大化假三元组的距离

6. KG中关系的模式 Connectivity Patterns in KG
   在KG中，关系可能有多种属性，我们接下来就要探讨KG嵌入方法（如TransE等）能否建模、区分开这些关系模式：

   1. symmetric relations（如室友关系）
      $r(h,t)\Rightarrow r(t,h)$
   2. antisymmetric relations（如上位词关系）
      $r(h,t)\Rightarrow \neg r(t,h)$
   3. inverse relations（如导师-学生关系）
      $r_2(h,t)\Rightarrow r_1(t,h)$
   4. composition (transitive) relations（如母亲-姐姐-姨母关系）
      $r_1(x,y)\wedge r_2(y,z)\Rightarrow r_3(x,z)$
   5. 1-to-N relations（如 的学生 关系）
      $r(h,t_1),r(h,t_2),...,r(h,t_n)$ 同时为真

7. TransE：Antisymmetric Relations $✓$
   $\mathbf{h}+\mathbf{r}=\mathbf{t}$，但 $\mathbf{t}+\mathbf{r}\ne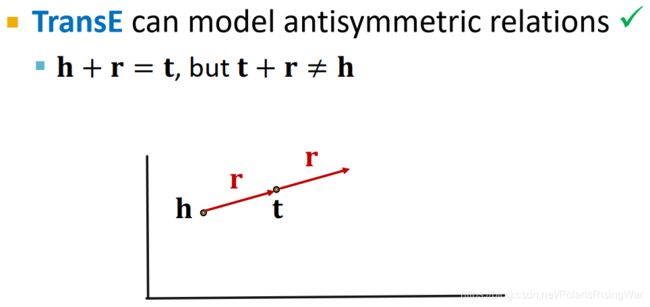 \mathbf{h}$

8. TransE：Inverse Relations $✓$
   $\mathbf{h}+{\mathbf{r}}_2=\mathbf{t}$，设置 ${\mathbf{r}}_2=-{\mathbf{r}}_1$ 即可实现 $\mathbf{t}+{\mathbf{r}}_1=\mathbf{h}$

9. TransE：Composition $✓$
   已知 $\mathbf{x}+{\mathbf{r}}_1=\mathbf{y}$ ①，$\mathbf{y}+{\mathbf{r}}_2=\mathbf{z}$ ②
   则若 ${\mathbf{r}}_3={\mathbf{r}}_1+{\mathbf{r}}_2$，将①②相加，消项后就能得到 $\mathbf{x}+{\mathbf{r}}_3=\mathbf{z}$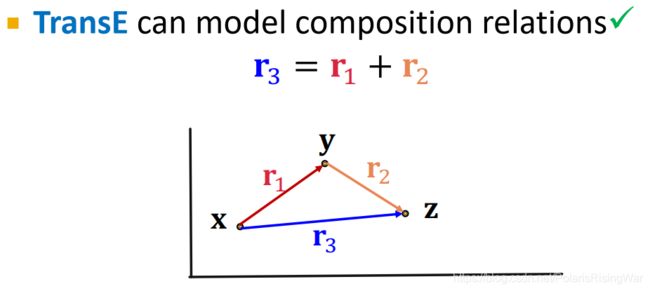

10. TransE：Symmetric Relations $✖$
    欲使 $||\mathbf{h}+\mathbf{r}-\mathbf{t}||=0$ 和 $||\mathbf{t}+\mathbf{r}-\mathbf{h}||=0$ 同时成立，需 $\mathbf{r}=0$ 且 $\mathbf{h}=\mathbf{t}$，但这样把两个实体嵌入到同一点上就没有意义了，所以是不行的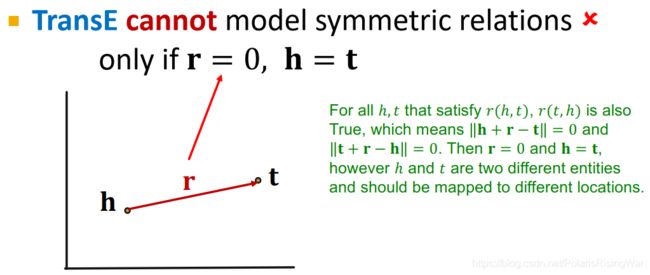

11. TransE：1-to-N Relations $✖$
    欲使 $||\mathbf{h}+\mathbf{r}-{\mathbf{t}}_1||=0$ 和 $||\mathbf{h}+\mathbf{r}-{\mathbf{t}}_2||=0$ 同时成立，需 ${\mathbf{t}}_1={\mathbf{t}}_2$，但这样把两个实体嵌入到同一点上就没有意义了，所以是不行的

12. TransR¹⁴
    将实体映射为实体空间 ${\mathbb{R}}^d$ 上的向量，关系映射为关系空间上的向量 $\mathbf{r}\in {\mathbb{R}}^k$，且有 relation-specific 的 projection matrix ${\mathbf{M}}_r\in {\mathbb{R}}^{k\times d}$
    用 projection matrix 将实体从实体域投影到空间域上：${\mathbf{h}}_{\perp }={\mathbf{M}}_r\mathbf{h}$，${\mathbf{t}}_{\perp }={\mathbf{M}}_r\mathbf{t}$
    scoring function：$f_r(h,t)=-||{\mathbf{h}}_{\perp }+\mathbf{r}-{\mathbf{t}}_{\perp }||$

13. TransR：Symmetric Relations $✓$
    使 $\mathbf{r}=0$，${\mathbf{h}}_{\perp }={\mathbf{M}}_r\mathbf{h}={\mathbf{M}}_r\mathbf{t}={\mathbf{t}}_{\perp }$，即可以使在实体域上不同的 $h$ 和 $t$ 可以在 $r$ 的关系域上相同。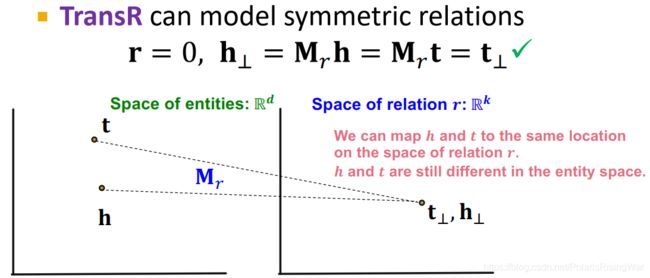

14. TransR：Antisymmetric Relations $✓$
    $\mathbf{r}\ne 0$，${\mathbf{M}}_r\mathbf{h}+\mathbf{r}={\mathbf{M}}_r\mathbf{t}$，则 ${\mathbf{M}}_r\mathbf{t}+\mathbf{r}\ne {\mathbf{M}}_r\mathbf{h}$，自然实现要求

15. TransR：1-to-N Relations $✓$
    可以通过学习合适的 ${\mathbf{M}}_r$ 使 ${\mathbf{t}}_{\perp }={\mathbf{M}}_r{\mathbf{t}}_1={\mathbf{M}}_r{\mathbf{t}}_2$，即在实体域中不同的 $t_1$ 和 $t_2$ 可以在 $r$ 的关系域上相同
    

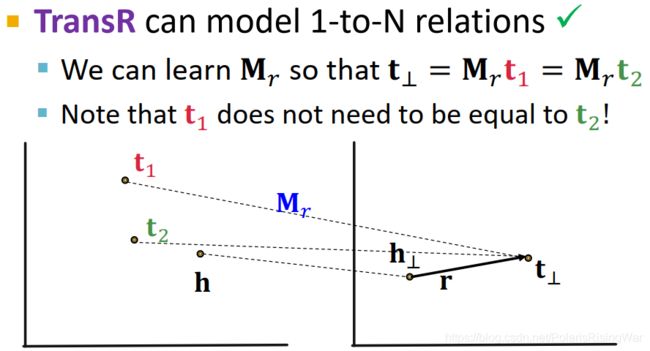
16. TransR：Inverse Relations $✓$
    使 ${\mathbf{r}}_2=-{\mathbf{r}}_1$，${\mathbf{M}}_{r_1}={\mathbf{M}}_{r_2}$
    就能使 ${\mathbf{M}}_{r_1}\mathbf{t}+{\mathbf{r}}_1={\mathbf{M}}_{r_1}\mathbf{h}$ 且 ${\mathbf{M}}_{r_2}\mathbf{h}+{\mathbf{r}}_2={\mathbf{M}}_{r_2}\mathbf{t}$
    

17. TransR：Composition Relations $✖$
    每个关系都有独立的空间域，不能直接自然组合¹⁵

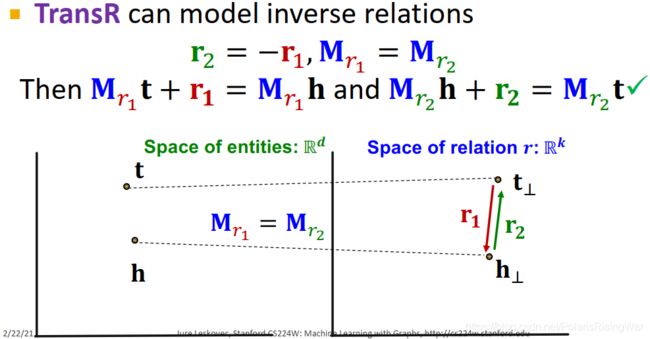
18. New Idea: Bilinear Modeling¹⁶
    在至今学习过的TransE和TransR中，scoring function $f_r(h,t)$ 都是L1或L2距离的相反数。另一种做法是选用 bilinear modeling¹⁶。
    DistMult¹⁷：实体和关系都表示为 ${\mathbb{R}}^k$ 的向量（在这一点上有点像TransE）
    score function：$f_r(h,t)=<\mathbf{h},\mathbf{r},\mathbf{t}>={\sum }_i{\mathbf{h}}_i\cdot {\mathbf{r}}_i\cdot {\mathbf{t}}_i$（点积）

19. DistMult
    score function 可以直觉地被视作 $\mathbf{h}\cdot \mathbf{r}$ 和 $\mathbf{t}$ 之间的 cosine similarity¹⁸
    即，使 $\mathbf{h}\cdot \mathbf{r}$ 和 $\mathbf{t}$ 同侧、靠近时，score 较高。
    

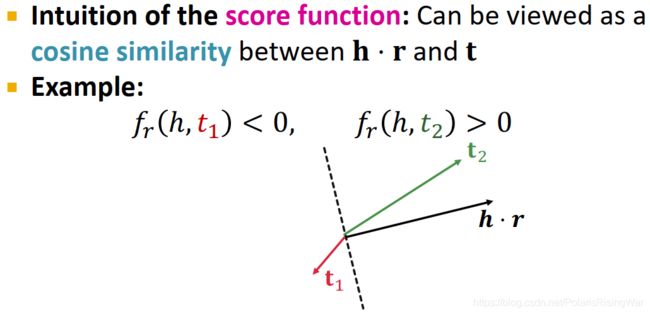
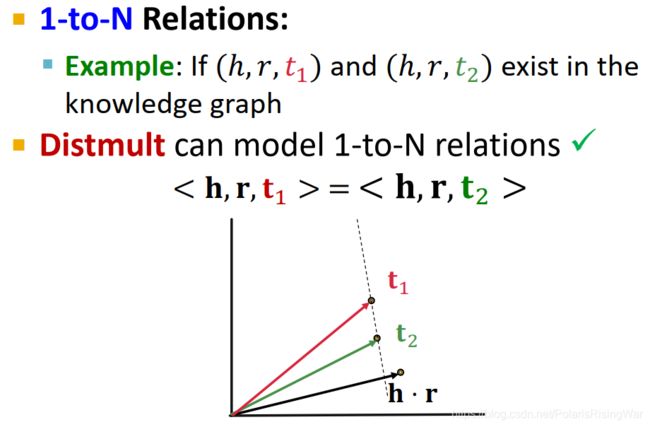
20. DistMult：1-to-N Relations $✓$
    当知识图谱中存在 $(h,r,t_1)$ 和 $(h,r,t_2)$ 时，如图所示，DistMult可以建模使 ${\mathbf{t}}_1$ 和 ${\mathbf{t}}_2$ 在 $\mathbf{h}\cdot \mathbf{r}$ 上的投影等长，即使二者与 $\mathbf{h}\cdot \mathbf{r}$ 的点积相等，即 $<\mathbf{h},\mathbf{r},{\mathbf{t}}_1>=<\mathbf{h},\mathbf{r},{\mathbf{t}}_2>$，符合要求
    

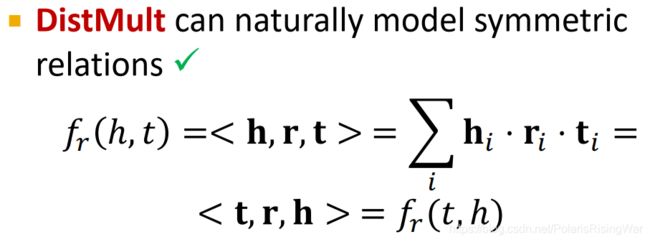
21. DistMult：Symmetric Relations $✓$
    DistMult天然建模symmetric relations：$f_r(h,t)=<\mathbf{h},\mathbf{r},\mathbf{t}>=\sum _i{\mathbf{h}}_i\cdot {\mathbf{r}}_i\cdot {\mathbf{t}}_i=<\mathbf{t},\mathbf{r},\mathbf{h}>=f_r(t,h)$（乘法交换律）
    

22. DistMult：Antisymmetric Relations $✖$
    $f_r(h,t)=<\mathbf{h},\mathbf{r},\mathbf{t}>=<\mathbf{t},\mathbf{r},\mathbf{h}>=f_r(t,h)$ 永远成立，不符要求
    

23. DistMult：Inverse Relations $✖$
    如果要建模inverse relations，即使：$f_{r_2}(h,t)=<\mathbf{h},{\mathbf{r}}_2,\mathbf{t}>=<\mathbf{t},{\mathbf{r}}_1,\mathbf{h}>=f_{r_2}(t,h)$
    必须使 ${\mathbf{r}}_2={\mathbf{r}}_1$，这显然是没有意义的
    

24. DistMult：Composition Relations $✖$
    DistMult对每个 (head,relation) 定义了一个超平面，对多跳关系产生的超平面的联合（如 $(r_1,r_2)$）无法用单一超平面（$r_3$）来表示。¹⁹
    

25. ComplEx²⁰
    基于DistMult，ComplEx在 复数向量域complex vector space ${\mathbb{C}}^k$ 中表示实体和关系。
    $\mathbf{u}=\mathbf{a}+\mathbf{b}i$（其中 $\mathbf{u}\in {\mathbb{C}}^k$，实部re $\mathbf{a}\in {\mathbb{R}}^k$，虚部im $\mathbf{b}\in {\mathbb{R}}^k$）
    $\overline{\mathbf{u}}=\mathbf{a}-\mathbf{b}i$（共轭）
    
    
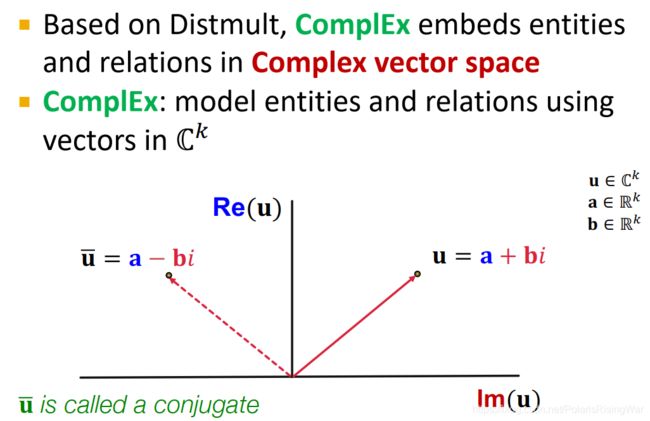
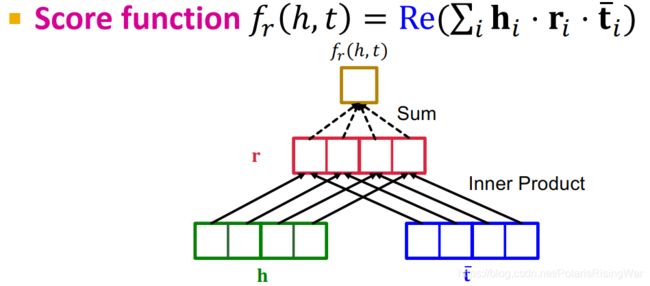
    score function：$f_r(h,t)=\text{Re}({\sum }_i{\mathbf{h}}_i\cdot {\mathbf{r}}_i\cdot {\overline{\mathbf{t}}}_i)$²¹
    

26. ComplEx：Antisymmetric Relations $✓$
    ComplEx可以建模使 $f_r(h,t)=\text{Re}({\sum }_i{\mathbf{h}}_i\cdot {\mathbf{r}}_i\cdot {\overline{\mathbf{t}}}_i)$ 与 $f_r(t,h)=\text{Re}({\sum }_i{\mathbf{t}}_i\cdot {\mathbf{r}}_i\cdot {\overline{\mathbf{h}}}_i)$ 不同，因为这一不对称建模使用的是复数共轭。
    

27. ComplEx：Symmetric Relations $✓$
    当 $\text{Im}(\mathbf{r})=0$ 时，$f_r(h,t)=\text{Re}({\sum }_i{\mathbf{h}}_i\cdot {\mathbf{r}}_i\cdot {\overline{\mathbf{t}}}_i)={\sum }_i\text{Re}({\mathbf{r}}_i\cdot {\mathbf{h}}_i\cdot {\overline{\mathbf{t}}}_i)={\sum }_i{\mathbf{r}}_i\cdot \text{Re}({\mathbf{h}}_i\cdot {\overline{\mathbf{t}}}_i)={\sum }_i{\mathbf{r}}_i\cdot \text{Re}({\overline{\mathbf{h}}}_i\cdot {\mathbf{t}}_i)={\sum }_i\text{Re}({\mathbf{r}}_i\cdot {\overline{\mathbf{h}}}_i\cdot {\mathbf{t}}_i)=f_r(t,h)$
    符合要求
    

28. ComplEx：Inverse Relations $✓$
    已知 ${\mathbf{r}}_2=\underset{\mathbf{r}}{\mathrm{argmax}}\text{Re}(<\mathbf{h},\mathbf{r},\overline{\mathbf{t}}>)$
    欲知 ${\mathbf{r}}_1=\underset{\mathbf{r}}{\mathrm{argmax}}\text{Re}(<\mathbf{t},\mathbf{r},\overline{\mathbf{h}}>)$
    当 ${\mathbf{r}}_1={\overline{\mathbf{r}}}_2$ 即 ${\mathbf{r}}_2$ 的共轭正是 ${\mathbf{r}}_1$ 时，满足要求。
    

29. ComplEx：Composition Relations $✖$ 1-to-N Relations $✓$
    和DistMult一样

30. 所有模型的表示能力对比：
    

31. 知识图谱嵌入问题的实践应用²²

    1. 不同知识图谱可能会有很不同的关系模式
    2. 因此没有适合所有KG的嵌入方法，可用上表来辅助选择
    3. 可以先试用TransE来迅速获得结果（如果目标KG没有过多symmetric relations的话）
    4. 然后再用更有表示能力的模型，如ComplEx或RotatE²²（复数域的TransE）等

32. 总结

    1. 链接预测或图补全任务是知识图谱领域的重要研究任务
    2. 介绍了不同嵌入域和不同表示能力的模型
       1. TransE
       2. TransR
       3. DistMult
       4. ComplEx

---

1. Schlichtkrull et al., Modeling Relational Data with Graph Convolutional Networks, ESWC 2018 ↩︎

2. 可参考我写的前几节课的笔记博文 ↩︎

3. 说起来这个RGCN是有自环的啊，但是前几节课我看GCN是没算自环的啊？所以到底要不要自环啊？ ↩︎

4. 其实我没太看懂这句话啥意思。
   很容易理解的是，就是这样的话，每次使用权重矩阵时，只有相邻嵌入（对角块同一行上非0元素索引对应的嵌入维度）能与权重矩阵的元素进行运算、学习（交互）。所以这又能咋样……这有啥不好之处吗？
   另外就是，说这个维度是神经元……虽然我想了一下好像按照神经网络的逻辑，就是神经元，但总感觉很奇怪……说起来GNN就是跟传统神经网络好不一样啊，真的可以套用吗？ ↩︎

5. 可参考我之前写的博文：cs224w（图机器学习）2021冬季课程学习笔记10 Applications of Graph Neural Networks ↩︎

6. 这个 $f$ 是 双线性型bilinear form¹⁶ ↩︎

7. 这个获得negative edges的方法是必须要改supervision edge来吗，还是别的任意一条在training message edge和training supervision edge中不存在的该关系对应的边都可以？改supervision edge的唯一方法是改destination节点吗？这部分我还没搞懂。
   我一开始还在考虑其他关系的边怎么处理，但是看到例子中存在其他关系的边也可以被认为是negative edges，大概就是不管其他关系了吧。
   我一开始另外也考虑了是否需要避开validation edge和test edge吗，但是我看例子里面就没管它们，所以应该不影响。 ↩︎

8. 交叉熵相关讲解可参考我之前写的博文：cs224w（图机器学习）2021冬季课程学习笔记7 Graph Neural Networks 1: GNN Model
   我看了一下这个公式，我能理解优化这个公式能达到所要求的效果，但是为什么就能这样搞？我就没搞懂。 ↩︎

9. 但其实就是我不太确定schema是不是就是这个东西 ↩︎

10. 毕竟不是我的学科领域，所以我就简单百度了一下，知道这是个专业术语就完了。欲了解详情可以百度。我给出的参考资料是这篇帖子：题外话——生物学中的pathway - 分子生物 - 生物化学 - 小木虫论坛-学术科研互动平台 ↩︎

11. slides中给出的参考文献：
    ①Paulheim, Heiko. “Knowledge graph refinement: A survey of approaches and evaluation methods.” Semantic web 8.3 (2017): 489-508.
    这一篇论文我没找到直接的PDF下载地址，就从道客巴巴上下了一个，放在了我自己的GitHub项目上：all-notes-in-one/Knowledge graph refinement.pdf at main · PolarisRisingWar/all-notes-in-one
    ②Min, Bonan, et al. “Distant supervision for relation extraction with an incomplete knowledge base.” Proceedings of the 2013 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. 2013. ↩︎

12. 可参考我之前写的博文：cs224w（图机器学习）2021冬季课程学习笔记3: Node Embeddings ↩︎

13. Bordes, et al., Translating embeddings for modeling multi-relational data, NeurIPS 2013 ↩︎

14. Lin, et al., Learning entity and relation embeddings for knowledge graph completion, AAAI 2015
    呃……但是这个AAAI的网址，不知道为什么我上不了，是因为墙？但是这个网站有什么好墙的？等我能使用特殊手段再研究吧，反正现在也不需要看这篇论文 ↩︎

15. 这个我也没看懂……各个关系向量不在一个空间，这个我就不太理解，它们不都是同一维度（${\mathbb{R}}^k$）上的向量吗？只因为投射矩阵M不同吗？
    就我能理解对于同一实体来说，不同的关系会将其映射到不同的位置上……但是，所以呢？
    slides上说是因为这个在x-y，y-z关系中的y所组成的流形（这又是个什么东西？）集合是高维的，无法用单一关系和关系矩阵来建模……啥意思？ ↩︎

16. 到底什么他妈的是双线性型？数学怎么就这么难啊？ ↩︎ ↩︎ ↩︎

17. Yang et al, Embedding Entities and Relations for Learning and Inference in Knowledge Bases, ICLR 2015 ↩︎

18. 就很明显是点积嘛。
    但我还是没搞懂这为啥就是余弦相似度了？就同质图那边讲相似性问题的时候我就没搞懂，点积和余弦相似度之间不是差个模长吗？模长呢？有说这几个向量的模长都是1吗还是咋整了？
    这种细节我寻思可能还是得看看相应的代码，看看相应的实践上的处理方式。假如我能看得懂的话，我再回来写解释。 ↩︎

19. 这他妈是什么东西啊，完全没看懂(〃＞皿＜)
    就是，硬要讲这个超平面的话，我能理解，就是与 $\mathbf{h}\mathbf{e}\mathbf{a}\mathbf{d}\cdot \mathbf{r}\mathbf{e}\mathbf{l}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}$ 相正交的那个超平面吧？
    然后两个超平面合起来不一定是一个超平面，就，这怎么合啊！
    然后我就没搞懂别的在说啥了。 ↩︎

20. Trouillon et al, Complex Embeddings for Simple Link Prediction, ICML 2016 ↩︎

21. 就，大概是囿于我复数知识的严重匮乏吧，ComplEx的自此以下所有公式我都没搞懂。
    就，复数的共轭和实部能干这么多事呢？？？这就是我的感觉。
    我看不懂，但我大受震撼。 ↩︎

22. Sun et al, RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space, ICLR 2019 ↩︎ ↩︎