基于改进人工蜂群算法的K均值聚类算法(Matlab代码实现)
欢迎来到本博客❤️❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
目录
1 概述
2 文献来源
3 运行结果
4 Matlab代码实现
1 概述
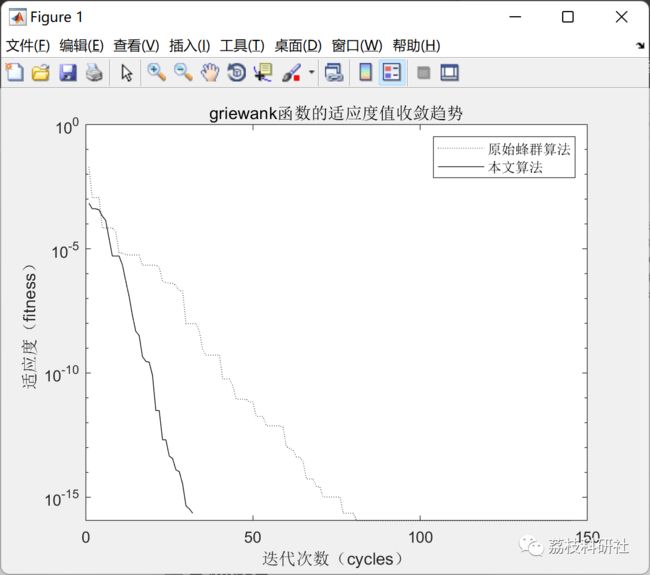
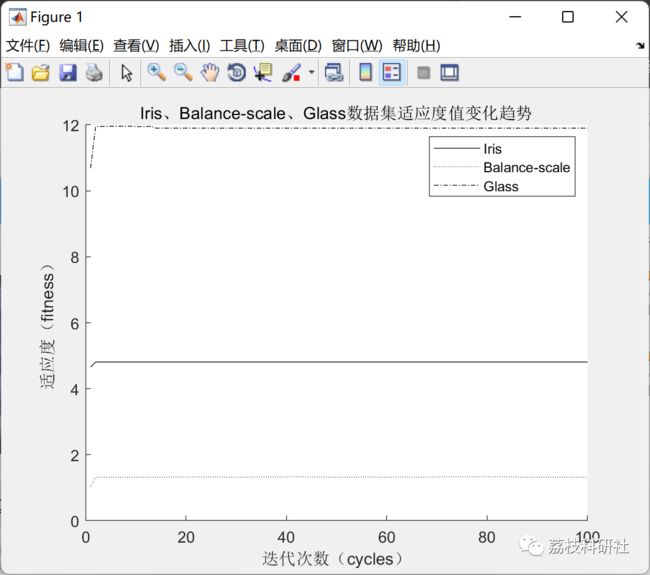
针对K均值聚类(KMC)算法全局搜索能力差、初始聚类中心选择敏感,以及原始人工蜂群(ABC)算法的初始化随机性﹑易早熟、后期收敛速度慢等问题,提出了一种改进人工蜂群算法( IABC)。该算法利用最大最小距离积方法初始化蜂群,构造出适应KMC算法的适应度函数以及一种基于全局引导的位置更新公式以提高迭代寻优过程的效率。将改进的人工蜂群算法与KMC算法结合提出IABC-Kmeans算法以改善聚类性能。通过Sphere 、Rastrigin、Rosenbrock 和Griewank 四个标准测试函数和UCI标准数据集上进行测试的仿真实验表明,IABC算法收敛速度快,克服了原始算法易陷入局部最优解的缺点; IABC-Kmeans算法则具有更好的聚类质量和综合性能。
2 文献来源
3 运行结果
部分代码:
function [Colony Obj Fit oBas]=GreedySelection(Colony1,Colony2,ObjEmp,ObjEmp2,FitEmp,FitEmp2,fbas,ABCOpts,i)
oBas=fbas;
Obj=ObjEmp;
Fit=FitEmp;
Colony=Colony1;
if (nargin==8)%Inside the body of a user-defined function, NARGIN returns the number of input arguments that were used to call the function.
for ind=1:size(Colony1,1)%ind=1:5,对所有食物源进行贪婪选择
if (FitEmp2(ind)>FitEmp(ind))%如果Vi的适应度值大于Xi的,替换,,
oBas(ind)=0;
%zj因为这是已经被新的位置更新了,所以其开采度应该置为零,表示这是第一次,没有被开采过
Fit(ind)=FitEmp2(ind);
Obj(ind)=ObjEmp2(ind);
Colony(ind,:)=Colony2(ind,:);
else%否则不变,并且计数器bas+1
oBas(ind)=fbas(ind)+1;
%zj因为新的位置的适应度没有当前的好(大),所以在当前位置上仍保留当前解,表示当前又被开采了一次
Fit(ind)=FitEmp(ind);
Obj(ind)=ObjEmp(ind);
Colony(ind,:)=Colony1(ind,:);
end;
end; %for
end; %if
if(nargin==9)%第i个引领蜂被跟随,只对第i个食物源进行贪婪选择
ind=i;
if (FitEmp2(ind)>FitEmp(ind))
oBas(ind)=0;
Fit(ind)=FitEmp2(ind);
Obj(ind)=ObjEmp2(ind);
Colony(ind,:)=Colony2(ind,:);
else
oBas(ind)=fbas(ind)+1;
Fit(ind)=FitEmp(ind);
Obj(ind)=ObjEmp(ind);
Colony(ind,:)=Colony1(ind,:);
end;
end;
GlobalMins=zeros(ABCOpts.RunTime,ABCOpts.MaxCycles);
for r=1:ABCOpts.RunTime
% Initialise population
Range = repmat((ABCOpts.ub-ABCOpts.lb),[ABCOpts.ColonySize ABCOpts.Dim]);
Lower = repmat(ABCOpts.lb, [ABCOpts.ColonySize ABCOpts.Dim]);
Colony = rand(ABCOpts.ColonySize,ABCOpts.Dim) .* Range + Lower;%生成初始Colony,其中ColonySize行,Dim列,10*5
%zj先初始化种群规模。。。这个就是算法中式子:x(j)i=x(j)min+rand(0,1)(x(j)max-x(j)min)
Employed=Colony(1:(ABCOpts.ColonySize/2),:);%前一半为引领蜂或食物源,5*5
%zj再将种群的前一半作为引领蜂规模
%evaluate and calculate fitness
ObjEmp=feval(ABCOpts.ObjFun,Employed);%计算引领蜂组Employed的每一行(每一个食物源Xi)的目标函数值,1*5
FitEmp=calculateFitness(ObjEmp);%计算食物源的适应度值,1*5
%set initial values of Bas
Bas=zeros(1,(ABCOpts.ColonySize/2));%1*5,每一列对应每一个Xi没有被更新的次数
GlobalMin=ObjEmp(find(ObjEmp==min(ObjEmp),end));%不带end结果一样,因为ObjEmp为一个列向量,找出目标函数ObjEmp中最小的值给了GlobalMin,1*1
GlobalParams=Employed(find(ObjEmp==min(ObjEmp),end),:);%GlobalParams存放目标函数ObjEmp最小时对应的解,1*5
Cycle=1;
while ((Cycle <= ABCOpts.MaxCycles)),%开始循环
%%%%% Employed phase
Employed2=Employed;%Employed2的每一行对应于Employed每一行的邻域搜索值,即Employed每一行代表Xij,Employed2每一行代表Vij
for i=1:ABCOpts.ColonySize/2%对Xij的每一个i,只有一个j改变。
Param2Change=fix(rand*ABCOpts.Dim)+1;%对应于j
%zj这就是算法中要找的xij中的j,其是Dim中的一个随机数
neighbour=fix(rand*(ABCOpts.ColonySize/2))+1;%对应于k
while(neighbour==i)
neighbour=fix(rand*(ABCOpts.ColonySize/2))+1;
end;
%zj因为k不能取和i相同的值,所以这里如果取到的k正好等于i,那么将重新随机选取一个值
Employed2(i,Param2Change)=Employed(i,Param2Change)+(Employed(i,Param2Change)-Employed(neighbour,Param2Change))*(rand-0.5)*2;
%不能超过上下界
%zj这个就是算法中式子:vij=xij+suijishu(xij-xkj),上式中(rand-0.5)*2就是为了限制suijishu的范
%围控制在(-1,1)之间的
if (Employed2(i,Param2Change)
end;
if (Employed2(i,Param2Change)>ABCOpts.ub)
Employed2(i,Param2Change)=ABCOpts.ub;
end;
%zj可能出于规范的考虑,前面设置了参数lb和ub就是用来限定新的位置不应该越界,如果比下限小,则将下限赋给它,如果比上限大
%则将上线赋给它
end;
ObjEmp2=feval(ABCOpts.ObjFun,Employed2);%计算每一个Vi的目标函数值,5*1
FitEmp2=calculateFitness(ObjEmp2);%计算每一个Vi的适应度值,5*1
[Employed ObjEmp FitEmp Bas]=GreedySelection(Employed,Employed2,ObjEmp,ObjEmp2,FitEmp,FitEmp2,Bas,ABCOpts);
%zj Employed:之前的位置数组; Employed2:更新位置后的数组;
%ObjEmp:之前的目标函数值(每只蜜蜂); ObjEmp2:更新位置后的目标函数值(即每只蜜蜂的函数值)
%Bas:表示被开采的次数; ABCOpts:整个结构体zj
%贪婪原则选择,Employed ObjEmp FitEmp分别对应选择后的食物源,函数值和适应度
%Normalize
NormFit=FitEmp/sum(FitEmp);%50*1,每一行对应于Xi和Vi较优解的Pi
%%% Onlooker phase
Employed2=Colony((ABCOpts.ColonySize/2)+1:ABCOpts.ColonySize,:);
%zj本来这句是Employed2=Employed;但是通过本人阅读论文来看,一般情况是总样本数=引领蜂数量+跟随蜂数量;引领蜂数量=跟随蜂数量;并
%且,引领蜂是前50%,跟随蜂是后50%zj
i=1;
t=0;
while(t
if(rand
Param2Change=fix(rand*ABCOpts.Dim)+1;
neighbour=fix(rand*(ABCOpts.ColonySize/2))+1;
while(neighbour==i)
neighbour=fix(rand*(ABCOpts.ColonySize/2))+1;
end;
Employed2(i,:)=Employed(i,:);%引领蜂被选中跟随,Employed2(i)为跟随蜂
%跟随蜂进行邻域搜索
Employed2(i,Param2Change)=Employed(i,Param2Change)+(Employed(i,Param2Change)-Employed(neighbour,Param2Change))*(rand-0.5)*2;
if (Employed2(i,Param2Change)
end;
if (Employed2(i,Param2Change)>ABCOpts.ub)
Employed2(i,Param2Change)=ABCOpts.ub;
end;
ObjEmp2=feval(ABCOpts.ObjFun,Employed2);%计算跟随蜂邻域搜索解的目标函数
FitEmp2=calculateFitness(ObjEmp2);%计算跟随蜂邻域搜索解的适应度
[Employed ObjEmp FitEmp Bas]=GreedySelection(Employed,Employed2,ObjEmp,ObjEmp2,FitEmp,FitEmp2,Bas,ABCOpts,i);
end;
i=i+1;
if (i==(ABCOpts.ColonySize/2)+1) %如果超出范围,将i至1
i=1;
end;
end;
%%%Memorize Best
CycleBestIndex=find(FitEmp==max(FitEmp));
CycleBestIndex=CycleBestIndex(end);%我认为可以不要
CycleBestParams=Employed(CycleBestIndex,:);%原本注释是“求每次循环中适度值最小所对应的食物源(解)”我认为是“求每次循环中适度值最大所对应的食物源(解)”
CycleMin=ObjEmp(CycleBestIndex);%原本这句注释是“求每次循环中适度值最小所对应的函数值”,我认为是“求每次循环中适度值最大所对应的函数值”
if CycleMin
GlobalParams=CycleBestParams;
end
GlobalMins(r,Cycle)=GlobalMin;%记录每次循环所对应的全局最小值,1*2000
%% Scout phase
ind=find(Bas==max(Bas));%找到没有被更新次数最多的那个食物源Xi,并把次数和limit比较
ind=ind(end);
if (Bas(ind)>ABCOpts.Limit)
Bas(ind)=0;
%Employed(ind,:)=(ABCOpts.ub-ABCOpts.lb)*(0.5-rand(1,ABCOpts.Dim))*2+ABCOpt
%s.lb;
Employed(ind,:)=(ABCOpts.ub-ABCOpts.lb)*(0.5-rand(1,ABCOpts.Dim))*2;%+ABCOpts.lb;
% Employed2(i,Param2Change)=Employed(i,Param2Change)+(Employed(i,Par
% am2Change)-Employed(neighbour,Param2Change))*(rand-0.5)*2;
%message=strcat('burada',num2str(ind))
end;
ObjEmp=feval(ABCOpts.ObjFun,Employed);
FitEmp=calculateFitness(ObjEmp);
fprintf('Cycle=%d ObjVal=%g\n',Cycle,GlobalMin);
Cycle=Cycle+1;
end % End of ABC
end; %end of runs
if ABCOpts.RunTime==1
%semilogy(GlobalMins,'b');
else
%semilogy(mean(GlobalMins),'b');%若多次执行,求均值
end
%semilogy(mean(GlobalMins))
% title('Mean of Best function values');
% xlabel('cycles');
% ylabel('error');
fprintf('Mean =%g Std=%g\n',mean(GlobalMins(:,end)),std(GlobalMins(:,end)));%输出GlobalMins的均值和方差