基于交叉算子和非均匀变异算子的飞蛾扑火优化算法-附代码
基于交叉算子和非均匀变异算子的飞蛾扑火优化算法
文章目录
- 基于交叉算子和非均匀变异算子的飞蛾扑火优化算法
-
- 1.飞蛾扑火优化算法
- 2. 改进飞蛾扑火优化算法
-
- 2.1 交叉算子
- 2.2 非均匀变异算子
- 3.实验结果
- 4.参考文献
- 5.Matlab代码
- 6.Python代码
摘要:针对飞蛾扑火优化算法收敛速度慢以及计算后期易收敛到局部最优解的问题,提出了一种基于遗传算法交叉算子和非均匀变异算子的改进方法。该方法在飞蛾围绕火焰飞行的计算过程中,采用交叉算子和变异算子对火焰位置进行扰动以生成新的火焰,当新火焰的适应度值优于原火焰时则替换原火焰,以提高算法的随机性,防止算法过快陷入局部最优解。
1.飞蛾扑火优化算法
基础飞蛾扑火优化算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/107764895
2. 改进飞蛾扑火优化算法
2.1 交叉算子
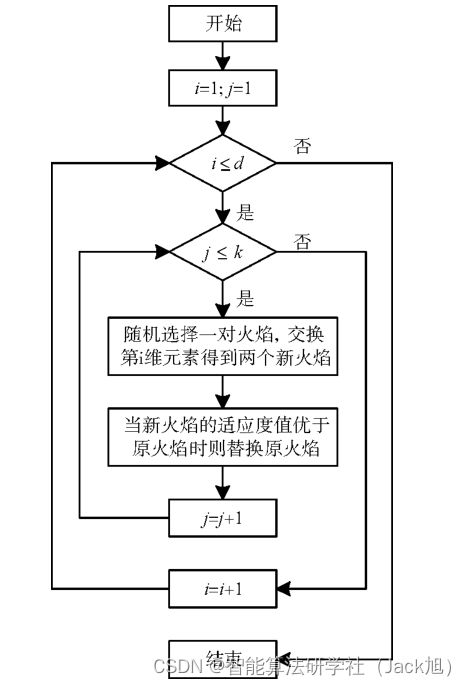
改进方案使用的交叉算子类似于均匀交叉算 子。但不同的是依次针对火焰矩阵的每一维随机 选择 k k k 对火焰进行交叉运算, 每次交叉运算将火焰 对应维度的元素互换并重新计算适应度值, 当新火 焰的适应度值优于原火焰时则替代原火焰, 从而使 其有一定概率跳出局部最优解。交叉运算具体流 程如图 1 所示。其中, d d d 表示火焰位置的维度。 k k k 为常数, 表示进行 k k k 次交叉互换。
2.2 非均匀变异算子
本文选择非均匀变异算子对火焰位置进行扰动,以使火焰在求解初期能在较大范围内搜索并在后期对局部区域进行精细搜索。非均匀算子可表 示如下:
f i , j t + 1 = { f i , j t + Δ ( t , U max j − f i , j t ) , r < 0.5 f i , j t − Δ ( t , f i , j t − U min j ) , r ≥ 0.5 (5) f_{i, j}^{t+1}= \begin{cases}f_{i, j}^{t}+\Delta\left(t, U_{\max }^{j}-f_{i, j}^{t}\right), & r<0.5 \\ f_{i, j}^{t}-\Delta\left(t, f_{i, j}^{t}-U_{\min }^{j}\right), & r \geq 0.5\end{cases} \tag{5} fi,jt+1={fi,jt+Δ(t,Umaxj−fi,jt),fi,jt−Δ(t,fi,jt−Uminj),r<0.5r≥0.5(5)
其中, f i , j f_{i, j} fi,j 表示火焰矩阵中第 i i i 个火焰第 j j j 维的元 素。 t t t 为当前迭代次数。 U max U_{\text {max }} Umax 和 U min U_{\text {min }} Umin 分别表示搜 索空间每一维度的最大值和最小值。 r r r 为区间 [ 0 , 1 ] [0,1] [0,1] 之间的随机数。 Δ ( t , y ) \Delta(t, y) Δ(t,y) 可表示如下:
Δ ( t , y ) = y ⋅ ( 1 − r ( 1 − t T ) b ) (6) \Delta(t, y)=y \cdot\left(1-r^{\left(1-\frac{t}{T}\right)^{b}}\right) \tag{6} Δ(t,y)=y⋅(1−r(1−Tt)b)(6)
其中, T T T 为最大迭代次数, b b b 为决定非均匀度的参 数。在使用非均匀变异算子对火焰位置进行扰动 时, 依次针对每个火焰随机选择 k k k 个维度进行扰 动, 每次扰动产生的新火焰优于原火焰时则替换原 火焰。变异运算流程如图 2 所示。其中, n n n 表示火 焰总数量。 k k k 为常数, 表示进行 k k k 次位置扰动。
3.实验结果
4.参考文献
[1]张保东,张亚楠,郭黎明,江进礼,赵严振.基于交叉算子和非均匀变异算子的飞蛾扑火优化算法[J].计算机与数字工程,2020,48(11):2622-2627.