Python AI：如何构建神经网络并进行预测

人工智能概述

从根本上讲，使用人工智能的目标是让计算机像人类一样思考。这似乎是新事物，但该领域诞生于 1950 年代。

想象一下，您需要编写一个使用 AI解决数独问题的 Python 程序。实现这一点的一种方法是编写条件语句并检查约束以查看是否可以在每个位置放置一个数字。好吧，这个 Python 脚本已经是 AI 的应用程序了，因为您编写了一台计算机来解决问题！

机器学习 (ML)和深度学习 (DL)也是解决问题的方法。这些技术与 Python 脚本之间的区别在于 ML 和 DL 使用训练数据而不是硬编码规则，但它们都可以用于使用 AI 解决问题。在接下来的部分中，您将详细了解这两种技术的区别。

学习资源汇总腾讯文档-在线PDFhttps://docs.qq.com/pdf/DR1doYmNBYUZ3RVNX

机器学习

机器学习是一种训练系统解决问题的技术，而不是对规则进行显式编程。回到上一节中的数独示例，要使用机器学习解决问题，您需要从已解决的数独游戏中收集数据并训练统计模型。统计模型是一种数学形式化的近似现象行为的方法。

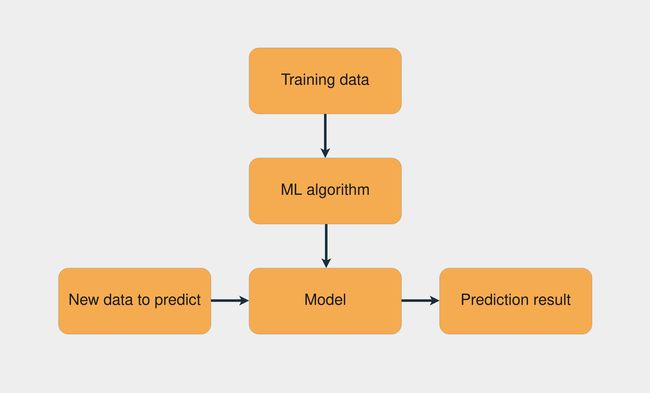
一个常见的机器学习任务是监督学习，其中您有一个包含输入和已知输出的数据集。任务是使用此数据集来训练一个模型，该模型根据输入预测正确的输出。下图展示了使用监督学习训练模型的工作流程：

训练机器学习模型的工作流

训练数据与机器学习算法的结合创建了模型。然后，使用此模型，您可以对新数据进行预测。

注意： scikit-learn是一个流行的 Python 机器学习库，它提供了许多有监督和无监督的学习算法。要了解更多信息，请查看使用 scikit-learn 的 train_test_split() 拆分您的数据集。

监督学习任务的目标是对新的、看不见的数据进行预测。为此，您假设这些看不见的数据遵循与训练数据集分布相似的概率分布。如果将来此分布发生变化，则您需要使用新的训练数据集再次训练模型。

特征工程

当您使用不同类型的数据作为输入时，预测问题变得更加困难。数独问题相对简单，因为您直接处理数字。如果你想训练一个模型来预测句子中的情绪怎么办？或者，如果您有一个图像，并且想知道它是否描绘了一只猫，该怎么办？

输入数据的另一个名称是特征，特征工程是从原始数据中提取特征的过程。在处理不同类型的数据时，您需要找出表示这些数据的方法，以便从中提取有意义的信息。

特征工程技术的一个例子是词形还原，您可以在其中删除句子中单词的屈折变化。例如，动词“watch”的屈折形式，如“watches”、“watching”和“watched”，将被简化为它们的引理或基本形式：“watch”。

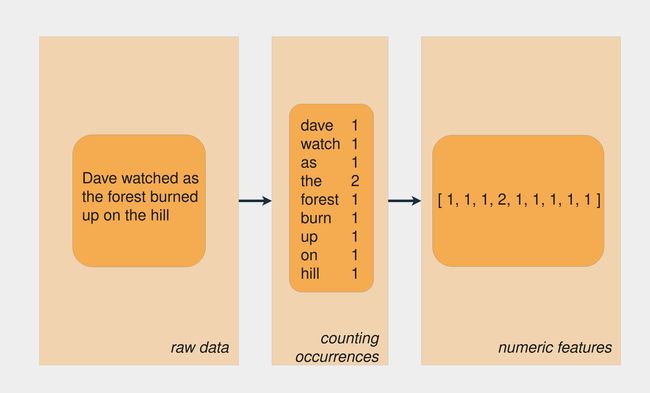
如果您使用数组来存储语料库的每个单词，那么通过应用词形还原，您最终会得到一个不太稀疏的矩阵。这可以提高某些机器学习算法的性能。下图展示了使用词袋模型进行词形还原和表示的过程：

使用词袋模型创建特征

首先，每个词的屈折形式都归结为它的引理。然后，计算该词的出现次数。结果是一个包含文本中每个单词出现次数的数组。

深度学习

深度学习是一种让神经网络自行确定哪些特征重要的技术，而不是应用特征工程技术。这意味着，通过深度学习，您可以绕过特征工程过程。

不必处理特征工程是件好事，因为随着数据集变得越来越复杂，这个过程变得越来越困难。例如，你将如何提取数据来预测一个人的情绪，给她一张脸的照片？使用神经网络，您无需担心，因为网络可以自行学习特征。在接下来的部分中，您将深入研究神经网络，以更好地了解它们的工作原理。

神经网络：主要概念

神经网络是一个通过以下步骤学习如何进行预测的系统：

1. 获取输入数据
2. 做出预测
3. 将预测与所需输出进行比较
4. 调整其内部状态以正确预测下一次

向量、层和线性回归是神经网络的一些构建块。数据存储为向量，使用 Python 可以将这些向量存储在数组中。每一层都会转换来自前一层的数据。您可以将每一层视为特征工程步骤，因为每一层都提取了先前数据的一些表示。

神经网络层的一个很酷的事情是相同的计算可以从任何类型的数据中提取信息。这意味着您使用的是图像数据还是文本数据并不重要。两种情况下，提取有意义信息和训练深度学习模型的过程是相同的。

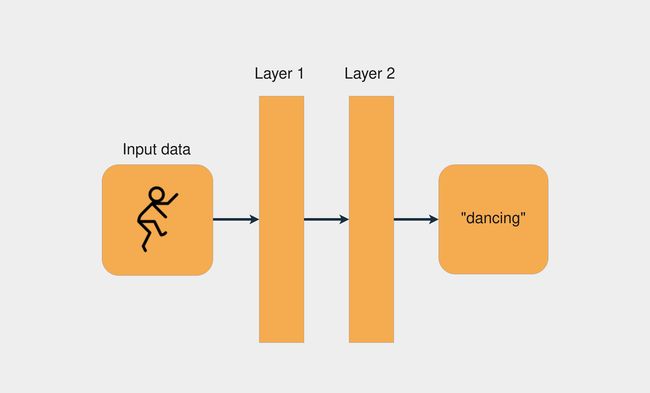
在下图中，您可以看到一个具有两层的网络架构示例：

一个两层的神经网络

每一层都通过应用一些数学运算来转换来自前一层的数据。

训练神经网络的过程

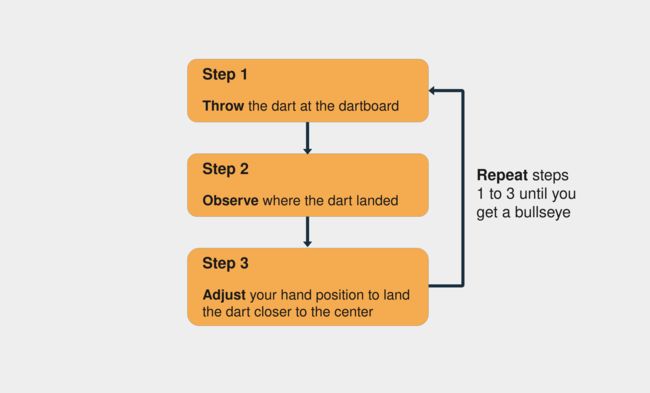
训练神经网络类似于反复试验的过程。想象一下，您是第一次玩飞镖。在您的第一次投掷中，您尝试击中飞镖板的中心点。通常，第一次拍摄只是为了了解手的高度和速度如何影响结果。如果你看到飞镖高于中心点，那么你调整你的手把它扔得低一点，依此类推。

这些是尝试击中飞镖板中心的步骤：

击中飞镖板中心的步骤

请注意，您通过观察飞镖落下的位置来不断评估错误（第 2 步）。你继续前进，直到你最终击中飞镖板的中心。

对于神经网络，该过程非常相似：您从一些随机权重和偏置向量开始，进行预测，将其与所需的输出进行比较，然后调整向量以在下次更准确地预测。该过程一直持续到预测和正确目标之间的差异最小。

知道何时停止训练以及设置什么样的准确率目标是训练神经网络的一个重要方面，主要是因为过拟合和欠拟合的情况。

向量和权重

使用神经网络包括对向量进行操作。您将向量表示为多维数组。向量在深度学习中很有用，主要是因为一种特殊的操作：点积。两个向量的点积告诉您它们在方向上的相似程度，并按两个向量的大小进行缩放。

神经网络中的主要向量是权重和偏置向量。松散地说，您希望神经网络做的是检查输入是否与它已经看到的其他输入相似。如果新输入与之前看到的输入相似，那么输出也将相似。这就是您获得预测结果的方式。

线性回归模型

当您需要估计一个因变量与两个或多个自变量之间的关系时使用回归。线性回归是一种将变量之间的关系近似为线性的方法。该方法可以追溯到十九世纪，是最流行的回归方法。

注意：甲线性关系是其中有一个自变量和因变量之间的直接关系。

通过将变量之间的关系建模为线性关系，您可以将因变量表示为自变量的加权和。因此，每个自变量将乘以一个名为 的向量weight。除了权重和自变量之外，您还添加了另一个向量：偏差。当所有其他自变量都为零时，它会设置结果。

作为如何构建线性回归模型的真实示例，假设您想要训练一个模型来根据面积和房屋的年龄来预测房屋的价格。您决定使用线性回归对这种关系进行建模。以下代码块显示了如何用伪代码为所述问题编写线性回归模型：

price = (weights_area * area) + (weights_age * age) + bias

在上面的例子中，有两个权重：weights_area和weights_age。训练过程包括调整权重和偏差，以便模型可以预测正确的价格值。为此，您需要计算预测误差并相应地更新权重。

这些是神经网络机制如何工作的基础知识。现在是时候看看如何使用 Python 应用这些概念了。

Python AI：开始构建你的第一个神经网络

构建神经网络的第一步是从输入数据生成输出。您将通过创建变量的加权总和来做到这一点。您需要做的第一件事是用 Python 和NumPy表示输入。

用 NumPy 包装神经网络的输入

您将使用 NumPy 将网络的输入向量表示为数组。但是在使用 NumPy 之前，最好先在纯 Python 中使用向量来更好地理解发生了什么。

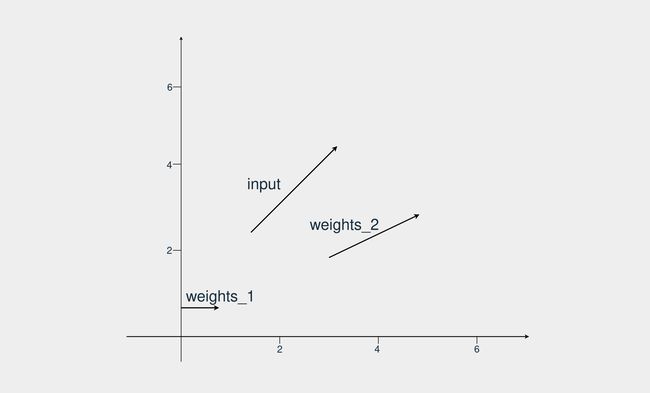
在第一个示例中，您有一个输入向量和其他两个权重向量。目标是找到哪个权重与输入更相似，同时考虑方向和大小。如果您绘制它们，这就是向量的外观：

笛卡尔坐标平面中的三个向量

weights_2更类似于输入向量，因为它指向相同的方向并且幅度也相似。那么如何使用 Python 找出哪些向量相似呢？

首先，您定义三个向量，一个用于输入，另外两个用于权重。然后计算input_vector和weights_1的相似程度。为此，您将应用点积。由于所有向量都是二维向量，因此以下是执行此操作的步骤：

1. 将 的第一个索引乘以 的第input_vector一个索引weights_1。
2. 将 的第二个索引乘以 的第二input_vector个索引weights_2。
3. 将两个乘法的结果相加。

您可以使用 IPython 控制台或Jupyter Notebook进行操作。每次开始一个新的 Python 项目时都创建一个新的虚拟环境是一个很好的做法，所以你应该先这样做。venv附带 Python 3.3 及更高版本，它对于创建虚拟环境非常方便：

$ python -m venv ~/.my-env
$ source ~/.my-env/bin/activate

使用上述命令，您首先创建虚拟环境，然后激活它。现在是使用pip. 由于您还需要 NumPy 和Matplotlib，因此最好也安装它们：

(my-env) $ python -m pip install ipython numpy matplotlib
(my-env) $ ipython

现在您已准备好开始编码。这是计算的点积代码input_vector和weights_1：

>>>

In [1]: input_vector = [1.72, 1.23]
In [2]: weights_1 = [1.26, 0]
In [3]: weights_2 = [2.17, 0.32]

In [4]: # Computing the dot product of input_vector and weights_1
In [5]: first_indexes_mult = input_vector[0] * weights_1[0]
In [6]: second_indexes_mult = input_vector[1] * weights_1[1]
In [7]: dot_product_1 = first_indexes_mult + second_indexes_mult

In [8]: print(f"The dot product is: {dot_product_1}")
Out[8]: The dot product is: 2.1672

点积的结果是2.1672。现在您知道如何计算点积，是时候使用np.dot()NumPy 了。以下是如何dot_product_1使用计算np.dot()：

>>>

In [9]: import numpy as np

In [10]: dot_product_1 = np.dot(input_vector, weights_1)

In [11]: print(f"The dot product is: {dot_product_1}")
Out[11]: The dot product is: 2.1672

np.dot()做你之前做的同样的事情，但现在你只需要指定两个数组作为参数。现在，让我们计算的点积input_vector和weights_2：

>>>

In [10]: dot_product_2 = np.dot(input_vector, weights_2)

In [11]: print(f"The dot product is: {dot_product_2}")
Out[11]: The dot product is: 4.1259

这一次，结果是4.1259。作为对点积的另一种思考方式，您可以将向量坐标之间的相似性视为一个开关。如果乘法结果是0，那么你会说坐标不相似。如果结果不是0，那么您会说它们是相似的。

这样，您可以将点积视为向量之间相似性的松散度量。每次乘法结果为0，最终的点积都会有一个较低的结果。再回到本例的载体，因为的点积input_vector和weights_2是4.1259，和4.1259大于2.1672，则意味着input_vector更类似于weights_2。您将在神经网络中使用相同的机制。

注意：如果需要复制粘贴，请点击每个代码块右上角的提示（>>>）。

在本教程中，您将训练一个模型来做出只有两种可能结果的预测。输出结果可以是0或1。这是一个分类问题，是监督学习问题的一个子集，其中您有一个包含输入和已知目标的数据集。这些是数据集的输入和输出：

学习资源汇总腾讯文档-在线PDFhttps://docs.qq.com/pdf/DR1doYmNBYUZ3RVNX

输入向量	目标
[1.66, 1.56]	1
[2, 1.5]	0

该目标是要预测的变量。在本例中，您正在处理一个由数字组成的数据集。这在实际生产场景中并不常见。通常，当需要深度学习模型时，数据会以文件形式呈现，例如图像或文本。

做出你的第一个预测

由于这是您的第一个神经网络，您将保持简单并构建一个只有两层的网络。到目前为止，您已经看到在神经网络中使用的仅有的两个运算是点积和求和。两者都是线性操作。

如果您添加更多层但继续仅使用线性操作，那么添加更多层将没有效果，因为每一层总是与前一层的输入有一定的相关性。这意味着，对于具有多个层的网络，总会有一个预测相同结果的层数较少的网络。

您想要的是找到一种操作，使中间层有时与输入相关，有时不相关。

您可以通过使用非线性函数来实现此行为。这些非线性函数称为激活函数。激活函数有很多种。所述RELU（整流线性单位），例如，是一个函数，其将所有负数到零。这意味着如果权重为负，网络可以“关闭”它，从而增加非线性。

您正在构建的网络将使用sigmoid 激活函数。您将在最后一层使用它，layer_2. 数据集中仅有的两个可能的输出是0和1，并且 sigmoid 函数将输出限制在0和之间的范围内1。这是表示 sigmoid 函数的公式：

Sigmoid函数公式

该Ë是叫做数学常数欧拉数，并且可以使用np.exp(x)来计算Ë。

概率函数为您提供事件可能结果的发生概率。数据集仅有的两个可能的输出是0和1，而伯努利分布也是具有两种可能结果的分布。如果您的问题遵循伯努利分布，则 sigmoid 函数是一个不错的选择，这就是您在神经网络的最后一层使用它的原因。

由于功能限制输出到一个范围的0给1，你会用它来预测概率。如果输出大于0.5，则您会说预测为1。如果它低于0.5，那么您会说预测为0。这是您正在构建的网络内部的计算流程：

神经网络内部的计算流程

黄色六边形代表函数，蓝色矩形代表中间结果。现在是时候将所有这些知识转化为代码了。您还需要用 NumPy 数组包装向量。这是应用上图中显示的功能的代码：

>>>

In [12]: # Wrapping the vectors in NumPy arrays
In [13]: input_vector = np.array([1.66, 1.56])
In [14]: weights_1 = np.array([1.45, -0.66])
In [15]: bias = np.array([0.0])

In [16]: def sigmoid(x):
   ...:     return 1 / (1 + np.exp(-x))

In [17]: def make_prediction(input_vector, weights, bias):
   ...:      layer_1 = np.dot(input_vector, weights) + bias
   ...:      layer_2 = sigmoid(layer_1)
   ...:      return layer_2

In [18]: prediction = make_prediction(input_vector, weights_1, bias)

In [19]: print(f"The prediction result is: {prediction}")
Out[19]: The prediction result is: [0.7985731]

原始预测结果为0.79，高于0.5，因此输出为1。网络做出了正确的预测。现在用另一个输入向量尝试它np.array([2, 1.5])。此输入的正确结果是0。您只需要更改input_vector变量，因为所有其他参数都保持不变：

>>>

In [20]: # Changing the value of input_vector
In [21]: input_vector = np.array([2, 1.5])

In [22]: prediction = make_prediction(input_vector, weights_1, bias)

In [23]: print(f"The prediction result is: {prediction}")
Out[23]: The prediction result is: [0.87101915]

这一次，网络做出了错误的预测。结果应该小于，0.5因为此输入的目标是0，但原始结果是0.87。它做出了错误的猜测，但这个错误有多严重？下一步是找到一种评估方法。

训练你的第一个神经网络

在训练神经网络的过程中，你首先评估误差，然后相应地调整权重。要调整权重，您将使用梯度下降和反向传播算法。梯度下降用于寻找方向和更新参数的速率。

在对网络进行任何更改之前，您需要计算误差。这就是您将在下一部分中执行的操作。

计算预测误差

要了解误差的大小，您需要选择一种测量方法。用来衡量误差的函数称为代价函数，或损失函数。在本教程中，您将使用均方误差 (MSE)作为成本函数。您分两步计算 MSE：

1. 计算预测和目标之间的差异。
2. 将结果乘以自身。

网络可能会因输出高于或低于正确值的值而出错。由于 MSE 是预测与正确结果之间的平方差，因此使用此指标，您将始终得到正值。

这是计算上次预测误差的完整表达式：

>>>

In [24]: target = 0

In [25]: mse = np.square(prediction - target)

In [26]: print(f"Prediction: {prediction}; Error: {mse}")
Out[26]: Prediction: [0.87101915]; Error: [0.7586743596667225]

在上面的例子中，错误是0.75。将差值乘以自身的一个含义是更大的误差会产生更大的影响，而更小的误差会随着它们的减少而变得越来越小。

了解如何减少错误

目标是更改权重和偏差变量，以便减少错误。要了解这是如何工作的，您将仅更改权重变量并暂时保持偏差不变。你也可以去掉 sigmoid 函数，只使用layer_1. 剩下的就是弄清楚如何修改权重以减少错误。

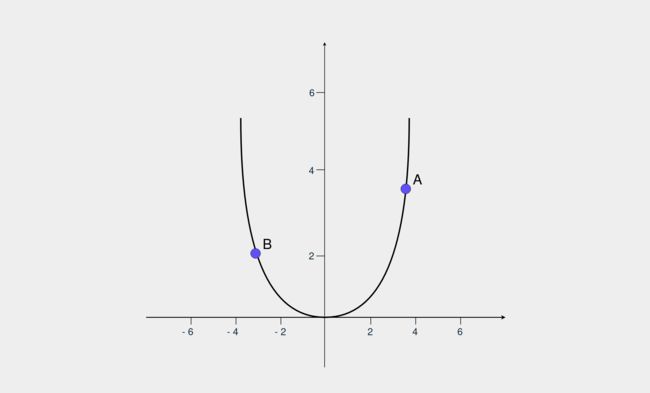
您通过执行 来计算 MSE error = np.square(prediction - target)。如果你把它(prediction - target)当作一个单一的变量x，那么你有error = np.square(x)，它是一个二次函数。如果绘制它，该函数的外观如下所示：

二次函数图

误差由 y 轴给出。如果您有把握A并希望将误差减少到 0，那么您需要x降低该值。另一方面，如果您有把握B并希望减少错误，那么您需要提高x价值。要知道应该朝哪个方向减少误差，您将使用导数。导数准确地解释了模式将如何变化。

导数的另一个词是梯度。梯度下降是用于寻找方向和更新网络参数的速率的算法的名称。

注意：要了解有关梯度下降背后的数学的更多信息，请查看使用 Python 和 NumPy 的随机梯度下降算法。

在本教程中，您不会专注于导数背后的理论，因此您只需将导数规则应用于您将遇到的每个函数。该电源规则规定，导数xⁿ是NX ⁽ ⁿ ⁻¹⁾。所以 的导数np.square(x)是2 * x， 的导数x是1。

请记住，错误表达式是error = np.square(prediction - target). 当您将其(prediction - target)视为单个变量时x，误差的导数为2 * x。通过取这个函数的导数，你想知道你应该向哪个方向改变x以使结果error为零，从而减少误差。

当涉及到您的神经网络时，导数会告诉您更新权重变量应该采取的方向。如果它是一个正数，那么你预测的太高了，你需要降低权重。如果是负数，那么你预测的太低了，你需要增加权重。

现在是时候编写代码来弄清楚如何更新weights_1之前的错误预测。如果均方误差为0.75，那么您应该增加还是减少权重？由于导数是2 * x，您只需要将预测和目标之间的差异乘以2：

>>>

In [27]: derivative = 2 * (prediction - target)

In [28]: print(f"The derivative is {derivative}")
Out[28]: The derivative is: [1.7420383]

结果是1.74，一个正数，所以你需要减少权重。您可以通过减去权重向量的导数结果来实现。现在您可以相应地更新weights_1并再次预测以查看它如何影响预测结果：

>>>

In [29]: # Updating the weights
In [30]: weights_1 = weights_1 - derivative

In [31]: prediction = make_prediction(input_vector, weights_1, bias)

In [32]: error = (prediction - target) ** 2

In [33]: print(f"Prediction: {prediction}; Error: {error}")
Out[33]: Prediction: [0.01496248]; Error: [0.00022388]

误差下降到几乎0！很漂亮吧？在这个例子中，微分结果很小，但有些情况下微分结果太高。以二次函数的图像为例。高增量并不理想，因为您可以从一个点A一直到另一个点B，永远不会接近零。为了解决这个问题，您可以使用衍生结果的一小部分来更新权重。

要定义用于更新权重的分数，请使用alpha参数，也称为学习率。如果你降低学习率，那么增量会更小。如果增加它，则步骤更高。你怎么知道最好的学习率值是多少？通过猜测和试验。

注：传统的默认学习速率值是0.1，0.01和0.001。

如果您采用新的权重并使用第一个输入向量进行预测，那么您将看到现在它对该向量进行了错误的预测。如果您的神经网络对训练集中的每个实例都做出了正确的预测，那么您可能有一个过度拟合的模型，该模型只记住如何对示例进行分类，而不是学习注意数据中的特征。

有一些技术可以避免这种情况，包括对随机梯度下降进行正则化。在本教程中，您将使用在线随机梯度下降。

现在您知道如何计算误差以及如何相应地调整权重，是时候回去继续构建您的神经网络了。

应用链式法则

在您的神经网络中，您需要更新权重和偏置向量。您用来测量误差的函数取决于两个自变量，权重和偏差。由于权重和偏差是自变量，您可以更改和调整它们以获得您想要的结果。

您正在构建的网络有两层，并且由于每一层都有自己的功能，因此您正在处理一个功能组合。这意味着错误函数仍然是np.square(x)，但现在x是另一个函数的结果。

重申这个问题，现在您想知道如何改变weights_1和bias减少错误。您已经看到，您可以为此使用导数，但现在您有了一个使用其他函数生成结果的函数，而不是内部只有和的函数。

由于现在您有了这个函数组合，要获取有关参数的误差的导数，您需要使用微积分中的链式法则。使用链式法则，您可以获取每个函数的偏导数，评估它们，然后将所有偏导数相乘以获得所需的导数。

现在您可以开始更新权重。您想知道如何更改权重以减少错误。这意味着您需要计算误差对权重的导数。由于误差是通过组合不同的函数来计算的，因此您需要取这些函数的偏导数。

下面是如何应用链式法则来找到误差相对于权重的导数的直观表示：

学习资源汇总腾讯文档-在线PDFhttps://docs.qq.com/pdf/DR1doYmNBYUZ3RVNX

显示神经网络内部偏导数的图表

粗体红色箭头显示您想要的导数，derror_dweights。您将从红色六边形开始，采用逆向路径进行预测并计算每个函数的偏导数。

在上图中，每个函数由黄色六边形表示，偏导数由左侧的灰色箭头表示。应用链式法则， 的值derror_dweights将如下：

derror_dweights = (
    derror_dprediction * dprediction_dlayer1 * dlayer1_dweights
)

要计算导数，您可以乘以从误差六边形（红色）到找到权重的六边形（最左边的绿色）的路径的所有偏导数。

你可以说的导数y = f(x)是导数f相对于x。使用此命名法，对于derror_dprediction，您想知道计算相对于预测值的误差的函数的导数。

这个反向路径称为反向传递。在每次向后传递中，您计算​​每个函数的偏导数，用它们的值替换变量，最后将所有值相乘。

这个“取偏导数、求值和乘法”部分是你如何应用链式法则的。这种更新神经网络参数的算法称为反向传播。

使用反向传播调整参数

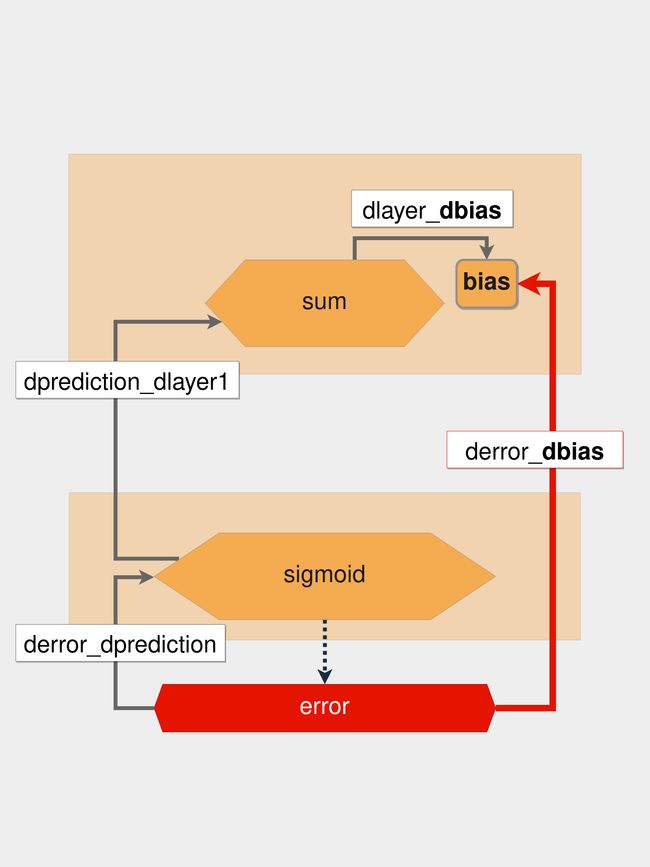
在本节中，您将逐步完成反向传播过程，从如何更新偏差开始。您想取误差函数关于偏差的导数，derror_dbias。然后你将继续向后走，取偏导数，直到找到bias变量。

由于您是从末尾开始向后移动，因此您首先需要针对预测取误差的偏导数。就是derror_dprediction下图中的：

显示用于计算偏置梯度的偏导数的图表

产生误差的函数是一个平方函数，这个函数的导数是2 * x，正如你之前看到的。您应用了一阶偏导数 ( derror_dprediction) 并且仍然没有得到偏差，因此您需要再退一步并获取相对于前一层的预测导数，dprediction_dlayer1。

预测是 sigmoid 函数的结果。您可以通过乘以sigmoid(x)和来获得 sigmoid 函数的导数1 - sigmoid(x)。这个导数公式非常方便，因为您可以使用已经计算出的 sigmoid 结果来计算它的导数。然后你取这个偏导数并继续倒退。

现在您将取layer_1关于偏差的导数。就是这样——你终于做到了！该bias变量是一个自变量，所以应用幂律后的结果是1。很酷，既然你已经完成了这个反向传递，你可以把所有东西放在一起并计算derror_dbias：

>>>

In [36]: def sigmoid_deriv(x):
   ...:     return sigmoid(x) * (1-sigmoid(x))

In [37]: derror_dprediction = 2 * (prediction - target)
In [38]: layer_1 = np.dot(input_vector, weights_1) + bias
In [39]: dprediction_dlayer1 = sigmoid_deriv(layer_1)
In [40]: dlayer1_dbias = 1

In [41]: derror_dbias = (
   ...:     derror_dprediction * dprediction_dlayer1 * dlayer1_dbias
   ...: )

要更新权重，您遵循相同的过程，向后取偏导数，直到到达权重变量。由于您已经计算了一些偏导数，您只需要计算dlayer1_dweights。点积的导数是第一个向量乘以第二个向量的导数，再加上第二个向量乘以第一个向量的导数。

创建神经网络类

现在您知道如何编写表达式来更新权重和偏差。是时候为神经网络创建一个类了。类是面向对象编程 (OOP)的主要构建块。将NeuralNetwork类生成的权重和偏置随机变量的初始值。

实例化NeuralNetwork对象时，需要传递learning_rate参数。您将用于predict()进行预测。您在本节中学到的方法_compute_derivatives()和_update_parameters()计算。这是最后一NeuralNetwork堂课：

class NeuralNetwork:
    def __init__(self, learning_rate):
        self.weights = np.array([np.random.randn(), np.random.randn()])
        self.bias = np.random.randn()
        self.learning_rate = learning_rate

    def _sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    def _sigmoid_deriv(self, x):
        return self._sigmoid(x) * (1 - self._sigmoid(x))

    def predict(self, input_vector):
        layer_1 = np.dot(input_vector, self.weights) + self.bias
        layer_2 = self._sigmoid(layer_1)
        prediction = layer_2
        return prediction

    def _compute_gradients(self, input_vector, target):
        layer_1 = np.dot(input_vector, self.weights) + self.bias
        layer_2 = self._sigmoid(layer_1)
        prediction = layer_2

        derror_dprediction = 2 * (prediction - target)
        dprediction_dlayer1 = self._sigmoid_deriv(layer_1)
        dlayer1_dbias = 1
        dlayer1_dweights = (0 * self.weights) + (1 * input_vector)

        derror_dbias = (
            derror_dprediction * dprediction_dlayer1 * dlayer1_dbias
        )
        derror_dweights = (
            derror_dprediction * dprediction_dlayer1 * dlayer1_dweights
        )

        return derror_dbias, derror_dweights

    def _update_parameters(self, derror_dbias, derror_dweights):
        self.bias = self.bias - (derror_dbias * self.learning_rate)
        self.weights = self.weights - (
            derror_dweights * self.learning_rate
        )

你有它：这是你的第一个神经网络的代码。恭喜！这段代码只是把你目前看到的所有部分放在一起。如果要进行预测，请首先创建 的实例NeuralNetwork()，然后调用.predict()：

>>>

In [42]: learning_rate = 0.1

In [43]: neural_network = NeuralNetwork(learning_rate)

In [44]: neural_network.predict(input_vector)
Out[44]: array([0.79412963])

上面的代码做了一个预测，但现在你需要学习如何训练网络。目标是使网络在训练数据集上泛化。这意味着您希望它适应与训练数据集具有相同概率分布的新的、看不见的数据。这就是您将在下一部分中执行的操作。

用更多数据训练网络

您已经为一个数据实例调整了权重和偏差，但目标是使网络泛化整个数据集。随机梯度下降是一种技术，在该技术中，模型在每次迭代时根据随机选择的训练数据进行预测、计算误差并更新参数。

现在是时候创建类的train()方法了NeuralNetwork。您将每 100 次迭代保存所有数据点的误差，因为您想要绘制一个图表，显示该指标如何随着迭代次数的增加而变化。这是train()你的神经网络的最终方法：

 1class NeuralNetwork:
 2    # ...
 3
 4    def train(self, input_vectors, targets, iterations):
 5        cumulative_errors = []
 6        for current_iteration in range(iterations):
 7            # Pick a data instance at random
 8            random_data_index = np.random.randint(len(input_vectors))
 9
10            input_vector = input_vectors[random_data_index]
11            target = targets[random_data_index]
12
13            # Compute the gradients and update the weights
14            derror_dbias, derror_dweights = self._compute_gradients(
15                input_vector, target
16            )
17
18            self._update_parameters(derror_dbias, derror_dweights)
19
20            # Measure the cumulative error for all the instances
21            if current_iteration % 100 == 0:
22                cumulative_error = 0
23                # Loop through all the instances to measure the error
24                for data_instance_index in range(len(input_vectors)):
25                    data_point = input_vectors[data_instance_index]
26                    target = targets[data_instance_index]
27
28                    prediction = self.predict(data_point)
29                    error = np.square(prediction - target)
30
31                    cumulative_error = cumulative_error + error
32                cumulative_errors.append(cumulative_error)
33
34        return cumulative_errors

上面的代码块中发生了很多事情，所以这里逐行分解：

• 第 8 行从数据集中随机选取一个实例。

• 第 14 到 16 行计算偏导数并返回偏差和权重的导数。他们使用_compute_gradients()您之前定义的 。

• 第 18 行使用_update_parameters()您在前一个代码块中定义的更新偏差和权重。

• 第 21 行检查当前迭代索引是否是 的倍数100。您这样做是为了观察错误在每次100迭代中的变化情况。

• 第 24 行开始遍历所有数据实例的循环。

• 第 28 行计算prediction结果。

• 第 29 行计算error每个实例的 。

• 第 31 行是您使用cumulative_error变量累积误差总和的地方。您这样做是因为您想为所有数据实例绘制一个带有错误的点。然后，在第 32 行，将 附加error到cumulative_errors存储错误的数组。您将使用此数组绘制图形。

简而言之，您从数据集中随机选择一个实例，计算梯度，并更新权重和偏差。您还可以每 100 次迭代计算一次累积误差，并将这些结果保存在一个数组中。您将绘制此数组以可视化训练过程中误差的变化情况。

注意：如果您在 Jupyter Notebook 中运行代码，则需要在添加train()到NeuralNetwork类后重新启动内核。

为了让事情不那么复杂，您将使用一个只有 8 个实例的数据集，即input_vectors数组。现在您可以调用train()并使用 Matplotlib 绘制每次迭代的累积误差：

>>>

In [45]: # Paste the NeuralNetwork class code here
   ...: # (and don't forget to add the train method to the class)

In [46]: import matplotlib.pyplot as plt

In [47]: input_vectors = np.array(
   ...:     [
   ...:         [3, 1.5],
   ...:         [2, 1],
   ...:         [4, 1.5],
   ...:         [3, 4],
   ...:         [3.5, 0.5],
   ...:         [2, 0.5],
   ...:         [5.5, 1],
   ...:         [1, 1],
   ...:     ]
   ...: )

In [48]: targets = np.array([0, 1, 0, 1, 0, 1, 1, 0])

In [49]: learning_rate = 0.1

In [50]: neural_network = NeuralNetwork(learning_rate)

In [51]: training_error = neural_network.train(input_vectors, targets, 10000)

In [52]: plt.plot(training_error)
In [53]: plt.xlabel("Iterations")
In [54]: plt.ylabel("Error for all training instances")
In [54]: plt.savefig("cumulative_error.png")

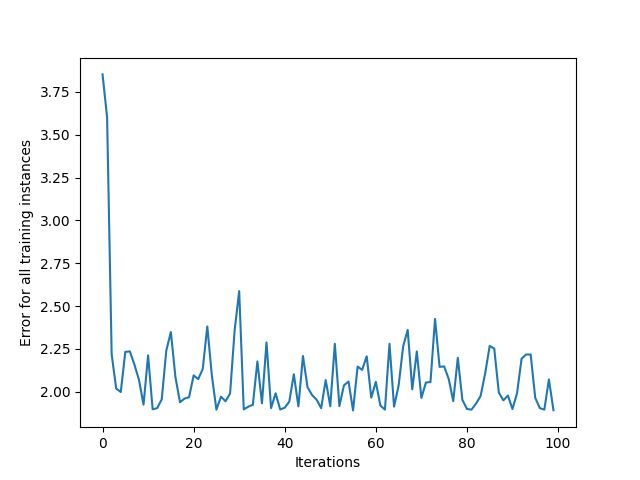
您NeuralNetwork再次实例化该类并train()使用input_vectors和target值进行调用。您指定它应该运行10000时间。这是显示神经网络实例的错误的图表：

学习资源汇总腾讯文档-在线PDFhttps://docs.qq.com/pdf/DR1doYmNBYUZ3RVNX

显示累积训练误差的图表

总体误差正在减少，这正是您想要的。该图像在您运行 IPython 的同一目录中生成。在最大的减少之后，误差从一个交互到另一个交互快速上升和下降。那是因为数据集是随机的，而且非常小，所以神经网络很难提取任何特征。

但使用此指标评估性能并不是一个好主意，因为您正在使用网络已经看到的数据实例对其进行评估。这可能会导致过度拟合，当模型非常适合训练数据集而无法推广到新数据时。

向神经网络添加更多层

出于学习目的，本教程中的数据集很小。通常，深度学习模型需要大量数据，因为数据集更为复杂且有很多细微差别。

由于这些数据集具有更复杂的信息，因此仅使用一两层是不够的。这就是深度学习模型被称为“深度”的原因。它们通常有很多层。

通过添加更多层和使用激活函数，您可以提高网络的表达能力并可以进行非常高级的预测。这些类型的预测的一个例子是人脸识别，例如当你用手机拍下你的脸时，如果手机识别出你的图像，它就会解锁。

结论

恭喜！今天，您使用 NumPy 从头构建了一个神经网络。有了这些知识，您就可以更深入地探索 Python 中的人工智能世界了。

在本教程中，您学习了：

• 什么是深度学习以及它与机器学习的区别
• 如何用 NumPy表示向量
• 什么是激活函数以及为什么在神经网络中使用它们
• 什么是反向传播算法以及它是如何工作的
• 如何训练神经网络并进行预测

训练神经网络的过程主要包括对向量应用运算。今天，您从头开始仅使用 NumPy 作为依赖项。在生产环境中不建议这样做，因为整个过程可能没有生产力且容易出错。这就是为什么像深刻的学习框架的原因之一Keras，PyTorch和TensorFlow是如此受欢迎。