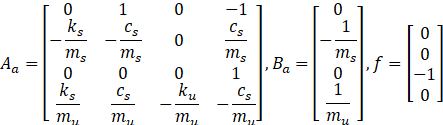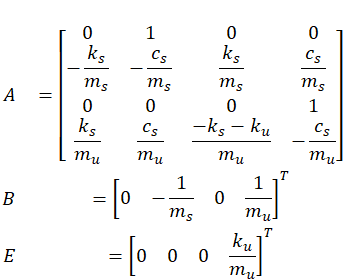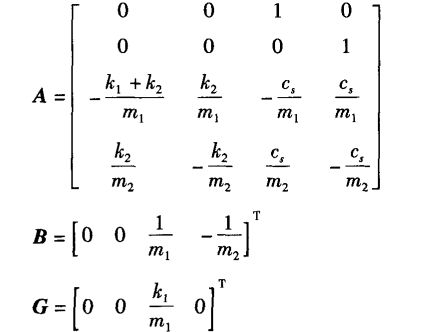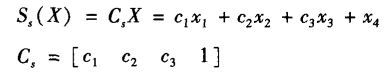几种滑模面选取对2、4、7自由度、整车悬架仿真分析
前言
上几篇文章介绍了各自由度的动力学建模,以及介绍仿真分析了一篇以天棚悬架为参考的滑模跟踪变结构控制,随着滑模文章的阅读,发现滑模面的选取和跟踪结构控制有那么几种常见的几种固定形式,并且与选取的状态变量有关,所以想在这里写一篇关于跟踪变结构控制的综述性文章,并且结合一下自己的滑模面设计和状态变量选取设计控制律,最后进行仿真分析。所以也是作为自己的学习记录,有兴趣的读者欢迎交流学习。这里推荐阅读一下前几篇文章:
线性二自由度模型建立及simulink仿真分析_Mr. 邹的博客-CSDN博客
半车(前后、左右)、整车悬架详细推导建模和simulink仿真分析_Mr. 邹的博客-CSDN博客
基于参考模型的主动悬架滑模控制(详细滑模控制推导)_Mr. 邹的博客-CSDN博客
极点配置法确定滑模面系数_Mr. 邹的博客-CSDN博客
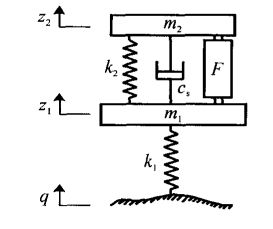
1 2自由度悬架——状态变量形式①+滑模面形式①
1.1选取状态变量
![]()
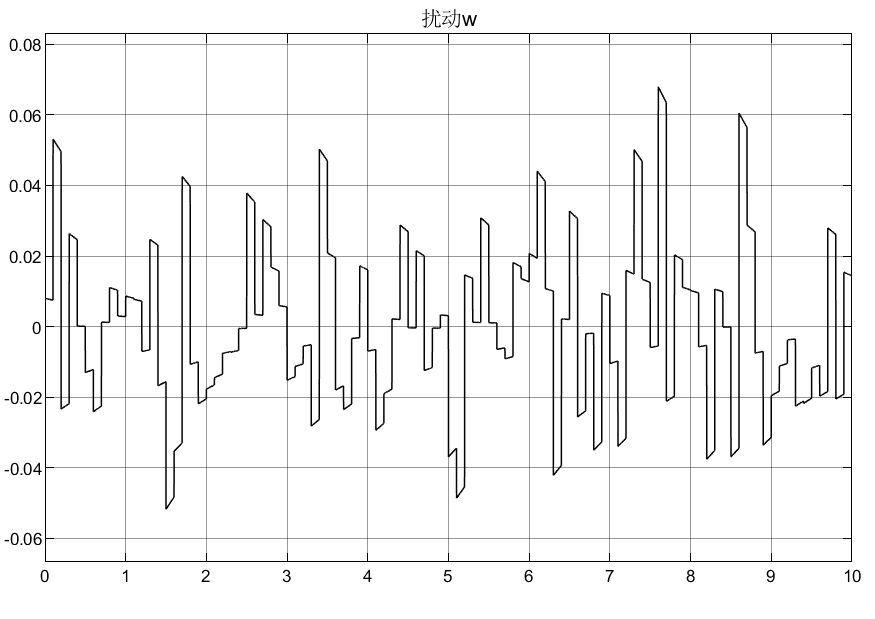
这里以随机路面进行作为路面激励/扰动,由于选取状态变量中含xr,所以w = xr'
1.2 控制器设计
还是以等效滑模的思想进行求取控制律
首先选取切换面:
![]()
忽略扰动项,将状态空间方程代入:
![]()
选用指数趋近律,并进行联立:
![]()
得到控制律为:
![]()
等效控制可以理解为使系统状态沿期望滑模面运动的控制量,切换控制可以理解为驱动系统
状态到达滑模面的控制量。
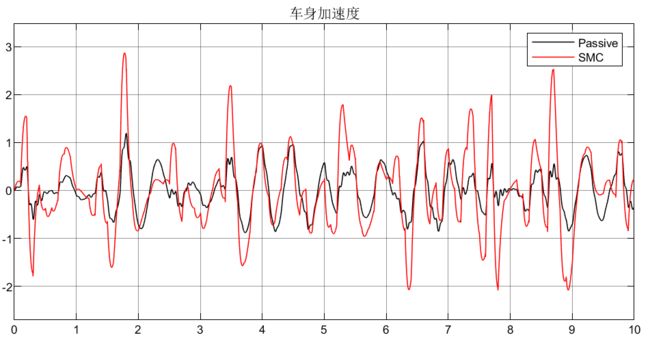
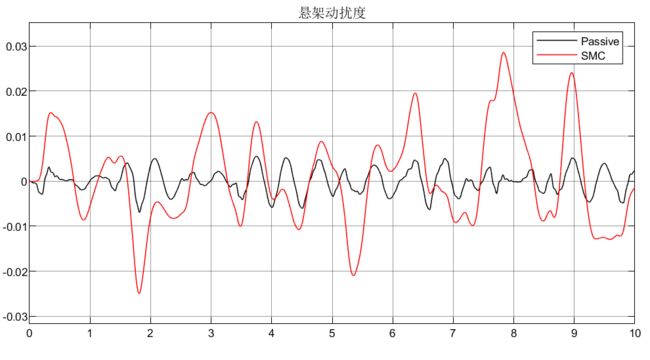
1.3 仿真分析
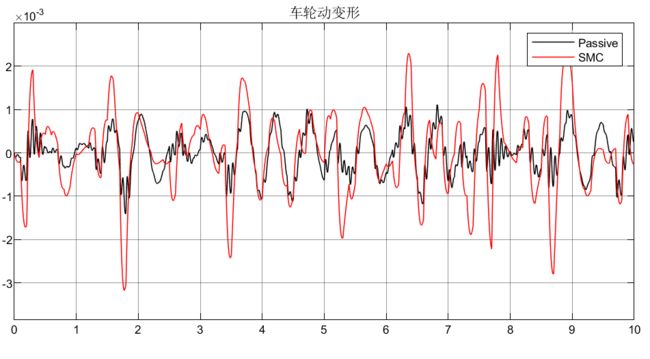
调节参数选取ε = 1,k = 10,为了消抖选取饱和函数代替符号函数;对于滑模面系数的选取采用极点配置法取G = [-1.1535 -0.2409 27.3669 1]。
模型参数:ms = 391;mu = 50.7;ks = 60000;kt = 362000;cs = 1385.4。
(详情见基于参考模型的主动悬架滑模控制(详细滑模控制推导)_Mr. 邹的博客-CSDN博客)
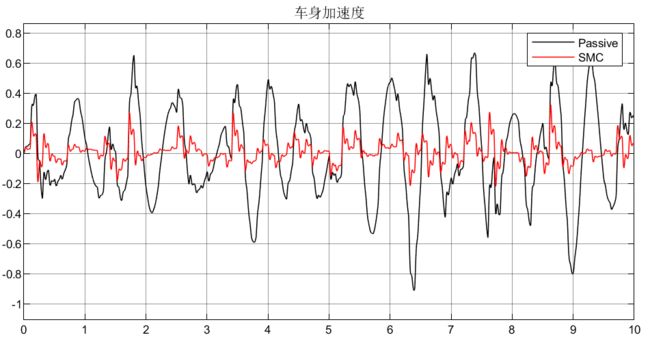
可以看到这样设计选取状态变量以及选取的线性滑模面,性能对于比被动悬架还差(不是仿真有问题,是这样选取状态变量和切换面设计的控制器有问题)
2 2自由度悬架——状态变量形式②+滑模面形式①
2.1选取状态变量
![]()
![]()
2.2 控制器设计
这里和上述选取滑模面一样试试,等于这里只换状态变量,所以控制器仍为:
![]()
2.3 仿真分析
这里用二阶系统的动态性能选择极点,进行极点配置法选取滑模面系数会出现问题,所以参考了下面这篇文献进行复现,它本质上也是通过极点配置法,但是通过Hurwitz判据得到了滑模面系数的选择范围,这里文献和我选取的顺序不一样而已,其实都是可以的。这里先直接拿文献的来复现一下吧。
参考文献:
王健,蔡宇萌. 主动悬架的滑模控制指数趋近率参数优化[J]. 重庆理工大学学报(自然科学版),2017,31(9):15-21. DOI:10.3969/j.issn.1674-8425(z).2017.09.003.
①通过可逆变换将原状态空间方程变为标准型
②对滑模动态方程进行稳定性分析,用Hurwitz判据得到滑模面系数的取值范围
由于很简单,所以这里直接将文献的图拿过来,如果侵权马上删除,仅为学术交流,谢谢理解!
可以看到效果还是不错的,但是认为的调节难以实现最优调节,所以文章提出了用优化算法进行自动调节参数,这个部分放到最后面再来复现。
3 2自由度悬架——状态变量形式②+滑模面形式②
3.1 滑模面选取
可以看到简单的线性滑模面难以获得好的性能输出,这里选用PID滑模面进行设计,并以车身加速度作为误差变量,即
3.2 控制器设计
同理利用等效滑模思想设计控制律
仍然选取指数趋近律,并且选取饱和函数替代符号函数,所以上式u中表达式变为:
3.3 仿真分析
未完待续........
参考文献:
[1]杨金霞. 车辆半主动悬架模型跟踪变结构控制的研究[D]. 江苏:南京林业大学,2006. DOI:10.7666/d.y913537.
[2]王亮. 汽车主动悬架模型跟踪变结构控制研究[D]. 山东:山东理工大学,2009. DOI:10.7666/d.y1507198.
[3]王健,蔡宇萌. 主动悬架的滑模控制指数趋近率参数优化[J]. 重庆理工大学学报(自然科学版),2017,31(9):15-21. DOI:10.3969/j.issn.1674-8425(z).2017.09.003.