粒子群算法总结(保证受益匪浅)——针对多元函数的不同维度的速度和位置约束

目录

前言

1. 多元函数与维度的关系

2.种群大小与维度的关系

3.适应度函数与目标函数的关系

4.个体极值、群体极值、新粒子适应度值有什么区别？

5.维度不同时，速度和维度不同该如何处理？

6.示例仿一求该5元函数的最大值和最小值

6.1求最大值

6.2求最小值

7 示例仿二求该2元函数的最大值和最小值

8.总结

---

前言

这篇博客是用于记录自己学习粒子群算法时，对于几个易混淆概念的理解，并以一个多元函数进行说明，希望对大家有帮助，谢谢！

1. 多元函数与维度的关系

相信很多人开始学习的时候会难以理解维度在PSO中是个什么东西，有什么作用？

首先解释一下，什么叫粒子群的维度：

由于粒子群算法是由鸟在寻找食物时，一群鸟分开寻找找到食物最多的地方，或者最"好"的地方，然后去定居这样的一个思想。所以一个粒子指的是一只鸟，而鸟会朝多个方向去搜索，搜索的方向就叫维度。

而我们函数的优化问题(求最小或者最大值)，就是让此时的变量取到满足最优目标函数值时的解，所以函数的一个变量就指的是一个维度，变量个数=维数。

所以一个粒子代表一个解。

2.种群大小与维度的关系

好了，上面我们知道了维度和变量的关系。既然我们有了维度和粒子数，一个粒子代表一只鸟，那么假设我是一个2维函数的优化问题，即需要朝两个方向去搜索，那么至少得两只鸟(一个方向一只鸟)，但是可想而知，由于每个方向都会有很多个局部最优解，也就是鸟儿自以为这个位置的食物很多，便不再搜寻，这样又没有这个方向的鸟去通知它，所以引出的局部最优的问题，也就等价我们遗传算法中的“早熟”，所以需要每个方向指派多只鸟去搜寻，这便需要种群。

3.适应度函数与目标函数的关系

对于优化问题，常常归结为求最大值和最小值问题两种，所以对于适应度函数的选取有两种，但是都是从目标函数得到，第一种是不管求最大值和最小值，都将适应度函数取维目标函数，那么此时适应度值=目标函数值；第二种是将适应度函数取为目标函数的相反数或者倒数，但是这样处理后最后还要取反或者倒数。两者处理方法的区别在于，第一种求出来的适应度函数随着粒子搜索，也就是随着种群迭代，适应度是越来越小的，这有些不符合自然发展。但是两种处理都能求得我们所需要的最优解。

4.个体极值、群体极值、新粒子适应度值有什么区别？

其实刚开始学习的时候我自己也很晕，为什么好几个极值和适应度值？

后面发现如果我们将适应度函数定义为目标函数，那么这样极值大小=适应度值，这个就不用区分适应度值和极值大小的区别。

首先有必要理清一下粒子群算法的流程，这里还是以之前博客中的一张图片进行说明：

个体极值通俗来讲就是整个搜索过程中，一个粒子搜索的最好的解，这个如果有Swarmsize个粒子，那么便有Swarmsize个解，这Swarmsize个解的集合就叫个体极值。

所以极值更新有两个，一个是个体极值更新，一个是群体极值更新。

个体极值更新：以一个粒子搜索两次来说明，该粒子第二次搜索的适应度值大小与第一次搜索适应度进行比较，如果第二次更好，那么替换掉第一次的，所以这就产生了该粒子搜索的最好适应度值，如果我们将适应度值取为极值，那么就解释了个体极值更新。

群体极值更新：每一次搜索中，选出所有粒子的最好适应度值，也就是一个适应度值，拿这个适应度值与这次粒子搜索的每个适应度值进行比较，如果这个适应度值较差，那么群体适应度值替换掉，如果我们将适应度值取为极值，那么就解释了群体极值更新。

新粒子适应度值：就是指这次搜索后所有粒子搜索到的结果，也就是所有粒子搜索到的适应度值大小。

5.维度不同时，速度和维度不同该如何处理？

下面我们进入一个稍微难点的问题，那么对于多元问题，如果每个变量的约束不同，也就是每个维度的粒子搜索范围和速度不同时，该如何初始化，如何迭代更新？

假如有这样一个5元函数：

 其中x的取值范围为:Xmax = [10 11 12 13 14]，Xmin = [1 2 3 4 5]。同理假设速度也不同，那么该如何初始化呢？首先显然可以看出维度dim = 5

这里有有种办法，一种是用循环，一种是直接定义：

法①用循环：

for i = 1:Swarmsize
    
    V(i,:) = rand(1,dim).*(Vmax-Vmin)+Vmin;%初始化速度
    
    X(i,:) = rand(1,dim).*(Xmax-Xmin)+Xmin;%初始化位置
    
end

法②直接定义：

Vrange = ones(Swarmsize,1)*(Vmax-Vmin);%初始化速度

V(i,:) = rand(Swarmsize,dim)*Vrange+ones(Swarmsize,1)*Vmin;

Xrange = ones(Swarmsize,1)*(Xmax-Xmin);%初始化位置

X(i,:) = rand(Swarmsize,dim)*Xrange+ones(Swarmsize,1)*Xmin;

注：也有的资料会将粒子的初始速度定义为0

6.示例仿一求该5元函数的最大值和最小值

目标函数：

function y = obj2(x)
%x    输入粒子的位置
%y    输出粒子适应度值
y = -5*sin(x(1))*sin(x(2))*sin(x(3))*sin(x(4))*sin(x(5))-...
sin(5*x(1))*sin(5*x(2))*sin(5*x(3))*sin(5*x(4))*sin(5*x(5))+8;

6.1求最大值

clear all
clc
%%  参数设置
c1  = 2;
c2 = 2;
dim = 5;
Xmax = [10 10 10 10 10];
Xmin = [pi/2 pi/2 pi/2 pi/2 pi/2];
Vmax = [0.5 0.5 0.5 0.5 0.5];
Vmin = [-0.5 -0.5 -0.5 -0.5 -0.5];
Swarmsize = 20;
Maxiter = 300;
ws = 0.9;
we = 0.4;

%% 初始化粒子群的速度和位置
%在循环外面初始化
% Vrange = ones(Swarmsize,1)*(Vmax-Vmin);%初始化速度
% V(i,:) = rand(Swarmsize,dim)*Vrange+ones(Swarmsize,1)*Vmin;
% Xrange = ones(Swarmsize,1)*(Xmax-Xmin);%初始化位置
% X(i,:) = rand(Swarmsize,dim)*Xrange+ones(Swarmsize,1)*Xmin;
for i = 1:Swarmsize
    V(i,:) = rand(1,dim).*(Vmax-Vmin)+Vmin;%注意：使用点乘对应项元素相乘
    X(i,:) = rand(1,dim).*(Xmax-Xmin)+Xmin;
    fitness(i) = obj2(X(i,:));%计算初始时刻种群的适应度值，这里直接适应度函数=目标函数
end
%% 寻找初始时刻的个体极值和群体极值(注：极值包括速度和位置两个)
[bestfitness,bestindex] = max(fitness);
Px = X;%个体极值位置，由于是初始时刻，所以所有粒子最好的位置就是初始位置
Pf = fitness;%由于极值定义为适应函数，所以直接用适应度最好代表极值
Gx = X(bestindex,:);%群体极值位置
Gf = bestfitness;%%群体极值大小，所以初始时刻的群体极值即为初始时刻最小的适应度

%% 速度更新和位置更新
for k = 1:Maxiter
    %惯性权重更新
        %             w = 1;%常数惯性权重因子
            w = ws*(ws-we)*(Maxiter-k)/Maxiter;%线性递减惯性权重
%             w = ws-(ws-we)*(k/Maxiter);%非线性递减惯性权重①
%             w = ws-(ws-we)*(k/Maxiter)^2;%非线性递减惯性权重②
%             w = ws+(ws-we)*(2*k/Maxiter-(k/Maxiter)^2);%非线性递减惯性权重③
%             w = we*(ws/we)^(1/(1+10*k/Maxiter));%非线性递减惯性权重④
    for i = 1:Swarmsize
        %速度更新
       V(i,:) = w*V(i,:)+c1*rand*(Px(i,:)-X(i,:))+c2*rand*(Gx-X(i,:));
       %越界处理
       for j = 1:dim
           if V(i,dim) > Vmax(j)
               V(i,dim) = Vmax(j);
           end
           if V(i,dim) < Vmin(j)
               V(i,dim) = Vmin(j);
           end
       end
       %位置更新
       X(i,:) = X(i,:)+V(i,:);
       %越界处理
       for j = 1:dim
           if X(i,dim) > Xmax(j)
               X(i,dim) = Xmax(j);
           end
           if X(i,dim) < Xmin(j)
               X(i,dim) = Xmin(j);
           end
       end
       
       %粒子适应度值计算
       fitness(i) = obj2(X(i,:));
    end
    
       %% 个体极值和群体极值更新(注：极值包括速度和位置两个)
       for i = 1:Swarmsize
           %个体极值更新
           if Pf(i) < fitness(i)%Pf即为上一代粒子的值(因为适应度函数即为目标函数)，
%如果上一代每个粒子适应度值逐个与新种群(当代)每个粒子适应度值对应比较(即同一粒子当代与上一代适应度值进行比较)，如果小于则更新
               Pf(i) = fitness(i);
               Px(i,:) = X(i,:);
           end
           %群体极值更新
           if Gf < fitness(i)%如果当前的群体极值(当前最优解) < 新种群中的某个值，则替换
               Gf = fitness(i);
               Gx = X(i,:);
           end
       end
       result(k) = Gf;
end
disp(['x1=',num2str(Gx(1)),',x2=',num2str(Gx(2)),',x3=',num2str(Gx(3)),',x4=',...
    num2str(Gx(4)),',x5=',num2str(Gx(5)),'时,','最优解为：',num2str(Gf)])
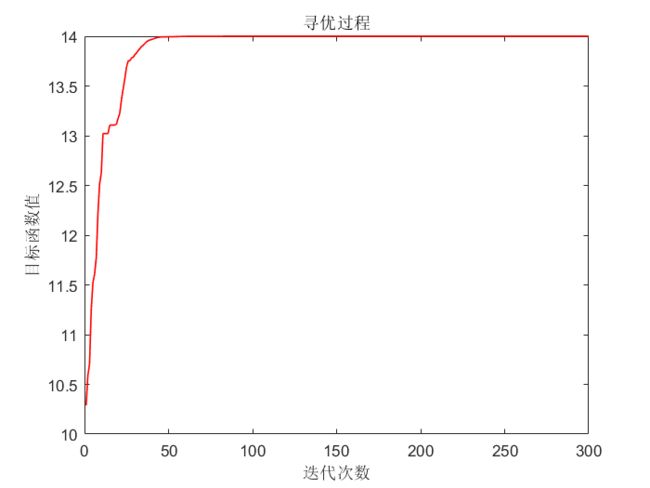
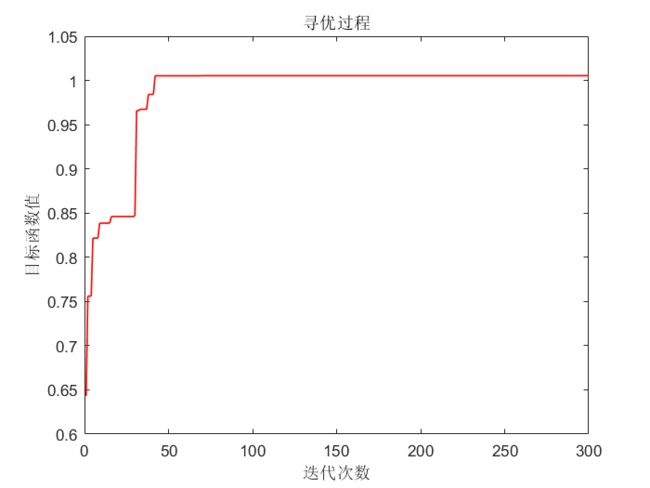
figure(1)
plot(result,'r','linewidth',1)
title("寻优过程");xlabel("迭代次数");ylabel("目标函数值")

寻优结果：

 注：并非每次都能找到最优解，所以后面有必要去学习混合优化算法。

6.2求最小值

如果将适应度函数直接定义为目标函数，稍微做如下几行程序改动即可：

[bestfitness,bestindex] = min(fitness);

if Pf(i) > fitness(i)%Pf即为上一代粒子的值(因为适应度函数即为目标函数)，
if Gf > fitness(i)%如果当前的群体极值(当前最优解) < 新种群中的某个值，则替换

7 示例仿二求该2元函数的最大值和最小值

目标函数：

function y = obj(x)
%x    输入粒子的位置
%y    输出粒子适应度值
y=(sin( sqrt(x(1).^2+x(2).^2) )./sqrt(x(1).^2+x(2).^2)+exp((cos(2*pi*x(1))+cos(2*pi*x(2)))/2)-2.71289);

主程序：

clear all
clc

figure(1)
[x,y]=meshgrid(-2:0.01:2);
z=sin( sqrt(x.^2+y.^2) )./sqrt(x.^2+y.^2)+exp((cos(2*pi*x)+cos(2*pi*y))/2)-2.71289;
mesh(x,y,z)
hold on
%% 迭代参数设置
c1 = 2;c2 = 2;%加速度因子
dim = 2;%搜索维度/变量个数
Maxiter = 300;
Swarmsize = 20;%粒子数量/种群大小
Xmax = [2 2];Xmin = [-2 -2];%搜索的dim维度的位置范围
Vmax = [0.5 0.5];Vmin = [-0.5 -0.5];%搜索的dim维度的速度范围
ws = 0.9;%初始惯性权重
we = 0.4;%迭代至最大次数时的惯性权重
%%  (1)初始化粒子群，粒子适应度值计算
%%可以在循环外面初始化粒子的位置和速度
% range = ones(Swarmsize,1)*(Xmax-Xmin);%Swarmzize个粒子的范围
% X = rand(Swarmsize,dim).*range+ones(Swarmsize,dim)*Xmin;
% %随机产生0-1的100个粒子的3个维度位置，即100*3；再归一化到粒子实际限定的范围
%
% range = ones(Swarmsize,1)*(Vmax-Vmin);%Swarmzize个粒子的范围
% V = rand(Swarmsize,dim).*range+ones(Swarmsize,dim)*Vmin;
for i = 1:Swarmsize
    X(i,:) = rand(1,dim).*(Xmax-Xmin)+Xmin;%在循环里面初始化粒子的位置和速度
    V(i,:) = rand(1,dim).*(Vmax-Vmin)+Vmin;
    
    %粒子适应度计算
    fitness(i) = obj(X(i,:));%将粒子位置代入到目标函数，这里将目标函数直接定义为适应度函数
end

%%   (2)寻找个体极值和群体极值(极值包括速度和适应度值)
[bestfitness,bestfindex] = max(fitness);
Px = X;%个体最佳：所有粒子本身经历过的最优位置(Swarmsize个粒子)。如:第i个粒子在迭代中的数据为x(i,:)
Gx = X(bestfindex,:);%群体最佳:整个粒子群所经历过的最优位置(1个粒子)
Pf = fitness;%个体极值：所有粒子经历过的最优位置的适应度值(Swarmsize个粒子)
% Gf = bestfitness;%群体极值：整个粒子群所经历过的最优位置的适应度值(1个粒子)
Gf = fitness(bestfindex);

h = scatter3(X(:,1),X(:,2),fitness',80,'*r');  % scatter3是绘制3维散点图的函数

for k = 1:Maxiter
    %%  (3)速度更新和位置更新
    
    %惯性权重更新
        %             w = 1;%常数惯性权重因子
%             w = ws*(ws-we)*(Maxiter-k)/Maxiter;%线性递减惯性权重
            w = ws-(ws-we)*(k/Maxiter);%非线性递减惯性权重①
%             w = ws-(ws-we)*(k/Maxiter)^2;%非线性递减惯性权重②
%             w = ws+(ws-we)*(2*k/Maxiter-(k/Maxiter)^2);%非线性递减惯性权重③
%             w = we*(ws/we)^(1/(1+10*k/Maxiter));%非线性递减惯性权重④
    for i = 1:Swarmsize
        %速度更新
        V(i,:) = w*V(i,:)+c1*rand*(Px(i,:)-X(i,:))+c2*rand*(Gx-X(i,:));
        for j = 1:dim        %速度越界处理
            if V(i,j) > Vmax(j)
                V(i,j) = Vmax(j);
            end
            if V(i,j) < Vmin(j)
                V(i,j) = Vmin(j);
            end
        end
        
        %位置更新
        X(i,:) = X(i,:)+V(i,:);
        for j = 1:dim        %位置越界处理
            if X(i,j) > Xmax(j)
                X(i,j) = Xmax(j);
            end
            if X(i,j) < Xmin(j)
                X(i,j) = Xmin(j);
            end
        end
    end
    

    for i = 1:Swarmsize
    %% (4)粒子适应度值计算
        fitness(i) = obj(X(i,:));
    %% (5)个体极值和群体极值更新
        %个体极值更新(极值包括速度和适应度值)
        if Pf(i) < fitness(i)%Pf即为上一代粒子的值(因为适应度函数即为目标函数)，
         %如果上一代每个粒子适应度值逐个与新种群(当代)每个粒子适应度值比较，如果小于则更新
            Pf(i) = fitness(i);
            Px(i,:) = X(i,:);
        end
        
        %群体极值和和位置更新
        if Gf < fitness(i)  %如果当前的群体极值(当前最优解) < 新种群中的某个值，则替换
            Gf = fitness(i);
            Gx = X(i,:);
        end
    end
    result(k) = Gf;%记录群体极值，即寻优轨迹/过程
    pause(0.1)  % 暂停0.1s
    h.XData = X(:,1);  % 更新散点图句柄的x轴的数据
    h.YData = X(:,2);  % 更新散点图句柄的y轴的数据
    h.ZData = fitness';% 更新散点图句柄的z轴的数据
end
%% 结果处理
disp(['x1=',num2str(Gx(1)),',x2=',num2str(Gx(2)),'时,','最优解为：',num2str(Gf)])
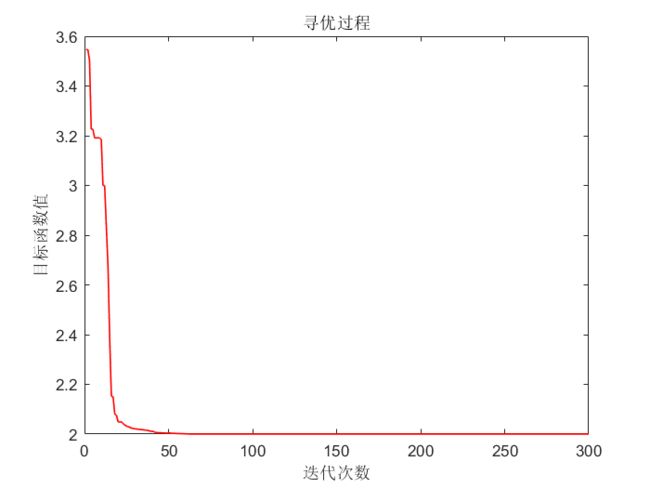
figure(2)
plot(result,'r','linewidth',1)
title("寻优过程");xlabel("迭代次数");ylabel("目标函数值")

结果：

动画展示：

QQ录屏20221019211150

最小值求解大家可以尝试修改一下试试哦，也推荐自己拿代码多练习几个粒子。

8.总结

对于目前的粒子群算法，即使采用动态惯性权重，个人觉得陷入局部最优是其最大的问题，所以很有必要进行改进，或者学习混合优化算法。