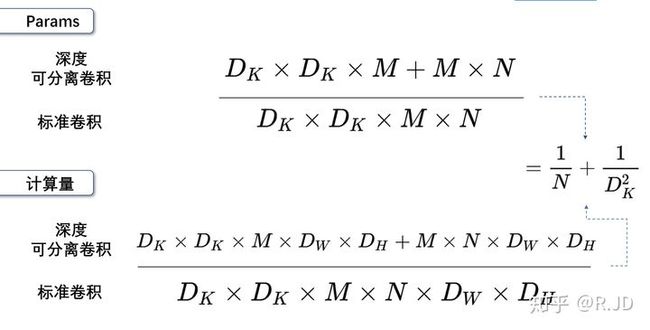MobileNet_v1详解
一、背景介绍
自2012年AlexNet问世以来,CNN被设计得越来越深,越来越复杂,对硬件的要求也就随之提高,而且这些大型网络都是以准确率为导向设计的,很少考虑到效率的优化。但是在实际生活的一些应用中(比如自动驾驶、增强现实等),不仅硬件受限制,而且注重效率,所以越来越多的人开始研究小巧而高效的网络。
当时(2017年)的研究方向可以分为两种,一是压缩复杂网络的预训练模型,二是直接设计并训练小型模型。MobileNet的作者们属于后者,MobileNet不仅可以优化效率(low latency),而且可以让使用者根据硬件限制自行选择适合的模型大小(parameters size)。
二、思路提出
2.1 深度可分离卷积(Depthwise Separable Convolution)
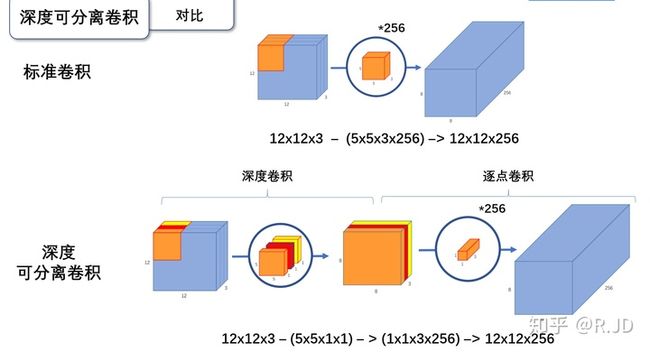
标准卷积层本质上完成了两件事情,一是通过卷积核提取特征(filter),二是将特征图组合起来(combine)。我的理解是,每个卷积核都可以提取特征得到特征图,这完成了第一件事情;将每个卷积核得到的特征图组合起来得到最终输出,这完成了第二件事情。而整个MobileNet的核心理念深度可分离卷积,它通过分解标准卷积,把原先放在一步内完成的filter和combine分成了两个步骤,分别对应两种卷积depthwise convolution和pointwise convolution。
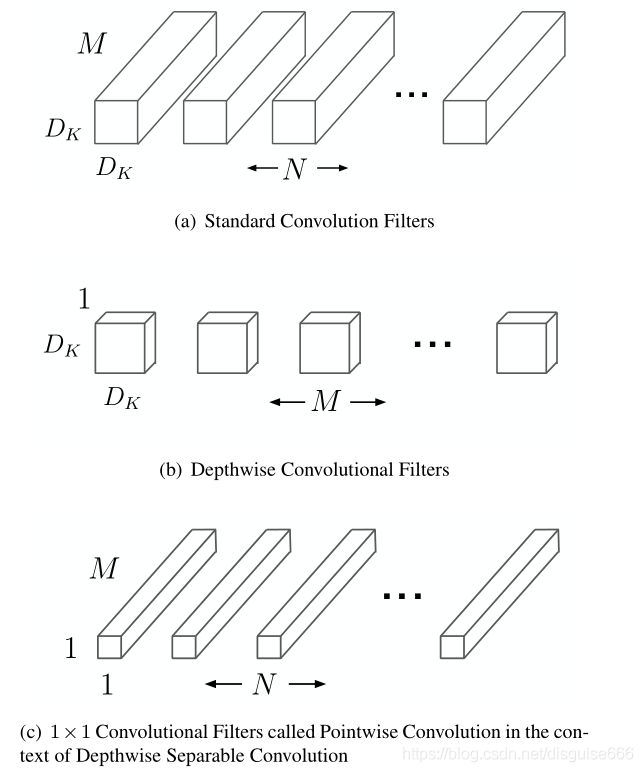
depthwise convolution和标准卷积的区别在于:标准卷积是将每个卷积核应用在所有通道上,而depthwise convolution针对输入中的每个通道应用不同的卷积核。假设输入有 M M M个通道,从上图可以看到,标准卷积层有 N N N个卷积核,每个卷积核尺寸为 D k ∗ D k D_k * D_k Dk∗Dk,通道数为 M M M;depthwise convolution有 M M M个卷积核,每个卷积核的通道数都是1。
但是depthwise convolution的输入和输出维度都是一样的,那怎么改变维度呢?这时候就轮到pointwise convolution出场,其本质为 1 ∗ 1 1 * 1 1∗1的标准卷积,主要作用就是对输入进行升维和降维。下图更加形象地表现了深度可分离卷积的工作过程:
那么这么做的意义是什么?答:减小模型计算量和减少参数量。如果对模型计算量和参数量计算方式不明确,可以先移步CNN卷积层、全连接层的参数量、计算量和神经网络中参数量以及计算量的计算。
假设标准卷积核的尺寸为 D k ∗ D k D_k * D_k Dk∗Dk,通道数为 M M M,数量有 N N N个。标准卷积的参数量为 D k ∗ D k ∗ M ∗ N D_k * D_k * M * N Dk∗Dk∗M∗N,而深度可分离卷积的depthwise convolution参数量为 D k ∗ D k ∗ M D_k * D_k * M Dk∗Dk∗M,pointwise convolution参数量为 1 ∗ 1 ∗ M ∗ N 1 * 1 * M * N 1∗1∗M∗N,两者之和为 D k ∗ D k ∗ M + M ∗ N D_k * D_k * M + M * N Dk∗Dk∗M+M∗N。
现在来计算模型计算量,假设最终得到的输出为 D F ∗ D F ∗ M D_F * D_F * M DF∗DF∗M, N N N个标准卷积核都为 D k ∗ D k ∗ M D_k * D_k * M Dk∗Dk∗M。特征图的每一个点都是一个卷积核进行卷积得来的(只计算乘法操作),那么计算量为 D k ∗ D k ∗ M ∗ N ∗ D F ∗ D F D_k * D_k * M * N * D_F * D_F Dk∗Dk∗M∗N∗DF∗DF。而深度可分离卷积的depthwise convolution计算量为 D k ∗ D k ∗ M ∗ D F ∗ D F D_k * D_k * M * D_F * D_F Dk∗Dk∗M∗DF∗DF,pointwise convolution计算量为 1 ∗ 1 ∗ M ∗ N ∗ D F ∗ D F 1 * 1 * M * N * D_F * D_F 1∗1∗M∗N∗DF∗DF,两者之和为 D k ∗ D k ∗ M ∗ D F ∗ D F + M ∗ N ∗ D F ∗ D F D_k * D_k * M * D_F * D_F + M * N * D_F * D_F Dk∗Dk∗M∗DF∗DF+M∗N∗DF∗DF。
将标准卷积和深度可分离卷积进行比较可得下图:
如果我们用 3 ∗ 3 3 * 3 3∗3的卷积核,因为 N N N相对 D k 2 D_k^2 Dk2来说比较大,所以深度可分离卷积计算量和参数量大致都为原来的 1 9 \frac{1}{9} 91。标准卷积和深度可分离卷积的网络结构对比如下图所示:
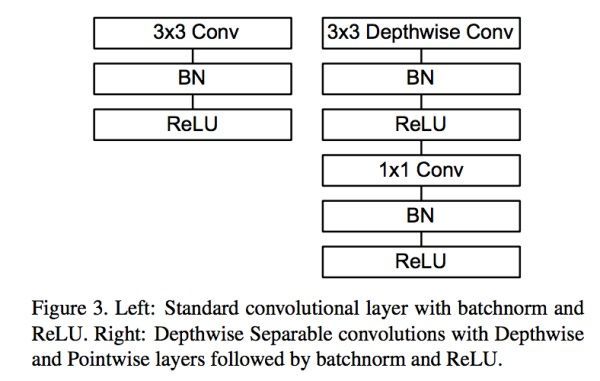
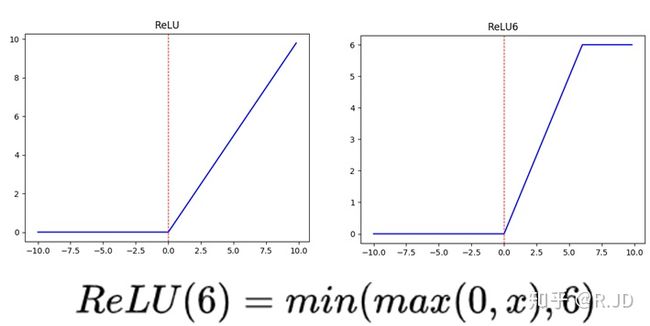
左侧是带有BN和ReLU的 3 ∗ 3 3 * 3 3∗3标准卷积,右侧是深度可分离卷积,但是注意右侧第一个 R e L U ReLU ReLU不是我们平常所见的,而是 R e L U 6 ReLU6 ReLU6,用公式表述为 min ( max ( 0 , x ) , 6 ) \min(\max(0, x), 6) min(max(0,x),6),图像如下:
为什么要用ReLU的原因,引用轻量级神经网络“巡礼”(二)—— MobileNet,从V1到V3:
作者认为ReLU6作为非线性激活函数,在低精度计算下具有更强的鲁棒性。这里所说的“低精度”,可能不是指的float16,而是指的定点运算(
fixed-point arithmetic)。
PyTorch官方实现的MobileNet_v2代码中也可以发现这一细节:
class ConvBNReLU(nn.Sequential):
def __init__(self, in_planes, out_planes, kernel_size=3, stride=1, groups=1):
padding = (kernel_size - 1) // 2
super(ConvBNReLU, self).__init__(
nn.Conv2d(in_planes, out_planes, kernel_size, stride, padding, groups=groups, bias=False),
nn.BatchNorm2d(out_planes),
nn.ReLU6(inplace=True)
)
同样,这份代码里也可以看出depthwise convolution是通过groups参数来实现的。
2.2 Width Multiplier 和 Redolution Multiplier
首先来看看MobileNet的整体结构,如上图所示。这个结构其实还是基于VGG的,只是将标准卷积改成了深度可分离卷积而已。但这是标准的MobileNet,有时候基于实际需求,我们可能还得将其进一步简化以得到更少的参数和计算量,对此作者们引入了两个参数:Width Mulitplier和Resolution Multiplier。
Width Mulitplier的作用是按比例 α \alpha α缩小标准MobileNet每一层的通道数。假设原来输入通道数为 M M M,输出通道数为 N N N,那么缩放后得到的新输入通道数为 α M \alpha M αM,新输出通道数为 α N \alpha N αN。此时深度可分离卷积网络的计算量为:
D k ∗ D k ∗ α M ∗ D F ∗ D F + α M ∗ α N ∗ D F ∗ D F D_k * D_k * \alpha M * D_F * D_F + \alpha M * \alpha N * D_F * D_F Dk∗Dk∗αM∗DF∗DF+αM∗αN∗DF∗DF
其中 a ∈ ( 0 , 1 ] a \in (0, 1] a∈(0,1],一般设置为[1, 0.75, 0.5, 0.25]。Width Mulitplier大致可以将计算量和参数量简化为标准MobileNet的 1 α 2 \frac{1}{\alpha^2} α21。
Revolution Multiplier的作用是按比例 β \beta β缩小特征图的尺寸,比如原来输出特征图大小为 D F ∗ D F D_F * D_F DF∗DF,那么加入 β \beta β的特征图参数大小为 β D F ∗ β D F \beta D_F * \beta D_F βDF∗βDF。同时加入 α , β \alpha, \beta α,β后,深度可分离卷积网络的计算量为:
D k ∗ D k ∗ α M ∗ β D F ∗ β D F + α M ∗ α N ∗ β D F ∗ β D F D_k * D_k * \alpha M * \beta D_F * \beta D_F + \alpha M * \alpha N * \beta D_F * \beta D_F Dk∗Dk∗αM∗βDF∗βDF+αM∗αN∗βDF∗βDF
其中 β ∈ ( 0 , 1 ] \beta \in (0, 1] β∈(0,1],但是resolution multiplier仅仅将计算量大致变为原来的 1 β 2 \frac{1}{\beta^2} β21,不改变参数量。
三、实验结果
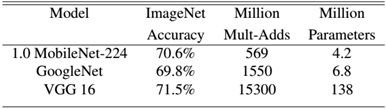
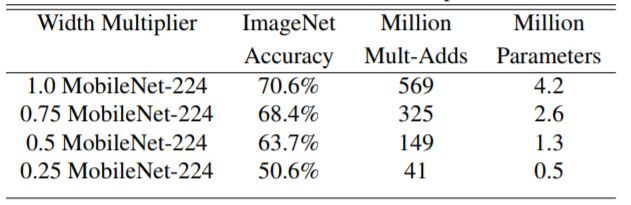
MobileNet是在效率和准确率之间做了一个折中:
如上图所示,标准的MobileNet准确率比VGG16下降了百分之一左右,但是参数量和Multi-adds都大大减少。如果进一步压缩网络,那肯定是会降低准确率的:
四、参考资料
4.1 整体解读
- 轻量级神经网络“巡礼”(二)—— MobileNet,从V1到V3
- 轻量化网络ShuffleNet MobileNet v1/v2 解析
- CNN模型之MobileNet
4.2 Group Convolution
- 轻量化网络ShuffleNet MobileNet v1/v2 解析的开头部分
- PyTorch官方文档-conv2d
- Pytorch Conv2d中groups的作用
- Pytorch - Conv2d 卷积