机器学习笔记(十四)概率图模型
14.概率图模型
14.1隐马尔可夫模型
1、概率模型
机器学习是根据一些已观察到的证据(如训练样本)来对感兴趣的未知变量(如类别标记)进行估计和预测。概率模型(probabilistic model)提供了一种描述框架,将学习任务归结于计算变量的概率分布
在概率模型中,利用已知变量推测未知变量的分布称为推断(inference),其核心是如何基于可观测变量推断出未知变量的条件分布。假定未知变量集合是Y,可观察变量集合是O,其他变量集合是R,生成式(generative)模型考虑联合分布P(Y,R,O);判别式(discriminative)模型考虑条件分布P(Y,R|O);给定一组观测变脸值,推断就是由P(Y,R,O)或P(Y,R|O)得到条件概率分布P(Y|O)。
直接利用概率求和规则消去变量R不可行,因为即便每个变量只有简单的两种取值,复杂度已去到至少O(2|Y|+|R|);并且属性变量之间还可能存在复杂的联系;因此概率模型的学习,即基于训练样本来估计变量分布的参数是困难的。为此需要能表达变量间关系的工具,用于推断和学习算法,概率图模型即是。
2、概率图模型
概率图模型(probabilisticgraphical model)是一类用图来表达变量相关关系的概率模型。概率图模型,以图为表示工具,如一个结点表示一个或一组随机变量,结点之间的边表示变量间的概率相关关系,即变量关系图。
根据边的性质不同,概率图模型大致可分为两类:
1)使用有向无环图表示变量间的依赖关系,称为有向图模型或贝叶斯网(Bayesian network);
2)使用无向图表示变量间的相关关系,称为无向图模型或马尔可夫网(Markov network);
隐马尔可夫模型属于第一种有向网类型。
3、隐马尔可夫模型
隐马尔可夫模型(Hidden Markov Model,HMM)是结构最简单的动态贝叶斯网(dynamic Bayesian network),是著名的有向图模型,主要用于时序数据建模,在语音识别、自然语言处理等领域有广泛应用。
1)HMM结构信息
HMM的变量可分为两组:第一组是状态变量{y1,y2,…,yn},其中yi∈Y表示第i时刻的系统状态,通常假定状态变量是隐藏的、不可观测的,因此状态变量也叫隐变量(hidden variable);第二组是观测变量{x1,x2,…,xn},其中xi∈X表示第i时刻的观测值。
在HMM中,系统通常在多个状态{ s1,s2,…,sN }之间转换,因此状态变量yi的取值范围Y(状态空间)通常是有N个可能取值的离散空间。观测变量xi可以是离散型也可以使连续型,这里仅考虑离散型观测变量,并假定其取值范围X为{ o1,o2,…,oM}。
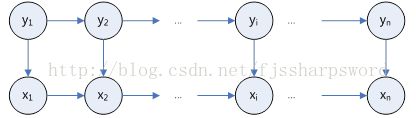
HMM图结构如下:
图中箭头表示了变量间的依赖关系。在任一时刻,观测变量的取值仅依赖于状态变量,即x t由y t确定;与其他状态变量及观测变量的取值无关。t时刻的状态y t仅依赖于t-1时刻的状态y t-1,与其余n-2个状态无关。此为马尔科夫链(Markov chain),即:系统下一时刻的状态仅由当前状态决定,不依赖于以往的任何状态。基于这种依赖关系,所有变量的联合概率分布为:
14.2马尔可夫随机场
马尔可夫随机场(Markov Random Field,MRF)是典型的马尔可夫网,是一种著名的无向图模型。图中每个结点表示一个或一组变量,结点之间的边表示两个变量之间的依赖关系。马尔可夫随机场有一组势函数(potential function),也称因子(factor),这是定义在变量子集上的非负实函数,主要用于定义概率分布函数。
1)MRF定义
马尔可夫随机场是一个无向图模型,图中结点的一个子集,若其中任意两结点间都有边连接,则称该结点子集为一个团(clique)。若在一个团中加入另外任何一个结点都不再形成团,则称该团为极大团(maximalcliuqe),极大团不能被其他团所包含。每个结点至少出现在一个极大团中。如下图:{x2,x5,x6}构成极大团,{x1,x2,x3}不构成团。
在MRF中,多个变量之间的联合概率分布能基于团分解为多个因子的乘积,每个因子仅与一个团相关;就是将原来按结点(变量)的分布分解为按团(变量集合)的分布。具体来说,对于n个变量X={x 1,x 2,…,x n},所有团构成的集合为C,与团Q∈C对应的变量集合记为X Q,则联合概率P(x)定义为:2)全局马尔可夫性
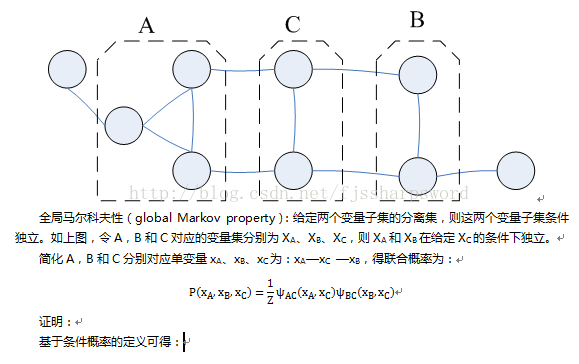
概率模型最重要前提就是条件独立,在MRF中如何得到条件独立性呢?如下图,借助分离概念,若从结点集A中的结点到B中的结点都必须经过结点集C中的结点,则称结点集A和B被结点集C分离,C称为分离集(separating set)。
14.3条件随机场
条件随机场(ConditionalRandom Field,CRF)是一种判别式无向图模型。生成式概率模型是直接对联合分布进行建模;而判别式概率模型则是对条件分布进行建模。HMM和MRF都是生成式模型,CRF则是判别式模型。
条件随机场试图对多个变量在给定观测值后的条件概率进行建模。令x={x1,x2,…,xn}为观测序列,y={y1,y2,…,yn}为与之相应的标记序列,则条件随机场的目标是构建条件概率模型P(y|x)。标记变量y可以是结构型变量,即其分量之间具有某种相关性。如在自然语言处理的词性标注任务中,观测数据为语句(即单词序列),标记为相应的词性序列,具有线性序列结构;在语法分析任务中,输出标记则是语法树,具有树形结构。
令G=(V,E)表示结点与标记变量y中元素一一对应的无向图,y v表示与结点v对应的标记变量,n(v)表示结点v的邻接结点,若图G的每个变量y v都满足马尔可夫性,即:P(y v|x, y V\{v})= P(y v|x, y n(v)),则(y,x)构成一个条件随机场。理论上,图G可具有任意结构,只要能表示标记变量之间的条件独立性关系即可。在现实应用中,对标记序列建模时,最常用的就是链式结构,即链式(chain-structured)条件随机场,如下图。
14.4学习与推断
基于概率图模型定义的联合概率分布,可对目标变量的边际分布(marginal distribution)或以某些可观测变量为条件的条件分布进行推断。边际分布是指对无关变量求和或积分后得到结果。如在马尔可夫网中,变量的联合分布被表示成极大团的势函数乘积,给定参数Θ求解某个变量x的分布,就变成对联合分布中其他无关变量进行积分的过程,称为边际化(marginalization)。
对概率图模型,还要确定具体分布的参数,称为参数估计或参数学习问题,通常使用极大似然估计或最大后验概率估计求解。若将参数视为待推测的变量,则参数估计过程和推断类似,也可以和变量推断问题一致求解。
具体来说,假设图模型所对应的变量集x={x 1,x 2,…,x N}能分为x E和x F两个不相交的变量集,推断问题的目标就是计算边际概率P(x F)或条件概率P(x F|x E)。条件概率:概率图模型的推断方法大致可分为两类。第一个是精确推断方法,希望能计算出目标变量的边际分布,或条件分布的精确值;一般情形下,精确算法的计算复杂度随着极大团规模的增长呈指数增长,适用范围有限;第二个是近似推断方法,希望在较低的时间复杂度下获得原问题的近似解,此类方法在现实任务中更常用。下面两个方法是具有代表性的精确推断方。
1)变量消去
精确推断是一类动态规划算法,利用图模型所描述的条件独立性来削减目标概率值所需的计算量。变量消去法是最直观的精确推断算法,也是构建其他精确推断算法的基础。通过利用乘法对加法的分配律,变量消去法把多个变量的积的求和问题,转化为对部分变量交替进行求积和求和的问题。这种转化使得每次的求和与求积运算限制在局部,仅与部分变量有关,从而简化了计算。不过变量消去法的缺点是:若需计算多个边际分布,重复使用变量消去法会造成大量的冗余计算。
2)信念传播
信念传播(BeliefPropagation)算法将变量消去法的求和操作看作一个消息传递过程,很好地解决了求解多个边际分布时的重复计算问题。
变量消去法通过求和操作:
14.5近似推断
精确推断方法通常需要很大的计算开销,因此在现实应用中近似推断方法更为常用。近似推断方法大致可分为两大类:一类是采样(sampling),通过使用随机化方法完成近似;另一类是使用确定性近似完成近似推断,代表方法是变分推断(variational inference)。2)变分推断
变分推断通过使用已知简单分布来逼近需推断的复杂分布,并通过限制近似分布的类型,从而得到一种局部最优、但具有确定解的近似后验分布。
概率图模型的简洁表示方法-盘式记法(plate notation):N个变量{x 1,x 2,…,x N}均依赖于变量z,将相互独立的、由相同机制生成的多个变量放在一个方框(盘)内,并在方框中标出类似变量重复出现的个数N;方框可以嵌套;用阴影标注出已知的、能观察到的变量。
14.6话题模型
话题模型(topicmodel)是一族生成式有向图模型,主要用于处理离散型的数据(如文本集合),在信息检索、自然语言处理等领域有广泛应用。隐狄利克雷分配模型(Latent Dirichlet Allocation,LDA)是话题模型的典型代表。
关于话题模型的三层概念:
1)词(word):待处理数据的基本离散单元,如文本处理中,一个词就是一个英文单词或有独立意义的中文词;如图像数据中的图像小块就是一个词;
2)文档(document):待处理的数据对象,由一组词组成,这些词在文档中是不计顺序的,如一篇论文、一个网页都可看作一个文档;也称为词袋(bag-of-words);数据对象只要能用词袋描述,就可使用话题模型;
3)话题(topic):表示一个概念,具体表示为一系列相关的词,以及它们在该概念下出现的概率。
形象来说,一个话题就像是一个箱子,里面装着这个概念下出现概率较高的那些词。本章从概率图模型引出HMM,以及生成式MRF和判别式CFR,进而围绕三个基本问题给出精确推断(变量消去和信念传播)和近似推断(MCMC采样和变分推断)解决方法,最后给出话题模型的应用场景。对于HMM的应用场景还是由很多可以着手。