Python算法入门day9——二叉树

1. 二叉树的性质

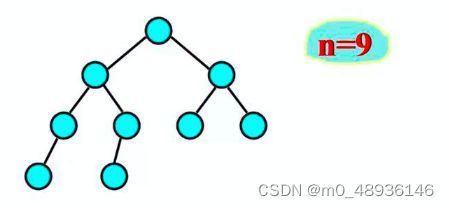
1.具有n个节点的非空二叉树共有n-1个分支。

证明：除了根节点以外，每个节点有且仅有一个双亲节点，即每个结点与其双亲节点之间仅有一个分支存在，因此，具有n个节点的非空二叉树的分支总数为n-1。

2. 非空二叉树的第i层最多有2^(i-1)个结点(i>=1)

3. 深度为h的非空二叉树最多有2^h-1个结点。

(深度为h且具有2^h-1个结点的二叉树为满二叉树。)

4. 若非空二叉树有n0个叶结点，有n2个度为2的结点，则 n0=n2+1

        例：具有1102个结点的完全二叉树一定有__叶子节点。A:79 B:551 C:550 D:552

答案：B

完全二叉树一定存在1度结点，只需要除2向上取整即可，如果是奇数个结点，则存在0个一度结点，如果是偶数个结点，则存在1个一度结点。

5. 具有n个结点的非空完全二叉树的深度为h=(log2^n)+1

 

2. 二叉树的定义

二叉树的链式存储：将二叉树的节点定义为一个对象，节点之间通过类似链表的链接方式来连接。

#二叉树
class BiTreeNode:
    def __init__(self,data):
        self.data=data #存储节点中的数据
        self.lchild=None #左孩子
        self.rchild=None #右孩子
#案例
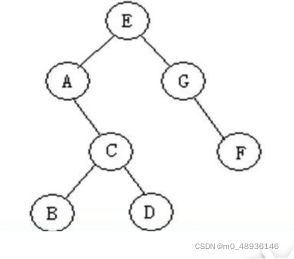
a=BiTreeNode("A")
b=BiTreeNode("B")
c=BiTreeNode("C")
d=BiTreeNode("D")
e=BiTreeNode("E")
f=BiTreeNode("F")
g=BiTreeNode("G")
e.rchild=g
e.lchild=a
a.rchild=c
c.lchild=b
c.rchild=d
g.rchild=f

root=e
#想找c
print(root.lchild.rchild.data)#C

---

3. 二叉树的遍历

二叉树的遍历方式一共有四种常用的，即前序遍历，中序遍历，后序遍历以及层次遍历。

1.前序遍历 ：EACBDGF

【代码实现】

class BiTreeNode:
    def __init__(self,data):
        self.data=data #存储节点中的数据
        self.lchild=None #左孩子
        self.rchild=None #右孩子
#案例
a=BiTreeNode("A")
b=BiTreeNode("B")
c=BiTreeNode("C")
d=BiTreeNode("D")
e=BiTreeNode("E")
f=BiTreeNode("F")
g=BiTreeNode("G")
e.rchild=g
e.lchild=a
a.rchild=c
c.lchild=b
c.rchild=d
g.rchild=f
root=e #根

def pre_order(root):
    if root: #当root不为空时
        print(root.data,end=" ") #先输出
        pre_order(root.lchild) #再递归左孩子
        pre_order(root.rchild) #最后递归右孩子
pre_order(root) #E A C B D G F

---

2.中序遍历：A B C D E G F

def in_order(root):
    if root:
        in_order(root.lchild)
        print(root.data,end=" ")
        in_order(root.rchild)
in_order(root) #A B C D E G F

---

3.后序遍历：B D C A F G E

def end_order(root):
    if root:
        end_order(root.lchild) #先遍历左孩子
        end_order(root.rchild) #再遍历右孩子
        print(root.data,end=" ") #最后输出
end_order(root) #B D C A F G E

---

4.层次遍历：E A G C F B D

一层一层的从左往右遍历(广义优先，BFS)

        1.定义队列，存放E

        2.E出队，A，G进队

        3.A出队，C进队

        4.G出队，F进队

        5.C出队，B，D进队

        6.然后依次出队就得到了E A G C F B D

from collections import deque
#层次遍历BFS
def level_order(root):
    queue=deque()
    queue.append(root)
    while len(queue)>0:#只要队列不空
        node=queue.popleft()#删除第一个元素
        print(node.data,end=' ')
        #判断左右节点是否存在，如果存在，存放到队列中
        if node.lchild:#表示左孩子存在
            queue.append(node.lchild)
        if node.rchild:#表示右孩子存在
            queue.append(node.rchild)
level_order(root)#E A G C F B D

---

4. 二叉搜索树

1.二叉搜索树的定义

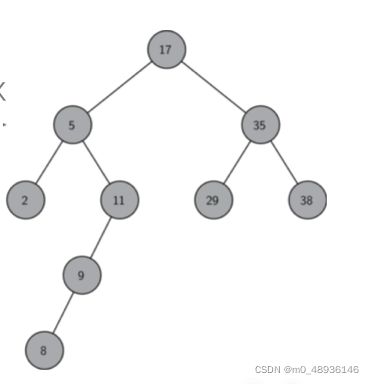
        二叉搜索树是一颗二叉树且满足性质：设x是二叉树的一个节点。如果y是x的左子树的一个节点，那么y.key<=x.key;如果y是x的右子数的一个节点，那么y.key>=x.key

这个定义什么意思呢？

比如17这个节点 ，左边的子节点比自身小，右边的字节点比自身大

再比如5这个点，左边的2比5小，右边的11比5大

大概就是这么个意思

2.二叉搜索树的操作：插入,搜索

创建一个BST类，比节点小的放左边遍历，大的放右边遍历

class BiTreeNode:
    def __init__(self,data):
        self.data=data
        self.lchild=None #左孩子
        self.rchild=None #右孩子
        self.parent=None #父节点

class BST:
    def __init__(self,li=None):
        self.root=None
        if li:
            for val in li:
                self.insert_no_rec(val)
    #方法一：递归
    def insert(self,Node,val):#节点，插入的值
        if not Node: #如果node为空
            Node=BiTreeNode(val)
        #如果不为空，分三种情况，大于小于等于
        elif valNode.data:
            Node.rchild=self.insert(Node.lchild,val)
            Node.rchild.parent=Node
        #等于先不与考虑
        return Node
    
    #方法二：非递归
    def insert_no_rec(self,val):
        p=self.root #先定义一个p表示根节点，再进来的数与p做比较，左小右大
        #首先判断p是否为none
        if not p:
            #如果p是空的话，直接给根节点赋值
            self.root=BiTreeNode(val)
            return
        while True:
            if valp.data:
                if p.rchild:
                    p=p.rchild
                else:
                    p.rchild=BiTreeNode(val)
                    p.rchild.parent=p
                    return
            else: #等于的时候什么都不敢
                return
    def pre_order(self,root):
        if root:
            print(root.data,end=' ')
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)
    def in_order(self,root):
        if root:
            self.in_order(root.lchild)
            print(root.data,end=" ")
            self.in_order(root.rchild)
    def end_order(self,root):
        if root:
            self.end_order(root.lchild)
            self.end_order(root.rchild)
            print(root.data,end=" ")

    #查询 方法一：递归 
    #递归是需要node值的，非递归不需要
    def query(self,node,val):
        if not node:#如果没有节点
            return None
        if node.dataval:#从左找
            return self.query(node.lchild,val)
        else: #等于
            return node

    #查询 方法二：非递归
    def query_no_rec(self,val):
        p=self.root
        while p:
            if p.dataval:
                p=p.lchild
            else: #如果等于
                return p
        return p
        
#案例
tree=BST([2,3,6,1,9,8,4,5,7])

tree.pre_order(tree.root)
print(" ")
tree.in_order(tree.root)
print(" ")
tree.end_order(tree.root)
print(" ")

#查找
print(tree.query_no_rec(1).data)#1 

---

【运行结果】

2 1 3 6 4 5 9 8 7  
1 2 3 4 5 6 7 8 9  
1 5 4 7 8 9 6 3 2 

1