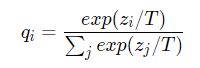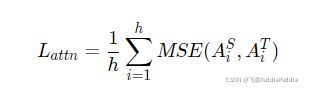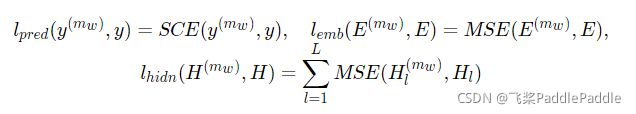预训练模型蒸馏 -- 宽度自适应策略蒸馏TinyBERT
预训练模型蒸馏
在前面的课程中,大家了解了自然语言处理领域中一些经典的模型,比如BERT、ERNIE等,它们在NLP任务中的强大之处是毫无疑问的,但由于预训练模型的参数较多,体积庞大,在部署时对设备的运算速度和内存大小以及能耗都有着极高的要求。但当我们处理实际的产业应用需求时,比如将深度学习模型部署到手机上时,就需要对模型进行压缩,在不影响性能的前提下使其变得体积更小、速度更快、能耗更低。本节课我们会先对预训练模型蒸馏中几个比较经典的模型进行介绍,比如:Patient-KD、DistilBERT、TinyBERT和DynaBERT。从原理和结构上对以上几个模型进行详解。然后再通过一个实验案例,带领大家使用DynaBERT训练策略中宽度自适应部分来对TinyBERT在GLUE基准数据集的QQP任务中进行蒸馏,以此进行实际效果验证。
资源
-
更多CV和NLP中的transformer模型(BERT、ERNIE、ViT、DeiT、Swin Transformer等)、深度学习资料,请参考:awesome-DeepLearning
-
了解并使用更多模型压缩相关工具,请参考:PaddleSlim
模型压缩简介
模型压缩方法主要可以分为以下四类:
-
参数修剪和量化(Parameter pruning and quantization):用于消除对模型表现影响不大的冗余参数。早期工作表明,网络修剪和量化在降低网络复杂性和解决过拟合问题上是有效的。它可以为神经网络带来正则化效果从而提高泛化能力。参数修剪和量化可以进一步分为三类:量化和二值化,网络剪枝和结构化矩阵。量化可以看作是“量子级别的减肥”,神经网络模型的参数一般都用float32的数据表示,但如果我们将float32的数据计算精度变成int8的计算精度,则可以牺牲一点模型精度来换取更快的计算速度。而剪枝则类似“化学结构式的减肥”,将模型结构中对预测结果不重要的网络结构剪裁掉,使网络结构变得更加 ”瘦身“。比如,在每层网络,有些神经元节点的权重非常小,对模型加载信息的影响微乎其微。如果将这些权重较小的神经元删除,则既能保证模型精度不受大影响,又能减小模型大小。结构化矩阵则是用少于 $m \times n$ 个参数来描述一个 $m \times n$ 阶矩阵,以此来减少内存消耗。
-
低秩分解(Low-rank factorization):卷积神经网络中的主要计算量在于卷积计算,而卷积计算本质上是矩阵分析问题,因此可以通过对多维矩阵进行分解的方式,用多个低秩矩阵来逼近该矩阵,比如将一个3D卷积转换为3个1D卷积,从而降低参数复杂度和运算复杂度。
-
迁移/压缩卷积滤波器(Transferred/compact convolutional filters):通过构造特殊结构的卷积滤波器来降低存储空间、减小计算复杂度。
-
知识蒸馏(Knowledge distillation):类似“老师教学生”,使用一个效果好的大模型指导一个小模型训练,因为大模型可以提供更多的软分类信息量,所以会训练出一个效果接近大模型的小模型。
在本节课中,我们主要讲述以知识蒸馏的方法对BERT(transformer-based)模型进行压缩。
知识蒸馏
2014年,Geoffrey Hinton在 Distilling the Knowledge in a Neural Network 中提出知识蒸馏(KD)概念:把从一个复杂的大模型(Teacher Network)上学习到的知识迁移到另一个更适合部署的小模型上(Student Network),叫知识蒸馏。
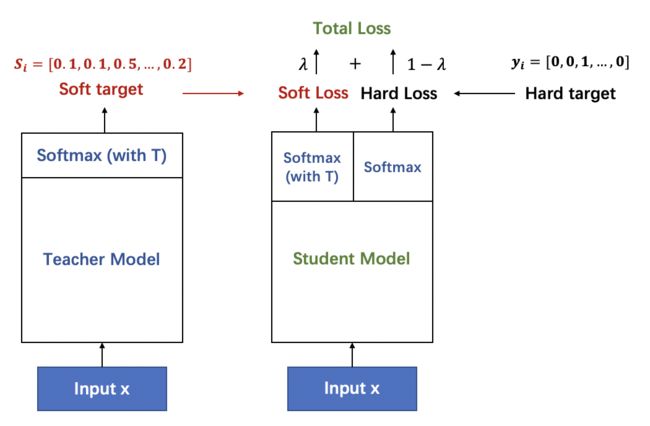
知识蒸馏结构
如上图所示,左边的教师网络是一个复杂的大模型,以它带有温度参数T的softmax输出作为软目标作为学生网络学习的软目标。学生网络在学习时,也通过带有温度参数T的softmax进行概率分布预测,与软目标计算soft loss。同时,也通过正常的训练流程获得预测的样本类别与真实的样本类别计算hard loss。最终根据 $\gamma * soft loss + (1 - \gamma) * hard loss$ 作为损失函数来训练学生网络。
其中,知识蒸馏过程中涉及到的两种标签分别是:
-
硬标签(hard target):网络训练的目标,即分类任务中正确分类的label,正标签为1,其余标签都为0;
-
软标签(soft target):大模型的softmax层输出的类别概率,正标签的概率最高。
论文中提出的softmax函数中增加了温度(Temperature)这个参数,其公式如下:
其中,T代表温度。原始的softmax函数就是 $T=1$ 的情况。那么,为什么要增加一个变量T呢?一个复杂高性能网络往往可以获得很好的分类效果,也就是说预测错误的概率会比预测正确的概率小得多。但是一个小的网络,可能很难达到复杂的大网络的性能。T参数的加入就是为了帮助小网络可以更好的学习到大网络对负标签的判断信息。在传统的训练过程中(仅使用hard target),所有负标签都是零,被全部统一对待。但是加入T,T越高,softmax的类概率分布会越平滑,就可以将大模型对每一个标签的学习信息都传递给小模型。
举一个例子,假设一个三分类问题,z_0 = 2.2, z_1 = 0.8, z_2 = 0.2,那么当 T = 1 时,
当 T = 10时,
 可以看到,T越高,softmax的类分布概率会变得越平滑。这就使得学生网络可以学习到教师网络对负标签归纳的信息。
可以看到,T越高,softmax的类分布概率会变得越平滑。这就使得学生网络可以学习到教师网络对负标签归纳的信息。
手写数字识别任务(图来源于参考文献3)
举个例子,如上图所示,在用MNIST数据集做手写数字识别任务时,某个输入的“2”更加类似“3”,则softmax的输出值中“3”对应的概率应该要比其他负标签类别高;而另一个“2”更类似于“7”,则这个这个样本的softmax输出值中“7”对应的概率应该比其他负标签类别高。这两个“2”对应的hard target是相同的,但是他们的soft target是不同的,soft target内蕴含着更多的信息。
Patient-KD
Patient-KD 算法综述
论文地址:Patient Knowledge Distillation for BERT Model Compression
图1: Vanilla KD和PKD比较
BERT预训练模型对资源的高需求导致其很难被应用在实际问题中,为缓解这个问题,论文中提出了Patient Knowledge Distillation(Patient KD)方法,将原始大模型压缩为同等有效的轻量级浅层网络。同时,作者对以往的知识蒸馏方法进行了调研,如图1所示,vanilla KD在QNLI和MNLI的训练集上可以很快的达到和teacher model相媲美的性能,但在测试集上则很快达到饱和。对此,作者提出一种假设,在知识蒸馏的过程中过拟合会导致泛化能力不良。为缓解这个问题,论文中提出一种“耐心”师生机制,即让Patient-KD中的学生模型从教师网络的多个中间层进行知识提取,而不是只从教师网络的最后一层输出中学习,该学习方法遵循以下两个策略:
-
PKD-Skip: 从每k层学习,假设教师网络的底层和高层中都包含重要信息,需要被学习到(如图2a所示)
-
PKD-Last: 从最后k层学习,假设教师网络越靠后的层包含越丰富的知识信息(如图2b所示)
图2a: PKD-Skip 学生网络学习教师网络每两层的输出 图2b: PKD-Last 学生网络从教师网络的最后六层学习
因为在BERT中仅使用最后一层的[CLS] token的输出来进行预测,且在其他BERT的变体模型中,如SDNet,是通过对每一层的[CLS] embedding的加权平均值进行处理并预测。由此可以推断,如果学生模型可以从任何教师网络中间层中的[CLS]表示中学习,那么它就有可能获得类似教师网络的泛化能力。
因此,Patient-KD中提出特殊的一种损失函数的计算方式:
其中,对于输入$x_i$,所有层的[CLS]的输出表示为: $h_i = [h{i,1}, h{i,2},..., h{i,k}] = BERT{k}(x_i) \in \mathbb{R}^{k\times d}$
$I{pt}$表示要从中提取知识的一组中间层,以从$BERT{12}$压缩到$BERT_6$为例,对于PKD-Skip策略,$I{pt} = {2,4,6,8,10}$;对于PKD-Last策略,$I{pt} = {7,8,9,10,11}$。M表示学生网络的层数,N是训练样本的数量,上标s和t分别代表学生网络和教师网络。
同时,Patient-KD中也使用了$L{DS}$和$L{CE}^S$两种损失函数用来衡量教师和学生网络的预测值的距离和学生网络在特定下游任务上的交叉熵损失。
最终的目标损失函数可以表示为:
实验结果
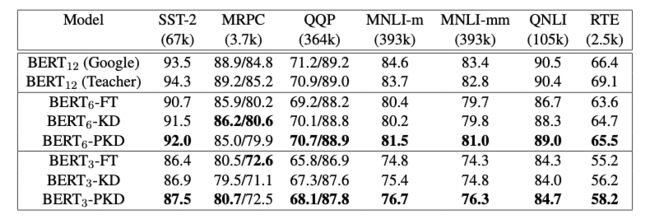
图3: results from the GLUE test server
作者将模型预测提交到GLUE并获得了在测试集上的结果,如图3所示。与fine-tuning和vanilla KD这两种方法相比,使用PKD训练的$BERT_3$和$BERT_6$在除MRPC外的几乎所有任务上都表现良好。其中,PKD代表Patient-KD-Skip方法。对于MNLI-m和MNLI-mm,六层模型比微调(FT)基线提高了1.1%和1.3%,
图4: PKD-Last 和 PKD-Skip 在GLUE基准上的对比
尽管这两种策略都比vanilla KD有所改进,但PKD-Skip的表现略好于PKD-Last。作者推测,这可能是由于每k层的信息提炼捕获了从低级到高级的语义,具备更丰富的内容和更多不同的表示,而只关注最后k层往往会捕获相对同质的语义信息。
图5: 参数量和推理时间对比
图5展示了$BERT_3$、$BERT_6$、$BERT_12$的推理时间即参数量, 实验表明Patient-KD方法实现了几乎线性的加速,$BERT_6$和$BERT_3$分别提速1.94倍和3.73倍。
DistilBERT
DistilBERT 算法综述
论文地址:DistilBERT, a distilled version of BERT: smaller, faster, cheaper and lighter
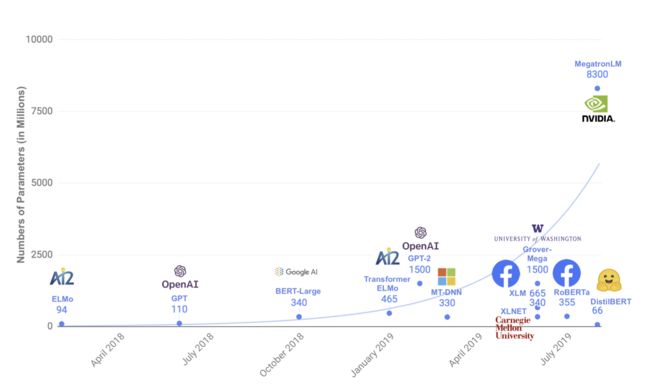
图1: 几个预训练模型的参数量统计
近年来,大规模预训练语言模型成为NLP任务的基本工具,虽然这些模型带来了显著的改进,但它们通常拥有数亿个参数(如图1所示),而这会引起两个问题。首先,大型预训练模型需要的计算成本很高。其次,预训练模型不断增长的计算和内存需求可能会阻碍语言处理应用的广泛落地。因此,作者提出DistilBERT,它表明小模型可以通过知识蒸馏从大模型中学习,并可以在许多下游任务中达到与大模型相似的性能,从而使其在推理时更轻、更快。
学生网络结构
学生网络DistilBERT具有与BERT相同的通用结构,但token-type embedding和pooler层被移除,层数减半。学生网络通过从教师网络中每两层抽取一层来进行初始化。
Training loss
L_{ce} 训练学生模仿教师模型的输出分布:
其中,t_i和s_i分别是教师网络和学生网络的预测概率。
同时使用了Hinton在2015年提出的softmax-temperature:
其中,T控制输出分布的平滑度,当T变大时,类别之间的差距变小;当T变小时,类别间的差距变大。z_i代表分类i的模型分数。在训练时对学生网络和教师网络使用同样的temperature T,在推理时,设置$T=1$,恢复为标准的softmax 最终的loss函数为L{ce}、Mask language model loss $L{mlm}$(参考BERT)和 cosine embedding loss $L_{cos}$(student和teacher隐藏状态向量的cos计算)的线性组合。
实验结果
图2:在GLUE数据集上的测试结果、下游任务测试和参数量对比
根据上图我们可以看到,DistilBERT与BERT相比减少了40%的参数,同时保留了BERT 97%的性能,但提高了60%的速度。
TinyBERT
TinyBERT 算法综述
论文地址:TinyBERT: Distilling BERT for Natural Language Understanding
TinyBERT是由华中科技大学和华为诺亚方舟实验室在2019年联合提出的一种针对transformer-based模型的知识蒸馏方法,以BERT为例对大型预训练模型进行研究。四层结构的 $TinyBERT{4}$ 在 GLUE benchmark 上可以达到 $BERT{base}$ 96.8%及以上的性能表现,同时模型缩小7.5倍,推理速度提升9.4倍。六层结构的 $TinyBERT{6}$ 可以达到和 $BERT{base}$ 同样的性能表现。
图1: TinyBERT learning
TinyBERT主要做了以下两点创新:
-
提供一种新的针对 transformer-based 模型进行蒸馏的方法,使得BERT中具有的语言知识可以迁移到TinyBERT中去。
-
提出一个两阶段学习框架,在预训练阶段和fine-tuning阶段都进行蒸馏,确保TinyBERT可以充分的从BERT中学习到一般领域和特定任务两部分的知识。
Transformer Distillation
假设TinyBERT有M层transformer layer,teacher BERT有N层transformer layer,则需要从teacher BERT的N层中抽取M层用于transformer层的蒸馏。$n = g(m)$ 定义了一个从学生网络到教师网络的映射关系,表示学生网络中第m层网络信息是从教师网络的第g(m)层学习到的,也就是教师网络的第n层。TinyBERT嵌入层和预测层也是从BERT的相应层学习知识的,其中嵌入层对应的指数为0,预测层对应的指数为M + 1,对应的层映射定义为 $0 = g(0)$ 和 $N + 1 = g(M + 1)$。在形式上,学生模型可以通过最小化以下的目标函数来获取教师模型的知识:
其中 $L{layer}$ 是给定的模型层的损失函数(比如transformer层或嵌入层),$f_m$ 代表第m层引起的行为函数,$\lambda{m}$ 表示第m层蒸馏的重要程度。
TinyBERT的蒸馏分为以下三个部分:transformer-layer distillation、embedding-layer distillation、prediction-layer distillation。
Transformer-layer distillation
Transformer-layer的蒸馏由attention based蒸馏和hidden states based蒸馏两部分组成。
图2: Transformer-layer distillation
其中,attention based蒸馏是受到论文Clack et al., 2019的启发,这篇论文中提到,BERT学习的注意力权重可以捕获丰富的语言知识,这些语言知识包括对自然语言理解非常重要的语法和共指信息。因此,TinyBERT提出attention based蒸馏,其目的是使学生网络很好地从教师网络处学习到这些语言知识。具体到模型中,就是让TinyBERT网络学习拟合BERT网络中的多头注意力矩阵,目标函数定义如下:
其中,$h$ 代表注意力头数,$A_i \in \mathbb{R}^{l\times l}$ 代表学生或教师的第 $i$ 个注意力头对应的注意力矩阵,$l$ 代表输入文本的长度。论文中提到,使用注意力矩阵 $A$ 而不是 $softmax(A)$ 是因为实验结果显示这样可以得到更快的收敛速度和更好的性能表现。
hidden states based蒸馏是对transformer层输出的知识进行了蒸馏处理,目标函数定义为:
其中,$H^S \in \mathbb{R}^{l \times d^{'}},\quad H^T \in \mathbb{R}^{l \times d}$ 分别代表学生网络和教师网络的隐状态,是FFN的输出。$d$ 和 $d^{'}$ 代表教师网络和学生网络的隐藏状态大小,且 $d^{'} < d$,因为学生网络总是小于教师网络。$W_h \in \mathbb{R}^{d^{'} \times d}$ 是一个可训练的线性变换矩阵,将学生网络的隐藏状态投影到教师网络隐藏状态所在的空间。
Embedding-layer Distillation
Embedding loss和hidden states loss同理,其中 $E^S,\quad E^T$ 代表学生网络和教师网络的嵌入,它们和隐藏状态矩阵的形状相同,同时 $W_e$ 和 $W_h$ 的作用也相同。
Prediction-layer Distillation
其中,$z^S, \quad z^T$ 分别是学生网络和教师网络预测的logits向量,$CE$ 代表交叉熵损失,$t$ 是temperature value,当 $t = 1$时,表现良好。
对上述三个部分的loss函数进行整合,则可以得到教师网络和学生网络之间对应层的蒸馏损失如下:
实验结果
图3: Results evaluated on GLUE benchmark
作者在GLUE基准上评估了TinyBERT的性能,模型大小、推理时间速度和准确率如图3所示。实验结果表明,TinyBERT在所有GLUE任务上都优于 $BERT{TINY}$,并在平均性能上获得6.8%的提升。这表明论文中提出的知识整理学习框架可以有效的提升小模型在下游任务中的性能。同时,$TinyBERT_4$ 以~4%的幅度显著的提升了KD SOTA基准线(比如,BERT-PKD和DistilBERT),参数缩小至~28%,推理速度提升3.1倍。与teacher $BERT{base}$ 相比,TinyBERT在保持良好性能的同时,模型缩小7.5倍,速度提升9.4倍。
DynaBERT
DynaBERT 算法综述
论文地址:DynaBERT: Dynamic BERT with Adaptive Width and Depth
近年的模型压缩方式基本上都是将大型的BERT网络压缩到一个固定的小尺寸网络。而实际工作中,不同的任务对推理速度和精度的要求不同,有的任务可能需要四层的压缩网络而有的任务会需要六层的压缩网络。DynaBERT(dynamic BERT)提出一种不同的思路,它可以通过选择自适应宽度和深度来灵活地调整网络大小,从而得到一个尺寸可变的网络。
DynaBERT的训练阶段包括两部分,首先通过知识蒸馏的方法将teacher BERT的知识迁移到有自适应宽度的子网络student $DynaBERT_W$中,然后再对 $DynaBERT_W$ 进行知识蒸馏得到同时支持深度自适应和宽度自适应的子网络 DynaBERT。训练过程流程图如图1所示。
图1: DynaBERT的训练过程
宽度自适应 Adaptive Width 一个标准的transformer中包含一个多头注意力(MHA)模块和一个前馈网络(FFN)。在论文中,作者通过变换注意力头的个数 $N_h$ 和前馈网络中中间层的神经元个数 $d{ff}$ 来更改transformer的宽度。同时定义一个缩放系数 $m_w$ 来进行剪枝,保留MHA中最左边的 $[m_wN_H]$ 个注意力头和 FFN中 $[m_wd{ff}]$ 个神经元。
为了充分利用网络的容量,更重要的头部或神经元应该在更多的子网络中共享。因此,在训练宽度自适应网络前,作者在 fine-tuned BERT网络中根据注意力头和神经元的重要性对它们进行了排序,然后在宽度方向上以降序进行排列。这种选取机制被称为 Network Rewiring。
图2: Network Rewiring
那么,要如何界定注意力头和神经元的重要性呢?作者参考 P. Molchanov et al., 2017 和 E. Voita et al., 2019 两篇论文提出,去掉某个注意力头或神经元前后的loss变化,就是该注意力头或神经元的重要程度,变化越大则越重要。
训练宽度自适应网络 首先,将BERT网络作为固定的教师网络,并初始化 $DynaBERT_W$。然后通过知识蒸馏将知识从教师网络迁移到 $DynaBERT_W$ 中不同宽度的学生子网络。其中,$m_w = [1.0, 0.75, 0.5, 0.25]$。
模型蒸馏的loss定义为:
其中, $\lambda_1, \lambda_2$ 是控制不同损失函数权重的参数, $l{pred}, l{emb}, l_{hidn}$ 分别定义为:
$l{pred}$ 代表预测层的loss,SCE 代表交叉熵损失函数。$l{emb}$ 代表嵌入层的loss,MSE代表均方差损失函数。$l_{hidn}$ 则为隐藏层的loss。
训练深度自适应网络 训练好宽度自适应的$DynaBERT_W$后,就可以将其作为教师网络训练同时具备宽度自适应和深度自适应的DynaBERT了。为了避免宽度方向上的灾难性遗忘,在每一轮训练中,仍对不同宽度进行训练。深度调节系数 $m_d$ 对网络层数进行调节,在训练中定义 $m_d = [1.0, 0.75, 0.5]$。深度方向上的剪枝根据 $mod(d+1, \frac{1}{1-m_d}) = 0$ 来去掉特定层,$d+1$ 是因为研究表明教师网络的最后一层知识很重要。
模型蒸馏的loss定义为:
实验结果
根据不同的宽度和深度剪裁系数,作者最终得到12个大小不同的DyneBERT模型,其在GLUE上的效果如下:
图3: results on GLUE benchmark
图4:Comparison of #parameters, FLOPs, latency on GPU and CPU between DynaBERT and DynaRoBERTa and other methods.
可以看到论文中提出的DynaBERT和DynaRoBERTa可以达到和 $BERT_{BASE}$ 及 $DynaRoBERTa$ 相当的精度,但是通常包含更少的参数,FLOPs或更低的延迟。在相同效率的约束下,从DynaBERT中提取的子网性能优于DistilBERT和TinyBERT。
使用DynaBERT训练策略压缩TinyBERT
下面我们将使用DynaBERT训练策略中宽度自适应部分对TinyBERT在GLUE基准数据集的QQP任务中进行蒸馏,验证实际效果。
实验环境
本实验使用aistudio至尊版GPU,cuda版本为10.1,具体依赖如下:
-
paddeslim使用develop版本
-
paddlenlp==2.0.0rc0
-
paddlepaddle-gpu==2.0.0.post101
# 配置实验环境
# cuda 10.1
!pip install paddlenlp==2.0.0rc0
!python -m pip install paddlepaddle-gpu==2.0.0.post101 -f https://paddlepaddle.org.cn/whl/mkl/stable.html
!pip install regexLooking in indexes: https://mirror.baidu.com/pypi/simple/ Collecting paddlenlp==2.0.0rc0
# 解压paddleslim和与训练模型
# 仅在第一次运行代码时使用
!tar -xf PaddleSlim-develop.tar
!tar -xf pretrained_model.tar
mv ./qqp_pretrained_model ./PaddleSlim-develop/demo/ofa/bert/
cd PaddleSlim-develop//home/aistudio/PaddleSlim-develop
import os
import time
import json
import random
import numpy as np
import paddle
import paddle.nn.functional as F
import paddlenlp.datasets as datasets
from functools import partial
from paddle.io import DataLoader
from paddlenlp.data import Stack, Tuple, Pad
from paddleslim.nas.ofa.utils import nlp_utils
from paddleslim.nas.ofa import OFA, DistillConfig, utils
from paddleslim.nas.ofa.convert_super import Convert, supernet
from paddle.metric import Metric, Accuracy, Precision, Recall
from paddlenlp.metrics import AccuracyAndF1, Mcc, PearsonAndSpearman
from paddlenlp.transformers import BertModel, BertForSequenceClassification, BertTokenizerTASK_CLASSES = {
"qqp": (datasets.GlueQQP, AccuracyAndF1),
}
MODEL_CLASSES = {"bert": (BertForSequenceClassification, BertTokenizer), }
def set_seed(args):
random.seed(args['seed'] + paddle.distributed.get_rank())
np.random.seed(args['seed'] + paddle.distributed.get_rank())
paddle.seed(args['seed'] + paddle.distributed.get_rank())数据集介绍
自然语言处理(NLP)主要包括自然语言理解(NLU)和自然语言生成(NLG)。为了推动通用和强大的自然语言理解系统的开发和研究,纽约大学、华盛顿大学和DeepMind联合创建了一个用于模型评估、比较和分析多个自然语言理解任务的在线平台,也就是GLUE(General Language Understanding Evaluation)。GLUE包括九项任务,分别是CoLA、SST-2、MRPC、STS-B、QQP、MNLI、QNLI、RTE和WNLI。它们可被分为三类,分别是单句分类任务、相似性和释义性任务和推理任务。
QQP
Quora Question Pairs2(QQP)数据集是来自社区问答网站Quora的问题对集合,任务是判断一对问题对是否等效,是一个二分类问题,结果是等效或不等效两种。QQP中的类别分布不平衡,其中63%是负样本,37%是正样本,衡量指标为准确率和F1值。
QQP数据集示列:
['What is the best self help book you have read? Why? How did it change your life?', 'What are the top self help books I should read?', '1'] 其中前两个句子为用来判断是否等效的句子,标签为1代表两个句子等效。
数据预处理
-
convert_example: 将QQP中的数据转化为可被模型处理的features
def convert_example(example,
tokenizer,
label_list,
max_seq_length=512,
is_test=False):
"""convert a glue example into necessary features"""
def _truncate_seqs(seqs, max_seq_length):
if len(seqs) == 1: # single sentence
# Account for [CLS] and [SEP] with "- 2"
seqs[0] = seqs[0][0:(max_seq_length - 2)]
else: # sentence pair
# Account for [CLS], [SEP], [SEP] with "- 3"
tokens_a, tokens_b = seqs
max_seq_length -= 3
while True: # truncate with longest_first strategy
total_length = len(tokens_a) + len(tokens_b)
if total_length <= max_seq_length:
break
if len(tokens_a) > len(tokens_b):
tokens_a.pop()
else:
tokens_b.pop()
return seqs
def _concat_seqs(seqs, separators, seq_mask=0, separator_mask=1):
concat = sum((seq + sep for sep, seq in zip(separators, seqs)), [])
segment_ids = sum(([i] * (len(seq) + len(sep)) for i, (sep, seq) in
enumerate(zip(separators, seqs))), [])
if isinstance(seq_mask, int):
seq_mask = [[seq_mask] * len(seq) for seq in seqs]
if isinstance(separator_mask, int):
separator_mask = [[separator_mask] * len(sep) for sep in separators]
p_mask = sum((s_mask + mask for sep, seq, s_mask, mask in
zip(separators, seqs, seq_mask, separator_mask)), [])
return concat, segment_ids, p_mask
if not is_test:
# `label_list == None` is for regression task
label_dtype = "int64" if label_list else "float32"
# get the label
label = example[-1]
example = example[:-1]
#create label maps if classification task
if label_list:
label_map = {}
for (i, l) in enumerate(label_list):
label_map[l] = i
label = label_map[label]
label = np.array([label], dtype=label_dtype)
# tokenize raw text
tokens_raw = [tokenizer(l) for l in example]
# truncate to the truncate_length,
tokens_trun = _truncate_seqs(tokens_raw, max_seq_length)
# concate the sequences with special tokens
tokens_trun[0] = [tokenizer.cls_token] + tokens_trun[0]
tokens, segment_ids, _ = _concat_seqs(tokens_trun, [[tokenizer.sep_token]] *
len(tokens_trun))
# convert the token to ids
input_ids = tokenizer.convert_tokens_to_ids(tokens)
valid_length = len(input_ids)
# The mask has 1 for real tokens and 0 for padding tokens. Only real
# tokens are attended to.
# input_mask = [1] * len(input_ids)
if not is_test:
return input_ids, segment_ids, valid_length, label
else:
return input_ids, segment_ids, valid_length以QQP train dataset中第七条数据为例,对每一步数据处理的结果进行展示。
代码:
train_ds = dataset_class.get_datasets(['train'])
exp = train_ds[7]
print('QQP train example: ', exp)
tokens_raw = [tokenizer(l) for l in exp]
print('tokens of this example: ', tokens_raw)
tokens_trun = _truncate_seqs(tokens_raw[:2], 128)
tokens_trun[0] = [tokenizer.cls_token] + tokens_trun[0]
print('tokens after _truncate_seqs: ', tokens_trun)
tokens, segment_ids, pmask = _concat_seqs(tokens_trun, [[tokenizer.sep_token]] * len(tokens_trun))
print('tokens after _concat_seqs: ', tokens)
print('segments_ids: ', segment_ids)
print('pmask: ', pmask)
input_ids = tokenizer.convert_tokens_to_ids(tokens)
print('input ids: ', input_ids)
valid_length = len(input_ids)
print('input ids length: ', valid_length)对应的print结果:
QQP train example: ['What is the best self help book you have read? Why? How did it change your life?', 'What are the top self help books I should read?', '1'] tokens of this example: [['what', 'is', 'the', 'best', 'self', 'help', 'book', 'you', 'have', 'read', '?', 'why', '?', 'how', 'did', 'it', 'change', 'your', 'life', '?'], ['what', 'are', 'the', 'top', 'self', 'help', 'books', 'i', 'should', 'read', '?'], ['1']] tokens after _truncate_seqs: [['[CLS]', 'what', 'is', 'the', 'best', 'self', 'help', 'book', 'you', 'have', 'read', '?', 'why', '?', 'how', 'did', 'it', 'change', 'your', 'life', '?'], ['what', 'are', 'the', 'top', 'self', 'help', 'books', 'i', 'should', 'read', '?']] tokens after _concat_seqs: ['[CLS]', 'what', 'is', 'the', 'best', 'self', 'help', 'book', 'you', 'have', 'read', '?', 'why', '?', 'how', 'did', 'it', 'change', 'your', 'life', '?', '[SEP]', 'what', 'are', 'the', 'top', 'self', 'help', 'books', 'i', 'should', 'read', '?', '[SEP]'] segments_ids: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] pmask: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1] input ids: [101, 2054, 2003, 1996, 2190, 2969, 2393, 2338, 2017, 2031, 3191, 1029, 2339, 1029, 2129, 2106, 2009, 2689, 2115, 2166, 1029, 102, 2054, 2024, 1996, 2327, 2969, 2393, 2808, 1045, 2323, 3191, 1029, 102] input ids length: 34
模型构建
### reorder weights according head importance and neuron importance
def reorder_neuron_head(model, head_importance, neuron_importance):
# reorder heads and ffn neurons
for layer, current_importance in enumerate(neuron_importance):
# reorder heads
idx = paddle.argsort(head_importance[layer], descending=True)
nlp_utils.reorder_head(model.bert.encoder.layers[layer].self_attn, idx)
# reorder neurons
idx = paddle.argsort(
paddle.to_tensor(current_importance), descending=True)
nlp_utils.reorder_neuron(
model.bert.encoder.layers[layer].linear1.fn, idx, dim=1)
nlp_utils.reorder_neuron(
model.bert.encoder.layers[layer].linear2.fn, idx, dim=0)
def soft_cross_entropy(inp, target):
inp_likelihood = F.log_softmax(inp, axis=-1)
target_prob = F.softmax(target, axis=-1)
return -1. * paddle.mean(paddle.sum(inp_likelihood * target_prob, axis=-1))
def evaluate(model, criterion, metric, data_loader, epoch, step,
width_mult=1.0):
with paddle.no_grad():
model.eval()
metric.reset()
for batch in data_loader:
input_ids, segment_ids, labels = batch
logits = model(input_ids, segment_ids, attention_mask=[None, None])
if isinstance(logits, tuple):
logits = logits[0]
loss = criterion(logits, labels)
correct = metric.compute(logits, labels)
metric.update(correct)
results = metric.accumulate()
print("epoch: %d, batch: %d, width_mult: %s, eval loss: %f, %s: %s\n" %
(epoch, step, 'teacher' if width_mult == 100 else str(width_mult),
loss.numpy(), metric.name(), results))
model.train()
### monkey patch for bert forward to accept [attention_mask, head_mask] as attention_mask
def bert_forward(self,
input_ids,
token_type_ids=None,
position_ids=None,
attention_mask=[None, None]):
wtype = self.pooler.dense.fn.weight.dtype if hasattr(
self.pooler.dense, 'fn') else self.pooler.dense.weight.dtype
if attention_mask[0] is None:
attention_mask[0] = paddle.unsqueeze(
(input_ids == self.pad_token_id).astype(wtype) * -1e9, axis=[1, 2])
embedding_output = self.embeddings(
input_ids=input_ids,
position_ids=position_ids,
token_type_ids=token_type_ids)
encoder_outputs = self.encoder(embedding_output, attention_mask)
sequence_output = encoder_outputs
pooled_output = self.pooler(sequence_output)
return sequence_output, pooled_output
BertModel.forward = bert_forward
def print_arguments(args):
"""print arguments"""
print('----------- Configuration Arguments -----------')
for arg, value in sorted(args.items()):
print('%s: %s' % (arg, value))
print('------------------------------------------------')
args = {'task_name': 'QQP',
'model_type': 'bert',
'model_name_or_path': './demo/ofa/bert/qqp_pretrained_model/',
'seed': 42,
'n_gpu': 1,
'max_seq_length': 128,
'batch_size': 32,
'learning_rate': 2e-5,
'num_train_epochs': 3,
'warmup_steps': 0,
'max_steps': -1,
'adam_epsilon': 1e-8,
'weight_decay': 0.0,
'lambda_logit': 1.0,
'logging_steps': 10,
'output_dir': './demo/ofa/bert/tmp/QQP/',
'save_steps': 500,
'width_mult_list': [1.0, 0.8333333333333334, 0.6666666666666666, 0.5],
}
print_arguments(args)----------- Configuration Arguments ----------- adam_epsilon: 1e-08 batch_size: 32 lambda_logit: 1.0 learning_rate: 2e-05 logging_steps: 10 max_seq_length: 128 max_steps: -1 model_name_or_path: ./demo/ofa/bert/qqp_pretrained_model/ model_type: bert n_gpu: 1 num_train_epochs: 3 output_dir: ./demo/ofa/bert/tmp/QQP/ save_steps: 500 seed: 42 task_name: QQP warmup_steps: 0 weight_decay: 0.0 width_mult_list: [1.0, 0.8333333333333334, 0.6666666666666666, 0.5] ------------------------------------------------paddle.set_device("gpu") if paddle.distributed.get_world_size() > 1: paddle.distributed.init_parallel_env() set_seed(args) args['task_name'] = args['task_name'].lower() dataset_class, metric_class = TASK_CLASSES[args['task_name']] model_class, tokenizer_class = MODEL_CLASSES[args['model_type']] train_ds = dataset_class.get_datasets(['train']) tokenizer = tokenizer_class.from_pretrained(args['model_name_or_path']) # Constructs a BERT tokenizer. It uses a basic tokenizer to do punctuation splitting, lower casing and so on, # and follows a WordPiece tokenizer to tokenize as subwords. trans_func = partial( convert_example, tokenizer=tokenizer, label_list=train_ds.get_labels(), max_seq_length=args['max_seq_length']) train_ds = train_ds.apply(trans_func, lazy=True) train_batch_sampler = paddle.io.DistributedBatchSampler( train_ds, batch_size=args['batch_size'], shuffle=True) batchify_fn = lambda samples, fn=Tuple( Pad(axis=0, pad_val=tokenizer.pad_token_id), # input Pad(axis=0, pad_val=tokenizer.pad_token_id), # segment Stack(), # length Stack(dtype="int64" if train_ds.get_labels() else "float32") # label ): [data for i, data in enumerate(fn(samples)) if i != 2] train_data_loader = DataLoader( dataset=train_ds, batch_sampler=train_batch_sampler, collate_fn=batchify_fn, num_workers=0, return_list=True) dev_dataset = dataset_class.get_datasets(["dev"]) dev_dataset = dev_dataset.apply(trans_func, lazy=True) dev_batch_sampler = paddle.io.BatchSampler( dev_dataset, batch_size=args['batch_size'], shuffle=False) dev_data_loader = DataLoader( dataset=dev_dataset, batch_sampler=dev_batch_sampler, collate_fn=batchify_fn, num_workers=0, return_list=True) num_labels = 1 if train_ds.get_labels() == None else len( train_ds.get_labels()) model = model_class.from_pretrained( args['model_name_or_path'], num_classes=num_labels) if paddle.distributed.get_world_size() > 1: model = paddle.DataParallel(model)100%|██████████| 40719/40719 [00:01<00:00, 26854.93it/s]
模型训练
# Step1: Initialize a dictionary to save the weights from the origin BERT model.
origin_weights = {}
for name, param in model.named_parameters():
origin_weights[name] = param
# Step2: Convert origin model to supernet.
sp_config = supernet(expand_ratio=args['width_mult_list'])
model = Convert(sp_config).convert(model)
# Use weights saved in the dictionary to initialize supernet.
utils.set_state_dict(model, origin_weights)
del origin_weights
# Step3: Define teacher model.
teacher_model = model_class.from_pretrained(
args['model_name_or_path'], num_classes=num_labels)
# Step4: Config about distillation.
mapping_layers = ['bert.embeddings']
for idx in range(model.bert.config['num_hidden_layers']):
mapping_layers.append('bert.encoder.layers.{}'.format(idx))
default_distill_config = {
'lambda_distill': 0.1, # 蒸馏loss的缩放比例
'teacher_model': teacher_model,
'mapping_layers': mapping_layers,
}
distill_config = DistillConfig(**default_distill_config)
# Step5: Config in supernet training.
ofa_model = OFA(model,
distill_config=distill_config,
elastic_order=['width'])
criterion = paddle.nn.loss.CrossEntropyLoss() if train_ds.get_labels(
) else paddle.nn.loss.MSELoss()
metric = metric_class()
# Step6: Calculate the importance of neurons and head,
# and then reorder them according to the importance.
head_importance, neuron_importance = nlp_utils.compute_neuron_head_importance(
args['task_name'],
ofa_model.model,
dev_data_loader,
loss_fct=criterion,
num_layers=model.bert.config['num_hidden_layers'],
num_heads=model.bert.config['num_attention_heads'])
reorder_neuron_head(ofa_model.model, head_importance, neuron_importance)
lr_scheduler = paddle.optimizer.lr.LambdaDecay(
args['learning_rate'],
lambda current_step, num_warmup_steps=args['warmup_steps'],
num_training_steps=args['max_steps'] if args['max_steps'] > 0 else
(len(train_data_loader) * args['num_train_epochs']): float(
current_step) / float(max(1, num_warmup_steps))
if current_step < num_warmup_steps else max(
0.0,
float(num_training_steps - current_step) / float(
max(1, num_training_steps - num_warmup_steps))))
optimizer = paddle.optimizer.AdamW(
learning_rate=lr_scheduler,
epsilon=args['adam_epsilon'],
parameters=ofa_model.model.parameters(),
weight_decay=args['weight_decay'],
apply_decay_param_fun=lambda x: x in [
p.name for n, p in ofa_model.model.named_parameters()
if not any(nd in n for nd in ["bias", "norm"])
])
global_step = 0
tic_train = time.time()
for epoch in range(args['num_train_epochs']):
# Step7: Set current epoch and task.
ofa_model.set_epoch(epoch)
ofa_model.set_task('width')
for step, batch in enumerate(train_data_loader):
global_step += 1
input_ids, segment_ids, labels = batch
for width_mult in args['width_mult_list']:
# Step8: Broadcast supernet config from width_mult,
# and use this config in supernet training.
net_config = utils.dynabert_config(ofa_model, width_mult)
ofa_model.set_net_config(net_config)
logits, teacher_logits = ofa_model(
input_ids, segment_ids, attention_mask=[None, None])
rep_loss = ofa_model.calc_distill_loss()
logit_loss = soft_cross_entropy(logits,
teacher_logits.detach())
loss = rep_loss + args['lambda_logit'] * logit_loss
loss.backward()
optimizer.step()
lr_scheduler.step()
ofa_model.model.clear_gradients()
if global_step % args['logging_steps'] == 0:
if (not args['n_gpu'] > 1) or paddle.distributed.get_rank() == 0:
print(
"global step %d, epoch: %d, batch: %d, loss: %f, speed: %.2f step/s"
% (global_step, epoch, step, loss,
args['logging_steps'] / (time.time() - tic_train)))
tic_train = time.time()
if global_step % args['save_steps'] == 0:
tic_eval = time.time()
evaluate(
teacher_model,
criterion,
metric,
dev_data_loader,
epoch,
step,
width_mult=100)
print("eval done total : %s s" %
(time.time() - tic_eval))
for idx, width_mult in enumerate(args['width_mult_list']):
net_config = utils.dynabert_config(ofa_model, width_mult)
ofa_model.set_net_config(net_config)
tic_eval = time.time()
acc = evaluate(ofa_model, criterion, metric,
dev_data_loader, epoch, step, width_mult)
print("eval done total : %s s" %
(time.time() - tic_eval))
if (not args['n_gpu'] > 1
) or paddle.distributed.get_rank() == 0:
output_dir = os.path.join(args['output_dir'],
"model_%d" % global_step)
if not os.path.exists(output_dir):
os.makedirs(output_dir)
# need better way to get inner model of DataParallel
model_to_save = model._layers if isinstance(
model, paddle.DataParallel) else model
model_to_save.save_pretrained(output_dir)
tokenizer.save_pretrained(output_dir)/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/fluid/dataloader/dataloader_iter.py:354: DeprecationWarning: `np.object` is a deprecated alias for the builtin `object`. To silence this warning, use `object` by itself. Doing this will not modify any behavior and is safe. Deprecated in NumPy 1.20; for more details and guidance: https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations if arr.dtype == np.object:global step 34110, epoch: 2, batch: 11367, loss: 0.148229, speed: 5.31 step/s
训练结果:best model 32500
| WIDTH | ACCURACY | F1 |
|---|---|---|
| Teacher | 0.9047 | 0.8751 |
| 1 | 0.9069 | 0.8776 |
| 0.83334 | 0.9055 | 0.8756 |
| 0.66667 | 0.8992 | 0.8678 |
| 0.5 | 0.8967 | 0.8645 |
| TASK | METRIC | TINYBERT(L=4, D=312) | RESULT WITH OFA |
|---|---|---|---|
| QQP | Accuracy/F1 | 0.9047/0.8751 | 0.9021/0.8714 |
导出子模型
注意:运行下面一段代码时需重启环境
import os
import random
import time
import json
from functools import partial
import numpy as np
import paddle
import paddle.nn as nn
import paddle.nn.functional as F
from paddlenlp.transformers import BertModel, BertForSequenceClassification, BertTokenizer
from paddlenlp.utils.log import logger
from paddleslim.nas.ofa import OFA, utils
from paddleslim.nas.ofa.convert_super import Convert, supernet
from paddleslim.nas.ofa.layers import BaseBlock
MODEL_CLASSES = {"bert": (BertForSequenceClassification, BertTokenizer), }def export_static_model(model, model_path, max_seq_length):
input_shape = [
paddle.static.InputSpec(
shape=[None, max_seq_length], dtype='int64'),
paddle.static.InputSpec(
shape=[None, max_seq_length], dtype='int64')
]
net = paddle.jit.to_static(model, input_spec=input_shape)
paddle.jit.save(net, model_path)
def do_train(args):
paddle.set_device("gpu")
model_class, tokenizer_class = MODEL_CLASSES[args['model_type']]
config_path = os.path.join(args['model_name_or_path'], 'model_config.json')
cfg_dict = dict(json.loads(open(config_path).read()))
num_labels = cfg_dict['num_classes']
model = model_class.from_pretrained(
args['model_name_or_path'], num_classes=num_labels)
origin_model = model_class.from_pretrained(
args['model_name_or_path'], num_classes=num_labels)
sp_config = supernet(expand_ratio=[1.0, args['width_mult']])
model = Convert(sp_config).convert(model)
ofa_model = OFA(model)
sd = paddle.load(
os.path.join(args['model_name_or_path'], 'model_state.pdparams'))
ofa_model.model.set_state_dict(sd)
best_config = utils.dynabert_config(ofa_model, args['width_mult'])
ofa_model.export(
best_config,
input_shapes=[[1, args['max_seq_length']], [1, args['max_seq_length']]],
input_dtypes=['int64', 'int64'],
origin_model=origin_model)
for name, sublayer in origin_model.named_sublayers():
if isinstance(sublayer, paddle.nn.MultiHeadAttention):
sublayer.num_heads = int(args['width_mult'] * sublayer.num_heads)
output_dir = os.path.join(args['sub_model_output_dir'],
"model_width_%.5f" % args['width_mult'])
if not os.path.exists(output_dir):
os.makedirs(output_dir)
model_to_save = origin_model
model_to_save.save_pretrained(output_dir)
if args['static_sub_model'] != None:
export_static_model(origin_model, args['static_sub_model'],
args['max_seq_length'])
sub_args = {'model_name_or_path': './demo/ofa/bert/tmp/QQP/model_32500/',
'max_seq_length': 128,
'sub_model_output_dir': './demo/ofa/bert/tmp/QQP/dynamic_model/',
'static_sub_model': './demo/ofa/bert/tmp/QQP/static_model',
'width_mult':0.5}
args.update(sub_args)
print_arguments(args)----------- Configuration Arguments ----------- adam_epsilon: 1e-08 batch_size: 32 lambda_logit: 1.0 learning_rate: 2e-05 logging_steps: 10 max_seq_length: 128 max_steps: -1 model_name_or_path: ./demo/ofa/bert/tmp/QQP/model_32500/ model_type: bert n_gpu: 1 num_train_epochs: 3 output_dir: ./demo/ofa/bert/tmp/QQP/ save_steps: 500 seed: 42 static_sub_model: ./demo/ofa/bert/tmp/QQP/static_model sub_model_output_dir: ./demo/ofa/bert/tmp/QQP/dynamic_model/ task_name: QQP warmup_steps: 0 weight_decay: 0.0 width_mult: 0.6666666666666666 width_mult_list: [1.0, 0.8333333333333334, 0.6666666666666666, 0.5] ------------------------------------------------
可以看到导出的模型由84.6M降低至72.7M,模型参数大小减小
项目实战地址:
| 【实践】预训练模型蒸馏 -- 宽度自适应策略蒸馏TinyBERT - 飞桨AI Studio - 人工智能学习与实训社区 |