读《趣学算法》：重开算法之门，神奇的兔子数列（斐波那契数列）

14天阅读挑战赛

系列文章

第1篇：读《趣学算法》：重开算法之门，时间复杂度与空间复杂度

1. 前言

继续读《趣学算法》，这一节，读到了神奇的兔子数列，让我们将算法的改进，进行到底~。

2. 神奇的兔子数列（斐波那契数列）

描述：假设有一对出生的兔子，第二个月进入成熟期，第三个月开始生育兔子，而每对兔子每月能生一对兔子，兔子永不会死去，……，那么由第一对兔子开始，12个月后会有多少对兔子呢？

3. 问题分析

第1个月：1对A新生兔子 （总计1对）
第2个月：1对A成熟的兔子 （总计1对）
第3个月：1对A成熟的兔子+1对AB新生兔子 （总计2对）
第4个月：1对A成熟的兔子+1对AC新生兔子+1对AB成熟兔子 （总计3对）
第5个月： 1对A成熟的兔子+1对AD新生兔子+1对AC成熟兔子+1对AB成熟兔子+ABA新生兔子（总计5对）
第6个月：1对A成熟+1对AE新生+1对AD成熟+1对AC成熟+1对ACA新生+1对AB成熟+1对ABB新生+1对ABA成熟 （总计8对）
第7个月：1对A成熟+1对AF新生+1对AE成熟+1对AD成熟+1对ADA新生+1对AC成熟+1对ACB新生+1对ACA成熟+1对AB成熟+1对ABC新生+1对ABB成熟+1对ABA成熟+1对ABAA新生 （总计13对）
……

从1月开始……第7月依次为：1对、1对、2对、3对、5对、8对、13对

所以可知：从第3个月开始（包含第3个月），之后第n个月兔子的数量是是(n-1)+(n-2)对，列出函数为：

$$f(n)=\{\begin{array}{ll}1& n<2\\ f(n-1)+f(n-2)& n\ge 3\end{array}$$

由此可知，最直接的算法，可以通过递归函数来实现

4. 递归算法：青铜

提示：简单描述算法知识点相关题目题意

4.1 算法实现

#include
#include

int fib(int n)
{
   if(n <= 2)
   {
     printf("n=%d, 有(%d)对兔子, \n", n, 1);	   
     return 1;
   }
   else
   {
     int sum = fib(n-1) + fib(n-2);
     printf("n=%d, 有(%d)对兔子, \n", n, sum);
     return sum;
   }  

}


int main(int argc, char **argv)
{

    int n = atoi(argv[1]);
    printf("计算斐波那契数列，第%d个月有多少个兔子？ \n", n);
    
    int sum = fib(n);
    printf("总计:%d对\n", sum);
    return 0;
}

4.2 运行结果

• 如下，运行结果与我们第2节问题分析的情况是一致的。第7个月将有13对兔子。

szhou@bc04:~/Test$ gcc -o fib Fibonacci.c          
szhou@bc04:~/Test$ ./fib 7
计算斐波那契数列，第7个月有多少个兔子？ 
n=2, 有(1)对兔子, 
n=1, 有(1)对兔子, 
n=3, 有(2)对兔子, 
n=2, 有(1)对兔子, 
n=4, 有(3)对兔子, 
n=2, 有(1)对兔子, 
n=1, 有(1)对兔子, 
n=3, 有(2)对兔子, 
n=5, 有(5)对兔子, 
n=2, 有(1)对兔子, 
n=1, 有(1)对兔子, 
n=3, 有(2)对兔子, 
n=2, 有(1)对兔子, 
n=4, 有(3)对兔子, 
n=6, 有(8)对兔子, 
n=2, 有(1)对兔子, 
n=1, 有(1)对兔子, 
n=3, 有(2)对兔子, 
n=2, 有(1)对兔子, 
n=4, 有(3)对兔子, 
n=2, 有(1)对兔子, 
n=1, 有(1)对兔子, 
n=3, 有(2)对兔子, 
n=5, 有(5)对兔子, 
n=7, 有(13)对兔子, 
总计:13对
szhou@bc04:~/Test$ 

• 改变参数，求第12个月，如下可得$f(12)=144$对兔子

szhou@bc04:~/Test$ ./fib 12
计算斐波那契数列，第12个月有多少个兔子？ 
……省略……
n=12, 有(144)对兔子, 
总计:144对
szhou@bc04:~/Test$ 

4.3 时间复杂度：O( $2^{n/2}$)

4.3.1 回顾算法

int fib(int n)
{
   if(n <= 2)
   {
     printf("n=%d, 有(%d)对兔子, \n", n, 1);	   
     return 1;
   }
   else
   {
     int sum = fib(n-1) + fib(n-2);
     printf("n=%d, 有(%d)对兔子, \n", n, sum);
     return sum;
   }  
}

4.3.2 分析方法

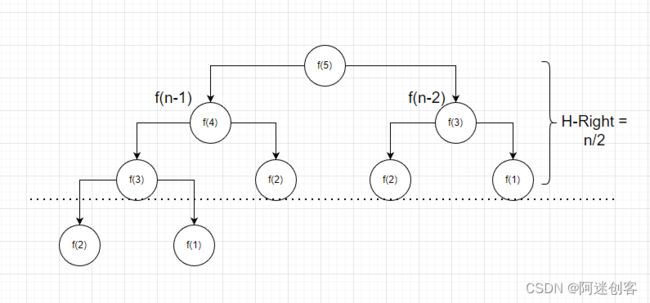
分析int fib(int n)这个递归函数的方法，其一是按照高等数学的方法，求出斐波那契数列的通项公式，这个对于我来说，忘得太干净。还是走第二条路，画出此函数的计算过程，可以发现它是一个树，可以称之为递归树，下面的每一个圈圈，都是一次计算！为了推导方便，假设n=5。

• 假设 n = 5
• 左侧树每次递减1，递减直到2为止，即$h_1=n-1$，此处为4
• 右侧树每次递减2，递减直到2或1为止，即$h_2=n/2$，此处为3
• 可以发现，在$h_2=n/2$的部分，是满二叉树，这部分的节点数为 $2^{n/2}-1$，这是一个指数函数，计算次数会呈爆炸性增长，这不是我们想要的
• 备注：在下图虚线下的部分，即左侧树，也只有2个节点未计入，在时间复杂度计算中，可以忽略

分析结果：时间复杂度可表示为 O( $2^{n/2}$)

5.算法改进：白银

改进思路：从斐波那契数列的特点，从第3项开始，后面每一项都是前两项的和，我们可以做一个数组，将每次的计算结果都存储起来，这样只需要执行大约n次，即可达到结果。

5.1 代码实现

#include
#include

int fib_pro(int n)
{
    int *p = malloc(sizeof(int) * (n+1));  //计算1次  
    p[1] = 1; //计算1次
    p[2] = 1; //计算1次   
    for(int i=3; i<=n; i++) 
    {
         p[i]=p[i-1]+p[i-2];  //计算n-2次
    }
    return p[n];
}

int main(int argc, char **argv)
{

    int n = atoi(argv[1]);
    printf("计算斐波那契数列，改进型算法，第%d个月有多少个兔子？ \n", n);
    
    int sum = fib_pro(n);
    printf("总计:%d对\n", sum);
    return 0;
}

5.2 时间复杂度: $O(n)$

• 仅关注核心循环部分，可得 $T(n)=n-2$，当$n$很大的时候，可以约等于$n$
• 所以此次改进的算法复杂度可表示为：$O(n)$

5.3 运算结果

szhou@bc04:~/Test$ gcc -o fib_pro Fibonacci.c 
szhou@bc04:~/Test$ ./fib_pro 7
计算斐波那契数列，改进型算法，第7个月有多少个兔子？ 
总计:13对
szhou@bc04:~/Test$ ./fib_pro 12
计算斐波那契数列，改进型算法，第12个月有多少个兔子？ 
总计:144对
szhou@bc04:~/Test$ 

6. 再次改进：能是王者？

从楼上改进算法，我们创建了一个n+1的数组空间，但其实我们只需要最后一个值，所以我们还可以对存储空间，即算法的空间复杂度做一下改进，将空间复杂度从$O(n)$降低为$O(1)$

#include
#include

int fib_xPro(int n)
{
    int temp_1 = 1;
    int temp_2 = 1;
    int temp_3 = 1;

    for(int i=3; i<=n; i++)
    {         
         temp_3 = temp_1 + temp_2;
         temp_1 = temp_2;
         temp_2 = temp_3;
    }
    return temp_3;
}

int main(int argc, char **argv)
{

    int n = atoi(argv[1]);
    printf("计算斐波那契数列，改进型算法，第%d个月有多少个兔子？ \n", n);
    
    int sum = fib_xPro(n);
    printf("总计:%d对\n", sum);
    return 0;
}

szhou@bc04:~/Test$ gcc -o fib_xPro Fibonacci.c     
szhou@bc04:~/Test$ ./fib_xPro 7
计算斐波那契数列，改进型算法，第7个月有多少个兔子？ 
总计:13对
szhou@bc04:~/Test$ ./fib_xPro 12
计算斐波那契数列，改进型算法，第12个月有多少个兔子？ 
总计:144对
szhou@bc04:~/Test$ 

7. 结尾语

如有错误，帮忙指正一下哈~