多类感知器算法
多类感知器算法
1.1 题目的主要研究内容
- 用多类感知器算法用多类感知器算法求下列模式的判别函数:
W1:X1=[-1,-1];
W2:X2=[0,0];
W3:X3=[1,1];
1.2 题目研究的工作基础或实验条件
- 软件环境
本次仿真所用的软件为Anaonda,在Anaconda navigator中启动jupyter Notebook,它是一个基于网页的交互式计算环境,本身支持多种语言的开发,用它编写python代码,实现仿真要求。
1.3 设计思想
①写出所给模式类别的增广矩阵形式,选定权向量W的初值和校正增量C;
②在第k次迭代时,一个属于W类的模式样本 X 被送入分类器,计算所有判别函数:d(k)=W(k) X ; j =1,2,3,.........,M;
③若d(k)>d(k), 对于任意的j≠i,j=1,2,3,.....,M 则权向量不变:
W(k+1)=W(k), j =1,2,3.......M;
④若第l个权向量使得d(k)≤d(k),则相应的权向量作调整,即:
W(k+1)=W(k)+Cx
W(k+1)=W(k)-Cx
W(k+1)=W(k)+Cx,j≠i,l
经过有限次迭代后,会一直满足d(k)>d(k),可见上图手动推演结果,则此时的样本已正确分类,此时的权向量即为所求,判别函数也可以由权向量推出。
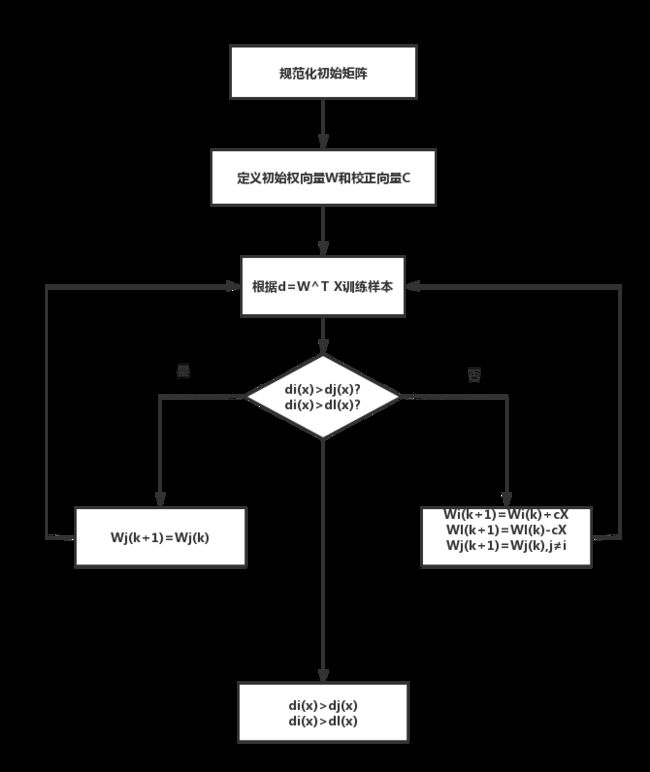
1.4 流程图
如图1-4所示:
1.5 主要程序代码
import numpy as np
x1 = np.mat([-1,-1,1])
x2 = np.mat([0,0,1])
x3 = np.mat([1,1,1]) %定义训练样本
x = [x1.T,x2.T,x3.T] %将训练样本放入三维矩阵
w1 = np.mat([0,0,0])
w2 = np.mat([0,0,0])
w3 = np.mat([0,0,0]) %定义初始权向量
w = [w1.T,w2.T,w3.T] %将权向量转置
w4 = [w1,w2,w3] %放入三维矩阵
f = True %标志位f=ture进入循环
count = 0 %定义迭代次数
while f:
f = False
for i in range(len(x)): %确定循环次数
count += 1
d = [] %定义为空矩阵
for j in range(len(w)):%确定j的循环次数
d.append(w[j].T * x[i])
print(d)
print(w4)
if (count % 3 == 1): %count/3取余判断下标
if d[0] <= d[1] and d[0] <= d[2]:
w[0] += x[0] %更新权向量
w[1] -= x[0]
w[2] -= x[0]
f = True %标志位
elif d[0] > d[1] and d[0] <= d[2]: %判断d的下标
w[1] = w[1] %更新权向量
w[0] += x[0]
w[2] -= x[0]
elif d[0] > d[2] and d[0] <= d[1]: %判断d的下标
w[0] -= x[0] %更新权向量
w[2] = w[2]
w[1] += x[0]
# d = np.array(d)
if(count%3==2):
if d[1] <= d[0] and d[1] <= d[2]:
w[0] -= x[1]
w[1] += x[1]
w[2] -= x[1]
elif d[1] > d[0] and [1] <= d[2]:
w[0] = w[0]
w[1] += x[1]
w[2] -= x[1]
elif d[1] > d[2] and d[1] <= d[0]:
w[0] -= x[1]
w[2] = w[2]
w[1] += x[1]
if(count%3==0):
if d[2] <= d[1] and d[2] <= d[0]:
w[0] -= x[2]
w[1] -= x[2]
w[2] += x[2]
elif d[2] > d[0] and d[2] <= d[1]:
w[0] = w[0]
w[1] -= x[2]
w[2] += x[2]
elif d[2] > d[1] and d[2] <= d[0]:
w[0] -= x[2]
w[1] = w[1]
w[2] += x[2]
print(w)
1.5 主要程序代码
import numpy as np
x1 = np.mat([-1,-1,1])
x2 = np.mat([0,0,1])
x3 = np.mat([1,1,1]) %定义训练样本
x = [x1.T,x2.T,x3.T] %将训练样本放入三维矩阵
w1 = np.mat([0,0,0])
w2 = np.mat([0,0,0])
w3 = np.mat([0,0,0]) %定义初始权向量
w = [w1.T,w2.T,w3.T] %将权向量转置
w4 = [w1,w2,w3] %放入三维矩阵
f = True %标志位f=ture进入循环
count = 0 %定义迭代次数
while f:
f = False
for i in range(len(x)): %确定循环次数
count += 1
d = [] %定义为空矩阵
for j in range(len(w)):%确定j的循环次数
d.append(w[j].T * x[i])
print(d)
print(w4)
if (count % 3 == 1): %count/3取余判断下标
if d[0] <= d[1] and d[0] <= d[2]:
w[0] += x[0] %更新权向量
w[1] -= x[0]
w[2] -= x[0]
f = True %标志位
elif d[0] > d[1] and d[0] <= d[2]: %判断d的下标
w[1] = w[1] %更新权向量
w[0] += x[0]
w[2] -= x[0]
elif d[0] > d[2] and d[0] <= d[1]: %判断d的下标
w[0] -= x[0] %更新权向量
w[2] = w[2]
w[1] += x[0]
# d = np.array(d)
if(count%3==2):
if d[1] <= d[0] and d[1] <= d[2]:
w[0] -= x[1]
w[1] += x[1]
w[2] -= x[1]
elif d[1] > d[0] and [1] <= d[2]:
w[0] = w[0]
w[1] += x[1]
w[2] -= x[1]
elif d[1] > d[2] and d[1] <= d[0]:
w[0] -= x[1]
w[2] = w[2]
w[1] += x[1]
if(count%3==0):
if d[2] <= d[1] and d[2] <= d[0]:
w[0] -= x[2]
w[1] -= x[2]
w[2] += x[2]
elif d[2] > d[0] and d[2] <= d[1]:
w[0] = w[0]
w[1] -= x[2]
w[2] += x[2]
elif d[2] > d[1] and d[2] <= d[0]:
w[0] -= x[2]
w[1] = w[1]
w[2] += x[2]
print(w)
print(w4)