拉格朗日函数、拉格朗日对偶问题、KKT条件个人理解
最近学习SVM的相关内容时,接触到了拉格朗日函数及其对偶问题,于是就学习了一些相关内容,在此整理总结一下。文章内容为个人理解,如有错误,欢迎指正!
文章目录
-
- 1. 引言
-
- 1.1 在约束条件下求函数的极值
- 1.2 引入拉格朗日乘数法
- 2. 拉格朗日乘数法
-
- 2.1 拉格朗日乘数法简介
- 2.2 几何理解:拉格朗日函数与梯度的关系
-
- 2.2.1 几何理解
- 2.2.2 举例
- 2.3 松弛条件与紧致条件
- 3. 拉格朗日对偶问题
-
- 3.1 关于“凸”
-
- 3.1.1 凸集
- 3.1.2 凸函数
- 3.1.3 凸优化问题
- 3.2 拉格朗日对偶问题
-
- 3.2.1 原始问题转换
- 3.2.2 对偶问题
- 3.3 原问题与对偶问题的关系
-
- 3.3.1 原问题的解 ≥ \ge ≥对偶问题的解恒成立
- 3.3.2 直观理解二者关系
- 3.3.3 原问题何时等价于其对偶问题
- 4. slater条件与KKT条件
-
- 4.1 slater条件
- 4.2 KKT条件
1. 引言
1.1 在约束条件下求函数的极值
我们一般见到的问题大多都是直接求函数的极值,通常我们会求解函数的导数并令其等于0来求出其极值。但是对于有约束条件的求函数极值的问题该怎么处理?
举例:求解
m i n f ( x , y ) = x 2 + y 2 s . t . x 2 + y = 0 min \ f(x,y)=x^2+y^2 \\ s.t. \ \ x^2 + y = 0 min f(x,y)=x2+y2s.t. x2+y=0
对于这个问题我们最先想到的就是将 y y y表示为 x x x的表达式,再带入到原函数中,之后通过对 x x x求导,得到可能的极值点,然后带入极值点求出最值。
但是,该方法存在局限性,倘若约束条件不存在代数解(即 y y y无法表示为 x x x的表达式),或者当无约束的目标函数表达式过于复杂,这时候该如何处理问题?
1.2 引入拉格朗日乘数法
拉格朗日乘数法(百度解释:链接)提供了一种方法:将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题,其变量不受任何约束。所以利用拉格朗日乘数法我们可以将原始的有约束条件的最优化问题,转变为没有约束条件的最优化问题。
2. 拉格朗日乘数法
2.1 拉格朗日乘数法简介
对于这样的问题:
m i n f ( x ) , x ∈ R n s . t . g i ( x ) ≤ 0 , i = 1 , 2 , 3 , . . . , m min\ f(\mathbf x),\ \mathbf x\in \mathbb R^n \\ s.t. \ \ g_i(\mathbf x)\le 0, i = 1,2,3,...,m min f(x), x∈Rns.t. gi(x)≤0,i=1,2,3,...,m
对于有多个约束条件的求极值/最值问题,可以构造拉格朗日函数:
L ( x , λ ) = f ( x ) + ∑ λ i g i ( x ) L(\mathbf x,\lambda)=f(\mathbf x)+\sum \lambda_i g_i(\mathbf x) L(x,λ)=f(x)+∑λigi(x)
并计算函数对每个变量的一阶偏导数并令其等于0,计算所得的解就是最优解的必要条件。
2.2 几何理解:拉格朗日函数与梯度的关系
其实,让拉格朗日函数梯度为0的点,就是可能的极值点,下面就理解一下拉格朗日函数与梯度的关系。
2.2.1 几何理解
假设现有问题,通过计算出可能的极值点,然后代入函数得到最小值:
m i n z = f ( x , y ) s . t . g ( x , y ) = 0 min \ \ z=f(x,y) \\ s.t. \ \ g(x,y)=0 min z=f(x,y)s.t. g(x,y)=0
注:图片来自https://zhuanlan.zhihu.com/p/103976631

我们从Z轴的方向俯瞰函数,图中的线就是函数的等值线。
把函数 z = f ( x , y ) z=f(x,y) z=f(x,y)想象成一个盆地, g ( x , y ) = 0 g(x,y)=0 g(x,y)=0想象成一个垂直于 x O y xOy xOy平面的一个曲面,这个曲面截出来的就是在约束条件 g ( x , y ) = 0 g(x,y)=0 g(x,y)=0下的函数 z = f ( x , y ) z=f(x,y) z=f(x,y),我们知道截出来的是一条曲线,假设这条曲线叫做 ϕ \phi ϕ。
假设点 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0)是曲线 ϕ \phi ϕ上的极值点,那么 P P P应该满足哪些条件?。从图中我们可以看到 P P P点处,曲线 g ( x , y ) = 0 g(x,y)=0 g(x,y)=0与 P P P处的等高线 z 1 = f ( x , y ) z_1=f(x,y) z1=f(x,y)相切,也就是说,这时候 P P P点处曲线 z 1 z_1 z1的法向量与曲线 g ( x , y ) = 0 g(x,y)=0 g(x,y)=0的法向量共线。
等高线 z 1 = f ( x , y ) z_1=f(x,y) z1=f(x,y)在 P P P处的法向量与函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在 P P P处的梯度共线(关于法向量和梯度的关系可参考:法向量,梯度)。因此在 P P P点处,函数 z = f ( x , y ) z=f(x,y) z=f(x,y)的梯度 ∇ p = { f x ′ ( x 0 , y 0 ) , f y ′ ( x 0 , y 0 ) } \nabla_p=\{ f_x^{'}(x_0,y_0), f_y^{'}(x_0,y_0) \} ∇p={fx′(x0,y0),fy′(x0,y0)}与曲线 g ( x , y ) = 0 g(x,y)=0 g(x,y)=0的法向量 { g x ′ ( x 0 , y 0 ) , g y ′ ( x 0 , y 0 ) } \{ g_x^{'}(x_0,y_0), g_y^{'}(x_0,y_0) \} {gx′(x0,y0),gy′(x0,y0)}共线。
由此我们可知 ∃ λ ∈ R \exists \lambda \in \mathbb R ∃λ∈R使得:
{ f x ′ ( x 0 , y 0 ) , f y ′ ( x 0 , y 0 ) } + λ { g x ′ ( x 0 , y 0 ) , g y ′ ( x 0 , y 0 ) } = 0 \{f_x^{'}(x_0,y_0), f_y^{'}(x_0,y_0) \} + \lambda \{ g_x^{'}(x_0,y_0), g_y^{'}(x_0,y_0) \} = 0 {fx′(x0,y0),fy′(x0,y0)}+λ{gx′(x0,y0),gy′(x0,y0)}=0
又 ∵ g ( x , y ) = 0 \because g(x,y)=0 ∵g(x,y)=0,将这些条件整合得到:
{ f x ′ = λ g x ′ f y ′ = λ g y ′ g ( x , y ) = 0 \begin{cases} f_x^{'} = \lambda g_x^{'} \\ f_y^{'} = \lambda g_y^{'}\\ g(x,y)=0 \end{cases} ⎩⎪⎨⎪⎧fx′=λgx′fy′=λgy′g(x,y)=0
然后我们求解这个方程组,就能得到条件极值点了。
采用拉格朗日乘数法,我们构造拉格朗日函数:
L ( x , y ) = f ( x , y ) + λ g ( x , y ) L(x,y)= f(x,y) + \lambda g(x,y) L(x,y)=f(x,y)+λg(x,y)
之后求解拉格朗日函数对每个变量的一阶偏导数并令其等于0,我们得到的方程组其实就是上文中推导出的方程组,只不过这里的 λ \lambda λ相当于上文方程组中的 − λ -\lambda −λ,但 λ \lambda λ本身就是个参数,它的作用就是用来调节两个向量的大小从而使得它们相加后为0:
{ ∂ L ( x , y ) ∂ x = ∂ f ( x , y ) ∂ x + λ ∂ g ( x , y ) ∂ x = 0 ∂ L ( x , y ) ∂ y = ∂ f ( x , y ) ∂ y + λ ∂ g ( x , y ) ∂ y = 0 ∂ L ( x , y ) ∂ λ = g ( x , y ) = 0 \begin{cases} \cfrac{\partial L(x,y)}{\partial x} = \cfrac{\partial f(x,y)}{\partial x} + \lambda \cfrac{\partial g(x,y)}{\partial x} = 0\\ \cfrac{\partial L(x,y)}{\partial y} = \cfrac{\partial f(x,y)}{\partial y} + \lambda \cfrac{\partial g(x,y)}{\partial y} = 0\\ \cfrac{\partial L(x,y)}{\partial \lambda} = g(x,y) =0 \end{cases} ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧∂x∂L(x,y)=∂x∂f(x,y)+λ∂x∂g(x,y)=0∂y∂L(x,y)=∂y∂f(x,y)+λ∂y∂g(x,y)=0∂λ∂L(x,y)=g(x,y)=0
2.2.2 举例
-
示例函数
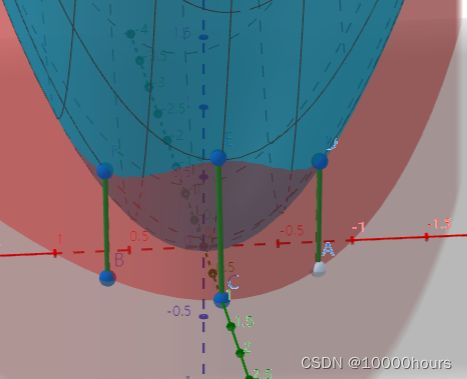
为了更好地理解,这里举个例子:假设函数 z = f ( x , y ) = x 2 + y 2 z=f(x,y)=x^2+y^2 z=f(x,y)=x2+y2, g ( x , y ) = x 2 + y − 1 = 0 g(x,y)=x^2+y-1=0 g(x,y)=x2+y−1=0,分别从z,y,x轴来看,分别如下图的图(a)(b)(c)所示,假设 f ( x , y ) f(x,y) f(x,y)被 g ( x , y ) = 0 g(x,y)=0 g(x,y)=0截出来的曲线为 ϕ \phi ϕ :

(a) 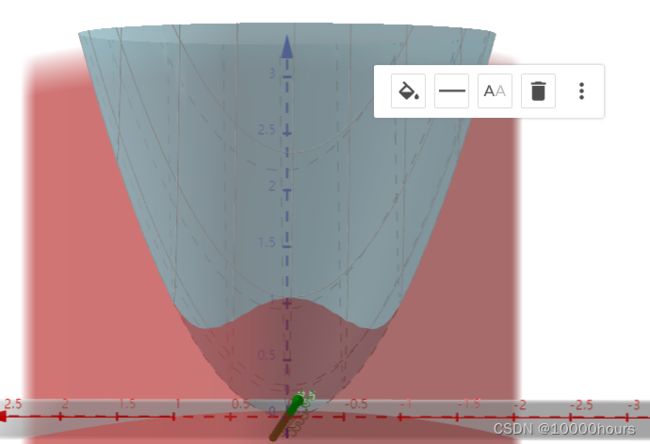
(b) 
(c) 通过观察图(b)可以很容易发现曲线 ϕ \phi ϕ有两个极小点和一个极大值点。在图中标出这三个点,并得到这三个点在 x O y xOy xOy平面上的投影点 A ( − 2 2 , 1 2 ) , B ( 2 2 , 1 2 ) , C ( 0 , 1 ) A(-\cfrac{\sqrt{2}}{2},\cfrac{1}{2}),B(\cfrac{\sqrt{2}}{2},\cfrac{1}{2}),C(0,1) A(−22,21),B(22,21),C(0,1)
-
拉格朗日乘数法的应用
接着用拉格朗日乘数法来求解 A , B , C A,B,C A,B,C点的坐标。- 构造拉格朗日函数
L ( x , y , λ ) = x 2 + y 2 + λ ( x 2 + y − 1 ) L(x,y,\lambda) = x^2+y^2 + \lambda(x^2+y-1) L(x,y,λ)=x2+y2+λ(x2+y−1) - 令拉格朗日函数的梯度为0
{ ∂ L ∂ x = 2 x + 2 λ x = 0 ∂ L ∂ y = 2 y + λ = 0 ∂ L ∂ λ = x 2 + y − 1 = 0 ⇒ { x ( 1 + λ ) = 0 y = − λ 2 x 2 + y − 1 = 0 \begin{cases} \cfrac{\partial L}{\partial x} = 2x+2\lambda x = 0 \\ \cfrac{\partial L}{\partial y} = 2y + \lambda = 0 \\ \cfrac{\partial L}{\partial \lambda} = x^2+y-1 = 0 \end{cases} \ \ \ \ \ \ \ \Rightarrow \begin{cases} x(1+\lambda)= 0 \\ y = -\cfrac{\lambda}{2}\\ x^2+y-1=0 \end{cases} ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧∂x∂L=2x+2λx=0∂y∂L=2y+λ=0∂λ∂L=x2+y−1=0 ⇒⎩⎪⎪⎨⎪⎪⎧x(1+λ)=0y=−2λx2+y−1=0 - 求出极值点
1 o 1^o 1o : 若 x ≠ 0 x\neq 0 x=0,则 λ = − 1 , ⇒ y = 1 2 \lambda = -1, \Rightarrow y=\cfrac{1}{2} λ=−1,⇒y=21,带入 x 2 + y − 1 = 0 x^2+y-1=0 x2+y−1=0 得 x = ± 2 2 x= \pm \cfrac{\sqrt 2}{2} x=±22。得到极值点 ( − 2 2 , 1 2 ) , ( 2 2 , 1 2 ) (-\cfrac{\sqrt 2}{2}, \cfrac{1}{2}),(\cfrac{\sqrt 2}{2}, \cfrac{1}{2}) (−22,21),(22,21)。
2 o 2^o 2o : 若 y ≠ 0 y\neq 0 y=0,则 λ ≠ 0 \lambda \neq 0 λ=0(且 λ ≠ − 1 \lambda \neq -1 λ=−1) ⇒ x = 0 \Rightarrow x=0 ⇒x=0,带入 x 2 + y − 1 = 0 x^2+y-1=0 x2+y−1=0 得 y = 1 , λ = − 2 y=1,\lambda = -2 y=1,λ=−2。得到极值点 ( 0 , 1 ) (0,1) (0,1)。
在上文中提到了极值点处, g ( x , y ) = 0 g(x,y)=0 g(x,y)=0应该与 f ( x , y ) f(x,y) f(x,y)对应的等高线相切,那么我们从图中直观的看一下。俯瞰函数,图中紫色线 l 1 l_1 l1是 f ( x , y ) f(x,y) f(x,y)在 C C C处的等高线,蓝色线 l 2 l_2 l2是 f ( x , y ) f(x,y) f(x,y)在 A , B A,B A,B处的等高线,绿色线 l 3 l_3 l3是 g ( x , y ) = 0 g(x,y)=0 g(x,y)=0在 x O y xOy xOy平面的投影。我们可以很容易看出: l 3 l_3 l3与 l 1 , l 2 l_1, l_2 l1,l2分别相切于点 C , A , B C,A,B C,A,B:
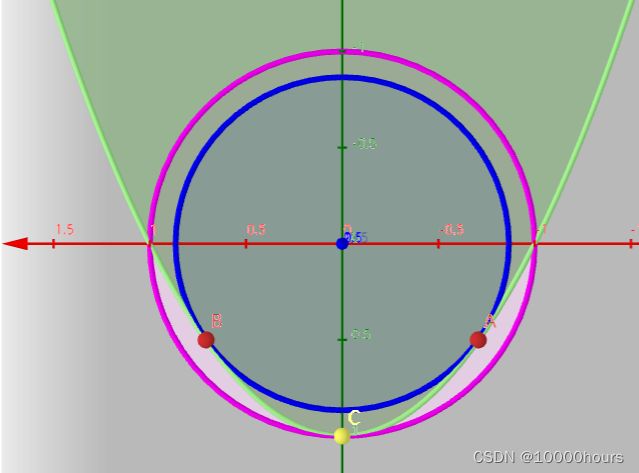
- 构造拉格朗日函数
2.3 松弛条件与紧致条件
当约束条件有多个时,所有的约束条件都一定会起作用吗?来看这样的问题:
m i n f ( x ) , x ∈ R n s . t . g i ( x ) = ω i T ⋅ x + b i ≤ 0 i = 1 , 2 , … , m , ω i ∈ R n , b i ∈ R min \ \ f(x), x \in \mathbb R^n \\ s.t. \ \ g_i(x) = \omega_i^T \cdot x + b_i \le 0\\ i = 1,2,\dots ,m, \omega_i \in \mathbb R^n, b_i \in \mathbb R min f(x),x∈Rns.t. gi(x)=ωiT⋅x+bi≤0i=1,2,…,m,ωi∈Rn,bi∈R
构建拉格朗日函数:
L ( x , λ ) = f ( x ) + ∑ i = 1 m λ i g i ( x ) L(x, \lambda) = f(x) + \sum_{i=1}^m\lambda_i g_i(x) L(x,λ)=f(x)+i=1∑mλigi(x)
假设由5个约束条件得到的可行域是这样的:
注:图片截自https://www.bilibili.com/video/BV1HP4y1Y79e?spm_id_from=333.880.my_history.page.click
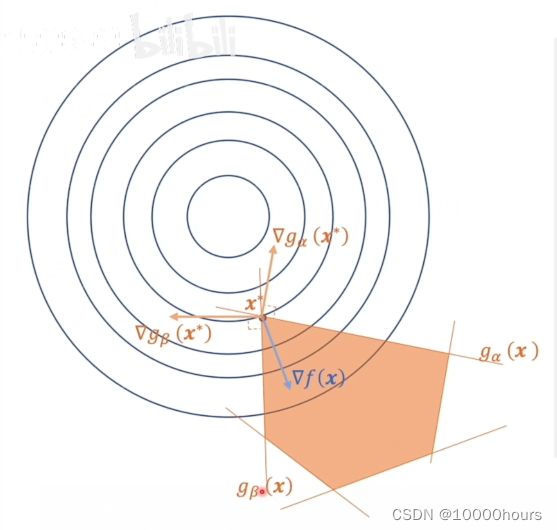
根据2.2的经验,我们知道可能的极值点应该是 x ∗ x^* x∗。我们令函数的梯度等于0,得到:
∇ L ( x , λ ) = 0 ⇒ − ∇ f ( x ) = ∑ i = 1 m λ i ⋅ ∇ g i ( x ) \nabla L(x,\lambda) = 0 \Rightarrow -\nabla f(x) = \sum_{i=1}^m\lambda_i \cdot \nabla g_i(x) ∇L(x,λ)=0⇒−∇f(x)=i=1∑mλi⋅∇gi(x)
由此可知 ∇ f \nabla f ∇f 的反方向,就等于所有约束条件的梯度和(注意梯度是个向量),但是我们观察图2发现,真正起作用的梯度只有 ∇ g α ( x ∗ ) \nabla g_{\alpha}(x^*) ∇gα(x∗) 和 ∇ g β ( x ∗ ) \nabla g_{\beta}(x^*) ∇gβ(x∗),也就是说:
λ α ∇ g α ( x ∗ ) + λ β ∇ g β ( x ∗ ) = − ∇ f ( x ) ⇒ λ α , λ β ≠ 0 \lambda_{\alpha} \nabla g_{\alpha}(x^*) + \lambda_{\beta} \nabla g_{\beta}(x^*) = -\nabla f(x) \ \ \ \ \Rightarrow \ \ \ \ \ \lambda_{\alpha}, \lambda_{\beta} \neq 0 λα∇gα(x∗)+λβ∇gβ(x∗)=−∇f(x) ⇒ λα,λβ=0
我们可以看到 x ∗ x^* x∗落在约束条件 g α g_{\alpha} gα和 g β g_{\beta} gβ上,也就是说:
g α ( x ∗ ) = 0 , g β ( x ∗ ) = 0 g_{\alpha}(x^*)=0, \ \ \ \ g_{\beta}(x^*) = 0 gα(x∗)=0, gβ(x∗)=0
将 x ∗ x^* x∗带入待其他约束条件中,可以发现其他的 g i ( x ∗ ) < 0 g_i(x^*) \lt 0 gi(x∗)<0。那么为了让其他的 ∇ g i ( x ∗ ) \nabla g_i(x^*) ∇gi(x∗)不起作用,我们需要通过调整 λ i \lambda_i λi的值,使得
λ i ⋅ ∇ g i ( x ∗ ) = 0 ⇒ λ i = 0 , 其 中 i ≠ α , β \lambda_i \cdot \nabla g_i(x^*)=0 \ \ \ \ \Rightarrow \ \ \ \ \lambda_i = 0,其中i\neq \alpha ,\beta λi⋅∇gi(x∗)=0 ⇒ λi=0,其中i=α,β
直观的看

那么对于 λ i \lambda_i λi( λ i ≥ 0 \lambda_i \ge 0 λi≥0,关于拉格朗日乘子 ≥ 0 \ge 0 ≥0可参考链接)就有如下结论:
(1)若 λ i = 0 \lambda_i =0 λi=0,就说对应的约束条件 g i ( x ) g_i(x) gi(x)是松弛的;
(2)若 λ i > 0 \lambda_i \gt 0 λi>0,就说对应的约束条件 g i ( x ) g_i(x) gi(x)是紧致的。
3. 拉格朗日对偶问题
当我们求函数的最值时,先使用拉格朗日乘数法找出的可能的点(这些点可能是极值点,也可能是鞍点),所以说我们还需要对找出的点做进一步的筛选,来确定最终的最值。那么什么时候函数的极值就是最值呢?思考中学学过的凸函数,当一个函数是凸函数时,该函数的极值就是最值。同样的,当我们的优化问题是一个凸问题时,求解的极值就是最值。
3.1 关于“凸”
在了解拉格朗日对偶问题之前,先了解一下几个和“凸”有关的概念。
3.1.1 凸集
凸集:百度百科。用白话来讲,用二维平面几何图形举例,凸集就是图形中任意两个点连成的线段也在这个图形中,也就是如下图所示:

3.1.2 凸函数
关于凹凸函数的定义,国内有些数学界的定义和国外数学界的定义是相反的,但是不管怎么定义,凸函数取反就是凹函数,反之亦然。按照百度百科对凸函数的定义:凸函数是一个定义在某个向量空间的凸子集 C C C上的实值函数 f f f,而且对于凸子集 C C C中任意两个向量 x 1 , x 2 \mathbf x_1, \mathbf x_2 x1,x2 有 f ( x 1 + x 2 2 ) ≤ f ( x 1 ) + f ( x 2 ) 2 f(\cfrac{\mathbf x_1+ \mathbf x_2}{2}) \le \cfrac{f(\mathbf x_1) + f(\mathbf x_2)}{2} f(2x1+x2)≤2f(x1)+f(x2)成立。可以把它想象成一个开口朝下的二次函数。
3.1.3 凸优化问题
凸优化问题是研究定义于凸集中的凸函数最小化的问题。也就是说问题的定义域是个凸集,问题对应的函数是个凸函数。
3.2 拉格朗日对偶问题
假设现有这样的问题:
m i n f ( x ) , x ∈ R n s . t . g i ( x ) ≤ 0 i = 1 , 2 , . . . , m h j ( x ) = 0 j = 1 , 2 , . . . , n min \ \ f(x) , x \in \mathbb R^n\\ s.t. \ \ g_i(x) \le 0 \ \ i = 1,2,...,m\\ \ \ \ \ \ \ h_j(x) = 0 \ \ j = 1,2,...,n min f(x),x∈Rns.t. gi(x)≤0 i=1,2,...,m hj(x)=0 j=1,2,...,n
3.2.1 原始问题转换
利用拉格朗日乘数法,我们可以构造拉格朗日函数:
L ( x , λ , μ ) = f ( x ) + ∑ i = 1 m λ i g i ( x ) + ∑ j = 1 n μ j h j ( x ) L(x, \lambda, \mu) = f(x) + \sum_{i=1}^m \lambda_i g_i(x) + \sum_{j=1}^n \mu_j h_j(x) L(x,λ,μ)=f(x)+i=1∑mλigi(x)+j=1∑nμjhj(x)
之后要做的就是 m i n L ( x , λ , μ ) min \ \ L(x,\lambda, \mu) min L(x,λ,μ),但是拉格朗日函数有三个变量,如何对其进行最小化?其实是分两步进行的:
(1)先将 x x x看做常量,对 λ , μ \lambda, \mu λ,μ求最大值;
(2)确定了 λ , μ \lambda, \mu λ,μ之后,对 x x x求最小值.
于是就将原始的问题转化成了:
min x max λ , μ L ( x , λ , μ ) s . t . λ ≥ 0 \min_{x}\max_{\lambda, \mu} L(x,\lambda, \mu)\\ s.t. \ \ \lambda \ge 0 xminλ,μmaxL(x,λ,μ)s.t. λ≥0
为什么要这样转换呢?我们先来分析一下原始问题:原始问题是有约束条件的最小化问题,也就是说在全局范围内, x x x要么在可行域(即满足约束条件)内,要么在可行域之外,那就分两种情况讨论:
-
x x x在可行域内
此时 x x x满足所有的约束条件,即 g i ( x ) ≤ 0 i = 1 , 2 , . . . , m h j ( x ) = 0 j = 1 , 2 , . . . , n g_i(x) \le 0 \ \ i = 1,2,...,m \ \ \ h_j(x) = 0 \ \ j= 1,2,...,n gi(x)≤0 i=1,2,...,m hj(x)=0 j=1,2,...,n。
∵ h j ( x ) = 0 \because h_j(x)=0 ∵hj(x)=0, ∴ \therefore ∴无论 μ j \mu_j μj取什么值,一定有 μ j h j ( x ) = 0 \mu_jh_j(x)=0 μjhj(x)=0。
又 ∵ g i ( x ) ≤ 0 \because g_i(x) \le 0 ∵gi(x)≤0,且 λ i ≥ 0 \lambda_i \ge 0 λi≥0, ∴ λ i g i ( x ) \therefore \lambda_ig_i(x) ∴λigi(x)的最大值为0.
因此,在可行域内有:
max λ i , μ j ; λ i ≥ 0 L ( x , λ , μ ) = f ( x ) + max λ i , μ j ; λ i ≥ 0 [ ∑ i = 1 m λ i g i ( x ) + ∑ j = 1 n μ j h j ( x ) ] = f ( x ) \max_{\lambda_i, \mu_j;\lambda_i \ge 0} L(x, \lambda, \mu) = f(x) + \max_{\lambda_i, \mu_j;\lambda_i \ge 0}[\sum_{i=1}^m \lambda_i g_i(x) + \sum_{j=1}^n \mu_j h_j(x)] = f(x) λi,μj;λi≥0maxL(x,λ,μ)=f(x)+λi,μj;λi≥0max[i=1∑mλigi(x)+j=1∑nμjhj(x)]=f(x) -
x x x在可行域外
此时 x x x不满足所有的约束条件。若 h j ( x ) ≠ 0 h_j(x) \neq 0 hj(x)=0,那么最大化之后 μ j h j ( x ) → + ∞ \mu_jh_j(x) \rightarrow + \infty μjhj(x)→+∞。若 g i ( x ) > 0 g_i(x) \gt 0 gi(x)>0,那么最大化之后 λ i g i ( x ) → + ∞ \lambda_ig_i(x) \rightarrow +\infty λigi(x)→+∞。
因此,在可行域之外有:
max λ i , μ j ; λ i ≥ 0 L ( x , λ , μ ) = + ∞ \max_{\lambda_i, \mu_j;\lambda_i \ge 0} L(x, \lambda, \mu) =+\infty λi,μj;λi≥0maxL(x,λ,μ)=+∞
综合1、 2可知,对 f ( x ) f(x) f(x)在可行域内进行最小化时,就相当于最小化 max λ i , μ j ; λ i ≥ 0 L ( x , λ , μ ) \max_{\lambda_i, \mu_j;\lambda_i \ge 0} L(x, \lambda, \mu) maxλi,μj;λi≥0L(x,λ,μ);在可行域之外, max λ i , μ j ; λ i ≥ 0 L ( x , λ , μ ) \max_{\lambda_i, \mu_j;\lambda_i \ge 0} L(x, \lambda, \mu) maxλi,μj;λi≥0L(x,λ,μ)趋向于正无穷大,没有极值。
综合来说就是 min x { f ( x ) , + ∞ } \min_x\{f(x), +\infty\} minx{f(x),+∞}。因此,当我们尝试最小化 max λ i , μ j ; λ i ≥ 0 L ( x , λ , μ ) \max_{\lambda_i, \mu_j;\lambda_i \ge 0} L(x, \lambda, \mu) maxλi,μj;λi≥0L(x,λ,μ)时,就相当于求解原始问题:在约束条件下最小化 f ( x ) f(x) f(x)。
到这儿我们就知道了使用拉格朗日乘数法构造拉格朗日函数后,为什么要先最大化然后再最小化。那么我们称转换后的问题为原问题,即:
min x max λ , μ L ( x , λ , μ ) s . t . λ ≥ 0 \min_{x}\max_{\lambda, \mu} L(x,\lambda, \mu)\\ s.t. \ \ \lambda \ge 0 xminλ,μmaxL(x,λ,μ)s.t. λ≥0
参考:拉格朗日函数为什么要先最大化?
3.2.2 对偶问题
对于任何一个拉格朗日函数,它都有与其对应的对偶函数,该对偶函数的自变量含有拉格朗日乘子。对于我们在3.2.1中构造的拉格朗日函数,我们可以构造它的对偶函数:
φ ( λ , μ ) = min x L ( x , λ , μ ) \varphi (\lambda,\mu) = \min_x L(x, \lambda, \mu) φ(λ,μ)=xminL(x,λ,μ)
那么原问题(参见3.2.1末尾)的对偶问题就是:
max λ , μ φ ( λ , μ ) = max λ , μ min x L ( x , λ , μ ) s . t . λ ≥ 0 \max_{\lambda, \mu} \varphi (\lambda, \mu)= \max_{\lambda, \mu} \min_x L(x, \lambda, \mu)\\ s.t. \ \ \lambda \ge 0 λ,μmaxφ(λ,μ)=λ,μmaxxminL(x,λ,μ)s.t. λ≥0
看起来就是原问题的计算顺序反过来了:先求最小再求最大。其实这个对 x x x求最小 min x L ( x , λ , μ ) \min_x L(x, \lambda, \mu) minxL(x,λ,μ)其实就相当于函数对 x x x的梯度为0,所以可以将对偶问题等价表示为:
max λ , μ φ ( λ , μ ) s . t . ∇ x L ( x , λ , μ ) = 0 λ ≥ 0 \max_{\lambda, \mu} \varphi (\lambda, \mu) \\ s.t. \ \ \nabla_x L(x, \lambda, \mu) = 0 \\ \lambda \ge 0 λ,μmaxφ(λ,μ)s.t. ∇xL(x,λ,μ)=0λ≥0
在这里还要说明一条重要的结论:对偶问题一定是凸优化问题。 对于上文中提到的对偶函数 φ ( λ , μ ) = min x L ( x , λ , μ ) \varphi(\lambda,\mu)=\min_x L(x,\lambda,\mu) φ(λ,μ)=minxL(x,λ,μ),假设我们现在求得了使函数 L L L最小的 x ∗ x^* x∗,那么对偶函数就可以表示为:
φ ( λ , μ ) = f ( x ∗ ) + ∑ i = 1 m λ i g i ( x ∗ ) + ∑ j = 1 n μ j h j ( x ∗ ) \varphi(\lambda, \mu) = f(x^*) + \sum_{i=1}^m\lambda_ig_i(x^*) +\sum_{j=1}^n\mu_jh_j(x^*) φ(λ,μ)=f(x∗)+i=1∑mλigi(x∗)+j=1∑nμjhj(x∗)
其中 f ( x ∗ ) , g i ( x ∗ ) , h j ( x ∗ ) f(x^*), \ g_i(x^*), \ h_j(x^*) f(x∗), gi(x∗), hj(x∗)都是常量,也就是说 φ ( λ , μ ) \varphi(\lambda, \mu) φ(λ,μ)是一条在 λ , μ \lambda,\mu λ,μ构成的平面上的直线,根据凸函数和凹函数的定义我们知道直线既是凸函数也是凹函数,而且约束条件 λ ≥ 0 \lambda \ge 0 λ≥0是个凸集。对偶问题是求函数 φ ( λ , μ ) \varphi(\lambda, \mu) φ(λ,μ)的最大值,那么我们将函数反过来取个负号问题不就变成了最小化的问题了吗,而且函数反过来它照样是个凸函数。
综上所述,对偶问题满足:(1)问题的定义域是个凸集;(2)问题对应的函数是个凸函数;(3)求解的是函数最小化问题。因此对偶问题满足凸优化问题的所有条件(参见3.1.3凸优化问题),所以对偶问题是凸优化问题。
- 说明:详细证明请自主查阅资料,这里仅简单举例说明。
- 补充:拉格朗日对偶函数的一个重要性质是,不论原问题是否为凸问题,拉格朗日对偶函数一定是个凹函数。
3.3 原问题与对偶问题的关系
经过上述讨论我们知道对偶问题一定是个凸优化问题,既然对偶问题有这么好的性质,那是不是所有的问题都可以通过求解其对偶问题,来得到最优解呢?No,no,no.接下来我们讨论一下原问题与其对偶问题的关系。
3.3.1 原问题的解 ≥ \ge ≥对偶问题的解恒成立
先把原问题与对偶问题摆出来:
原 问 题 : min x max λ , μ L ( x , λ , μ ) 对 偶 问 题 : max λ , μ min x L ( x , λ , μ ) s . t . λ ≥ 0 s . t . λ ≥ 0 原问题:\min_x\max_{\lambda,\mu}L(x,\lambda,\mu) \ \ \ \ \ \ \ \ \ \ \ \ \ 对偶问题:\max_{\lambda, \mu}\min_x L(x,\lambda,\mu)\\ s.t.\ \ \lambda \ge 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ s.t. \lambda \ge 0 原问题:xminλ,μmaxL(x,λ,μ) 对偶问题:λ,μmaxxminL(x,λ,μ)s.t. λ≥0 s.t.λ≥0
来看如下推导过程:
max λ , μ L ( x , λ , μ ) ≥ L ( x , λ , μ ) ≥ min x L ( x , λ , μ ) ⇓ max λ , μ L ( x , λ , μ ) ≥ min x max λ , μ L ( x , λ , μ ) ≥ max λ , μ min x L ( x , λ , μ ) ≥ min x L ( x , λ , μ ) ⇓ P ∗ = min x max λ , μ L ( x , λ , μ ) ≥ max λ , μ min x L ( x , λ , μ ) = D ∗ \max_{\lambda, \mu} L(x,\lambda,\mu) \ge L(x,\lambda,\mu) \ge \min_x L(x,\lambda,\mu) \\ \Downarrow\\ \max_{\lambda, \mu} L(x,\lambda,\mu) \ge \min_x \max_{\lambda, \mu} L(x,\lambda,\mu) \ge \max_{\lambda,\mu}\min_x L(x,\lambda,\mu) \ge \min_x L(x,\lambda,\mu)\\ \Downarrow\\ P^* = \min_x \max_{\lambda, \mu} L(x,\lambda,\mu) \ge \max_{\lambda,\mu}\min_x L(x,\lambda,\mu)=D^* λ,μmaxL(x,λ,μ)≥L(x,λ,μ)≥xminL(x,λ,μ)⇓λ,μmaxL(x,λ,μ)≥xminλ,μmaxL(x,λ,μ)≥λ,μmaxxminL(x,λ,μ)≥xminL(x,λ,μ)⇓P∗=xminλ,μmaxL(x,λ,μ)≥λ,μmaxxminL(x,λ,μ)=D∗
我们将 P ∗ P^* P∗称为原问题的解, D ∗ D^* D∗称为对偶问题的解,可知 P ∗ ≥ D ∗ P^* \ge D^* P∗≥D∗恒成立,也就是说原问题的解恒大于等于对偶问题的解。
3.3.2 直观理解二者关系
∙ \bullet ∙ 变换表示形式
我们先前构造的拉格朗日函数是 L ( x , λ , μ ) = f ( x ) + ∑ i = 1 m λ i g i ( x ) + ∑ j = 1 n μ j h j ( x ) L(x, \lambda, \mu) = f(x) + \sum_{i=1}^m \lambda_i g_i(x) + \sum_{j=1}^n \mu_j h_j(x) L(x,λ,μ)=f(x)+∑i=1mλigi(x)+∑j=1nμjhj(x),由于原始问题中的约束条件 h j ( x ) = 0 h_j(x)=0 hj(x)=0,因此这里我们将拉格朗日函数简化一下表示为 L ( x , λ , μ ) = f ( x ) + ∑ i = 1 m λ i g i ( x ) L(x, \lambda, \mu) = f(x) + \sum_{i=1}^m \lambda_i g_i(x) L(x,λ,μ)=f(x)+∑i=1mλigi(x),进一步简化,用向量来表示:
L ( x , λ , μ ) = t + λ T ⋅ u 其 中 t = f ( x ) , u = ∑ i = 1 m λ i g i ( x ) 均 为 向 量 L(x, \lambda, \mu) = \mathbf{ t + \lambda^T \cdot u} \ \ \ \ 其中\mathbf{t=f(\mathbf x),u=\sum_{i=1}^m \lambda_i g_i(x)}均为向量 L(x,λ,μ)=t+λT⋅u 其中t=f(x),u=i=1∑mλigi(x)均为向量
之后我们重新表示一下原问题与对偶问题:
G 1 = { ( t , u ) ∣ t = f ( x ) , u i = g i ( x ) , x ∈ D } D = { x ∣ g i ( x ) ≤ 0 i = 1 , 2 , . . . , m h j ( x ) = 0 j = 1 , 2 , . . . , n } ⇓ 原 问 题 : min x { t ∣ ( t , u ) ∈ G 1 , u ≤ 0 } G_1 = \{ (\mathbf {t,u}) | t=f(\mathbf x), \mathbf{u_i = g_i(x), \mathbf{x \in D}}\} \\ D = \{\mathbf{x | g_i(x) \le 0 \ \ i = 1,2,...,m \ \ \ h_j(x) = 0 \ \ j= 1,2,...,n}\}\\ \Downarrow \\ 原问题:\min_x \{ \mathbf{t | (t,u) \in G_1, u\le 0}\} G1={(t,u)∣t=f(x),ui=gi(x),x∈D}D={x∣gi(x)≤0 i=1,2,...,m hj(x)=0 j=1,2,...,n}⇓原问题:xmin{t∣(t,u)∈G1,u≤0}
G 2 = { ( t , u ) ∣ t = f ( x ) , u i = g i ( x ) , x ∈ R n } ⇓ 对 偶 问 题 : max λ min x { t + λ T ⋅ u ∣ ( t , u ) ∈ G 2 , λ ≥ 0 } G_2 = \{ \mathbf{(t,u)|t=f(x), u_i = g_i(x), x \in \mathbb R^n}\} \\ \Downarrow\\ 对偶问题:\max_{\lambda}\min_x\{ \mathbf{t + \lambda^T \cdot u | (t,u) \in G_2, \lambda \ge 0}\} G2={(t,u)∣t=f(x),ui=gi(x),x∈Rn}⇓对偶问题:λmaxxmin{t+λT⋅u∣(t,u)∈G2,λ≥0}
∙ \bullet ∙ 可视化
接着来降维理解一下,我们把 t , u \mathbf{t,u} t,u想象成二维平面上的变量,之后通过二维平面图形来理解一下原问题与对偶问题的关系。
原 问 题 : min x { t ∣ ( t , u ) ∈ G 1 , u ≤ 0 } 对 偶 问 题 : max λ min x { t + λ T ⋅ u ∣ ( t , u ) ∈ G 2 , λ ≥ 0 } 原问题:\min_x \{ \mathbf{t | (t,u) \in G_1,u \le 0 }\} \ \ \ \ 对偶问题:\max_{\lambda}\min_x\{ \mathbf{t + \lambda^T \cdot u | (t,u) \in G_2, \lambda \ge 0}\} 原问题:xmin{t∣(t,u)∈G1,u≤0} 对偶问题:λmaxxmin{t+λT⋅u∣(t,u)∈G2,λ≥0}
注:图片截自https://www.bilibili.com/video/BV1HP4y1Y79e?spm_id_from=333.880.my_history.page.click
 |
 |
|---|
图中 G 1 G_1 G1为原问题的可行域, G 2 G_2 G2为对偶问题的可行域。
(1)对于原问题,要求解的是 G 1 G_1 G1范围内且 u ≤ 0 \mathbf u \le0 u≤0, t \mathbf t t的最小值,可以很容易找到对应的解就是图中的 P ∗ P^* P∗
(2)对于对偶问题,它要分为两步来看,第一步是min,第二步是max。首先我们将 t + λ T ⋅ u t+\lambda^T \cdot u t+λT⋅u看做一条直线, − λ T -\lambda^T −λT就相当于直线的斜率。(对应着看: y + k x = b y+kx=b y+kx=b)
-
min:在定义域内,首先在 λ ( λ ≥ 0 ) \lambda(\lambda \ge 0) λ(λ≥0)固定的情况下(就相当于直线的斜率固定),找到 t + λ T ⋅ u t+\lambda^T \cdot u t+λT⋅u的最小值。其实 t + λ T ⋅ u t+\lambda^T \cdot u t+λT⋅u就相当于直线在 t t t上的截距(对应着看: y + k x = b y+kx=b y+kx=b),所以也就是相当于在直线斜率固定的情况下平移直线,使得直线在 t t t轴上的截距最小,也就是左图中深绿色的线与 t t t的绿色交点。所以我们在定义域内确定了一点 A A A(如左图所示)。
-
max: 在第一步中确定了一点 A A A,接着需要变动直线的斜率 − λ T -\lambda^T −λT使得直线的截距最大,也就是在保证 λ ≥ 0 \lambda \ge 0 λ≥0的情况下,绕着 A A A旋转直线,使得直线在 t t t上的截距最大。最终得到了对偶函数的解 D ∗ D^* D∗。
从图中我们也能直观的看到原问题的解一定是大于等于对偶问题的解的。
3.3.3 原问题何时等价于其对偶问题
求解原问题时我们希望它和其对偶问题是等价的,这样直接求解对偶问题的解就相当与求解原问题,那么什么情况下原问题和对偶问题才能等价呢?首先介绍一下强弱对偶关系。
假设原问题的解是 P ∗ P^* P∗,对偶问题的解是 D ∗ D^* D∗:
∙ \bullet ∙ 强对偶关系 D ∗ = P ∗ D^* = P^* D∗=P∗
∙ \bullet ∙ 弱对偶关系 D ∗ ≤ P ∗ D^* \le P^* D∗≤P∗
所以说当问题满足强对偶关系时,原问题与其对偶问题是等价的,此时对偶问题的解就相当于原问题的解。
考虑上文中求解 P ∗ , D ∗ P^*,D^* P∗,D∗,如果可行域变成了一个凸集,那么此时就有 P ∗ = D ∗ P^*=D^* P∗=D∗:
注:图片截自https://www.bilibili.com/video/BV1HP4y1Y79e?spm_id_from=333.880.my_history.page.click
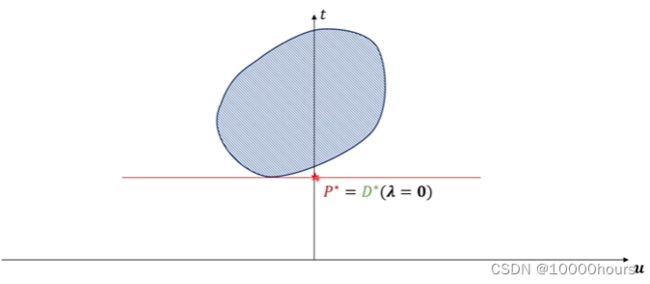
其实这就是一个凸优化问题,但是凸优化问题不一定满足强对偶关系,当凸优化问题满足slater条件时,则有强对偶关系。接下来就简单介绍一下slater条件。
4. slater条件与KKT条件
对于一个凸优化问题:
m i n f ( x ) , x ∈ R n s . t . g i ( x ) ≤ 0 i = 1 , 2 , . . . , m h j ( x ) = 0 j = 1 , 2 , . . . , n min \ \ f(x) , x \in \mathbb R^n\\ s.t. \ \ g_i(x) \le 0 \ \ i = 1,2,...,m\\ \ \ \ \ \ \ h_j(x) = 0 \ \ j = 1,2,...,n min f(x),x∈Rns.t. gi(x)≤0 i=1,2,...,m hj(x)=0 j=1,2,...,n
4.1 slater条件
∃ x ∈ r e l i n t D \exist x \in relint\ D ∃x∈relint D,使得 g i ( x ) < 0 , i = 1 , 2 , . . . , m g_i(x) \lt 0, i=1,2,...,m gi(x)<0,i=1,2,...,m,其中 r e l i n t D relint \ D relint D指的是定义域 D D D内部。
也就是说,若定义域内至少有一个点使得所有不等式约束条件都不取等号,就满足slater条件。
当原问题是凸问题且满足slater条件时,则该问题一定是强对偶 的。但是一个强对偶问题不一定满足slater条件。
4.2 KKT条件
KKT条件是强对偶问题的必要条件,即强对偶问题一定满足KKT条件。
对于上述的凸优化问题,我们构造拉格朗日函数如下:
L ( x , λ , μ ) = f ( x ) + ∑ i = 1 m λ i g i ( x ) + ∑ j = 1 n μ j h j ( x ) L(x, \lambda, \mu) = f(x) + \sum_{i=1}^m \lambda_i g_i(x) + \sum_{j=1}^n \mu_j h_j(x) L(x,λ,μ)=f(x)+i=1∑mλigi(x)+j=1∑nμjhj(x)
可知该问题的对偶问题为:
max λ , μ φ ( λ , μ ) , 其 中 φ ( λ , μ ) = min x L ( x , λ , μ ) s . t . ∇ x L ( x , λ , μ ) = 0 λ ≥ 0 \max_{\lambda, \mu} \varphi (\lambda, \mu),其中\varphi (\lambda, \mu)=\min_xL(x,\lambda,\mu) \\ s.t. \ \ \nabla_x L(x, \lambda, \mu) = 0 \\ \lambda \ge 0 λ,μmaxφ(λ,μ),其中φ(λ,μ)=xminL(x,λ,μ)s.t. ∇xL(x,λ,μ)=0λ≥0
∙ \bullet ∙ KKT条件
- 原问题可行条件
g i ( x ) ≤ 0 h i ( x ) = 0 g_i(x) \le 0\\ h_i(x) =0 gi(x)≤0hi(x)=0 - 对偶问题可行条件
∇ x L ( x , λ , μ ) = 0 λ ≥ 0 \nabla_x L(x,\lambda, \mu) = 0\\ \lambda \ge 0 ∇xL(x,λ,μ)=0λ≥0 - 互补松弛条件
λ i g i ( x ) = 0 \lambda_ig_i(x)=0 λigi(x)=0
这五个条件项共同组成了KKT条件。
∙ \bullet ∙ 说明
虽然KKT条件是强对偶问题的必要条件,但是一般在使用时,只要不是特别冷门偏僻的问题,我们是可以把KKT条件当做强对偶问题的充分必要条件使用的。
参考资料:
[1] B站: 拉格朗日乘数法
[2] B站:“拉格朗日对偶问题”如何直观理解?“KKT条件” “Slater条件” “凸优化”打包理解
[3] 周志华老师博客:Lagrange乘数法
[4] 知乎:条件极值,拉格朗日乘数法
[5] 简易解说拉格朗日对偶
[6] 拉格朗日对偶理解
[7] KKT条件