【NOIP模拟】 (10.26) T2 做运动
做运动
题目描述:(应出题人要求不传播)
解析:
最小生成树+并查集+dijkstra+优化
一道综合性较强的题,刚拿到题目时一看。最高的最低,二分??于是我就成功T了。。。。
后来考完后分析了一下,发现自己真是弱爆了。本来数据可就很大,用二分虽然比普通暴力扫好一些,但仍然至少要跑几遍dijkstra,不T才叫神奇。
言归正传,这道题由于它的前提是使得最高温度最低的情况下消耗的热量尽量少,那么我们就可以先在边读进来后按温度从小到大排序,然后从最低温开始用最小生成树的克鲁斯卡尔算法加边,直到将s和t连通为止,这时的边的温度即为最低的最高温度,于是我们就可以用dijkstra跑一遍从s到t的最短路,求出来的dis[t]即为最低热量。
这里有一个易错点:算出最高温度后要把最高温度的所有边加进去,不然最短路算出来可能不对。
代码:
#include
using namespace std;
const int Max=2001000;
long long n,m,s,t,p;
long long dis[Max];
long long first[Max],father[Max];
bool exist[Max];
struct shu{int x,y,t,c;long long len;}; //注意len要用long long
shu bian[Max];
struct running{int to,next;long long len;}; //注意len要用long long
running size[Max];
inline int get_int()
{
int x=0,f=1;
char c;
for(c=getchar();(!isdigit(c))&&(c!='-');c=getchar());
if(c=='-') {f=-1;c=getchar();}
for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+c-'0';
return x*f;
}
inline bool comp(const shu &a,const shu &b) //将边按温度从小到大排序
{
return a.tb ? a : b;
}
*/
inline bool tense(long long &a,long long b) //相当于如果a>b则将b赋给a,比if快
{
return a > b ? (a=b , true) : false;
}
inline void dijstra() //用dijkstra算s到t的最短路
{
priority_queue >q;
memset(dis,0x3f,sizeof(dis));
memset(exist,0,sizeof(exist));
dis[s]=0;
q.push(make_pair(0,s));
exist[s]=1;
while(!q.empty())
{
int point=q.top().second;
q.pop();
exist[point]=1;
if(point==t) return;
for(int u=first[point];u;u=size[u].next)
if((tense(dis[size[u].to],dis[point]+size[u].len))&&(!exist[size[u].to]))
q.push(make_pair(-dis[size[u].to],size[u].to));
}
}
int main()
{
//freopen("running.in","r",stdin);
//freopen("running","w",stdout);
n=get_int();
m=get_int();
for(register int i=1;i<=n;i++) father[i]=i; //初始化
for(register int i=1;i<=m;i++)
{
bian[i].x=get_int();
bian[i].y=get_int();
bian[i].t=get_int();
bian[i].c=get_int();
bian[i].len=(long long)bian[i].t*bian[i].c;
}
s=get_int();
t=get_int();
sort(bian+1,bian+m+1,comp);
int highest=0;
for(register int i=1;i<=m;i++) //克鲁斯卡尔
{
int fax=getfather(bian[i].x);
int fay=getfather(bian[i].y);
if(fax!=fay)
{
father[fax]=fay;
highest=bian[i].t;
}
if(!(getfather(s)^getfather(t))) break;
}
for(register int i=1;i<=m;i++) //建边
if(bian[i].t<=highest)
{
build(bian[i].x,bian[i].y,bian[i].len);
build(bian[i].y,bian[i].x,bian[i].len);
}
dijstra();
cout< 后记:
这道题由于数据量及数据范围巨大,用不加任何优化的正解方法也会T,于是我开始对程序不断优化,这是我的提交记录(惨):
不过我也学到了不少优化的技巧:
1.读入优化:
初级读入优化:
inline int get_int()
{
int x=0,f=1;
char c;
for(c=getchar();(!isdigit(c))&&(c!='-');c=getchar());
if(c=='-') {f=-1;c=getchar();}
for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+c-'0';
return x*f;
}高级读入优化:
inline char read() {
static const int IN_LEN = 1024 * 1024;
static char buf[IN_LEN], *s, *t;
if (s == t) {
t = (s = buf) + fread(buf, 1, IN_LEN, stdin);
if (s == t) return -1;
}
return *s++;
}
template
inline void R(T &x) {
static bool iosig;
static char c;
for (iosig = false, c = read(); !isdigit(c); c = read()) {
if (c == -1) return ;
if (c == '-') iosig = true;
}
for (x = 0; isdigit(c); c = read()) x = ((x << 2) + x << 1) + (c ^ '0');
if (iosig) x = -x;
} 当然也听说过有3KB的神犇级别的读入优化,不过我想也没人会在考场上打吧。。。
2. inline,register
卡常数必备,我曾经尝试过加register降了一百多毫秒,但要注意了register不要加太多,只用加在核心部分的循环中就行了,效果也最明显。
3.该程序中的功能类型max的函数以及比较赋值的函数
4.O2优化
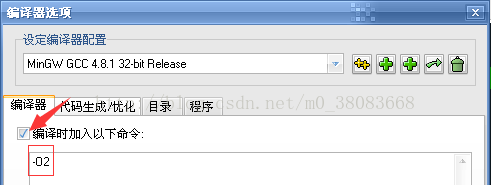
加O2优化编译能提高本机运行的速度,但正规比赛中测试机器是不会开O2优化的,所以O2优化的主要作用还是在考场上节约对拍的时间。
O2优化读图所示: