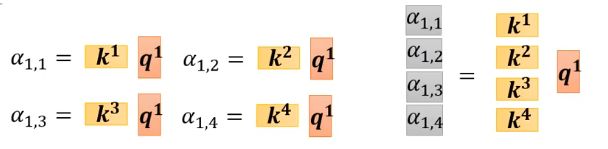【论文阅读笔记】《Attention is All You Need》——Attention机制和Transformer
Self-Attention
原理
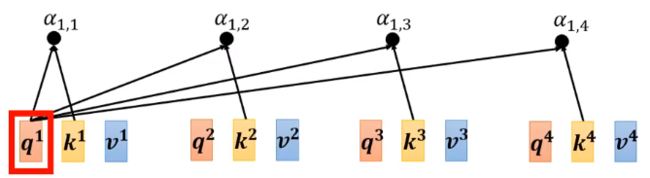
- 计算两个向量之间的相关性α
输 入 的 向 量 分 别 乘 矩 阵 W q 和 W k 得 到 q ( q u e r y ) 和 k ( k e y ) 输入的向量分别乘矩阵W^q和W^k得到q(query)和k(key) 输入的向量分别乘矩阵Wq和Wk得到q(query)和k(key)
相 似 度 α = q ⋅ k 相似度\alpha =q\cdot k 相似度α=q⋅k
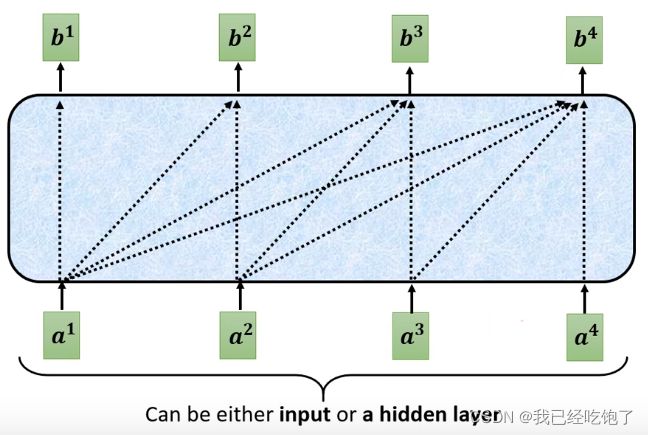
- Self-attention
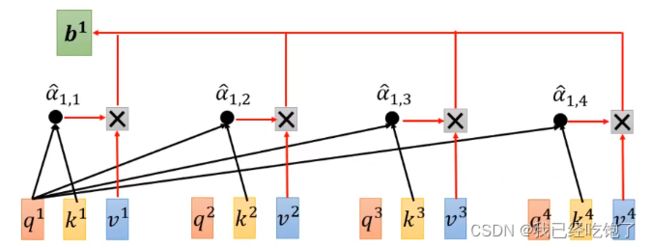
得 到 相 似 度 α , 也 就 是 权 重 , 和 每 个 向 量 的 v a l u e 相 乘 再 求 和 得 到 b 1 得到相似度\alpha,也就是权重,和每个向量的value相乘再求和得到b^1 得到相似度α,也就是权重,和每个向量的value相乘再求和得到b1
所 谓 s e l f , 是 a 1 自 己 也 会 与 自 己 求 一 个 权 重 α 1 , 1 ′ 所谓self,是a^1自己也会与自己求一个权重\alpha ^{'}_{1,1} 所谓self,是a1自己也会与自己求一个权重α1,1′
其 他 向 量 也 是 如 此 , 最 终 得 到 一 组 新 的 序 列 b 1 , b 2 , b 3 , b 4 其他向量也是如此,最终得到一组新的序列b^1,b^2,b^3,b^4 其他向量也是如此,最终得到一组新的序列b1,b2,b3,b4
所 以 s e l f − a t t e n t i o n 相 比 于 R N N 有 一 个 好 处 : 它 是 并 行 的 , b 1 , b 2 , b 3 , b 4 同 时 计 算 出 来 所以self-attention相比于RNN有一个好处:它是并行的,b^1,b^2,b^3,b^4同时计算出来 所以self−attention相比于RNN有一个好处:它是并行的,b1,b2,b3,b4同时计算出来
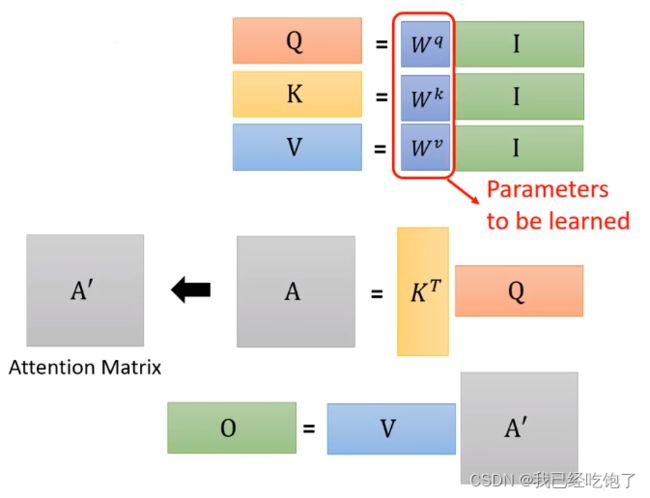
- 从矩阵乘法的角度
每 一 个 a 都 要 分 别 产 生 q , k , v 每一个a都要分别产生q,k,v 每一个a都要分别产生q,k,v
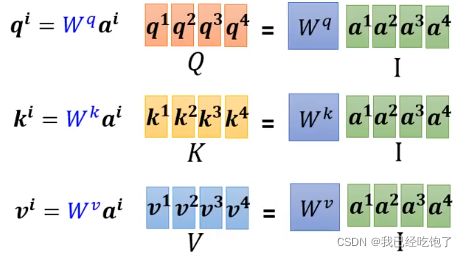
将 a t t e n t i o n 的 输 入 a 1 , a 2 , a 3 , a 4 拼 起 来 作 为 矩 阵 I , 分 别 成 W q , W k , W v , 得 到 矩 阵 Q , K , V 将attention的输入a^1,a^2,a^3,a^4拼起来作为矩阵I,分别成W^q,W^k,W^v,得到矩阵Q,K,V 将attention的输入a1,a2,a3,a4拼起来作为矩阵I,分别成Wq,Wk,Wv,得到矩阵Q,K,V
2. 计算权重α
[ k i ] T 拼 一 起 乘 q 1 , 得 到 的 、 a l p h a 矩 阵 是 输 入 a 1 和 其 他 向 量 的 相 关 性 , 其 他 输 入 同 理 [k^i]^T拼一起乘q^1,得到的、alpha矩阵是输入a^1和其他向量的相关性,其他输入同理 [ki]T拼一起乘q1,得到的、alpha矩阵是输入a1和其他向量的相关性,其他输入同理
用 s o f t m a x 对 每 一 列 进 行 归 一 化 , 用 其 他 方 法 比 如 R e l u 也 可 以 用softmax对每一列进行归一化,用其他方法比如Relu也可以 用softmax对每一列进行归一化,用其他方法比如Relu也可以

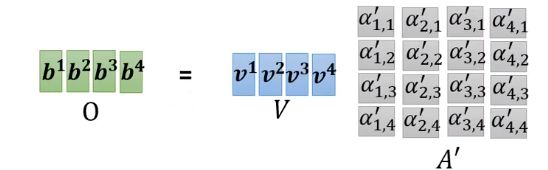
矩 阵 O 即 为 S e l f − a t t e n t i o n 的 输 出 矩阵O即为Self-attention的输出 矩阵O即为Self−attention的输出
这时候能发现Dot-Product(点积)计算的都是Query,Key等长的情况,而Addictive(加形)可以处理不等长的情况。Transformer中用的是Scaled Dot-Product Attention,和Dot-Product类似
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQKT)V
dk是K的维度,当维度很大时(Transformer里dk=512),两个向量做点积的结果也会比较大或者比较小,所以经过Softmax后的会更加靠近1或0,即值会更加向两端靠拢,在梯度下降的时候梯度较小,算的会比较慢。
- 总结
只 有 W q , W k , W v 是 需 要 通 过 训 练 学 出 来 的 只有W^q,W^k,W^v是需要通过训练学出来的 只有Wq,Wk,Wv是需要通过训练学出来的
-
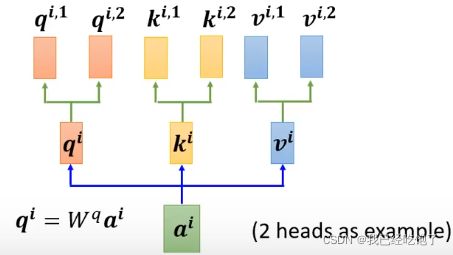
Multi-head Self-attention 多头注意力机制
个人理解:self-attention就是用每个向量的q去寻找相关的k,但是”相关“这件事情,本身就有很多种,所以我们需要不同的q去负责不同种类的“相关性”。
q i , 1 = W q , 1 q i q^{i,1}=W^{q,1}q^i qi,1=Wq,1qi
q i , 2 = W q , 2 q i q^{i,2}=W^{q,2}q^i qi,2=Wq,2qi
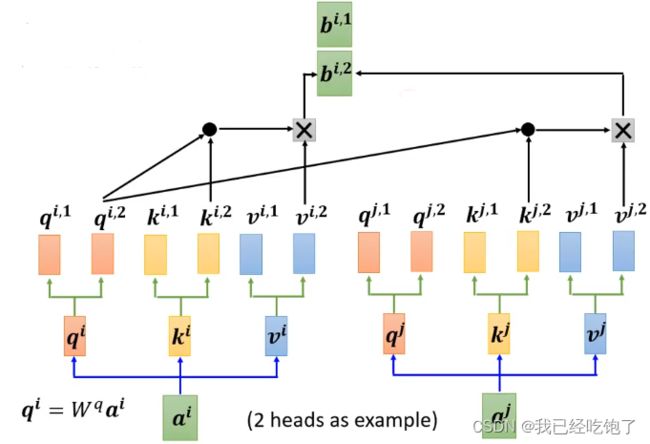
q i , 1 只 管 k i , 1 和 k j , 1 q^{i,1}只管k^{i,1}和k^{j,1} qi,1只管ki,1和kj,1
同 理 同理 同理
最 后 得 到 输 出 b i 最后得到输出b^i 最后得到输出bi

-
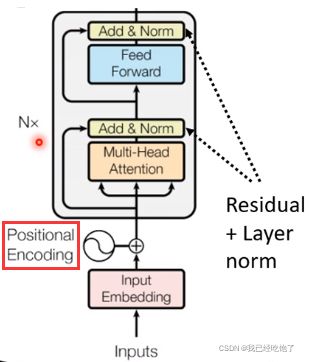
Positional Encoding
这样的Self-attention有个缺点:它没有包含位置信息,即输入的向量在前面或是在后面都没有区别。所以引入了Positional Encoding,为每个位置设定一个向量e
这是怎么加的,值硬加?
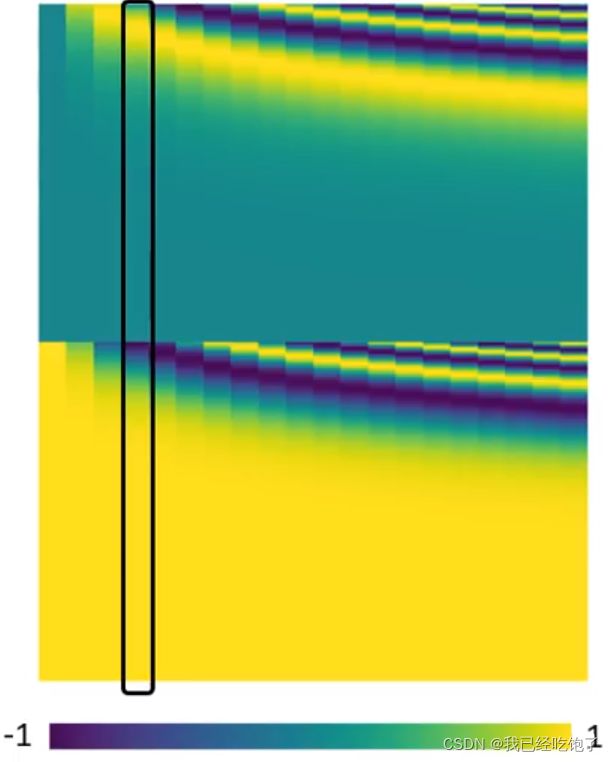
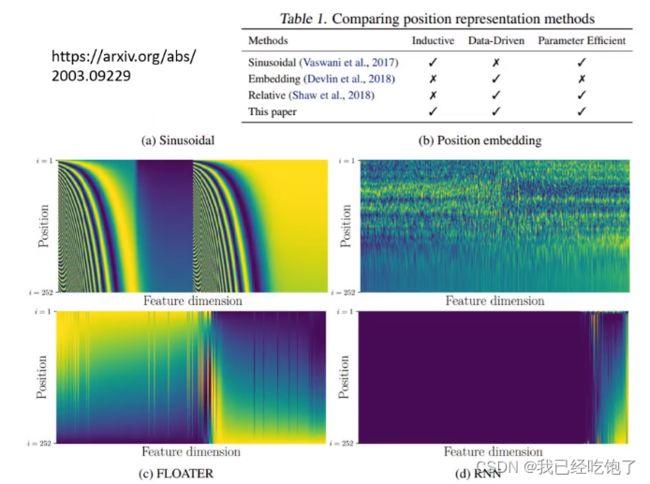
《Attention is all you need》里的Positional Encoding,每一列代表一个e,通过sin cos 一系列规则制定出来的(见后文)
Positional Encoding可以是认为通过某个函数制定的,也可以是训练出来的,一些其他的位置编码形式:
Self-attention应用
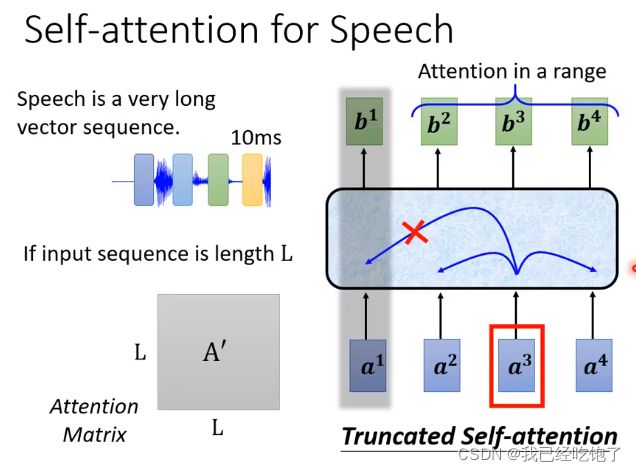
用Self-attention做语音识别
在语音识别领域,通常10ms就会产生一个向量,所以一句话能产生的向量的数量是非常大的,那么在计算权重矩阵A‘时。这个矩阵就会非常大(L*L,L为输入向量的个数),所以我们采取Truncated Self-attention,即不用和其他所有的向量都做Attention,只需要和某个范围内的向量做即可(看上面矩阵手算一下维度,容易推出A’的大小),这个范围是人为确定的。
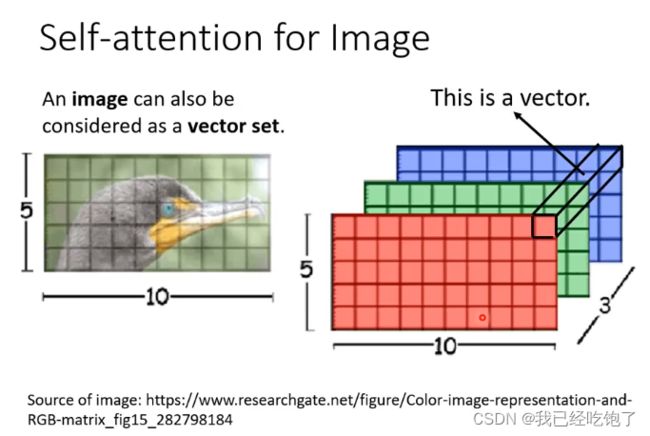
用Self-attention做图像处理
每 个 像 素 是 一 个 三 维 ( R G B ) 的 向 量 每个像素是一个三维(RGB)的向量 每个像素是一个三维(RGB)的向量
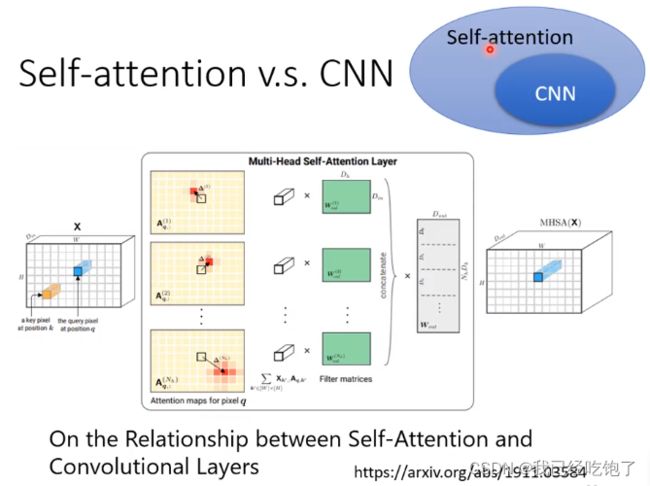
Self-attention和CNN
CNN只考虑了感受野范围内像素之间的关系,而Self-attention考虑了全局像素之间的联系,而且Self-attention中的感受野是自动学习出来的,并不是人为规定了感受野的形状。CNN是Self-attention青春版。
而像Self-attention这种灵活的模型,就需要更大的数据量,否则就会产过拟合,但CNN在小数据量时就能产生不错的效果。
Self-attention和RNN
RNN的hard to consider意思是距离太远的向量,传递信息很麻烦LSTM、GRU,但Self-attention所有的向量“天涯若比邻”。
RNN不能并行,Self-attention可以并行,效率高。
论文《Transformers are RNNs: Fast Autoregressive Transformer with Linear》
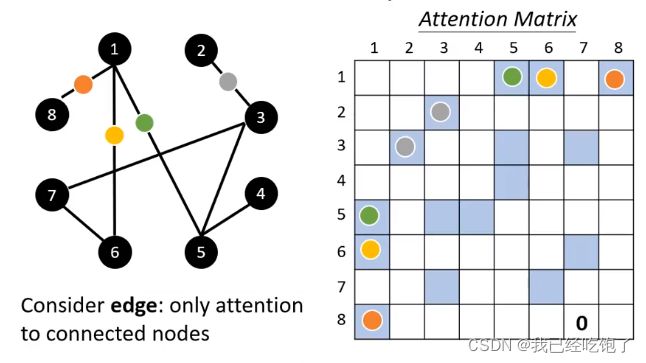
Self-attention用在图上
已经帮Self-attention筛选过了向量之间的关系。只需要计算互相连接的点的Attention Score
这也是图神经网络GNN的一种。
Transformer
模型架构:
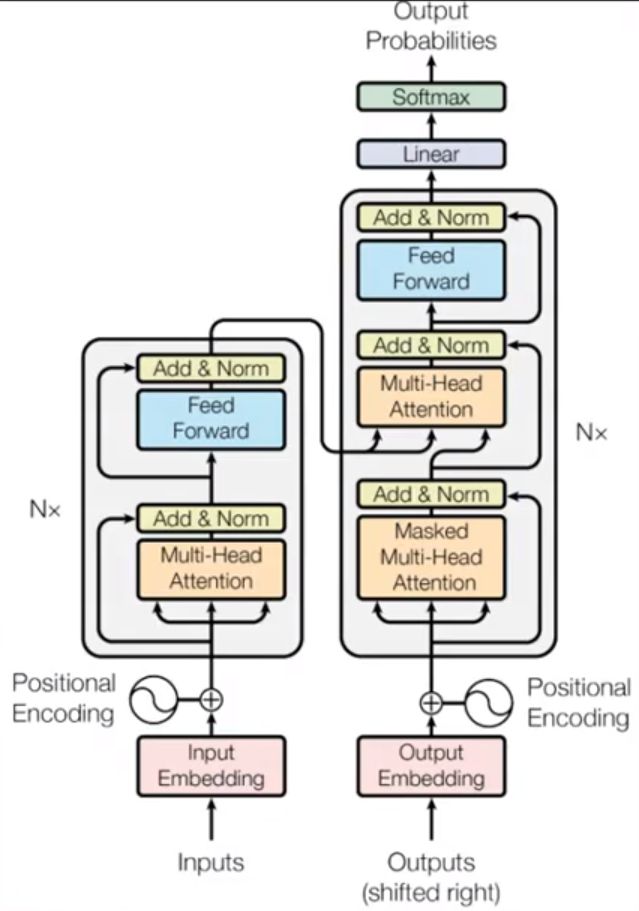
左侧Encoder,右侧Decoder,本质上也是seq2seq模型
Encoder
其中经过了n层block
每一层block的工作:进行Self-attention,得到输出送进Fully Connected(FC)
但实际上Transformer更加复杂一些,做了一步残差连接,之后进行了归一化Normlization
Layer-Normlization
Transformer没有使用Batch-Normlization ,而是Layer-Normlization
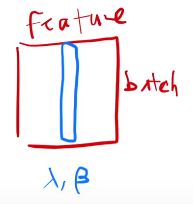
把 每 一 个 特 征 进 行 归 一 化 ( 均 值 为 0 , 方 差 为 1 ) , 也 可 以 学 到 λ , β , 用 来 调 整 成 任 意 的 方 差 和 均 值 。 把每一个特征进行归一化(均值为0,方差为1),也可以学到 λ,β ,用来调整成任意的方差和均值。 把每一个特征进行归一化(均值为0,方差为1),也可以学到λ,β,用来调整成任意的方差和均值。
在 训 练 时 对 每 个 m i n i − b a t c h 进 行 归 一 化 , 在 预 测 是 还 要 有 一 个 全 局 的 均 值 和 方 差 的 计 算 在训练时对每个mini-batch进行归一化,在预测是还要有一个全局的均值和方差的计算 在训练时对每个mini−batch进行归一化,在预测是还要有一个全局的均值和方差的计算
- Layer Norm:对 行(即样本)进行归一化
在三维空间看来如图

选择LN而不是BN的原因:由于样本中序列的长度并不是一样的。
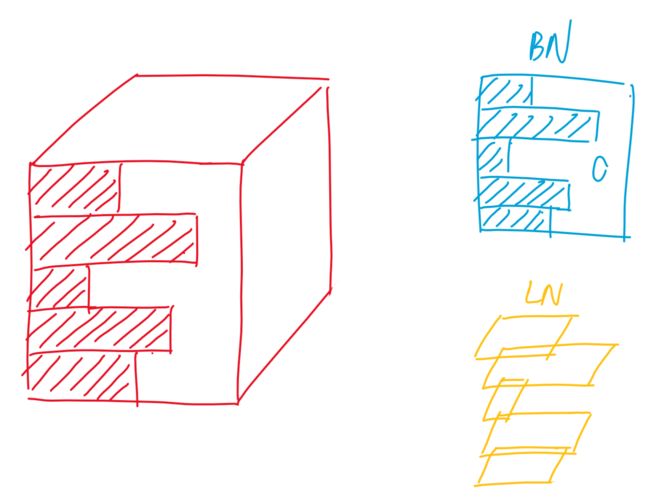
对于BN,如果样本长度变化比较大,那么每次计算小批量的均值和方差的抖动是比较大的。而且在预测时要把全局的均值和方差记录下来,如果这是出现了一个非常长的样本,是我在训练时没有碰到的,那前面算的均值和方差可能就不好用了。
而LN是每个样本自己内部算均值和方差,也不需要存全局的均值和方差,所以稳定一些。
Position-wise Feed-Forward Networks
这时得到的输出才是Fully Connected的输入,同样地,Fully Connected也有残差连接以及Layer-Normlization操作,最后才得到了一层block的输出。
Fully Connected都干了什么呢?
Position-wise Feed-Forward Networks,本质上就是一个MLP,不同的是,对每一个词作用的是同样的MLP,即Point-wise的意思。
F F N ( x ) = m a x ( 0 , x W 1 + b 1 ) W 2 + b 2 FFN(x)=max(0,xW_1+b_1)W_2+b_2 FFN(x)=max(0,xW1+b1)W2+b2
具体来看
x W 1 + b 1 线 性 层 xW_1+b_1 \ \ \ \ 线性层 xW1+b1 线性层
m a x ( 0 , x W 1 + b 1 ) R e L U 激 活 层 max(0,xW_1+b_1) \ \ \ \ ReLU激活层 max(0,xW1+b1) ReLU激活层
m a x ( 0 , x W 1 + b 1 ) W 2 + b 2 线 性 层 max(0,xW_1+b_1)W_2+b_2\ \ \ \ 线性层 max(0,xW1+b1)W2+b2 线性层
x 是 长 度 为 512 的 向 量 , W 1 把 512 投 影 成 2048 , 由 于 之 后 还 要 进 行 残 差 连 接 , W 2 再 把 2048 投 影 回 512 , x是长度为512的向量,W_1把512投影成2048,由于之后还要进行残差连接,W_2再把2048投影回512, x是长度为512的向量,W1把512投影成2048,由于之后还要进行残差连接,W2再把2048投影回512,
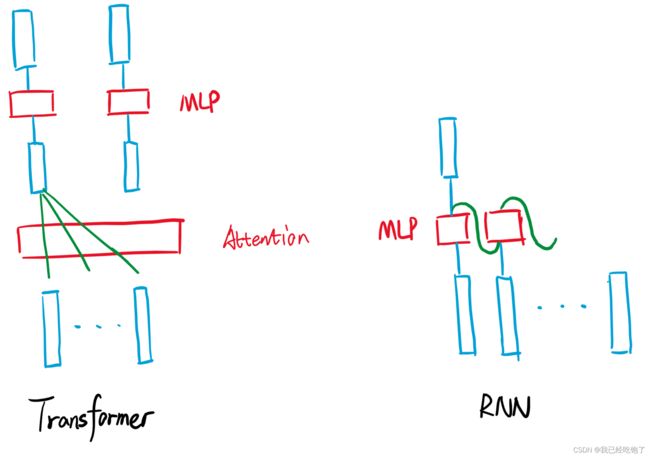
和RNN的区别
Transformer:Attention对输入序列的信息进行抓取进行汇聚,所以后面用MLP,想要映射到我想要的语义空间中时,每个MLP只需要独立对每个点进行处理就行了,因为每个向量都包含了整个序列的信息。
RNN:序列的信息是一步一步传递的。
关注点都是如何有效使用整个序列的信息。
Positional Encoding
再回过来看Encoder的架构图,在输入时添加了前面说过的位置编码。
首先在Transformer中,输入的向量的长度是512,所以位置编码的向量长度也是512。
P E ( p o s , 2 i ) = s i n ( p o s / 1000 0 2 i / d m o d e l ) P E ( p o s , 2 i + 1 ) = c o s ( p o s / 1000 0 2 i / d m o d e l ) PE_{(pos,2i)}=sin(pos/10000^{2i/d_{model}})\\PE_{(pos,2i+1)}=cos(pos/10000^{2i/d_{model}}) PE(pos,2i)=sin(pos/100002i/dmodel)PE(pos,2i+1)=cos(pos/100002i/dmodel)
然后相加。
❓后续的模块看到这个输入是怎么判断这个词的位置信息的呢?
当然,Encoder的设计也不是唯一的,上述内容是原始论文提出的Encoder架构,也有论文《On Layer Normalization in the Transformer Architecture》把block中的一些操作顺序换了换,得到了更好的结果。
以及为什么选Layer-Normalization而不是Batch-Normalization,也有论文《Powernorm: Rethinking Batch Normalization in Transformers》还提出了Powernorm
Decoder
——Autoregressive(AT)
接下来都以语音识别为例。
在Encoder产生向量之后,输入到Decoder中,并且Decoder也有自己的输入,个人感觉个RNN类似,将上一步的输出作为下一步的输入。
Decoder的结构
Masked Multi-Head Attention
将Decoder和Encoder的结构相比较一下
会发现除去红框位置的部分,其余结构Encoder和Decoder几乎是一样的,唯一差别在于 Encoder 采用的是 Multi-Head Attention 而Dcoder 采用的是 Masked Multi-Head Attention
因为Decoder的输入并不像Encoder一样是并行的,所以在做Self-attention时,前面的输入是看不到后面输入的,只能看见前面已经有的输入,所以叫 Masked Multi-Head Attention
更详细一点
在 产 生 b 2 时 , 只 能 拿 q 2 与 k 1 和 k 2 分 别 对 比 计 算 相 似 度 在产生b^2时,只能拿q^2与k^1和k^2分别对比计算相似度 在产生b2时,只能拿q2与k1和k2分别对比计算相似度
在Transformer中,是将q,k点积的值换成非常大的负数,其做softmax的指数的时候,softmax的结果就会变成0,权重变为0
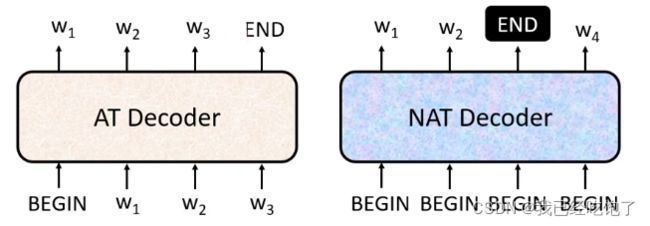
这也是Autoregressive(AT)这种Decoder的缺点:不能并行,另一种Decoder:Non-Autoregressive(NAT)则是并行的
那么怎么判断什么时候结束输出呢?
-
对于AT来说,等到softmax计算出输出END的概率最大时,就可以停止了。
-
但对于NAT,由于并行输入的是一堆BEGIN,所以并不能判断输出的序列到底是多长,所以:
- 另外还有一个分类器,Encoder的输出作为输入,输出一个数字,就是Decoder应该输出序列的长度
- 假设一个非常大的长度,最后忽略END后面的输出。(如果我都能知道输出有END了,我为什么还要接着输出呢?)
而且NAT还可以控制输出的长度。但是从效果上来说NAT还是不如AT。因为存在着multi-modality这个问题
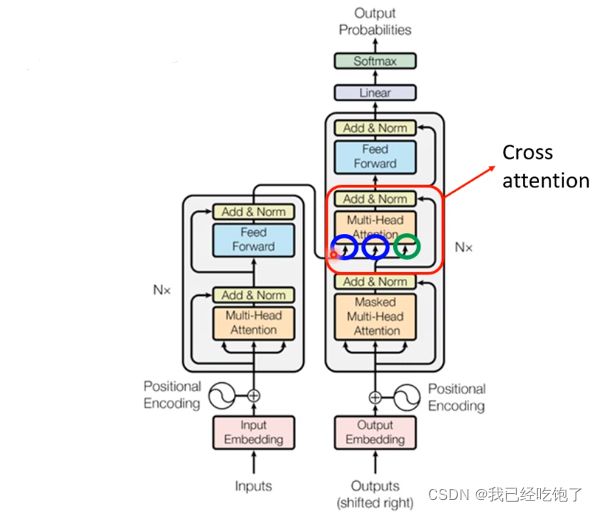
Cross attention
Encoder和Decoder连接(Cross attention)
Encoder提供两个输入(k,v),Decoder提供一个输入(q)
简单来说就是Encoder和Decoder做Attention,没有self哦~
Decoder的其他输出词也是如此
模型比较
n:序列的长度
d:向量的长度
Complexity per Layer:计算复杂度 (主要是Query矩阵和Key矩阵做内积)
Sequential Operations:顺序的计算,即下一步计算必须等待前面多少不计算完成,也就是并行度。
Maximum Path Length:信息从一点走到另一点的距离,是不是“天涯若比邻的”
Tips
Guided Attention
基于对问题本身的理解,强迫Attention有一个固定的样貌,比如语音识别,就应该是由左向右的顺序
Beam Search
让Decoder产生一些随机性,个人理解类似优化算法中跳出局部最优解
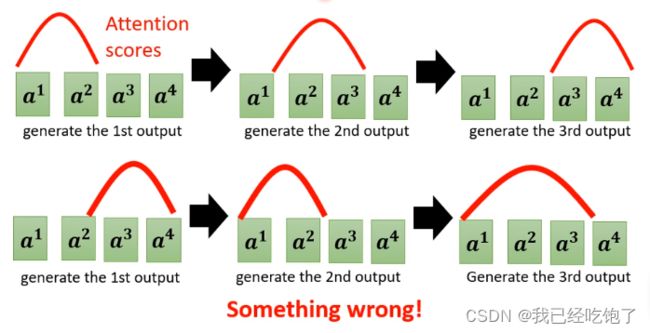
训练的时候Decoder的输入都是正确的(如右图),但在测试时,可能会产生一步错步步错的问题。所以在训练时偶尔喂给Decoder一些错误的东西反而训练效果会更好(Scheduled Sampling)。
疑问:
1. 残差连接的作用
2. 位置编码是怎么都后续模块识别的,直接加不会影响词向量本身的信息吗?