利用 python 编写 K-Means聚类算法
利用 python 实现 K-Means聚类
一.k-means聚类算法简介
(一)k-means聚类算法的概念
k-means算法是很典型的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
k个初始类聚类中心点的选取对聚类结果具有较大的影响,因为在该算法第一步中是随机的选取任意k个对象作为初始聚类的中心,初始地代表一个簇。该算法在每次迭代中对数据集中剩余的每个对象,根据其与各个簇中心的距离将每个对象重新赋给最近的簇。当考察完所有数据对象后,一次迭代运算完成,新的聚类中心被计算出来。如果在一次迭代前后,J的值没有发生变化,说明算法已经收敛。
(二)对k-means算法的认识
1.优点
(1)算法快速、简单。
(2)对大数据集有较高的效率并且是可伸缩性的。
(3)时间复杂度近于线性,而且适合挖掘大规模数据集。K-Means聚类算法的时间复杂度是O(nkt) ,其中n代表数据集中对象的数量,t代表着算法迭代的次数,k代表着簇的数目。
2.缺点
(1)聚类是一种无监督的学习方法,在 K-means 算法中 K 是事先给定的,K均值算法需要用户指定创建的簇数k,但这个 K 值的选定是非常难以估计的。
(2)在 K-means 算法中,首先需要根据初始聚类中心来确定一个初始划分,然后对初始划分进行优化。这个初始聚类中心的选择对聚类结果有较大的影响,一旦初始值选择的不好,可能无法得到有效的聚类结果,这也成为 K-means算法的一个主要问题。
(3)从 K-means 算法框架可以看出,该算法需要不断地进行样本分类调整,不断地计算调整后的新的聚类中心,因此当数据量非常大时,算法的时间开销是非常大的。所以需要对算法的时间复杂度进行分析、改进,提高算法应用范围,而这导致K均值算法在大数据集上收敛较慢。
二.算法过程
1.选取k个初始聚类中心点
2. 计算每个点与各簇中心点的欧氏距离
3. 根据每个点与各个簇中心的距离将每个对象重新赋给最近的簇
3. 更新簇的中心点
4. 迭代,直到收敛(通常停止迭代的条件: 簇的中心点不再发生明显的变化,即收敛)
三.设计思想
1.利用pandas和numpy将CSV中的数据导入到python中,并转化成多维向量。
2.先通过观察所有点的分布来确定k的取值,将导入到python中的所有坐标值通过彩虹色来实现对k值的初步判断。
3. 选取k=3,随机选择三个中心点,计算所有值到簇中心点的距离并根据每个点与各个簇中心的距离将每个对象重新赋给距离最近的簇。
4.对新生成的簇的所有值求平均值来获得新的簇中心点。
5.通过递归重复3、4两步,直至簇的中心点不再发生明显的变化。
6.生成迭代停止后的散点图,以及各簇中所包含的点。
四.实现代码
鸢尾花数据集共有四个属性,为展示算法,只采用其中三个属性帮助大家理解。
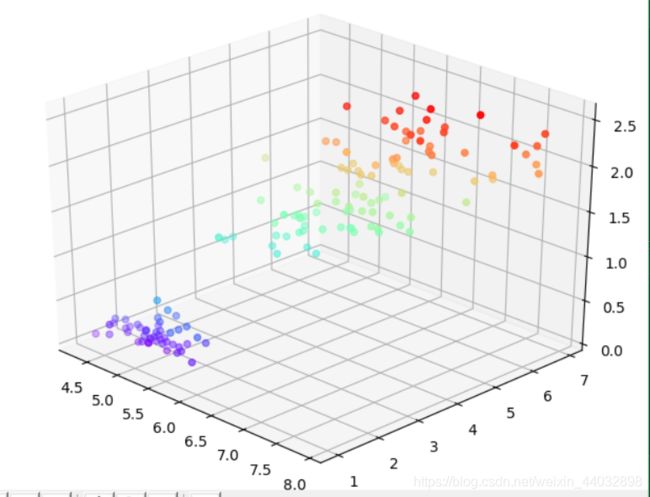
这一部分的代码是将数据集中的所有点按照彩虹色画出来;先通过观察所有点的分布来确定k的取值。
#导入模块
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import os
#设置工作路径
os.chdir('d:/workpath')
#利用pandas和numpy将CSV中的数据导入到python中
df = pd.read_csv('d:\iris.csv',header=None)
content=pd.DataFrame(df,columns=[0,1,2,3])
a=np.array(content)
#创建绘制三维图的环境
fig = plt.figure()
ax = Axes3D(fig)
#绘制图像
ax.scatter(content[0], content[2], content[3],c=content[3],cmap='rainbow')
#调整观察角度和方位角。这里将俯仰角设为30度,把方位角调整为-45度
ax.view_init(30, -45)
plt.show()
根据图1显示所有的值的分布可以将数据大致可以分为三类,所以我们取k=3来进行聚类分析。
利用kmean方法进行聚类,将聚类结果输出到out_file.txt中,并将不同的类型的点按不同颜色画在坐标系中,
#生成空矩阵用于存储各簇的数据
b=np.zeros(0)
c=np.zeros(0)
d=np.zeros(0)
#随机选择三个中心点,计算所有值到中心点的距离
for i in range(0,len(a)):
dis1=np.linalg.norm(a[i:i+1]-a[7:8])
dis2=np.linalg.norm(a[i:i+1]-a[99:100])
dis3=np.linalg.norm(a[i:i+1]-a[112:113])
# 根据每个点与各个簇中心的距离将每个对象重新赋给最近的簇
if min(dis1,dis2,dis3)==dis1:
b=np.append(b,a[i:i+1])
x=int(len(b)/4)
b=np.reshape(b,newshape=(x,4))
if min(dis1,dis2,dis3)==dis2:
c=np.append(c,a[i:i+1])
x=int(len(c)/4)
c=np.reshape(c,newshape=(x,4))
if min(dis1,dis2,dis3)==dis3:
d=np.append(d,a[i:i+1])
x=int(len(d)/4)
d=np.reshape(d,newshape=(x,4))
#对新生成的簇的所有值求平均值来获得新的簇中心点
b=np.mean(b,axis=0)
c=np.mean(c,axis=0)
d=np.mean(d,axis=0)
#创建k_mean函数
def k_mean(b,c,d):
#储存新的簇中的所有点
list1 = []
list2 = []
list3 = []
#储存新的簇中心点
gap1 = b
gap2 = c
gap3 = d
#生成空矩阵用于存储各簇的数据
b = np.zeros(0)
c = np.zeros(0)
d = np.zeros(0)
#计算所有值到新的簇中心点的距离
for i in range(0,len(a)):
dis1=np.linalg.norm(a[i:i+1]-gap1)
dis2=np.linalg.norm(a[i:i+1]-gap2)
dis3=np.linalg.norm(a[i:i+1]-gap3)
# 根据每个点与各个簇中心的距离将每个对象重新赋给最近的簇
if min(dis1, dis2, dis3) == dis1:
list1.append(i)
b = np.append(b, a[i:i + 1])
x = int(len(b) / 4)
b = np.reshape(b, newshape=(x, 4))
if min(dis1, dis2, dis3) == dis2:
list2.append(i)
c = np.append(c, a[i:i + 1])
x = int(len(c) / 4)
c = np.reshape(c, newshape=(x, 4))
if min(dis1, dis2, dis3) == dis3:
list3.append(i)
d = np.append(d, a[i:i + 1])
x = int(len(d) / 4)
d = np.reshape(d, newshape=(x, 4))
#将新生成的簇的所有值转化为多维向量
line1= pd.DataFrame(b)
line2=pd.DataFrame(c)
line3=pd.DataFrame(d)
#对新生成的簇的所有值求平均值来获得新的簇中心点
b=np.mean(b,axis=0)
c=np.mean(c,axis=0)
d=np.mean(d,axis=0)
#当簇的中心点不再发生明显的变化时停止递归
if abs(sum(b - gap1))+abs(sum(c - gap2))+abs(sum(d - gap3))<10**(-64):
# 创建out_file用于存储输出结果
out_file = open('out_file.txt', 'w')
out_file.write('Setosa\n')
out_file.writelines(str(list1))
out_file.write('\nVersicolor\n')
out_file.writelines(str(list2))
out_file.write('\nVirginica\n')
out_file.writelines(str(list3))
# 三维散点的数据
x1 = line1[0]
y1 = line1[2]
z1 = line1[3]
x2 = line2[0]
y2 = line2[2]
z2 = line2[3]
x3 = line3[0]
y3 = line3[2]
z3 = line3[3]
#创建绘制三维图的环境
fig = plt.figure()
ax = Axes3D(fig)
# 绘制散点图
ax.scatter(x1, y1, z1,cmap='Blues',label='Setosa')
ax.scatter(x2, y2, z2,c='g',label='Versicolor',marker='D')
ax.scatter(x3, y3, z3,c='r',label='Virginica')
ax.legend(loc='best')
# 调整观察角度和方位角。这里将俯仰角设为30度,把方位角调整为-45度
ax.view_init(30, -45)
plt.show()
#当簇的中心点发生明显的变化时继续递归k_mean函数
else:
gap1=b
gap2=c
gap3=d
return k_mean(b,c,d)
#运行k_mean函数
k_mean(b,c,d)
五.分析结果
随机选择三个中心点,计算所有值到簇中心点的距离并根据每个点与各个簇中心的距离将每个对象重新赋给距离最近的簇。并对新生成的簇的所有值求平均值来获得新的簇中心点。通过多次迭代获得最终的聚类结果如图2所示。
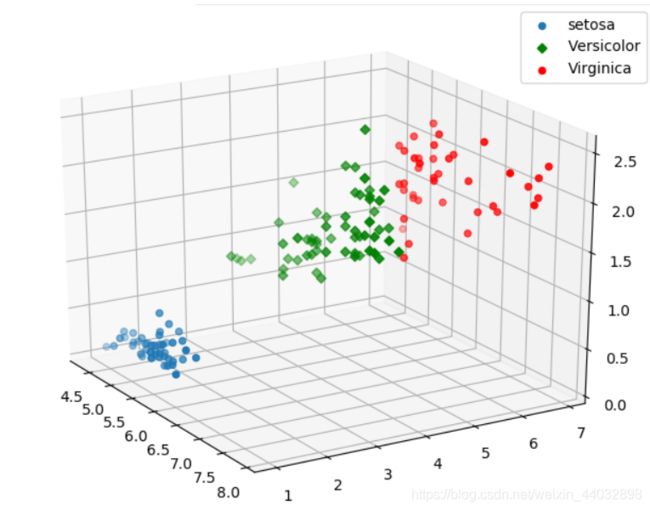
out_file.txt文件中的输出结果:
Setosa:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23,
24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44,
45, 46, 47, 48, 49]
Versicolor:
[51, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72,
73, 74, 75, 76, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94,
95, 96, 97, 98, 99, 101, 106, 113, 114, 119, 121, 123, 126, 127, 133, 138, 142,
146, 149]
Virginica:
[50, 52, 77, 100, 102, 103, 104, 105, 107, 108, 109, 110, 111, 112, 115, 116,
117, 118, 120, 122, 124, 125, 128, 129, 130, 131, 132, 134, 135, 136, 137,
139, 140, 141, 143, 144, 145, 147, 148]
通过输出的簇的各点可以看出聚类得到的结果和真实值存在一定的偏差,体现了 K-means 算法中的初始聚类中心的选择对聚类结果的影响。输出结果中有17个数据和原始数据的分类有区别,我们得到的结果和原始数据的相似率为89%。