《机器学习实战》学习笔记(四) : 朴素贝叶斯的基本原理
在看了书、CSDN上的博客、B站上的视频后整理而成,超级感谢前辈提供的宝贵知识~
Table of Contents
- 1 基础数学知识
- 1.1 条件概率公式
- 1.2 贝叶斯公式
- 1.3 全概率公式
- 1.4 实例:判断瓢虫是否会冬眠
- 2 使用朴素贝叶斯进行文档分类
- 2.1 原理理解
- 2.1.1 原始词条
- 2.1.2 词汇表
- 2.1.3 统计词条,生成词向量
- 2.1.4 计算概率
- 2.1.5 计算结果
- 2.2 python代码
- 2.2.1 函数loadDataSet:创建实验数据集
- 2.2.2 函数createVocabList:生成词汇表
- 2.2.3 函数setOfWords2Vec:生成词向量
- 2.2.4 函数get_trainMat:所有词条向量列表
- 2.2.5 函数trainNB:朴素贝叶斯分类器训练函数
- 2.2.6 函数classifyNB:朴素贝叶斯分类函数
- 2.2.7 函数testingNB:朴素贝叶斯测试函数
- 2.2.8 拉普拉斯平滑
- 2.2.9 文档词袋模型
- 2.3 更完整的实例:过滤垃圾邮件
- 2.3.1 函数:textParse文本切分
- 2.3.2 函数:getData获得全部数据集
- 2.3.3 函数:划分数据集和测试集
- 2.3.4 函数:训练朴素贝叶斯分类器
- 2.1 原理理解
基础数学知识
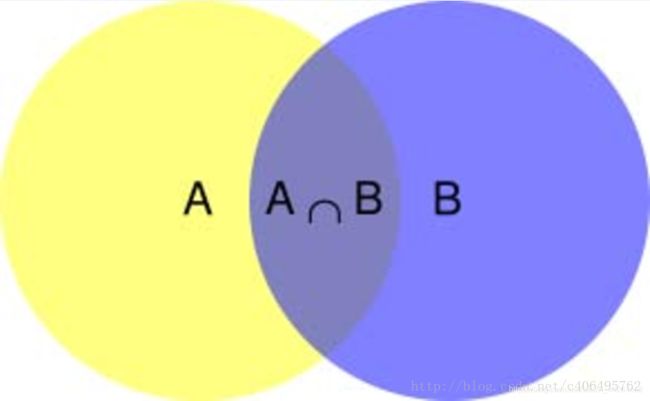
条件概率公式
P ( A ∩ B ) = P ( A ∣ B ) P ( B ) P(A\cap B)=P(A|B)P(B) P(A∩B)=P(A∣B)P(B)
P ( A ∩ B ) = P ( B ∣ A ) P ( A ) P(A\cap B)=P(B|A)P(A) P(A∩B)=P(B∣A)P(A)
由此可以得到
P ( A ∣ B ) = P ( A ) P ( B ∣ A ) P ( B ) P(A|B) = \frac{P(A)P(B|A)}{P(B)} P(A∣B)=P(B)P(A)P(B∣A)
即贝叶斯公式
贝叶斯公式
其中, P ( A ) P(A) P(A)为先验概率, P ( A ∣ B ) P(A|B) P(A∣B)为后验概率, P ( B ∣ A ) P ( B ) \frac{P(B|A)}{P(B)} P(B)P(B∣A)为调整因子
全概率公式
KaTeX parse error: No such environment: align at position 9: \begin{̲a̲l̲i̲g̲n̲}̲ P(B) &=P(BA_1…
所以贝叶斯公式又可以写为
P ( A i ∣ B ) = P ( A i ) P ( B ∣ A i ) ∑ i = 1 n P ( B ∣ A i ) P ( A i ) P(A_i|B) = \frac{P(A_i)P(B|A_i)}{\sum_{i=1}^nP(B|A_i)P(A_i)} P(Ai∣B)=∑i=1nP(B∣Ai)P(Ai)P(Ai)P(B∣Ai)
在朴素贝叶斯中,贝叶斯公式转化为:
比如标签中一共有三个特征,我们要计算在具体某个特征下,为类别一的概率
P ( 类 别 一 ∣ 特 征 ) = P ( 特 征 ∣ 类 别 一 ) P ( 类 别 一 ) P ( 类 别 一 ∣ 特 征 ) P ( 类 别 一 ) + P ( 类 别 二 ∣ 特 征 ) P ( 类 别 二 ) + P ( 类 别 三 ∣ 特 征 ) P ( 类 别 三 ) P(类别一|特征)=\frac{P(特征|类别一)P(类别一)}{P(类别一|特征)P(类别一)+P(类别二|特征)P(类别二)+P(类别三|特征)P(类别三)} P(类别一∣特征)=P(类别一∣特征)P(类别一)+P(类别二∣特征)P(类别二)+P(类别三∣特征)P(类别三)P(特征∣类别一)P(类别一)
实例:判断瓢虫是否会冬眠
我们以判断瓢虫是否会冬眠为例,理解朴素贝叶斯的计算过程
数据集
import numpy as np
import pandas as pd
origin_data = {'温度':['零上','零上','零下','零下','零下'],'瓢虫的年龄':['10天','一个月','10天','一个月','一个月'],'瓢虫冬眠':['否','否','是','是','是']}
data = pd.DataFrame(origin_data)
data
| 温度 | 瓢虫的年龄 | 瓢虫冬眠 | |
|---|---|---|---|
| 0 | 零上 | 10天 | 否 |
| 1 | 零上 | 一个月 | 否 |
| 2 | 零下 | 10天 | 是 |
| 3 | 零下 | 一个月 | 是 |
| 4 | 零下 | 一个月 | 是 |
我们已知已知瓢虫是一个月大,零上,计算它会冬眠的概率
根据公式
P ( 类 别 一 ∣ 特 征 ) = P ( 类 别 一 ∣ 特 征 ) P ( 类 别 一 ) P ( 类 别 一 ∣ 特 征 ) P ( 类 别 一 ) + P ( 类 别 二 ∣ 特 征 ) P ( 类 别 二 ) P(类别一|特征)=\frac{P(类别一|特征)P(类别一)}{P(类别一|特征)P(类别一)+P(类别二|特征)P(类别二)} P(类别一∣特征)=P(类别一∣特征)P(类别一)+P(类别二∣特征)P(类别二)P(类别一∣特征)P(类别一)
得
P ( 冬 眠 ∣ 一 个 月 大 , 零 上 ) = P ( 一 个 月 大 , 零 上 ∣ 冬 眠 ) P ( 冬 眠 ) P ( 一 个 月 大 , 零 上 ∣ 冬 眠 ) P ( 冬 眠 ) + P ( 一 个 月 大 , 零 上 ∣ 不 冬 眠 ) P ( 不 冬 眠 ) P(冬眠|一个月大,零上)=\frac{P(一个月大,零上|冬眠)P(冬眠)}{P(一个月大,零上|冬眠)P(冬眠)+P(一个月大,零上|不冬眠)P(不冬眠)} P(冬眠∣一个月大,零上)=P(一个月大,零上∣冬眠)P(冬眠)+P(一个月大,零上∣不冬眠)P(不冬眠)P(一个月大,零上∣冬眠)P(冬眠)
其中 P ( 一 个 月 大 , 零 上 ∣ 冬 眠 ) P(一个月大,零上|冬眠) P(一个月大,零上∣冬眠),存在多个特征时如何计算呢?
我们假设每个标签都是独立的,也就是年龄是多少与温度没有半毛钱关系,有了这个假设后
P ( 一 个 月 大 , 零 上 ∣ 冬 眠 ) = P ( 一 个 月 大 ∣ 冬 眠 ) P ˙ ( 零 上 ∣ 冬 眠 ) P(一个月大,零上|冬眠) = P(一个月大|冬眠)\dot P(零上|冬眠) P(一个月大,零上∣冬眠)=P(一个月大∣冬眠)P˙(零上∣冬眠)
故
P ( 冬 眠 ∣ 一 个 月 大 , 零 上 ) = P ( 一 个 月 大 , 零 上 ∣ 冬 眠 ) P ( 冬 眠 ) P ( 一 个 月 大 , 零 上 ∣ 冬 眠 ) P ( 冬 眠 ) + P ( 一 个 月 大 , 零 上 ∣ 不 冬 眠 ) P ( 不 冬 眠 ) = P ( 冬 眠 ) P ( 一 个 月 大 ∣ 冬 眠 ) P ( 零 上 ∣ 冬 眠 ) P ( 冬 眠 ) P ( 一 个 月 大 ∣ 冬 眠 ) P ( 零 上 ∣ 冬 眠 ) + P ( 不 冬 眠 ) P ( 一 个 月 大 ∣ 不 冬 眠 ) P ( 零 上 ∣ 不 冬 眠 ) \begin{aligned} P(冬眠|一个月大,零上)& =\frac{P(一个月大,零上|冬眠)P(冬眠)}{P(一个月大,零上|冬眠)P(冬眠)+P(一个月大,零上|不冬眠)P(不冬眠)}\\ & =\frac{P(冬眠)P(一个月大|冬眠)P(零上|冬眠)}{P(冬眠)P(一个月大|冬眠)P(零上|冬眠)+P(不冬眠)P(一个月大|不冬眠)P(零上|不冬眠)}\\ \end{aligned} P(冬眠∣一个月大,零上)=P(一个月大,零上∣冬眠)P(冬眠)+P(一个月大,零上∣不冬眠)P(不冬眠)P(一个月大,零上∣冬眠)P(冬眠)=P(冬眠)P(一个月大∣冬眠)P(零上∣冬眠)+P(不冬眠)P(一个月大∣不冬眠)P(零上∣不冬眠)P(冬眠)P(一个月大∣冬眠)P(零上∣冬眠)
这也是朴素贝叶斯中朴素二字的由来,即使用贝斯叶公式时,假设各特征间相互独立,简化了计算。在特征之间关联度比较大的时候,朴素贝叶斯的效果很不好
总结下我们都需要哪些变量
- P(冬眠) P(不冬眠)
- P(一个月大|冬眠) P(零上|冬眠)
- P(一个月大|不冬眠) P(零上|不冬眠)
根据上面的表格我们得到
冬眠的情况下:
P(冬眠)=0.6
| feature1:温度 | 零上 | 零下 |
|---|---|---|
| 0 | 1 |
| feature2:年龄 | 一个月大 | 10天 |
|---|---|---|
| 0.67 | 0.33 |
不冬眠的情况:
P(冬眠)=0.4
| feature1:温度 | 零上 | 零下 |
|---|---|---|
| 1 | 0 |
| feature2:年龄 | 一个月大 | 10天 |
|---|---|---|
| 0.5 | 0.5 |
计算好我们所需的后
P ( 冬 眠 ∣ 一 个 月 大 , 零 上 ) = P ( 冬 眠 ) P ( 一 个 月 大 ∣ 冬 眠 ) P ( 零 上 ∣ 冬 眠 ) P ( 冬 眠 ) P ( 一 个 月 大 ∣ 冬 眠 ) P ( 零 上 ∣ 冬 眠 ) + P ( 不 冬 眠 ) P ( 一 个 月 大 ∣ 不 冬 眠 ) P ( 零 上 ∣ 不 冬 眠 ) = 0.5 × 0.67 × 0 0.5 × 0.67 × 0 + 0.5 × 0.5 × 1 = 0 \begin{aligned} P(冬眠|一个月大,零上)&=\frac{P(冬眠)P(一个月大|冬眠)P(零上|冬眠)}{P(冬眠)P(一个月大|冬眠)P(零上|冬眠)+P(不冬眠)P(一个月大|不冬眠)P(零上|不冬眠)}\\ &=\frac{0.5\times0.67\times0}{0.5\times0.67\times0+0.5\times0.5\times1}\\ &=0 \end{aligned} P(冬眠∣一个月大,零上)=P(冬眠)P(一个月大∣冬眠)P(零上∣冬眠)+P(不冬眠)P(一个月大∣不冬眠)P(零上∣不冬眠)P(冬眠)P(一个月大∣冬眠)P(零上∣冬眠)=0.5×0.67×0+0.5×0.5×10.5×0.67×0=0
所以,一个月大的瓢虫,在零上时冬眠的可能性为0
数据设计的不太好,但理解计算原理就好
朴素贝叶斯由于存在简化,所以很多时候表现不如决策树等算法
它的主场在文档分类,接下来主要理解朴素贝叶斯在文档分类中的应用
使用朴素贝叶斯进行文档分类
原理理解
在留言板上看到很多留言,我们希望利用朴素贝叶斯设计一个文档分类器,自动判断留言是属于侮辱性的还是非侮辱性的
我们先根据这个简单的例子,来手算一遍,理解朴素贝叶斯的过程
原始词条
我们看到留言板上存在“cute dog”“cute cute dog”“stupid”"stupid dog"这四条留言,这就是我们的原始词条
接下来我们根据词条中出现的单词选出词汇表
词汇表
| dog | cute | stupid |
|---|
统计词条,生成词向量
根据原始词条,统计每个单词在侮辱类和非侮辱类中是否出现,如果这个单词在句子中出现过就统计为1,没有出现过统计为0(注意:我们统计的是是否出现,而不是出现的次数)
| 序号 | dog | cute | stupid | 标签 |
|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 非侮辱类 |
| 2 | 1 | 1 | 0 | 非侮辱类 |
| 3 | 0 | 0 | 1 | 侮辱类 |
| 4 | 1 | 0 | 1 | 侮辱类 |
计算概率
为了方便计算结果,我们先统计下
P(非侮辱类)=0.5
非侮辱类的前提下:
| dog | cute | stupid |
|---|---|---|
| 2 4 \frac{2}{4} 42 | 2 4 \frac{2}{4} 42 | 0 |
P(侮辱类)=0.5
侮辱类的前提下:
| dog | cute | stupid |
|---|---|---|
| 1 3 \frac{1}{3} 31 | 0 | 2 3 \frac{2}{3} 32 |
计算结果
假如我们看到一个词条写着"cute and stupid",即特征为
| dog | cute | stupid |
|---|---|---|
| 0 | 1 | 1 |
(cute和stupid出现过,dog没有出现过)
若想判断这个词条是输入侮辱类还是非侮辱类,则需要分别计算 P ( 侮 辱 类 ∣ 特 征 ) P(侮辱类|特征) P(侮辱类∣特征)和 P ( 非 侮 辱 类 ∣ 特 征 ) P(非侮辱类|特征) P(非侮辱类∣特征),看哪个概率大,则最终结果属于这一类
以计算 P ( 侮 辱 类 ∣ 特 征 ) P(侮辱类|特征) P(侮辱类∣特征)为例:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ P(侮辱类|cute,stu…
出现了尴尬的事情,0/0
这是因为在连乘中,只要有一个概率为0,则乘积为0
除了这个问题以外,还会出现下溢出的问题
针对这两个问题,我们将进行小小的修改:
- 只要有一个概率为0,则乘积为0 -->拉普拉斯平滑
- 下溢出 --> 采用对数运算
具体的操作放在代码中解释
python代码
涉及到的全部函数:
- loadDataSet:创建实验数据集
- createVocabList:生成词汇表
- setOfWords2Vec:生成词向量
- get_trainMat:所有词条向量列表
- trainNB:朴素贝叶斯分类器训练函数
- classifyNB:朴素贝叶斯分类函数
- testingNB:朴素贝叶斯测试函数
函数loadDataSet:创建实验数据集
'''
函数名称:loadDataSet
功能:创建实验数据集
参数:无
返回:
postingList:切分好的样本词条
classVec:类标签向量
(1代表侮辱类,0代表非侮辱类)
modify:2019-05-27
'''
def loadDataSet():
dataSet = [
['my','dog','has','flea','problem','help','please'],
['maybe','not','take','him','to','dog','park','stupid'],
['my','dalmation','is','so','cute','I','love','him'],
['stop','posting','stupid','worthless','garbage'],
['mr','licks','ate','my','steak','how','to','stop','him'],
['quit','buying','worthless','dog','food','stupid']
]
classVec = [0,1,0,1,0,1]
return dataSet,classVec
dataSet,classVec = loadDataSet()
函数createVocabList:生成词汇表
'''
函数名称:createVocabList
函数功能:将切分的样本词条整理成词汇表(不重复)
参数说明:
dataSet
返回:
vocabList:不重复的词汇表
'''
def createVocabList(dataSet):
vocabSet=set()
for doc in dataSet:
vocabSet = vocabSet|set(doc)
vocabList = list(vocabSet)
return vocabList
vocabList = createVocabList(dataSet)
pd.Series(vocabList)
0 dog
1 I
2 steak
3 not
4 how
5 help
6 take
7 is
8 park
9 ate
10 flea
11 love
12 stop
13 stupid
14 worthless
15 him
16 licks
17 my
18 please
19 posting
20 mr
21 has
22 problem
23 quit
24 maybe
25 to
26 dalmation
27 buying
28 so
29 garbage
30 food
31 cute
dtype: object
可以看出,词汇表中一共有31个词汇
函数setOfWords2Vec:生成词向量
给出切分好的一句话,统计词汇表中的词汇是否在句子中出现过
'''
函数功能:根据vocabList词汇表,将inputSet向量化,向量的每个元素为1或0
参数说明:
vocabList:词汇表
inputSet:切分好的词条列表中的一条
返回:
returnVec:文档向量,词集模型
'''
def setOfWords2Vec(vocabList,inputSet):
returnVec=[0]*len(vocabList)
for word in vocabList:
if word in inputSet:
returnVec[vocabList.index(word)] = 1
return returnVec
#运行一下,看下函数的效果
Vec = setOfWords2Vec(vocabList,['my','dog','is','cute'])
pd.DataFrame(Vec,index = vocabList).T
| dog | I | steak | not | how | help | take | is | park | ate | ... | problem | quit | maybe | to | dalmation | buying | so | garbage | food | cute | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
1 rows × 32 columns
函数get_trainMat:所有词条向量列表
'''
函数名称:get_trainMat
函数功能:生成训练集向量列表
参数说明:
dataSet:切分好的样本词条
返回:
trainMat:所有词条向量组成的列表
'''
def get_trainMat(dataSet):
trainMat = []
vocabList = createVocabList(dataSet)
for sentence in dataSet:
trainMat.append(setOfWords2Vec(vocabList,sentence))
return trainMat
trainMat = get_trainMat(dataSet)
pd.DataFrame(trainMat,columns=vocabList)#方便查看才用的pd
| dog | I | steak | not | how | help | take | is | park | ate | ... | problem | quit | maybe | to | dalmation | buying | so | garbage | food | cute | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ... | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | ... | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ... | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
6 rows × 32 columns
函数trainNB:朴素贝叶斯分类器训练函数
'''
函数名称:trainNB
函数功能:朴素贝叶斯分类器训练函数
参数说明:
trainMat:训练文档矩阵
classVec:训练类别标签向量
返回:
pNAb:文档属于非侮辱类的概率
p1v:侮辱类的条件概率数组
p0v:非侮辱性的条件概率数组
pAb:文档属于侮辱类的概率
modify:2019-05-27
'''
def trainNB(trainMat,classVec):
pNAb = classVec.count(0)/len(classVec)
pAb = classVec.count(1)/len(classVec)
num_0 = 0
num_1 = 0
p0V=np.zeros(len(trainMat[0]))
p1V=np.zeros(len(trainMat[0]))
for i in range(len(trainMat)):
if classVec[i] == 1:
p1V += trainMat[i]
num_1 += sum(trainMat[i])
else:
p0V += trainMat[i]
num_0 += sum(trainMat[i])
p0V=p0V/num_0
p1V=p1V/num_1
return pNAb,pAb,p0V,p1V
pNAb,pAb,p0V,p1V=trainNB(trainMat,classVec)
pd.DataFrame(p0V,index = vocabList).T#方便查看结果
| dog | I | steak | not | how | help | take | is | park | ate | ... | problem | quit | maybe | to | dalmation | buying | so | garbage | food | cute | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.041667 | 0.041667 | 0.041667 | 0.0 | 0.041667 | 0.041667 | 0.0 | 0.041667 | 0.0 | 0.041667 | ... | 0.041667 | 0.0 | 0.0 | 0.041667 | 0.041667 | 0.0 | 0.041667 | 0.0 | 0.0 | 0.041667 |
1 rows × 32 columns
检验下我们的结果
比如’garbage’是一个偏侮辱性的词汇,我们分别查看下这个词在p0V和p1V中的概率,正常来说p1V>p0V
index = vocabList.index('garbage')
print(f'garbage 在p0V中的概率是{p0V[index]}')
print(f'garbage 在p1V中的概率是{p1V[index]}')
garbage 在p0V中的概率是0.0
garbage 在p1V中的概率是0.05263157894736842
函数classifyNB:朴素贝叶斯分类函数
这里会用到函数reduce
在python3中reduce放在了库 functools,所以在用reduce函数之前,需要先导入functools库
reduce中有两个参数,一个是函数f,一个是序列
reduce(f,[x1,x2,x3,x4])
reduce的用法
reduce中引入的这个函数f必须接收两个参数,reduce把f(x1,x2)的结果再与序列的下一个元素做累积计算,其效果就是:
reduce(f, [x1, x2, x3, x4]) = f(f(f(x1, x2), x3), x4)
强烈推荐看廖叔写的reduce的说明
https://www.liaoxuefeng.com/wiki/897692888725344/989703124920288
'''
函数名称:classifyNB
函数功能:朴素贝叶斯分类器分类函数
参数说明:
vec2Classify:待分类的词条数组
p0V:非侮辱类的条件概率数组
p1V:侮辱类的条件概率数组
pNAb:文档属于非侮辱类的概率
pAb:文档属于侮辱类的概率
返回:
0:属于非侮辱类
1:属于侮辱类
'''
def classifyNB(vec2Classify,p0V,p1V,pNAb,pAb):
from functools import reduce
p0 = pNAb*reduce(lambda x,y:x*y,p0V[np.array(vec2Classify)==1])
p1 = pAb*reduce(lambda x,y:x*y,p1V[np.array(vec2Classify)==1])
#因为分母是一样的,所以就偷懒,只算了分子
print(f'p0={p0}')
print(f'p1={p1}')
if p0>p1:
return 0
else:
return 1
classifyNB(setOfWords2Vec(vocabList,['garbage']),p0V,p1V,pNAb,pAb)
p0=0.0
p1=0.02631578947368421
1
函数testingNB:朴素贝叶斯测试函数
'''
函数说明:朴素贝叶斯测试函数
参数说明:
testVec:测试样本
返回:测试样本的类别
'''
def testingNB(testVec):
dataSet,classVec=loadDataSet()
trainMat = get_trainMat(dataSet)
pNAb,pAb,p0V,p1V = trainNB(trainMat,classVec)
vocabList = createVocabList(dataSet)
testV = setOfWords2Vec(vocabList,testVec)
if classifyNB(testV,p0V,p1V,pNAb,pAb):
print('侮辱类')
else:
print('非侮辱类')
#测试样本1
testingNB(['love','my','dalmation'])
p0=0.00010850694444444444
p1=0.0
非侮辱类
#测试样本2
testingNB(['cute','garbage'])
p0=0.0
p1=0.0
侮辱类
测试样本2体现出我们目前所码的朴素贝叶斯中存在的问题:
- 只要有一个概率为0,则乘积为0 -->拉普拉斯平滑
- 下溢出 --> 采用对数运算
拉普拉斯平滑
为了避免连乘时,只要有一个概率为0,整体乘积为0的问题,可以将所有词的出现都初始化为1,并将分母初始化为2,这种做法就叫做拉普拉斯平滑(Laplace Smoothing),又叫做加1平滑,是比较常见的平滑方法,它就是为了解决0概率问题
对于下溢出的问题,我们采用对数计算,通过求对数可以避免下溢出或者浮点数舍入导致的错误。
即
P ( 侮 辱 类 ∣ c u t e , s t u p i d ) = l o g ( P ( 侮 辱 类 ) P ˙ ( c u t e ∣ 侮 辱 类 ) P ( s t u p i d ∣ 侮 辱 类 ) P ( 侮 辱 类 ) P ˙ ( c u t e ∣ 侮 辱 类 ) P ( s t u p i d ∣ 侮 辱 类 ) + P ( 非 侮 辱 类 ) P ˙ ( c u t e ∣ 非 侮 辱 类 ) P ( s t u p i d ∣ 非 侮 辱 类 ) ) = l o g ( P ( 侮 辱 类 ) ) + l o g ( P ( c u t e ∣ 侮 辱 类 ) ) + l o g ( P ( s t u p i d ∣ 侮 辱 类 ) ) − l o g ( 分 母 ) \begin{aligned} P(侮辱类|cute,stupid)&=log(\frac{P(侮辱类)\dot P(cute|侮辱类) P(stupid|侮辱类)}{P(侮辱类)\dot P(cute|侮辱类) P(stupid|侮辱类)+P(非侮辱类)\dot P(cute|非侮辱类) P(stupid|非侮辱类)})\\ &=log(P(侮辱类))+log(P(cute|侮辱类))+log(P(stupid|侮辱类))-log(分母) \end{aligned} P(侮辱类∣cute,stupid)=log(P(侮辱类)P˙(cute∣侮辱类)P(stupid∣侮辱类)+P(非侮辱类)P˙(cute∣非侮辱类)P(stupid∣非侮辱类)P(侮辱类)P˙(cute∣侮辱类)P(stupid∣侮辱类))=log(P(侮辱类))+log(P(cute∣侮辱类))+log(P(stupid∣侮辱类))−log(分母)
原来的连乘运算就变成的连加运算
接下来对原有的朴素贝叶斯分类器对应的函数进行拉普拉斯平滑和对数运算
'''
函数名称:trainNB
函数功能:朴素贝叶斯分类器训练函数,进行拉普拉斯平滑的修改
参数说明:
trainMat:训练文档矩阵
classVec:训练类别标签向量
返回:
pNAb:文档属于非侮辱类的概率
p1v:侮辱类的条件概率数组
p0v:非侮辱性的条件概率数组
pAb:文档属于侮辱类的概率
modify:2019-05-27
'''
def trainNB(trainMat,classVec):
pNAb = classVec.count(0)/len(classVec)
pAb = classVec.count(1)/len(classVec)
# num_0 = 0
# num_1 = 0
# p0V=np.zeros(len(trainMat[0]))
# p1V=np.zeros(len(trainMat[0]))
num_0 = 2 #分母初始化为2
num_1 = 2 #分母初始化为2
p0V=np.ones(len(trainMat[0])) #词条出现初始化为1
p1V=np.ones(len(trainMat[0])) #词条出现初始化为1
for i in range(len(trainMat)):
if classVec[i] == 1:
p1V += trainMat[i]
num_1 += sum(trainMat[i])
else:
p0V += trainMat[i]
num_0 += sum(trainMat[i])
# p0V=p0V/num_0
# p1V=p1V/num_1
p0V=np.log(p0V/num_0)
p1V=np.log(p1V/num_1)
return pNAb,pAb,p0V,p1V
'''
函数名称:classifyNB
函数功能:朴素贝叶斯分类器分类函数,进行对数运算的修改
参数说明:
vec2Classify:待分类的词条数组
p0V:非侮辱类的条件概率数组
p1V:侮辱类的条件概率数组
pNAb:文档属于非侮辱类的概率
pAb:文档属于侮辱类的概率
返回:
0:属于非侮辱类
1:属于侮辱类
'''
def classifyNB(vec2Classify,p0V,p1V,pNAb,pAb):
p0 = np.log(pNAb)+sum(np.array(vec2Classify)*p0V)
p1 = np.log(pAb)+sum(np.array(vec2Classify)*p1V)
#因为分母是一样的,所以就偷懒,只算了分子
print(f'p0={p0}')
print(f'p1={p1}')
if p0>p1:
return 0
else:
return 1
#测试样本2
testingNB(['cute','garbage'])
p0=-6.516193076042964
p1=-6.089044875446846
侮辱类
修改后,就基本解决上述问题啦
文档词袋模型
之前我们将每个词的出现与否作为一个特征,这可以被描述为词集模型(set-of-words model)
如果一个词在文档中出现不止一次,这可能意味着包含该词是否出现在文档中所不能表达的某种信息,这种方法被称为词袋模型(bag-of-words model)。
在词袋中,每个单词可以出现多次,而在词集中,每个词只能出现一次。为了适应词袋模型,需要对函数setOfWords2Vec()稍加修改,修改后的函数称为bagOfWords2Vec()
只需要每遇到一个单词的时候,增加词向量中的对应值,而不是只将对应的数值设为1
def bagOfWords2Vec(vocabList,inputSet):
returnVec=[0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] += 1
return returnVec
下一个文档将涉及更加完整的朴素贝斯叶分类算法的实例,毕竟是实际遇到的案例是文本内容,而非已经被切好的字符串列表。
以及sklearn中关于朴素贝叶斯的部分
更完整的实例:过滤垃圾邮件
在文件夹email中,存有已经分类好的邮件。相对于之前的案例,这次我们需要先对文本进行切分,并将所有所有数据存储在docList中,所有标签存储在classList中
函数:textParse文本切分
'''
函数名称:textParse
函数说明:接受一个大字符串,并将其解析为字符串列表
参数:bigString
返回:字符串列表
modify:2019-05-28
'''
def textParse(bigString):
import re #使用python中正则表达式
listOfTokens = re.split(r'\W+',bigString) #+表示重复多次,任何非大小写字母和数字
return [i.lower() for i in listOfTokens if len(i)>2]#删除掉短于2个字符的单词
函数:getData获得全部数据集
'''
函数名称:getData
函数说明:从email文件夹中获得全部数据集和标签
参数:None
返回:
docList-全部文本数据
classList-全部标签
nameList-文件名称,方便查找具体的文件
'''
def getData():
from os import listdir
docList=[]
classList=[]
nameList=[]
classname = listdir('email')
for i in classname:
dirlist = listdir('email/%s'%i)
for a in dirlist:
with open('email/%s/%s'%(i,a),errors='ignore') as f:
docList.append(textParse(f.read()))
classList.append(i)
nameList.append(f'{i}-{a}')
return docList,nameList,classList
docList,nameList,classList = getData()
content = pd.concat([pd.DataFrame(classList,columns=['class']),pd.DataFrame(docList)],axis=1)
content.index=nameList
content.head(5) #方便查看下每个文件的分词
| class | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 | 202 | 203 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| spam-15.txt | spam | you | have | everything | gain | incredib1e | gains | length | inches | yourpenis | ... | None | None | None | None | None | None | None | None | None | None |
| spam-14.txt | spam | buyviagra | 25mg | 50mg | 100mg | brandviagra | femaleviagra | from | per | pill | ... | None | None | None | None | None | None | None | None | None | None |
| spam-16.txt | spam | you | have | everything | gain | incredib1e | gains | length | inches | yourpenis | ... | None | None | None | None | None | None | None | None | None | None |
| spam-17.txt | spam | home | based | business | opportunity | knocking | your | door | dont | rude | ... | None | None | None | None | None | None | None | None | None | None |
| spam-13.txt | spam | ordercializviagra | online | save | 0nline | pharmacy | noprescription | required | buy | canadian | ... | None | None | None | None | None | None | None | None | None | None |
5 rows × 205 columns
函数:划分数据集和测试集
'''
函数名称:split_train_test
函数说明:随机划分数据集和测试集
参数:
N-数据集个数
rate-划分比例
返回:trainIndex-训练集的序号列表
testIndex-测试集的序号列表
'''
def split_train_test(N,rate=0.8):
import random
indexList = list(range(N))
random.shuffle(indexList)
trainIndex = indexList[:int(N*rate)]
testIndex = indexList[int(N*rate):]
return trainIndex,testIndex
#验证一下刚刚写的函数
trainIndex,testIndex=split_train_test(50)
testIndex
[11, 36, 24, 40, 14, 32, 16, 19, 43, 30]
函数:训练朴素贝叶斯分类器
有了前面的3个函数,我们接下来就可以使用之前已经写好的朴素贝叶斯函数,进行邮件的分类
'''
函数名称:spamText
函数说明:训练朴素贝叶斯
参数:
返回:
modify:2019-05-28
author:stacy
'''
def spamText():
docList,nameList,classList = getData() #获得数据集
trainIndex,testIndex = split_train_test(len(docList)) #获得训练样本
classList=np.array(classList)
classLabel=np.zeros(classList.shape)
classLabel[classList=='spam']= 1
classLabel[classList=='ham']= 0
Xtrain = list(np.array(docList)[trainIndex])
Ytrain = list(classLabel[trainIndex])
Xtest = list(np.array(docList)[testIndex])
Ytest = list(classLabel[testIndex])
vocabList = createVocabList(Xtrain) #获得词集
trainMat = get_trainMat(Xtrain)
pNAb,pAb,p0V,p1V = trainNB(trainMat,Ytrain)
res = []
for i in Xtest:
a = setOfWords2Vec(vocabList,i)
if classifyNB(a,p0V,p1V,pNAb,pAb):
res.append(1)
else:
res.append(0)
print((np.array(res)!=np.array(Ytest)).mean())
spamText()
p0=-56.0404856438534
p1=-61.69417280033571
p0=-46.571380928877744
p1=-47.592936081468174
p0=-71.3416264916052
p1=-77.83176446646347
p0=-147.39616219436843
p1=-122.3205105193053
p0=-185.76362389676441
p1=-137.8874060021816
p0=-155.97062564916678
p1=-133.9414156447548
p0=-59.38387270998675
p1=-67.79224708250196
p0=-185.76362389676441
p1=-137.8874060021816
p0=-38.06279130893568
p1=-43.66391549967146
p0=-185.76362389676441
p1=-137.8874060021816
0.0
错误率还是非常低的
下一篇文章将介绍sklearn中朴素贝叶斯的使用和更多的案例