机器学习之聚类

一、聚类基本介绍

Clustering

1. 将数据集在某些方面相似的数据成员进行分类组织的过程
2. 无监督学习算法

聚类前需要进行数据标准化！

---

二、性能度量

我们希望同一簇的样本应该尽可能彼此相似，不同簇的样本尽可能不同。

详细内容见西瓜书p198-p199

1. 外部指标

将聚类结果与某个“参考模型”进行比较。

1.1 Jaccard系数

1.2 FM指数

1.3 Rand指数

2. 内部指标

直接考察聚类结果而不利用任何参考模型。

2.1 Davies-Bouldin Index (DBI)

2.2 Dumm Index (DI)

---

三、距离计算

1. 针对有序属性

例如“1”和“2”比较近，“3”比较远

2. 针对无序属性

例如{飞机，火车，轮船}这样的离散属性，不能直接在属性值上计算距离，一般采用VDM进行距离的计算

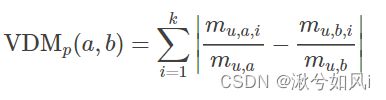
m_u,a表示在属性u上取值为a的样本数
m_u,a,i表示第i个样本簇中在属性u上取值为a的样本数

3. 针对混合属性

假设有n_c个有序属性，n-n_c个无序属性

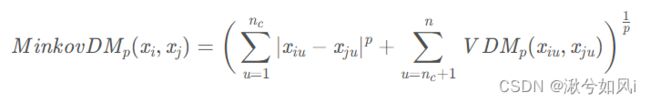
若不同属性的重要性不同时，可使用加权距离

---

四、原型聚类

K-均值聚类算法

K-means Clustering：给定一个数据点集合和需要的聚类数目k(用户指定)，根据某个距离函数反复地把数据分入k个聚类中。

1. 随机选取k个数据点作为初始聚类中心（某聚类中所有数据点的均值）
2. 计算每个数据点与各个种子聚类中心之间的距离，把每个数据点分配给距离它最近的聚类中心，形成一个聚类
3. 待所有数据点均被分配后，每个聚类根据当前聚类中的数据点，重新计算出新的聚类中心
4. 以上步骤不断重复，直到没有(或最小数目)数据点被重新分配给不同的聚类/没有(或最小数目)聚类中心再发生变化/误差平方和(SSE)局部最小

具体过程配上web数据挖掘P90图4.3

---

python实现

import numpy as np

def loadDataSet(filename):
    dataMat = []
    f = open(filename)
    for line in f.readlines():
        curLine = line.strip().split()
        fltLine = list(map(float, curLine))   # 将所有元素都映射成float()
        dataMat.append(fltLine)
    return dataMat


def distEclud(vecA, vecB):
    return np.sqrt(np.sum(np.power(vecA-vecB, 2)))


# 构建一个包含k个随机质心的集合
def randCent(dataSet, k):
    n = np.shape(dataSet)[1]
    centroids = np.mat(np.zeros((k, n)))

    for j in range(n):
        minJ = np.min(dataSet[:, j])
        rangeJ = float(np.max(dataSet[:, j]) - minJ)
        centroids[:, j] = minJ + rangeJ * np.random.rand(k, 1)
    return centroids


"""
创建k个点作为起始质心(随机选择)
当任意一个点的簇分配结果发生改变时
    对数据集中的每个数据点
        对每个质心
            计算质心与数据点的距离
        将数据点分配到距离其最近的簇
    对每一个簇，计算簇中所有点的均值并将均值作为质心
"""

def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    m = np.shape(dataSet)[0]  # 有几个样本
    clusterAssment = np.mat(np.zeros((m, 2)))     # 簇分配及结果矩阵 列1:簇索引值 列2:存储误差
    centroids = createCent(dataSet, k)
    clusterChanged = True  # 循环条件
    while clusterChanged:
        clusterChanged = False

        for i in range(m):  # 对每个样本点
            minDist = np.inf  # 设为无穷大
            minIndex = -1

            for j in range(k):  # 对于每个质心
                distance = distMeas(centroids[j, :], dataSet[i, :])   # 计算当前点与质心的距离
                if distance < minDist:  # 若当前距离小于之前的最小距离
                    minIndex = j        # 更新簇索引
                    minDist = distance  # 更新最小距离

            if clusterAssment[i, 0] != minIndex:    # 若当前样本点簇索引改变
                clusterChanged = True               # 则需要进行下一轮循环
                clusterAssment[i, 0] = minIndex     # 更新数据
            clusterAssment[i, 1] = minDist**2       # 计算SSE误差平方和

        for cent in range(k):  # 对每一个簇，更新质心
            ptsInClust = dataSet[np.nonzero(clusterAssment[:, 0].A == cent)[0]]  # 获取在这一簇中的所有样本点
            centroids[cent, :] = np.mean(ptsInClust, axis=0)    # 列的均值，沿着行

    return centroids, clusterAssment


if __name__ == '__main__':
    dataMat = np.mat(loadDataSet('testSet.txt'))
    myCentroids, clustAssing = kMeans(dataMat, 4)
    print(myCentroids, clustAssing)
    

• k是用户自定的参数，难以准确确定。
• 生成簇可能不是最优簇，因为最开始的质心是随机出来的，只能保证从这个起点出发得到的距离最小值（局部最小值），而无法保证是全局的距离最小值。
• 可以采用SSE(Sum of Squared Error，误差平方和)来度量聚类的效果。SSE值越小表示数据点越接近于它们的质心，聚类效果也越好。因为对误差取了平方，因此更重视那些远离中心的点。
• 一种方法是可以将具有最大SSE的簇划分成2个簇，然后为了保持簇数不变，再将某两个离得近的簇合并。

一种改进算法二分K-均值算法略

---

sklearn实现

import matplotlib.pyplot as plt
from sklearn.datasets._samples_generator import make_blobs

X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)  
# 生成测试集
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.show()

# ---------------------KMeans--------------------
from sklearn.cluster import KMeans

m_kmeans = KMeans(n_clusters=4)  
m_kmeans.fit(X)
y_pred = m_kmeans.predict(X)

# ---------------------KMeans--------------------

from sklearn import metrics

def draw(m_kmeans,X,y_pred,n_clusters):
    centers = m_kmeans.cluster_centers_
    print(centers)
    plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=50, cmap='viridis')
    # 中心点（质心）用红色标出
    plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.5)
    print("Calinski-Harabasz score：%lf" % metrics.calinski_harabasz_score(X, y_pred))
    plt.title("K-Means (clusters = %d)" % n_clusters, fontsize=20)
    plt.show()

draw(m_kmeans,X,y_pred,4)	# 画出聚类结果

KMeans()参数及属性

    KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300,
            tol=0.0001, precompute_distances='auto', verbose=0, 
            random_state=None, copy_x=True, n_jobs=1, algorithm='auto')

1. n_clusters: 聚类个数
2. max_iter： 最大迭代数
3. n_init： 用不同的质心初始化值运行算法的次数
4. init： 初始化质心的方法
5. precompute_distances：预计算距离
6. tol：关于收敛的参数
7. algorithm：“auto”, “full” or “elkan” ，”full”就是我们传统的K-Means算法，“elkan”elkan K-Means算法。默认的”auto”则会根据数据值是否是稀疏的，来决定如何选择”full”和“elkan”,稠密的选 “elkan”，否则就是”full”

• cluster_centers_：质心坐标
• labels_: 每个点的分类列表[0,1,0,1,2,3]
• inertia_：每个点到其簇的质心的距离之和

---

优点

简洁、效率高，容易理解也容易实现。

缺点

1. 算法只能应用于均值能够被定义的数据集中
2. 用户需要事先指定聚类数目k
3. 算法对于异常值十分敏感
4. 算法对初始聚类中心的选取十分敏感
5. 不适合用于那些形状不是超维椭圆体（或超维球体）的聚类

---

五、层次聚类

1. 自上而下聚类

从树状图的最底层开始，每一次通过合并最相似(距离最近)的聚类来形成上一层中的聚类。整个过程当全部数据点都合并到一个聚类(根节点聚类)中时停止。

2. 自下而上聚类

从一个包含全部数据点的聚类(根)开始。然后把根节点聚类分裂成一些子聚类。每个子聚类再递归地继续往下分裂直到每个聚类中只包含一个数据点。

计算两个聚类之间的距离

1. 单链接方法：两个聚类中距离最近的两个数据点之间的距离。对噪音敏感，可能发生连锁反应，时间复杂度O(n²)
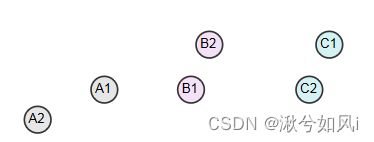
2. 全链接方法：两个聚类中所有数据点之间距离的最大值。即每次合并最远元素具有最短距离的聚类。（因为distance(B1, C1) < distance(A2, B2)，所以B类和C类合并在一起）
3. 平均链接方法：一个聚类的所有数据点到另一个类的所有数据点的平均距离。

优点

能够使用任何形式的距离或相似度函数，层次结构更能提供一些细节

缺点

时空复杂度高，对异常值十分敏感

---

六、密度聚类

1. DBSCAN算法

---

问题

1. 怎样计算例如{飞机，火车，轮船}这样的无序属性之间的距离？VDM(Value Difference)和简单匹配距离(Simple Matching Distance)有什么区别，各自的应用场景是什么？