进制转化（二进制，八进制，十进制，十六进制）详细教程

上一章我们提及到了进制转化，今天我们来详细的来讲解一下。

我们先说十进制吧，就是我们平常所说的0,1,2,3,4,5,6,7,8,9,我们计算加法的时候都是逢十进一

就是我们计算的时候，一到十就立马清零了并加到下一位。所以范围是0~9.

二进制也是如此，就是逢二进一，只有0，1这两个数字，一到二就立马清零并加到下一位。

既范围是0~1。

八进制，十六进制同样的道理，但是十六进制需要特别说明一下：十六进制中，从10开始

（包括10），一直到15，分别用ABCDEF表示，比如12，用C表示。

了解基本概念，那我们来讲讲进制转化吧。

---

目录

二进制转十进制

十进制转二进制

八进制转十进制

十六进制转十进制

 二进制转八进制、二进制转十六进制、八进制转二进制、十六进制转二进制、十六进制转八进制、八进制转十六进制

 十进制转八进制

十进制转十六进制

---

二进制转十进制

这不得不说一下权重，我就简单抽象的描述一下，比如M进制，它的第N位的权重是.

来个例子：

十进制的169，个位的权重就是既=1，十位的权重是，百位的权重是，我们把每一位上的数乘以各自的权重，既9*+6*+1*=169.这样就基本讲清了。

二进制亦是同样的道理。

exp1.

比如1011

右边从左数第一个1权重是，第二个1是权重是，......以此类推。

所以1011转化为十进制就是

1*+1*+0*+1*=11.

所以1011的十进制是11.

exp2.

我们再来一个例子巩固一下

把1110

还是各个位乘以各自的权重

0* + 1* + 1* + 1* =14.

所以1110的十进制是14.

十进制转二进制

整数部分：

这个就比较难点了，方法：

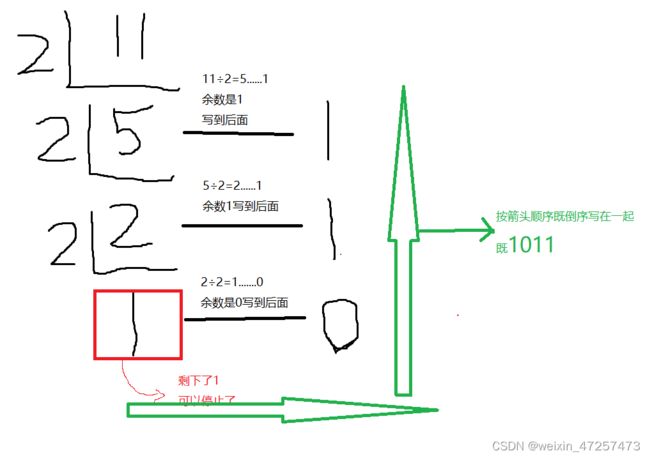
（一）.就是每次让十进制的数除以2，然后把每次的余数写出来，最后除到剩下1停止，然后倒序写出来。

具体过程看如下：

我们把十进制的11转化为二进制

 是不是和上面的二进制1011转化为十进制一样？

这就是一种最经典的转化方式。

（二）.还有一种不正规但常用的方式。我们想象当数字特别大的时候，比如我们想把2099这样的数字转化为二进制，你去一个2一个2除吧，会很长的也很费时间。

我们知到从右向左每一位都是前一位权重的2倍，我们说4的二进制是多少，我们一想，二进制中第一位的权重是1，第二位的权重是2，第三位的权重是4。诶，既然第三位的权重是4，那我们直接在第三位写一个1，后面的都是0，这样表示的不正好是4吗

这样我们明白了，4的二进制是100。8的二进制也是同样的道理，二进制中第4位的权重是8，所以我们只需要让第4位是1，就是1000，就是8的二进制了。

那如果是9呢？既不是第4位也不是第5位，那怎么办呢？我们可以拆分一下

9=8+1

其中8是二进制的第四位，1是二进制的第一位，所以我们只需要在二进制中的第四位和第一位填上个1就可以了，其他位全是0既1001。

知道了这样的原理，我们就可以更快解决高位数的二进制了。

这里需要我们熟练掌握2的几次方分别是多少，比如2的9次方，你须迅速反应出是512，记住2^10以内的就够了。

再回到刚才的例子，2099的二进制，我们知道2^10=1024，所以2^11=2048.

我们把2099拆分为下面的数（注意必须是2的倍数）

我们先找最接近2099的数，就是2048，2^11，在二进制中是第12位。

找到了之后，我们再拆分剩下的数。

2099-2048=51.

我们再找最接近51的数，发现是32,2^5，在二进制中是第6位，32的下一个位数的权重是64，就太大了。

再分剩下的数

51-32=19

我们再找最接近19的数，发现是16，2^4，在二进制是第5位。

再分剩下的数

19-16=3

同样的道理

最接近3的数是2，二进制第二位。

剩下1就不用再分了，二进制第一位。

我们从最高位依次写下，得到

100000110011

我们可以验证一下：

1*+1*+1*+1*+1*=1+2+16+32+2048=2099.

结果正确。

以上我们说的是整数部分，那如果十进制有小数呢？

小数部分

比如我们要把10.25转化为二进制。

整数部分10我们按照上面的方法转化就行。

方法是把小数部分不断乘以2，将积的整数部分取出，继续乘以2，依次进行，积中的小数部分为零，或者达到所要求的精度为止。

我们举例说明。

exp1：

10.25

10转化为二进制是1010

0.25我们先乘以2得到0.5，取整数部分0作为小数的第一位。

再继续乘以2,0.5乘以2得到1.0，整数部分为1作为小数的第二位，此时由于小数部分已经为0，停止相乘。

所以小数部分是01

我们结合起来，所以是1010.01.

exp2：

我们把3.625转化为二进制。

先转换整数部分3为二进制11。

0.625*2=1.25 取出整数1，作为小数第一位

1.25取出1还剩0.25,0.25*2=0.5，取出整数0，作为小数第二位

0.5*2=1.0，取出整数1,作为小数第三位，由于小数部分为0，循环停止。

所以3.625的二进制是11.101

exp3：

对于0.11这种不可能乘到尽头的数，我们按照题目要求取适当的精度即可。

八进制转十进制

这和上面的二进制转十进制是完全一样的道理，只不过权重发生了改变。我在此举几个例子来说明即可。

把八进制的130转化为10进制。

从右往左数第一位所占的权重是，第二位是，第三位是。

所以我们用权重乘以各自的位数。

既0*+3*+1*=64+24=88。

十六进制转十进制

也是同理，只是权重发生了变化。

举一个例子来说明即可。

把150这个十六进制的数转化为10进制。

从右往左数第一位权重数，第二位是，第三位是。

所以我们用权重乘以各自的位数

0*+5*+1*=80+256=336.

 二进制转八进制、二进制转十六进制、八进制转二进制、十六进制转二进制、十六进制转八进制、八进制转十六进制

之所以放在一起说，因为原理方法基本一样。

1.二进制转八进制

先说方法，方法是小数点左边（整数部分）从右向左把二进制的每三位分成一组，不足位补0.然后在按各自的权重相加，小数点右边（小数部分）从左向右把二进制的每三位分成一组，不足的位补0，最后在按各自的权重相加。

我们来看图：

比如我们把1001111001这个二进制数转化为八进制

怎么样，是不是很简单呢？

下面我们来举一个小数部分的例子。

我们把二进制的10110011.11001转化为八进制。

利用这种办法可以很高效的进行进制转化。

 2.八进制转二进制

其实是上面那种方法的逆过程

把八进制的每一位数字分成三个二进制数字，最后组合起来既是结果。

我们来看例子。

我们要把八进制的752转化为二进制。

先看2，要把2转化为三位数的二进制，对应的是010.

5对应的是101,7对应的是111.

所以合在一起是111101010.

我用图片展示一下。

 

 3.二进制转十六进制

这个和二进制转八进制的那个方法很相似。二进制转八进制是三位一组，二进制转十六进制则是四位为一组，位数不足补0.

（方法是小数点左边（整数部分）从右向左把二进制的每四位分成一组，不足位补0.然后在按各自的权重相加，小数点右边（小数部分）从左向右把二进制的每四位分成一组，不足的位补0，最后在按各自的权重相加。）

直接上例子。

把二进制的1001111010100转化为16进制

上图：

是不是和二进制转八进制很像？小数部分也是同样的道理，可以参考上面的二进制转八进制那一小节的小数部分的转化，道理完全一样。

4.十六进制转二进制

也是上面方法的逆过程。

既把十六进制的每一位数字分成四个二进制数字，最后组合起来既是结果

也是直接上例子

我们把16a1这个十六进制数字转化为二进制（a是十六进制中的10，上面说了哦）

上图：

这样，十六进制转二进制就全部说完了。

5.八进制转十六进制

总体思路是：1.八进制转二进制。2.二进制再转十六进制。

这些进制转化我们上面都说了，所以现在说起来会很简单。

还是先上例子：

把八进制的167转化为十六进制。

我们按以下步骤进行：

1.1   八进制转二进制

此时八进制的167转化为二进制是1110111。

1.2   二进制转十六进制

我们把刚才的二进制利用上面的方法转化为十六进制

这样就转化完成啦！

6.十六进制转八进制

和刚才的方法相似：

1.先把十六进制转化为二进制。2.再把二进制转化为八进制。

先上例子：

我们把十六进制的95转化为八进制

1.1   我们先把十六进制的95转化为二进制

如下图：

1.2    将二进制的10010101转化为八进制

上图：

这样十六进制转八进制我们就说完了。

 十进制转八进制

 这个有两种办法：

1.现将十进制转化为二进制，进而将二进制转化为八进制，2.直接法，除8取余

我们先来看第一种方法

 我们要把十进制的169转化为八进制。

1.1先把十进制转化为二进制：

按上面的讲的一个简洁方法，就是拆分，当然你除2取余也可以都一样

169 = 128 + 32 + 8 + 1 

转到二进制：10101001

1.2二进制转八进制

按上面的，取三合一

010   101      001

  2        5         1

所以十进制的169转化为八进制是251.

接下来看第二种方法：

和上面讲的那个10进制转二进制的那个除二取余的方法基本相似，这个只不过是除以8

看下图：

这样我们十进制转八进制也完成了。

十进制转十六进制

和上面的又是几乎一样的方法，也是两种：

1.现将十进制转化为二进制，再将二进制转化为十六进制。2.除16取余法

同样先来看第一种方法：

我们把十进制的617转化为十六进制

1.1现将十进制的617转化为二进制，我还是采用上面所讲的拆分的方法

617 = 512 + 64 + 32 + 8 + 1

既1001101001。

1.2再将二进制的1001101001转化为十六进制

取四合一（上面讲的）

0010     0110     1001

   2            6          9

 所以十进制的617转化为十六进制就是269.

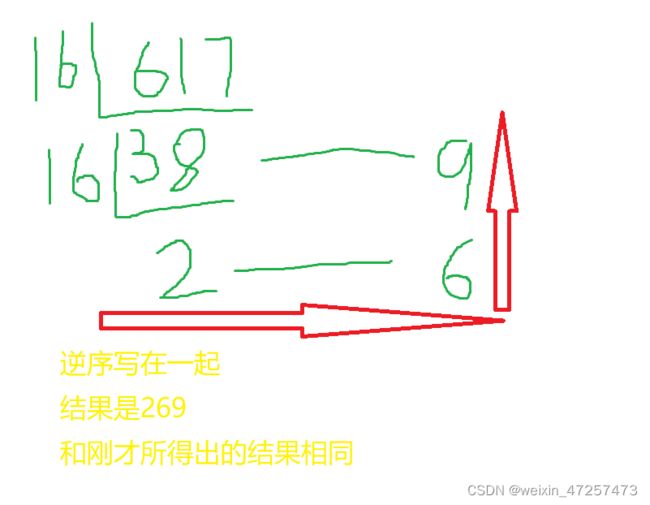
再来看第二种方法，也是直接上图看过程：

这样，十进制转十六进制的教程也就说完了。

好了，至此，各个进制转化的教程已经全部讲完，其中可能会有一些细节的疏漏，如果有不懂的地方或者需要改进的地方，欢迎评论区留言或私信我哦。