数据挖掘分析考试笔记
数据挖掘分析考试笔记
文章目录
- 数据挖掘分析考试笔记
-
- 英译汉
- 第一章 绪论
- 第二章 知识发现过程与应用结构
- 第三章 关联规则挖掘
-
- Apriori算法
- close算法
- FP-tree
- 第四章 分类
-
- 分类两个步骤
- 基于距离的类标识搜素算法
- KNN
- 决策树 ID3
- 贝叶斯分类
- EM算法(Expectation-Maximization Algorithm)
- 混淆矩阵
- 第五章 聚类
-
- 距离与相似性的度量
- K-Means算法
- PAM(Partitioning Around Medoid)围绕中心点的划分
- 层次聚类方法
-
- AGNES算法
- DIANA算法
- DBSCAN
- 第六章 时间序列和序列模式挖掘
- 第七章 PageRank
英译汉
- KDD, Knowledge Discovery in Database 知识发现
- supervised learning 监督学习
- Batesian Classification 贝叶斯分类
- Agglomeration 凝聚
- Division 分裂
- information retrieval 信息检索
- Knowledge Engineering 知识工程
- OLTP(On-Line Transaction Processing) 联机事务处理
- OLAP(On-Line Analytic Processing) 联机分析处理
- Decision Support 决策支持
- Distributed Database 分布式数据库
- Lattice of Closed Itemset 闭合项目集格空间
- Parallel Association Rule Mining 并行关联规则挖掘
- Quantities Association Rule Mining数量关联规则挖掘
- KNN(k-Nearest Neighbors) k最临近
- decision tree 决策树
- overfitting 过拟合
- Iterative Dichotomization
- Expectation-Maximization
- PAM(partitioning around medoid) 围绕中心点的划分
- DBSCAN(Density-Based Spatial Clustering of Applications with Noise) 基于密度的噪声应用空间聚类
- Partitioning method 划分方法
- Hierarchical method 层次方法
- Grid-based method 基于网格的方法
- STING(Statistical Information Grid-based Method) 基于网格的统计信息方法
- Time Series 时间序列
- AR(Auto Regressive) 自回归
- Sequential Mining 序列挖掘
- Offset Translation 偏移变换
- Subsequence Ordering 子序列排序
- Crawler 爬虫
- Look up Page 查找页
- posterior probability 后验概率
- prior probability 先验概率
第一章 绪论
-
数据挖掘概念
数据挖掘是从大量的、不完全的、模糊的、有噪声的、随机的数据集中识别有效的、新颖的、潜在可用的信息,以及最终可理解的模式的非平凡过程。
-
数据挖掘与知识发现的关联性
-
KDD是数据挖掘的一个特例
-
数据挖掘是KDD过程的一个步骤
数据挖掘是在KDD中通过特定的算法在可接受的计算效率限制内生成特定模式的一个步骤。
-
含义相同
-
第二章 知识发现过程与应用结构
-
KDD的阶段划分、功能、任务
-
问题定义
和领域专家及最终用户紧密协作,一方面了解相关领域的有关情况、熟悉背景知识、弄清用户要求、确定挖掘目标等要求,另一方面通过对各种学习算法的对比而确定可用的学习算法
-
数据采集
选取相应的源数据库,并根据要求从数据库中提取相关的数据
-
数据预处理
对前一阶段的数据进行再加工,确定数据的完整性和一致性
-
数据挖掘
运用选定的数据挖掘算法,从数据中提取出用户所需要的知识
-
模式评估
将KDD系统发现的知识以用户能理解的方式呈现,并且根据需求对知识进行评价,如果发现的知识和用户所需要的不一致,则重复以上阶段以最终获得可用知识
-
第三章 关联规则挖掘
频繁项目集:大于或等于MinSupport的项目集合的非空子集,称为频繁项目集
强关联规则:事务数据库在项目集合上满足最小支持度和最小置信度的关联规则成为强关联规则
关联规则挖掘问题可以划分成两个子问题:
-
发现关联规则
**通过用户给定的最小支持度,寻找所有的频繁项目集,即满足Support不小于MinSupport的所有项目集合
-
生成关联规则
通过用户给定的最小置信度,在每个最大频繁项目集中,寻找Confidence不小于MinConfidence的关联规则
Apriori算法
原理:频繁项目集的所有非空子集都是频繁项目集,非频繁项目集的所有超集都是非频繁项目集
Apriori(发现频繁项目集)
输入:项目集合D,最小支持度minsup_count
输出:频繁项目集L
L 1 L_1 L1 = {lager 1-itemsets};
FOR(k = 2; L k − 1 ≠ Φ L_{k-1} \neq \Phi Lk−1=Φ; k++) DO BEGIN
C k C_k Ck = apriori_gen( L k − 1 L_{k-1} Lk−1);
FOR all trancation t ∈ \in ∈D DO BEGIN
C t C_t Ct = subset( C k C_k Ck, t);
FOR all condiation c ∈ \in ∈ C t C_t Ct DO c.count++;
END
L k L_k Lk = {c ∈ \in ∈ C k C_k Ck | c.count ≥ \geq ≥minsup_count}
L = ∪ \cup ∪ L k L_k Lk
apriori_gen(候选集生成)
输入:(k-1)-频繁项目集 L k − 1 L_{k-1} Lk−1
输出:k-候选项目集 C k C_k Ck
FOR all itemset q ∈ \in ∈ L k − 1 L_{k-1} Lk−1 DO
FOR all itemset p ∈ \in ∈ L k − 1 L_{k-1} Lk−1 DO
IF q.item1 = p.item1, q.item1 = p.item ⋯ \cdots ⋯ q.itemk-2 = p.itemk-2, q.itemk-1 < p.itemk-1
THEN BEGIN
c = q ∞ \infty ∞p
IF has_inference_subset(c, L k − 1 L_{k-1} Lk−1)
delete c
ELSE IF
add c to C k C_k Ck
END
Return C k C_k Ck
has_inference_subset(判断候选集元素)
输入:候选集c,(k-1)-频繁项目集 L k − 1 L_{k-1} Lk−1
输出: L k − 1 L_{k-1} Lk−1中是否含有c的全部(k-1)-子集的布尔判断(c是否被删除的布尔判断)
FOR all (k-1)-itemset of c DO BEGIN
IF s ∉ \notin ∈/ L k − 1 L_{k-1} Lk−1 THEN Return TRUN
Return FALSE
close算法
原理:一个频繁闭合项目集的闭合子集一定是频繁的,一个非频繁闭合项目集的闭合超集一定是非频繁的。
计算:见colse算法PPT
FP-tree
FP-tree算法主要由两个步骤完成:
- 利用事务数据库中的数据构造FP-tree
- 从FP-tree中挖掘频繁模式
只需两次数据库的扫描:
- 对所有1-项目集的频度排序
- 将数据库信息转变成紧缩内存结构
算法例子:
| TID | Itemset |
|---|---|
| 1 | A,B,C,D |
| 2 | B,C,E |
| 3 | A,B,C,E |
| 4 | B,D,E |
| 5 | A,B,C,D |
扫描一次数据库,得到频数排序
| item | count |
|---|---|
| B | 5 |
| C | 4 |
| A | 3 |
| D | 3 |
| E | 3 |
根据频数对事务数据库重新排列
| TID | Itemset |
|---|---|
| 1 | B,C,A,D |
| 2 | B,C,E |
| 3 | B,C,A,E |
| 4 | B,D,E |
| 5 | B,C,A,D |
构造FP-tree

寻找路径生成频繁项目集
| item | 条件模式基 | 条件FP-tree | 产生的频繁模式 |
|---|---|---|---|
| A | {(BC:3)} | BC:3 | AB,AC,ABC |
| B | NULL | NULL | NULL |
| C | {(B:4)} | B:4 | BC |
| D | {(BCA:2),(B,1)} | BCA:2 | AD,BD,CD,ABD,BCD,ACD,ABCD |
| E | {(BD,1),(BC,2),(BCA,1)} | BC:2 | BCE |
最大频繁项目集{BCE, ABCD}
第四章 分类
分类两个步骤
-
建立一个模型,描述预定的数据类集或概念集
-
使用模型进行分类。首先评估模型的预测准确率,如果准确率可以接受,那么就用他来对类标号未知的元组进行分类
基于距离的类标识搜素算法
输入:每个类的中心 C 1 C_1 C1, C 2 C_2 C2, C 3 C_3 C3… C m C_m Cm,待分类元组t
输出:t的类别c
dist = ∞ \infty ∞;
FOR i=1 to m DO
IF dist( C 1 C_1 C1, t) < dist THEN BEGIN
dist = dist( C 1 C_1 C1, t);
c=i;
END
flag t with c
KNN
思想:假定每个类包含多个训练数据,且每个训练数据都有一个唯一的类别标记。KNN的主要思想就是计算每个训练数据到待分类元组的距离,取离待分类元组最近的k个训练数据,k个训练数据中哪一类别的训练数据占多数,待分类元组就属于哪个类别。
k-最临近算法
输入:训练数据T
最临近数目k
待分析的元组t
输出:t的类别c
N = Φ \Phi ΦFOR each d ∈ \in ∈T DO BEGIN
IF |N| < k THEN
N = N ∩ \cap ∩ {d}
ELSE
IF ∃ \exists ∃ u ∈ \in ∈N such that sim(u, t) < sim(d, t) THEN
BEGIN
N = N - {u};
N = N ∩ \cap ∩{d}
END
END
c = class related to such u ∈ \in ∈N which has the most number
优点:
- 简单、易于理解、容易实现
- 通过对k的选择可具备丢噪音数据的健壮性
缺点:
- 算法的时间复杂度高
- 占用大量存储空间
- 对k值的依赖性
- 当其样本分布不平衡时,如当其中一类样本占主导时,新的未知实例容易被归为主导样本
决策树 ID3
信息熵(information Entropy):对随机变量不确定度的度量,熵越大,随机变量的不确定性就越大
H ( p ) = − ∑ x p ( x ) l o g 2 ( p ( x ) ) H(p) = -\sum_xp(x)log_2(p(x)) H(p)=−x∑p(x)log2(p(x))
信息增益(information gain):是针对一个一个特征来的,就是看一个特征,系统有它和没有它时信息量各是多少,两者的差值即这个特征给系统带来的信息量,即信息增益
I G ( T ) = E n t r o p y ( S ) − E n t r o p y ( S ∣ T ) IG(T) = Entropy(S)- Entropy(S|T) IG(T)=Entropy(S)−Entropy(S∣T)
信息增益比:
G a i n R a t i o ( S , A ) = G a i n ( S , A ) S p l i t I n f o r m a t i o n ( S , A ) S p l i t I n f o r m a t i o n ( S , A ) = − ∑ j = 1 v p j l o g 2 ( p j ) GainRatio(S,A) = \frac{Gain(S,A)}{SplitInformation(S,A)}\\ SplitInformation(S,A) = -\sum^v_{j=1}p_jlog_2(p_j) GainRatio(S,A)=SplitInformation(S,A)Gain(S,A)SplitInformation(S,A)=−j=1∑vpjlog2(pj)
预剪枝(Pre-Pruning):在构造决策树的同时进行剪枝;设定一个阈值,如决策树根的长度等,构造决策树时不能超过这个阈值。
后剪枝(Post-Pruning):在决策树构造之后进行剪枝;从树的叶子节点开始剪枝,逐步向根的方法剪。剪枝的过程是对拥有同一父节点的一组节点进行检查,如果将其合并后增加的熵小于某个阈值,则将其合并为一个节点。其中包含了所有可能的结果。
贝叶斯分类
H : 所 属 类 别 X : 某 种 特 征 P ( H ∣ X ) = P ( X ∣ H ) P ( H ) P ( X ) H:所属类别\\ X:某种特征\\ P(H|X) = \frac{P(X|H)P(H)}{P(X)} H:所属类别X:某种特征P(H∣X)=P(X)P(X∣H)P(H)
P(H) 先验概率(prior probability):根据以往的经验和分析得到的概率
P(H|X) 后验概率(posterior probability):已知结果发生的情况下,求导致结果的某种原因的可能性的大小
EM算法(Expectation-Maximization Algorithm)
概念:在概率模型中寻找参数最大似然预计或者最大后验预计的算法。用于寻找,依赖于不可观察的隐性变量的概率模型中,参数的最大似然预计。
基本思想:分为两步Expection-step和Maximization-step,E-step通过已知数据和现有模型估计参数,然后用这个估计的参数计算似然函数的期望值;M-step是寻找似然函数最大化时对应的参数。由于算法会保证在每次迭代后似然函数都会增加,所以函数最终会趋于收敛
EM算法流程:
-
初始化分布参数
-
反复直到收敛
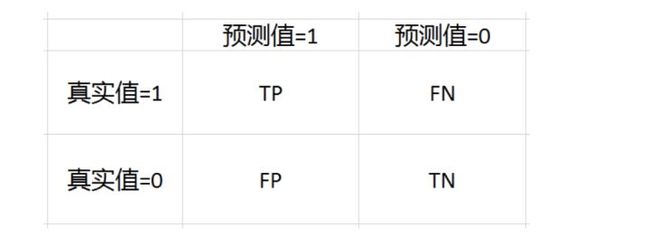
混淆矩阵
记忆:第二个字母P/N表示预测值,预测为1就为P,预测为0就为N;第一个字母T/F,表示预测的对不对,预测对了就为T,预测错了就为F
Accuracy(准确率)
A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy = \frac{TP+TN}{TP+TN+FP+FN} Accuracy=TP+TN+FP+FNTP+TN
P:precision(精确率)
P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP
r:recall(召回率/灵敏度)
r = T P T P + F N r=\frac{TP}{TP+FN} r=TP+FNTP
F β = ( 1 + β 2 ) P ∗ r β 2 ∗ P + r F_\beta=(1+\beta^2)\frac{P*r}{\beta^2*P+r} Fβ=(1+β2)β2∗P+rP∗r
评估分类方法:
-
保持法
在保持法中,把给定的数据随机地划分为两个独立的集合:训练集和测试集。通常,三分之一的数据为训练集,三分之二的数据为测试集。使用训练集得到分类器,其准确率用测试集评估
-
交叉验证
把数据随机的分为n等份,每份的大小基本相同,测试和训练都进行n次。
如:把数据分为10等份,其中一份保留用作测试,其余九份合在一起来建立模型,然后用那一份数据来测试建立的模型,得到错误率。对每一份都重复此步骤,得到十个错误率,最后模型用所有数据生成,错误率取十个错误率的平均。
第五章 聚类
聚类的概念:把数据分成不同的组,使组与组之间的差距尽可能的大,组内间的差距尽可能小
聚类分析在数据挖掘中的应用
- 聚类分析可以作为其他算法的预处理步骤
- 可以作为一个独立的工具来获得数据的分布情况
- 聚类分析可以完成孤立点挖掘
距离与相似性的度量
-
距离函数
-
明可夫斯基距离(Minkowski)
d ( x , y ) = ∑ i = 1 n ∣ x i − y i ∣ r r d(x,y) = \sqrt[r]{\sum_{i=1}^n|x_i-y_i|^r} d(x,y)=ri=1∑n∣xi−yi∣r
当r=1时,演变为绝对值距离/曼哈顿距离
d ( x , y ) = ∑ i = 1 n ∣ x i − y i ∣ d(x,y) = \sum_{i=1}^n|x_i-y_i| d(x,y)=i=1∑n∣xi−yi∣
当r=2时,演变为欧式距离
d ( x , y ) = ∑ i = 1 n ∣ x i − y i ∣ 2 2 d(x,y) = \sqrt[2]{\sum_{i=1}^n|x_i-y_i|^2} d(x,y)=2i=1∑n∣xi−yi∣2 -
余弦距离
d ( x , y ) = ∑ i = 1 n x i ∗ y i ∑ i = 1 n x i 2 ∗ ∑ i = 1 n y i 2 2 d(x,y)=\frac{\sum_{i=1}^nx_i*y_i}{\sqrt[2]{\sum_{i=1}^nx_i^2*\sum_{i=1}^ny_i^2}} d(x,y)=2∑i=1nxi2∗∑i=1nyi2∑i=1nxi∗yi -
相似度Jaccard系数
J ( A , B ) = ∣ A ∩ B ∣ ∣ A ∣ + ∣ B ∣ − ∣ A ∩ B ∣ d j = 1 − J ( A , B ) J(A,B)=\frac{|A\cap B|}{|A|+|B|-|A\cap B|}\\ \\ d_j= 1-J(A,B) J(A,B)=∣A∣+∣B∣−∣A∩B∣∣A∩B∣dj=1−J(A,B)
-
-
类间距离(如何计算聚类簇之间的距离?)
-
最短距离法
定义两个类中距离最近的两个元素间的距离为类间距离
-
最长距离
定义两个类中距离最远的两个元素元素间的距离为类间距离
-
中心法(均值距离)
定义两个类中心间的距离为类间距离
-
类平均法(平均距离)
任意两个元素距离的平均值作为类间距离
D C ( C a , C b ) = ∑ x ∈ C a ∑ y ∈ C b d ( x , y ) m n m : C a 类 的 元 素 个 数 n : C b 类 的 元 素 个 数 D_C(C_a,C_b)=\frac{\sum_{x\in C_a}\sum_{y\in C_b}d(x,y)}{mn}\\ \\ m:C_a类的元素个数\\ n:C_b类的元素个数 DC(Ca,Cb)=mn∑x∈Ca∑y∈Cbd(x,y)m:Ca类的元素个数n:Cb类的元素个数
-
K-Means算法
思想:k-平均算法以k为参数,将n个对象划分为k个簇,以使簇内具有较高的相似度。相似度的计算根据一个簇中对象的平均值来进行。
过程:算法首先随机的选择k个对象,以此作为初始的k个簇的中心或平均值,对剩余的每个对象根据其到各个簇中心的距离,将它划分给最近的簇,然后重新计算每个簇平均值,这个过程不断重复,直到准则函数E收敛。
E = ∑ i = 1 k ∑ x ∈ C i ∣ x − x ˉ i ∣ 2 E=\sum_{i=1}^k\sum_{x\in C_i}|x-\bar x_i|^2 E=i=1∑kx∈Ci∑∣x−xˉi∣2
K-Means(k-平均算法)
输入:簇的数目k,n个对象的数据库
输出:k个簇,使平方误差准则最小
assign inivate value for means
REPEAT
FOR j = 1 to n DO assign each x j x_j xj to the cluster which has the closest means;
FOR i = 1 to k DO x ˉ i \bar x_i xˉi = ∑ x ∈ C i x ∣ C i ∣ \sum_{x\in C_i}\frac{x}{|C_i|} ∑x∈Ci∣Ci∣x;
Compute E
UNTIL E收敛
PAM(Partitioning Around Medoid)围绕中心点的划分
思想:最初随机选择k个对象作为中心点,该算法反复的用非代表对象来替换代表对象,视图找出更好的中心点,以改变聚类的质量。
过程:
- 建立:随机寻找k个中心点作为类中心
- 对所有可能的对象对进行分析,找到交换后可以使平方-误差减小最大的对象,代替原中心点
层次聚类方法
AGNES算法
AGNES(自底向上凝聚算法)
输入:包含n个对象的数据库,终止的条件簇数目k
输出:k个簇,达到终止条件规定的簇数目
将每个对象当成一个初始簇
REPEAT
根据两个簇中最近的数据点找到最近的两个簇
合并这两个簇,生成新的簇的集合
UNTIL 达到终止条件定义的簇的数目
算法例子
| 序号 | 属性1 | 属性2 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 2 |
| 3 | 2 | 1 |
| 4 | 2 | 2 |
| 5 | 3 | 4 |
| 6 | 3 | 5 |
| 7 | 4 | 4 |
| 8 | 4 | 5 |
执行过程
| 步骤 | 最近的簇距离 | 最近的两个簇 | 合并后的新簇 |
|---|---|---|---|
| 1 | 1 | {1},{2} | {1,2},{3},{4},{5},{6},{7},{8} |
| 2 | 1 | {3},{4} | {1,2},{3,4},{5},{6},{7},{8} |
| 3 | 1 | {5},{6} | {1,2},{3,4},{5,6},{7},{8} |
| 4 | 1 | {7},{8} | {1,2},{3,4},{5,6},{7,8} |
| 5 | 1 | {1,2}{3,4} | {1,2,3,4},{5,6},{7,8} |
| 6 | 1 | {5,6}{7,8} | {1,2,3,4},{5,6,7,8} |
DIANA算法
DIANA(自顶向下分裂算法)
输入:包含n个对象的数据库,簇的终止数目k
输出:k个簇,达到终止条件规定簇的数目
将所有对象合成一个初始簇
FOR (i = 1; i ≠ \neq = k; i++ ) DO BEGIN
找到所有簇中直径最大的簇 找出所选簇中与其他点平均差异度最大的点加入splinter group中,其余点放入old party中
REPEAT
在old party中找出到splinter group点中最近距离不大于到old party点中最近距离的点,加入到splinter group中
UNTIL 没有新的old party的点分配给splinter group
splinter group 和 old party两个簇为被选定的簇分裂成的,与其他簇一起组成新的簇集合
END;
算法执行例子
| 序号 | 属性1 | 属性2 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 2 |
| 3 | 2 | 1 |
| 4 | 2 | 2 |
| 5 | 3 | 4 |
| 6 | 3 | 5 |
| 7 | 4 | 4 |
| 8 | 4 | 5 |
执行过程
| 步骤 | 具有最大直径的簇 | splinter group | old party |
|---|---|---|---|
| 1 | {1,2,3,4,5,6,7,8} | {1} | {2,3,4,5,6,7,8} |
| 2 | {1,2,3,4,5,6,7,8} | {1,2} | {3,4,5,6,7,8} |
| 3 | {1,2,3,4,5,6,7,8} | {1,2,3} | {4,5,6,7,8} |
| 4 | {1,2,3,4,5,6,7,8} | {1,2,3,4} | {5,6,7,8} |
| 5 | {1,2,3,4,5,6,7,8} | {1,2,3,4} | {5,6,7,8}终止 |
DBSCAN
DBSCAN(Density-Based Spatial Clustering of Applications with Noise) 基于密度的噪声应用空间聚类
输入:包含n个对象的数据库,半径 ε \varepsilon ε,最小数目MinPts
输出:所有生成的簇,达到密度要求
REPEAT
从数据库中抽取一个未被处理过的点
IF 抽取的点使中心点,THEN 找出所有的密度可达的对象,形成一个簇
ELSE 抽取的点是边缘点(非核心对象),则跳过本次循环,继续查找下一点
UNTIL 所有的点都被处理
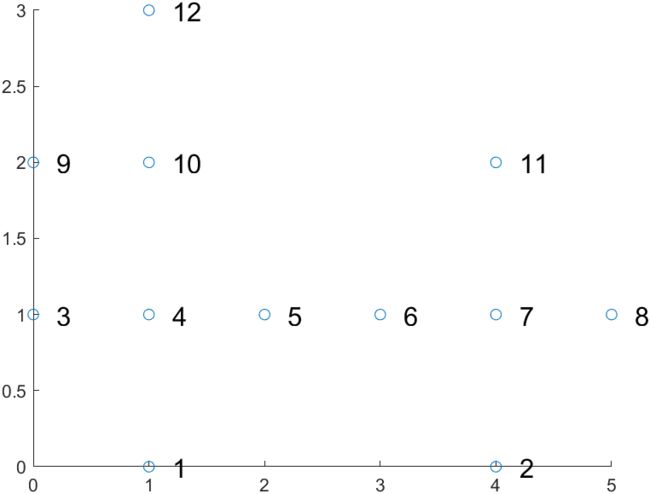
算法执行例子( ε \varepsilon ε = 1, MinPts = 4)
| 序号 | 属性1 | 属性2 |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 4 | 0 |
| 3 | 0 | 1 |
| 4 | 1 | 1 |
| 5 | 2 | 1 |
| 6 | 3 | 1 |
| 7 | 4 | 1 |
| 8 | 5 | 1 |
| 9 | 0 | 2 |
| 10 | 1 | 2 |
| 11 | 4 | 2 |
| 12 | 1 | 3 |
执行过程
| 步骤 | 选择的点 | 在 ε \varepsilon ε中的个数 | 通过计算可达点而找到的新簇 |
|---|---|---|---|
| 1 | 1 | 2 | 无 |
| 2 | 2 | 2 | 无 |
| 3 | 3 | 3 | 无 |
| 4 | 4 | 5 | C 1 C_1 C1{1,3,4,5,9,10,12} |
| 5 | 5 | 3 | 已在一个簇 C 1 C_1 C1中 |
| 6 | 6 | 3 | 无 |
| 7 | 7 | 5 | C 2 C_2 C2{2,6,7,8,11} |
| 8 | 8 | 2 | 已在一个簇 C 2 C_2 C2中 |
| 9 | 9 | 3 | 已在一个簇 C 1 C_1 C1中 |
| 10 | 10 | 4 | 已在一个簇 C 1 C_1 C1中 |
| 11 | 11 | 2 | 已在一个簇 C 2 C_2 C2中 |
| 12 | 12 | 2 | 已在一个簇 C 1 C_1 C1中 |
第六章 时间序列和序列模式挖掘
-
时间序列
时间序列就是将某一指标在不同时间上的不同数值,按照时间的先后顺序排列而成的序列
-
时间序列数据挖掘
时间序列挖掘就是要从大量的时间序列数据中提取出人们事先不知道的、潜在有用的、与时间属性相关的信息和知识,并用于短期、中期或长期预测,指导人们社会、生活、军事、经济等行为。
第七章 PageRank
基于随机冲浪的PageRank算法
输入:页面链接网络G
输出:页面等级值向量R
设置点击概率d,等级值向量初始值 R 0 R_0 R0,迭代终止条件 ε \varepsilon ε
根据根据页面链接网络G生成转移概念矩阵M
i = 1;
REPEAT
R i + 1 R_{i+1} Ri+1 = M R i R_i Ri;
ε i \varepsilon_i εi = || R i + 1 − R i R_{i+1} - R_i Ri+1−Ri||
UNTIL ε i < ε \varepsilon_i < \varepsilon εi<ε
Return R i + 1 R_{i+1} Ri+1
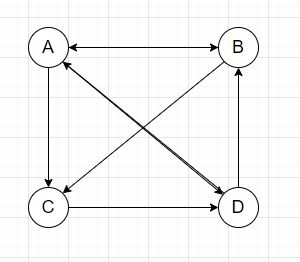
执行例子
[已在matlab运行]https://gitee.com/wu-yuhaohao/picture/tree/master/matlab)
A = [
[0,1/2,0,1/2],
[1/3,0,0,1/2],
[1/3,1/2,0,0],
[1/3,0, 1, 0]
]
A =
0 0.5000 0 0.5000
0.3333 0 0 0.5000
0.3333 0.5000 0 0
0.3333 0 1.0000 0
Q = [
[1/4,1/4,1/4,1/4],
[1/4,1/4,1/4,1/4],
[1/4,1/4,1/4,1/4],
[1/4,1/4,1/4,1/4]
]
Q =
0.2500 0.2500 0.2500 0.2500
0.2500 0.2500 0.2500 0.2500
0.2500 0.2500 0.2500 0.2500
0.2500 0.2500 0.2500 0.2500
d = 0.85
d =
0.8500
M = (1-d)Q + dA
M =
0.0375 0.4625 0.0375 0.4625
0.3208 0.0375 0.0375 0.4625
0.3208 0.4625 0.0375 0.0375
0.3208 0.0375 0.8875 0.0375
R = ones(4,1)
R =
1
1
1
1
R1 = M*R
R1 =
1.0000
0.8583
0.8583
1.2833
varepsilon = sum(sum(abs(R1-R)))
varepsilon =
0.5667
R2 = M*R1
R2 =
1.0602
0.9787
0.7981
1.1629
varepsilon = sum(sum(abs(R2-R1)))
varepsilon =
0.3612
R3 = M*R2
R3 =
1.0602
0.9446
0.8664
1.1288
varepsilon = sum(sum(abs(R3-R2)))
varepsilon =
0.1365
R4 = M*R3
R4 =
1.0312
0.9301
0.8519
1.1868
varepsilon = sum(sum(abs(R4-R3)))
varepsilon =
0.1160
R5 = M*R4
R5 =
1.0497
0.9466
0.8375
1.1663
varepsilon = sum(sum(abs(R5-R4)))
varepsilon =
0.0698