机器学习-降维方法：PCA、KPCA、LDA、LLE、LE、t-SNE、AutoEncoder、MDS、ISOMAP、FastICA、SVD、LPP、ICA

$$\begin{array}{r}\text{无监督学习}\{\begin{array}{l}\text{化繁为简}\{\begin{array}{l}\text{聚类(Clustering)}\{\begin{array}{l}\text{k-Means算法}\\ \text{k-Means++算法}\\ \text{密度聚类算法}\{\begin{array}{l}\text{DBSCAN算法}\\ \text{密度最大值聚类算法}\end{array}\\ \text{谱聚类算法}\\ \text{GMM(高斯混合模型)聚类算法}\\ \text{Topic Model(主题模型)算法}\{\begin{array}{l}\text{LDA(隐含狄利克雷分布)}\\ \text{PLSA(概率隐语义)}\\ \text{LFM}\\ \text{LSI}\end{array}\end{array}\\ \text{降维(Dimension Reduction)}\{\begin{array}{l}\text{线性降维}\{\begin{array}{l}\text{主成分分析(Principal Component Analysis)}\\ \text{因子分析(Feature selection)}\end{array}\\ \text{非线性降维}\{\begin{array}{l}\text{核化线性(KPCA)降维}\\ \text{t-SNE}\\ \text{多维标度法（MDS）}\\ \text{Restricted Boltzmann Machine}\\ \text{Deep Belief Network}\\ \text{等距离映射(Isomap)}\\ \text{局部线性嵌入（LLE）}\end{array}\end{array}\end{array}\\ \text{无中生有}：\text{Generation}\end{array}\end{array}$$

一、主成分分析(PCA/Principal Component Analysis)

本质：PCA是一种分析、简化数据集的技术(当特征数量达到上百的时候，考虑数据的简化)。
目的：是数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。在降低维度时，尽可能减少损失。
作用：可以削减回归分析或者聚类分析中特征的数量。
用到的类：sklearn.decomposition

• 主成分分析（Principal Component Analysis，PCA）是一种 Linear Dimension Reduction(线性降维)
• 主成分分析（Principal Component Analysis，PCA）：是一种无监督统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。
• 在很多情形，变量之间是有一定的相关关系的，当两个变量之间有一定相关关系时，可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量，将重复的变量（关系紧密的变量）删去多余，建立尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映课题的信息方面尽可能保持原有的信息。
• 设法将原来变量重新组合成一组新的互相无关的几个综合变量，同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析，也是数学上用来降维的一种方法。

高维度数据容易出现的问题：特征之间通常是线性相关的或近似线性相关。

1、PCA理论基础：正交变换

正交向量：指点乘积(数量积)为零的两个或多个向量，若向量 $\alpha$ 与 $\beta$ 正交，则$\alpha$·$\beta$=0，记为 $\alpha$⊥$\beta$。

正交矩阵(orthogonal matrix)：是一个方块矩阵(方阵)，其元素为实数，而且行(列)向量两两正交且是单位向量，使得该矩阵的转置矩阵为其逆矩阵： $Q^T$ = Q⁻¹ ⇔ $Q^T$Q = Q$Q^T$ = E。
正交矩阵的行列式值必定为 + 1或 − 1。
作为一个线性映射（变换矩阵），正交矩阵保持距离不变，所以它是一个保距映射，具体例子为旋转与镜射。
行列式值为+1的正交矩阵，称为特殊正交矩阵，它是一个旋转矩阵。
行列式值为-1的正交矩阵，称为瑕旋转矩阵。瑕旋转是旋转加上镜射。镜射也是一种瑕旋转。

正交变换：是线性变换的一种，它从实内积空间V映射到V自身，且保证变换前后内积不变。因为向量的模长与向量间的夹角都是用内积定义的，所以正交变换前后一对向量各自的模长和它们的夹角都不变。

正交变换： Y’ = P * X = $\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]$ * $\left[\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right]$ = $\left[\begin{array}{ccccc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}& 0& \frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ -\frac{3}{\sqrt{2}}& -\frac{1}{\sqrt{2}}& 0& \frac{3}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]$

旋转矩阵(Rotation matrix)：是在乘以一个向量的时候有改变向量的方向但不改变大小的效果并保持了手性的矩阵。

通过旋转矩阵（属于正交矩阵，满足正交矩阵的一切性质）将原矩阵旋转到各个点的x分量(x₁, x₂, x₃, x₄ …)之间，或者y分量(y₁, y₂, y₃, y₄ …)之间，或者z分量(z₁, z₂, z₃, z₄ …)之间尽可能不相等。

二维旋转矩阵：$P$ = $\left[\begin{array}{cc}sin\theta & -sin\theta \\ cos\theta & cos\theta \end{array}\right]$ $\stackrel{\text{θ=45°}}{===}$ $\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]$

三维旋转矩阵：$P_x$ = $\left[\begin{array}{ccc}1& 0& 0\\ 0& cos{\theta }_x& -sin{\theta }_x\\ 0& sin{\theta }_x& cos{\theta }_x\end{array}\right]$；$P_y$ = $\left[\begin{array}{ccc}cos{\theta }_y& 0& sin{\theta }_y\\ 0& 1& 0\\ -sin{\theta }_y& 0& cos{\theta }_y\end{array}\right]$；$P_z$ = $\left[\begin{array}{ccc}cos{\theta }_z& -sin{\theta }_z& 0\\ sin{\theta }_z& cos{\theta }_z& 0\\ 0& 0& 1\end{array}\right]$

Y’矩阵的第2行数据(y数据)各不相同，可以用来做降维处理。选取旋转矩阵P的第二行作为变换矩阵，左乘矩阵X得到一个线性变换后的行矩阵(行向量)。由原来的特征x、特征y(2个)减少为特征y(1个)，而且该保留下来的特征y包含了原数据的大部分信息。

Y’ = P * X = $\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]$ * $\left[\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right]$ = $\left[\begin{array}{ccccc}-\frac{3}{\sqrt{2}}& -\frac{1}{\sqrt{2}}& 0& \frac{3}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]$

PCA有两种通俗易懂的解释：(1)最大方差理论；(2)最小化降维造成的损失。这两个思路都能推导出同样的结果。

最大方差理论：最好的 $k$ 维特征是将 $n$ 维样本点转换为 $k$ 维后，每一个维度上的样本方差都很大，数据更加发散。将这些更加发散的数据提供给算法进行训练时，更有利于得出更好的模型。

1. 样本 ${\text{X}}_{m\times n}$ （其中 $m$ 为样品数量，$n$ 为特征数量）在 ${\text{u}}_{n\times 1}$ 向量方向上的投影为 ${\text{X}}_{m\times n}\cdot \text{u}$，其方差 $var=({\text{X}}_{m\times n}\cdot \text{u}-\text{E}{)}^2=({\text{X}}_{m\times n}\cdot \text{u}-\text{E}{)}^T\cdot ({\text{X}}_{m\times n}\cdot \text{u}-\text{E})$
2. 令数据中心化，则 $\text{E}=\text{0}$
3. 方差 $var=({\text{X}}_{m\times n}\cdot \text{u}{)}^T\cdot ({\text{X}}_{m\times n}\cdot \text{u})={\text{u}}^T({\text{X}}^T\text{X}{)}_{n\times n}\text{u}$，此方差 $var$ 是关于 $\text{u}$ 的一个函数，问题转为：就 $var(u)$ 的极大值。
4. 令 $\text{u}$ 是单位向量，则 $|\text{u}|=1⟹{\text{u}}^T\cdot \text{u}=1$；
5. 问题转为求在约束条件 ${\text{u}}^T\cdot \text{u}=1$ 下，求 $var={\text{u}}^T({\text{X}}^T\text{X}{)}_{n\times n}\text{u}$ 的极大值；
6. 构造朗格朗日函数：$J(\text{u})={\text{u}}^T({\text{X}}^T\text{X}{)}_{n\times n}\text{u}+\lambda (1-{\text{u}}^T\cdot \text{u})$；
7. 求朗格朗日函数$J(\text{u})$对$\text{u}$的偏导，并令其为0，此时所求的 $\text{u}$ 即是约束条件 ${\text{u}}^T\cdot \text{u}=1$ 下函数 $var={\text{u}}^T({\text{X}}^T\text{X}{)}_{n\times n}\text{u}$ 的极大值处的 $\text{u}$；
8. $\begin{array}{r}\frac{\partial J(\text{u})}{\partial \text{u}}=\frac{\partial [{\text{u}}^T({\text{X}}^T\text{X}{)}_{n\times n}\text{u}+\lambda (1-{\text{u}}^T\cdot \text{u})]}{\partial \text{u}}=2({\text{X}}^T\text{X}{)}_{n\times n}\text{u}-2\lambda \text{u}=0\end{array}$；
9. $\text{∴}$ $\begin{array}{r}[({\text{X}}^T\text{X}{)}_{n\times n}]\text{u}=\lambda \text{u}\end{array}$；
10. $\text{∴}$ $\begin{array}{r}\{[({\text{X}}^T\text{X}{)}_{n\times n}]-\lambda \text{E}\}\text{u}=0\end{array}$
11. $\begin{array}{r}\{[({\text{X}}^T\text{X}{)}_{n\times n}]-\lambda \text{E}\}\text{u}=0\end{array}$ 是一个 $n$ 个未知数$n$ 个方程的齐次线性方程组，(参考：《线性代数》同济大学第六版 $p_{120}$)它有非零解的充分必要条件是系数行列式
    $$\begin{array}{r}\left|[({\text{X}}^T\text{X}{)}_{n\times n}]-\lambda \text{E}\right|=0\end{array}$$
12. $\text{∴}$ 求解未知数为 $\text{u}$ 的方程 $\begin{array}{r}[({\text{X}}^T\text{X}{)}_{n\times n}]\text{u}=\lambda \text{u}\end{array}$ 的解，就是求 方阵 $({\text{X}}^T\text{X}{)}_{n\times n}$ 的特征值 $\lambda$ 以及 各个特征值分别对应的 特征向量 $\text{u}$，其中 特征值 $\lambda$ 及其对应的特征向量 $\text{u}$ 的数量为 $n$；
13. 由于 方阵 $({\text{X}}^T\text{X}{)}_{n\times n}$ 是一个对称矩阵，所以求得的不同的特征值 $\lambda$ 对应的 特征向量 $\text{u}$ 之间两两正交(方向垂直)；
14. $\text{∴}$ PCA方法找方差 $var$ 最大时的方向向量 $\text{u}$，就是找第一主成分；PCA方法找方差 $var$ 第二大时的方向向量 $\text{u}$，就是找第二主成分；方阵 $({\text{X}}^T\text{X}{)}_{n\times n}$ 特征向量 的数量为 $n$ 个，求出的主成分的数量为 $n$ 个。
15. PCA主成分分析降维，就是从 $n$ 个相互垂直的方向向量 ${\text{u}}_{n\times 1}$ 中选取 $(n-k)$ 个方向向量${\text{u}}_{n\times 1}$ ，然后将 ${\text{X}}_{m\times n}$ 通过${\text{X}}_{m\times n}\times {\text{u}}_{n\times 1}^i$投影到各个 ${\text{u}}_{n\times 1}^i$方向上，得到各个方向向量 ${\text{u}}_{n\times 1}^i$ (特征$i$)上的 数据 ${\text{X}}_{m\times 1}^i$，或者通过将 $n$ 个相互垂直的方向向量 ${\text{u}}_{n\times 1}$ 通过加权平均得到 $(n-k)$ 个方向向量 ${\text{u}}_{n\times 1}^i$ (特征$i$)上的 数据 ${\text{X}}_{m\times 1}^i$。

2、PCA语法

2.1 PCA(n_components=None)

• 实例化，将数据分解为较低维数空间。
• n_components可以为0~1的小数或整数。
• n_components取小数时，表示PCA主成分分析之后信息保留量的百分比。经验表明一般填写0.9~0.95之间的小数。
• n_components取整数时，表示PCA主成分分析之后所保留的特征的数量。一般不用此参数。

2.2 PCA.fit_transform(X)

X:numpy array格式的数据[n_samples,n_features]，返回值：转换后指定维度的array

3、PCA降维案例

3.1 PCA降维案例01

from sklearn.decomposition import PCA

def pca():
    """主成分分析进行特征降维"""
    pca070 = PCA(n_components=0.70)
    data070 = pca070.fit_transform([[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]])
    print('data070 = \n', data070)
    pca080 = PCA(n_components=0.80)
    data080 = pca080.fit_transform([[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]])
    print('data080 = \n', data080)
    pca099 = PCA(n_components=0.99)
    data099 = pca099.fit_transform([[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]])
    print('data099 = \n', data099)
    return None

if __name__ == "__main__":
    pca()

打印结果：

data070 = 
 [[ 1.28620952e-15]
 [ 5.74456265e+00]
 [-5.74456265e+00]]
data080 = 
 [[ 1.28620952e-15  3.82970843e+00]
 [ 5.74456265e+00 -1.91485422e+00]
 [-5.74456265e+00 -1.91485422e+00]]
data099 = 
 [[ 1.28620952e-15  3.82970843e+00]
 [ 5.74456265e+00 -1.91485422e+00]
 [-5.74456265e+00 -1.91485422e+00]]

结果表明：

• 当n_components=0.70时，由原来的4个特征，最后保留了1个特征；
• 当n_components=0.80 时，由原来的4个特征，最后保留了2个特征；保留了原始数据的近80%的信息量。
• 当n_components=0.99 时，由原来的4个特征，最后保留了2个特征；保留了原始数据的近99%的信息量。

4、降维方法“特征选择”与“主成分分析”的选择

如果特征数量特别多(比如上百个)，则选择主成分分析的方法来降维；

二、LDA(Linear Discriminant Analysis, 线性判别分析)算法

• LDA是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。
• PCA是不考虑样本类别输出的无监督降维技术。
• LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”。什么意思呢？ 我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。
  
• 当然在实际应用中，我们的数据是多个类别的，我们的原始数据一般也是超过二维的，投影后的也一般不是直线，而是一个低维的超平面。

1、LDA算法的优缺点：

1.1 优点：

1. 在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识。
2. LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。

1.2 缺点：

1. LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。
2. LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
3. LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。
4. LDA可能过度拟合数据。

2、LDA vs PCA

LDA用于降维，和PCA有很多相同，也有很多不同的地方，因此值得好好的比较一下两者的降维异同点。

1、相同点

1. 两者均可以对数据进行降维。
2. 两者在降维时均使用了矩阵特征分解的思想。
3. 两者都假设数据符合高斯分布。

2、不同点

1. LDA是有监督的降维方法，而PCA是无监督的降维方法
2. LDA降维最多降到类别数k-1的维数，而PCA没有这个限制。
3. LDA除了可以用于降维，还可以用于分类。
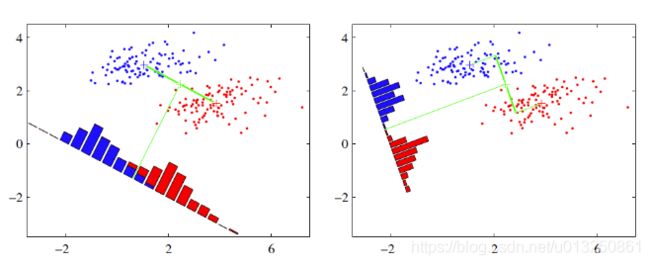
4. LDA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。
5. 这点可以从下图形象的看出，在某些数据分布下LDA比PCA降维较优。
   
   当然，某些某些数据分布下PCA比LDA降维较优，如下图所示：
   

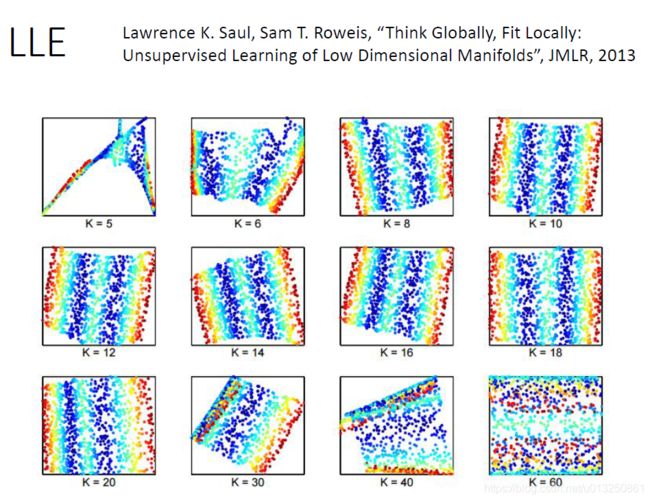
三、Locally Linear Embedding(LLE)

调超参数：

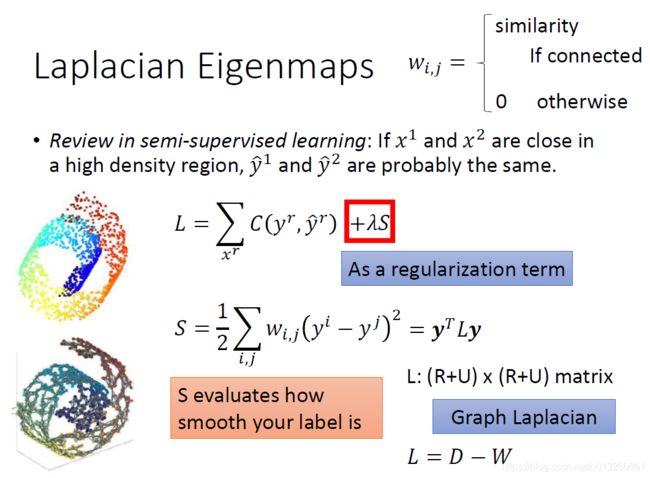
四、Laplacian Eigenmaps(LE)

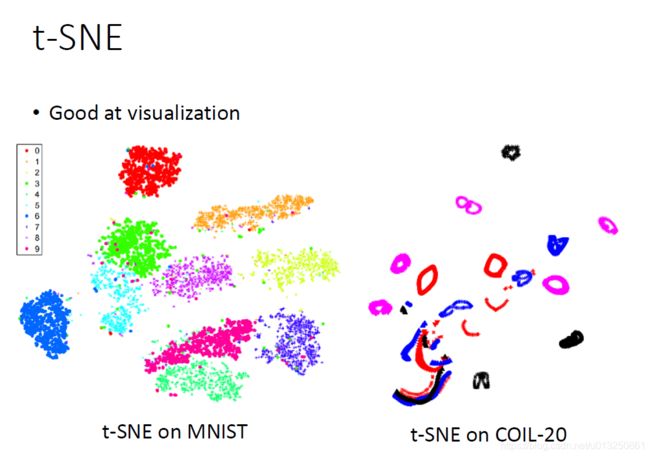
五、t-distributed Stochastic Neighbor Embedding (t-SNE)

• t-SNE计算量比较大，可以先用PCA降维降到一定程度，然后再用TSNE降维。
  
  

六、Autoencoder(AE)

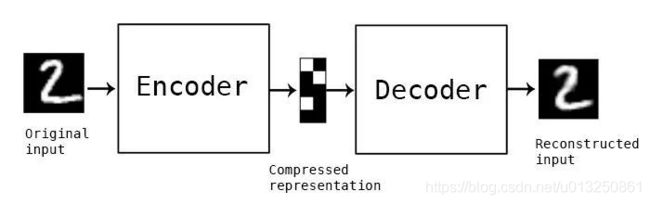
• 所谓自编码器（Autoencoder，AE），就是一种利用反向传播算法使得输出值等于输入值的神经网络，
• 它先将输入压缩成潜在空间表征，然后将这种压缩后的空间表征重构为输出。
  
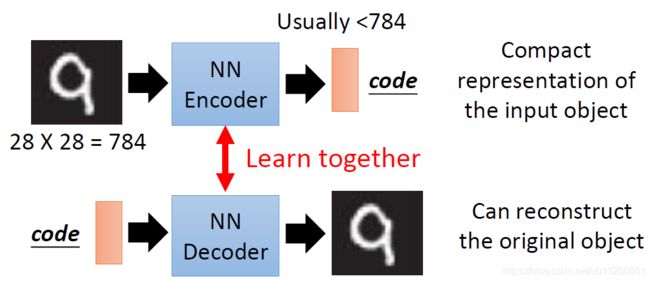
• 它的隐藏成层的向量具有降维的作用。所以，从本质上来讲，自编码器是一种数据压缩算法，其压缩和解压缩算法都是通过神经网络来实现的。
• 自编码器有如下三个特点：
  1. 数据相关性。就是指自编码器只能压缩与自己此前训练数据类似的数据，比如说我们使用mnist训练出来的自编码器用来压缩人脸图片，效果肯定会很差。
  2. 数据有损性。自编码器在解压时得到的输出与原始输入相比会有信息损失，所以自编码器是一种数据有损的压缩算法。
  3. 自动学习性。自动编码器是从数据样本中自动学习的，这意味着很容易对指定类的输入训练出一种特定的编码器，而不需要完成任何新工作。
• 构建一个自编码器需要两部分：编码器（Encoder）和解码器（Decoder）。
• 编码器将输入压缩为潜在空间表征，编码器会创建一个隐藏层（或多个隐藏层）包含了输入数据含义的低维向量。可以用函数 $f(x)$ 来表示，
• 解码器将潜在空间表征重构为输出，即通过隐藏层的低维向量重建输入数据。可以用函数 $g(x)$ 来表示
• 编码函数 $f(x)$ 和解码函数 $g(x)$ 都是神经网络模型。
  
  
  
  
  
  

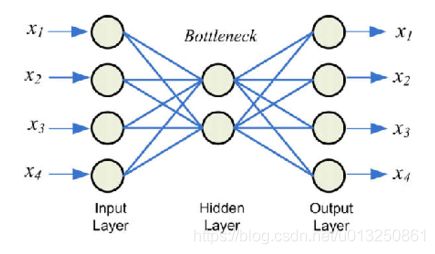
1、自编码器(AutoEncoder)损失函数

• AE是一个自动编码器是一个非监督的学习模式，只需要输入数据，不需要label或者输入输出对的数据。
• 虽然AE是一个非监督学习算法，如果它的解码器是线性重建数据，可以用MSE来表示它的损失函数：
  
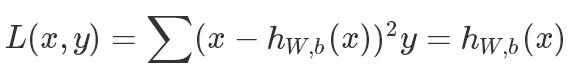
• 如果解码器用Sigmoid的激活函数，那主要用交叉上损失函数：
  

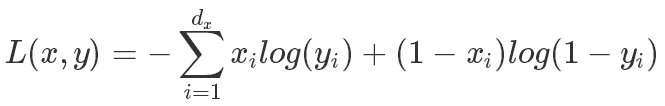
2、自编码器(AutoEncoder)模型

AE的思想是在1986年被提出来的，在接下来的几年，AE的思想席卷了个大研究论文。关于AE比较有代表性的模型有一下几种：

2.1 Denoising AutoEncoder

• DAE的主要做法是，输入数据加入了噪声，输出的数据是完整的数据。DAE会强制隐藏层只去学习主要的特征，输出的数据就会是更好的鲁棒性。
• DAE的一种方式是随机的删除数据集中的某些数据，然后用完整的数据去评判，DAE会尝试去预测恢复缺失的部分。
• 一个关于手写数字集的DAE的展示图如下：
  
  

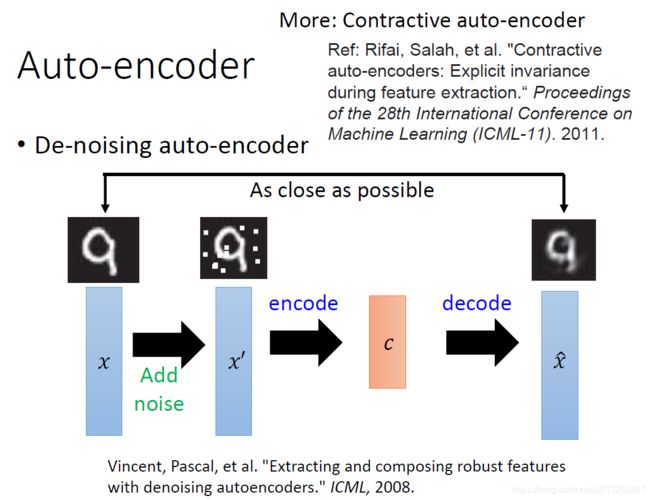
2.2 Sparse AutoEncoder

• AE一般的方式是通过隐藏层中的少数的隐藏单元去发现有用的信息，但是AE也可以通过大量的隐藏单元去发现有用信息。
• SAE的做法是把输入数据转化为高纬度的中间层，然后引入一个稀疏限制的规则。稀疏限制是在大部分时间，大部分的神经元的平均输出比较低。
• 如果使用Sigmoid的激活函数，我们会尽量把输出变为0，如果是tanh的激活函数，我们会尽量把输出变为-1。
  
  $a_j$ 是神经元的激活后的输出，$p_j$ 是所有神经元输出的平均值，我们的目标是去最小化 $p_j$。
• K-Sparse AutoEncoder是SAE提升版本，KSAE是本身的隐藏神经元非常多，但只选择k个神经元是激活的，其他都是dropout状态，通过选择不同的激活函数和调整不同的k的阈值去训练。下面是通过调整k值，生成不同的手写数字的输出值。
  

2.3 Contractive AutoEncoder

• CAE的主要目标是使得隐藏层向量对输入数据的微小的变动能够有更强的鲁棒性。CAE的做法是在普通AE的基础上加上一个惩罚项。公式如下：
  
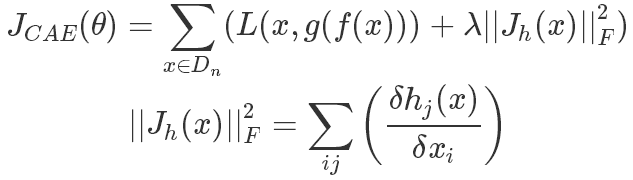
  CAE和DAE目标是相似的，DAE是通过加入噪声，重构来提升模型的鲁棒性，CAE是通过增加雅克比矩阵的惩罚项来提高模型鲁棒性。

2.4 Variational AutoEncoder

• VAE结构是一个经典的autocoder模型，网络的组成也是编码器、解码器、loss。
• VAE的机构和普通的AE结构有所不同。
• 普通的AE结构如下，解码器直接使用编码器的输出向量。
  
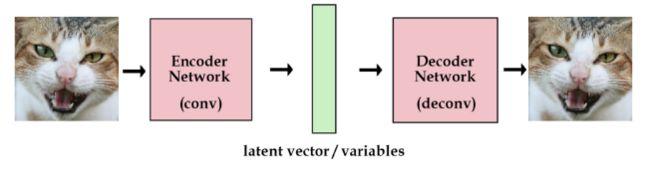
• 上面的模型已经可以训练任意图片了。但是，我们想建一个产生式模型，而不是一个只是储存图片的网络。
• 现在我们还不能产生任何未知的东西，因为我们不能随意产生合理的潜在变量。因为合理的潜在变量都是编码器从原始图片中产生的。
• 这里有个简单的解决办法。我们可以对编码器添加约束，就是强迫它产生服从单位高斯分布的潜在变量。正是这种约束，把VAE和标准自编码器给区分开来了。
• 不像标准自编码器那样产生实数值向量，VAE的编码器会产生两个向量:一个是均值向量，一个是标准差向量。
  
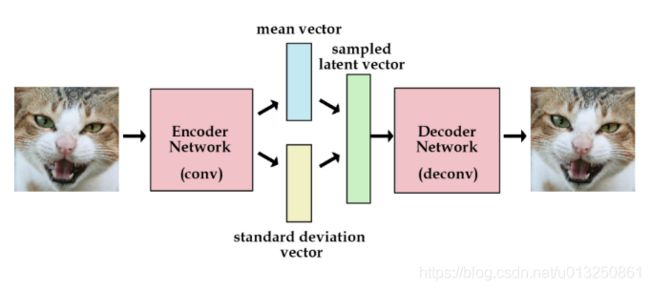
• VAE除了能让我们能够自己产生随机的潜在变量，这种约束也能提高网络的产生图片的能力。
• 另外，VAE的一个劣势就是没有使用对抗网络，所以会更趋向于产生模糊的图片

3、AutoEncoder用途

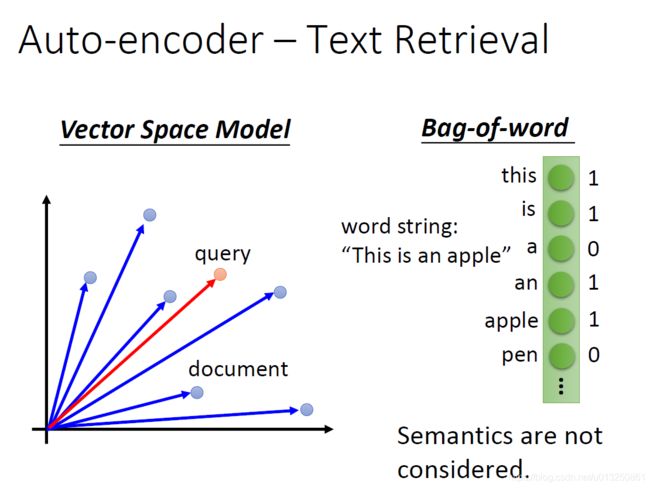
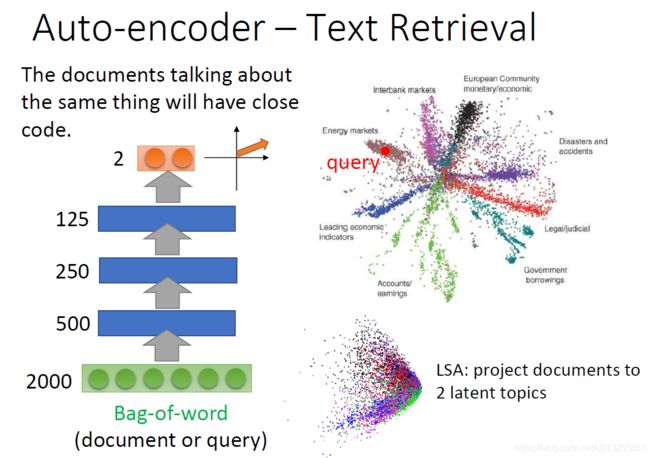
3.1 AutoEncoder用于Text Retrieval

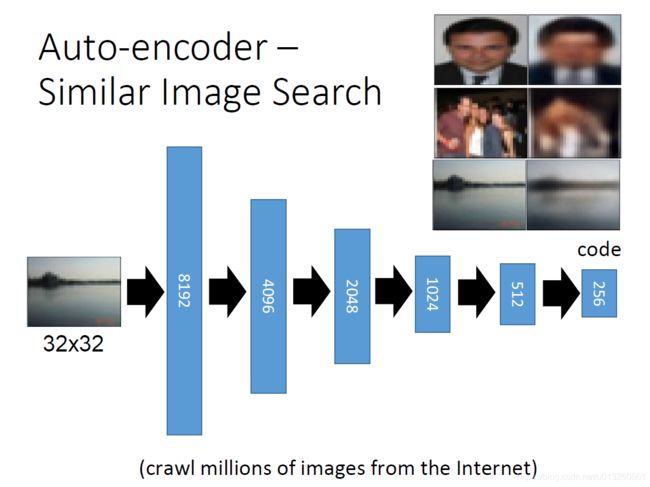
3.2 AutoEncoder用于Similar Image Search

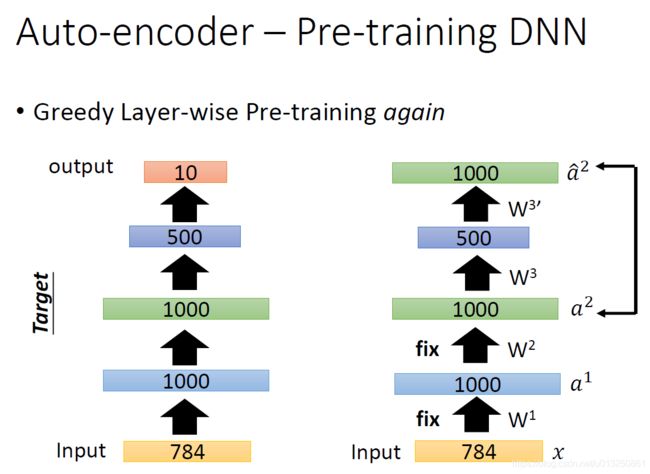
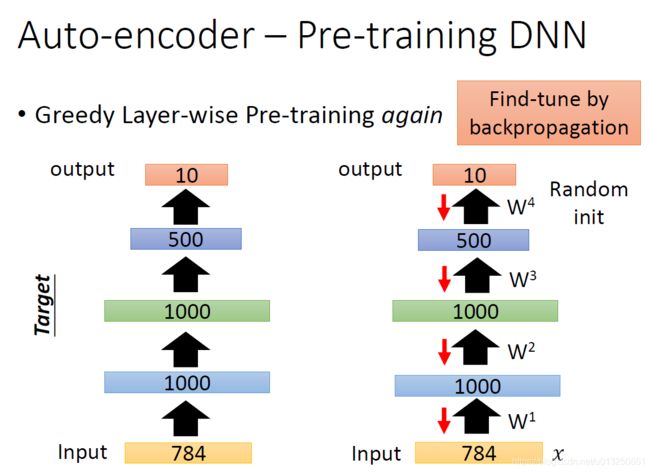
3.3 AutoEncoder用于Pre-training DNN(初始化)

• 现在的network 比较强大，基本不用Pre-training，但是当数据集中有大量unlabel 数据时AutoEncoder做Pre-training还是有用的
  
  
  
  

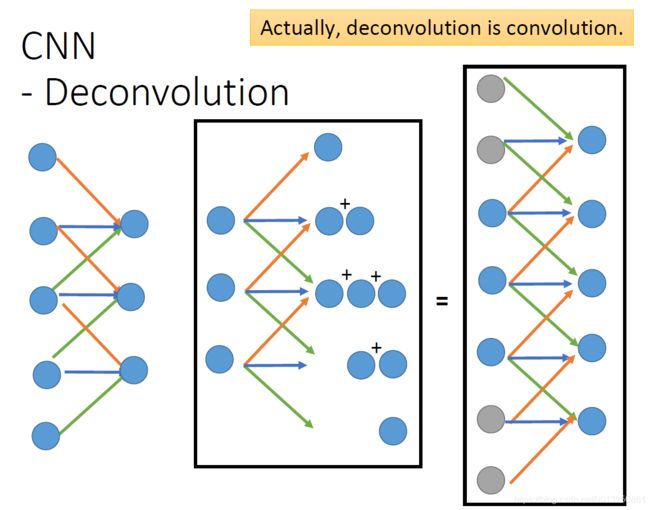
3.4 AutoEncoder用于CNN

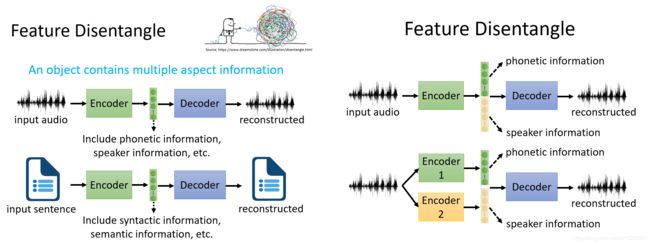
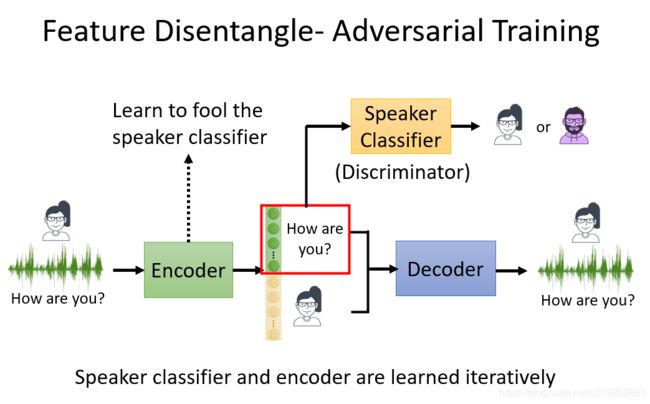
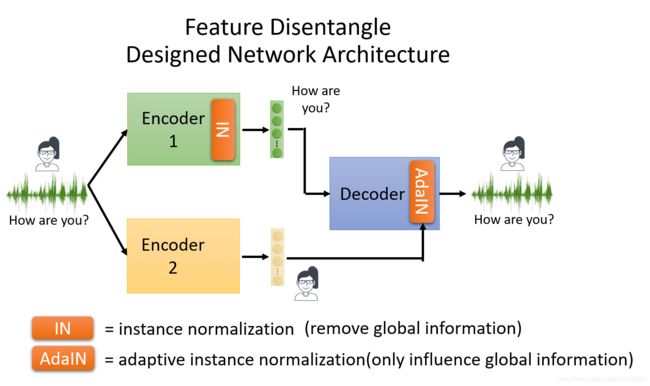
4、Feature Disentangle用于变声器(Voice Conversion)

---

---

---

参考资料：
降维方法总结（线性与非线性）
Singular Value Decomposition
PCA、LDA、MDS、LLE、TSNE等降维算法的Python实现
LDA 线性判别分析(降维)——还没看懂
SNE,tSNE和LargeVis
使用t-SNE可视化图像embedding
sklearn中tsne可视化
Python实现TSNE
TSNE 高维数据可视化
第五章：深度生成模型
第二十章 深度生成模型
三大深度学习生成模型：VAE、GAN及其变种
深度学习笔记 | 第17讲：深度生成模型之自编码器(AutoEncoder)
AutoEncoder介绍
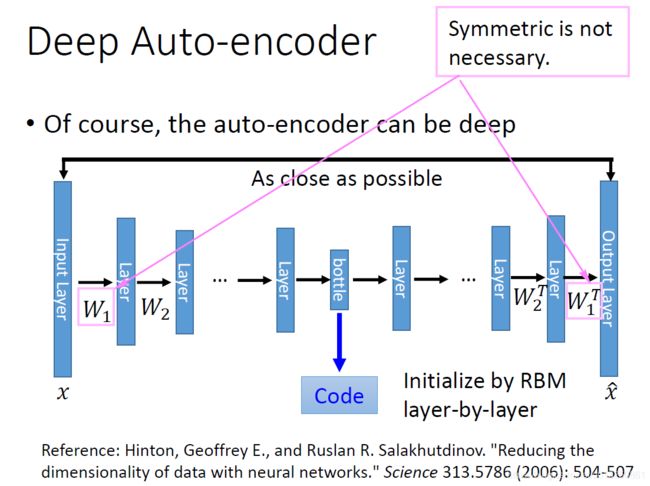
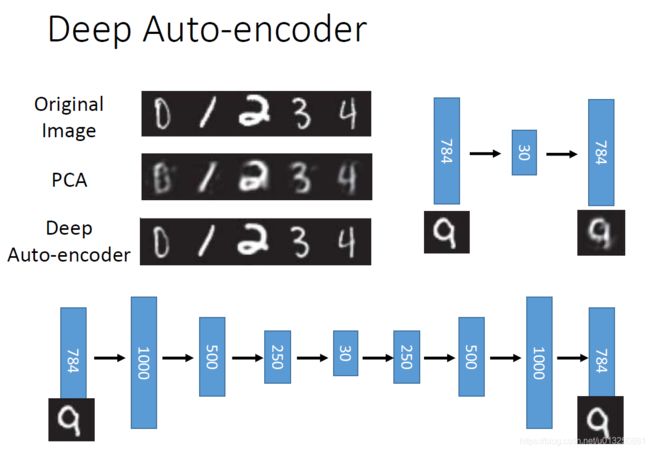
李宏毅深度学习笔记-无监督学习-深度自动编码器