【机器学习基础】(四):通俗理解支持向量机SVM及代码实践
上一篇文章我们介绍了使用逻辑回归来处理分类问题,本文我们讲一个更强大的分类模型。本文依旧侧重代码实践,你会发现我们解决问题的手段越来越丰富,问题处理起来越来越简单。
支持向量机(Support Vector Machine, SVM)是最受欢迎的机器学习模型之一。它特别适合处理中小型复杂数据集的分类任务。
一、什么是支持向量机
SMV在众多实例中寻找一个最优的决策边界,这个边界上的实例叫做支持向量,它们“支持”(支撑)分离开超平面,所以它叫支持向量机。
那么我们如何保证我们得到的决策边界是最优的呢?
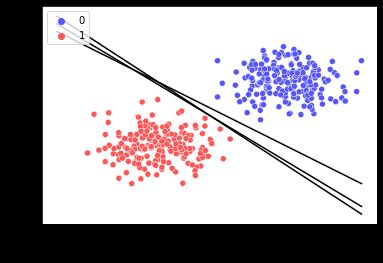
如上图,三条黑色直线都可以完美分割数据集。由此可知,我们仅用单一直线可以得到无数个解。那么,其中怎样的直线是最优的呢?
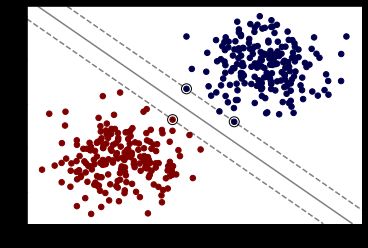
如上图,我们计算直线到分割实例的距离,使得我们的直线与数据集的距离尽可能的远,那么我们就可以得到唯一的解。最大化上图虚线之间的距离就是我们的目标。而上图中重点圈出的实例就叫做支持向量。
这就是支持向量机。
二、从代码中映射理论
2.1 导入数据集
添加引用:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
导入数据集(大家不用在意这个域名):
df = pd.read_csv('https://blog.caiyongji.com/assets/mouse_viral_study.csv')
df.head()
| Med_1_mL | Med_2_mL | Virus Present | |
|---|---|---|---|
| 0 | 6.50823 | 8.58253 | 0 |
| 1 | 4.12612 | 3.07346 | 1 |
| 2 | 6.42787 | 6.36976 | 0 |
| 3 | 3.67295 | 4.90522 | 1 |
| 4 | 1.58032 | 2.44056 | 1 |
该数据集模拟了一项医学研究,对感染病毒的小白鼠使用不同剂量的两种药物,观察两周后小白鼠是否感染病毒。
特征:1. 药物Med_1_mL 药物Med_2_mL
标签:是否感染病毒(1感染/0不感染)
2.2 观察数据
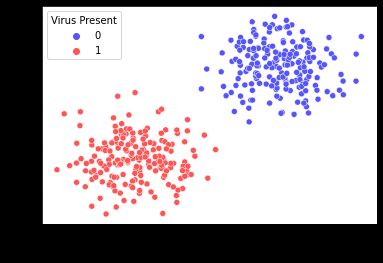
sns.scatterplot(x='Med_1_mL',y='Med_2_mL',hue='Virus Present',data=df)
我们用seaborn绘制两种药物在不同剂量特征对应感染结果的散点图。
sns.pairplot(df,hue='Virus Present')
我们通过pairplot方法绘制特征两两之间的对应关系。
我们可以做出大概的判断,当加大药物剂量可使小白鼠避免被感染。
2.3 使用SVM训练数据集
#SVC: Supprt Vector Classifier支持向量分类器
from sklearn.svm import SVC
#准备数据
y = df['Virus Present']
X = df.drop('Virus Present',axis=1)
#定义模型
model = SVC(kernel='linear', C=1000)
#训练模型
model.fit(X, y)
# 绘制图像
# 定义绘制SVM边界方法
def plot_svm_boundary(model,X,y):
X = X.values
y = y.values
# Scatter Plot
plt.scatter(X[:, 0], X[:, 1], c=y, s=30,cmap='coolwarm')
# plot the decision function
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)
# plot decision boundary and margins
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
# plot support vectors
ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100,
linewidth=1, facecolors='none', edgecolors='k')
plt.show()
plot_svm_boundary(model,X,y)
我们导入sklearn下的SVC(Supprt Vector Classifier)分类器,它是SVM的一种实现。
2.4 SVC参数C
SVC方法参数C代表L2正则化参数,正则化的强度与C的值成反比,即C值越大正则化强度越弱,其必须严格为正。
model = SVC(kernel='linear', C=0.05)
model.fit(X, y)
plot_svm_boundary(model,X,y)
我们减少C的值,可以看到模型拟合数据的程度减弱。
2.5 核技巧
SVC方法的kernel参数可取值{'linear', 'poly', 'rbf', 'sigmoid', 'precomputed'}。像前文中所使用的那样,我们可以使kernel='linear'进行线性分类。那么如果我们想进行非线性分类呢?
2.5.1 多项式内核
多项式内核kernel='poly'的原理简单来说就是,用单一特征生成多特征来拟合曲线。比如我们拓展X到y的对应关系如下:
| X | X^2 | X^3 | y | |
|---|---|---|---|---|
| 0 | 6.50823 | 6.50823**2 | 6.50823**3 | 0 |
| 1 | 4.12612 | 4.12612**2 | 4.12612**3 | 1 |
| 2 | 6.42787 | 6.42787**2 | 6.42787**3 | 0 |
| 3 | 3.67295 | 3.67295**2 | 3.67295**3 | 1 |
| 4 | 1.58032 | 1.58032**2 | 1.58032**3 | 1 |
这样我们就可以用曲线来拟合数据集。
model = SVC(kernel='poly', C=0.05,degree=5)
model.fit(X, y)
plot_svm_boundary(model,X,y)
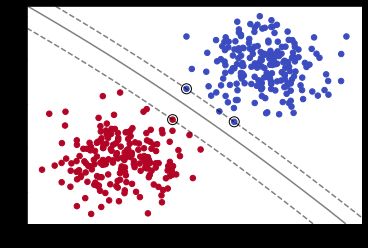
我们使用多项式内核,并通过degree=5设置多项式的最高次数为5。我们可以看出分割出现了一定的弧度。
2.5.2 高斯RBF内核
SVC方法默认内核为高斯RBF,即Radial Basis Function(径向基函数)。这时我们需要引入gamma参数来控制钟形函数的形状。增加gamma值会使钟形曲线变得更窄,因此每个实例影响的范围变小,决策边界更不规则。减小gamma值会使钟形曲线变得更宽,因此每个实例的影响范围变大,决策边界更平坦。
model = SVC(kernel='rbf', C=1,gamma=0.01)
model.fit(X, y)
plot_svm_boundary(model,X,y)
2.6 调参技巧:网格搜索
from sklearn.model_selection import GridSearchCV
svm = SVC()
param_grid = {'C':[0.01,0.1,1],'kernel':['rbf','poly','linear','sigmoid'],'gamma':[0.01,0.1,1]}
grid = GridSearchCV(svm,param_grid)
grid.fit(X,y)
print("grid.best_params_ = ",grid.best_params_,", grid.best_score_ =" ,grid.best_score_)
我们可以通过GridSearchCV方法来遍历超参数的各种可能性来寻求最优超参数。这是通过算力碾压的方式暴力调参的手段。当然,在分析问题阶段,我们必须限定了各参数的可选范围才能应用此方法。
因为数据集太简单,我们在遍历第一种可能性时就已经得到100%的准确率了,输出如下:
grid.best_params_ = {'C': 0.01, 'gamma': 0.01, 'kernel': 'rbf'} , grid.best_score_ = 1.0
总结
当我们处理线性可分的数据集时,可以使用SVC(kernel='linear')方法来训练数据,当然我们也可以使用更快的方法LinearSVC来训练数据,特别是当训练集特别大或特征非常多的时候。
当我们处理非线性SVM分类时,可以使用高斯RBF内核,多项式内核,sigmoid内核来进行非线性模型的的拟合。当然我们也可以通过GridSearchCV寻找最优参数。
往期文章:
机器学习(三):理解逻辑回归及二分类、多分类代码实践
机器学习(二):理解线性回归与梯度下降并做简单预测
机器学习(一):5分钟理解机器学习并上手实践
前置机器学习(五):30分钟掌握常用Matplotlib用法
前置机器学习(四):一文掌握Pandas用法
前置机器学习(三):30分钟掌握常用NumPy用法
前置机器学习(二):30分钟掌握常用Jupyter Notebook用法
前置机器学习(一):数学符号及希腊字母
![]()
往期精彩回顾
适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载机器学习的数学基础专辑
本站qq群704220115,加入微信群请扫码: