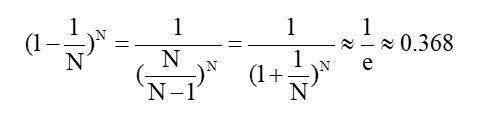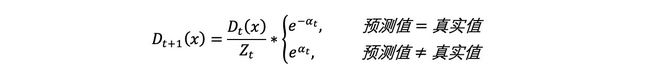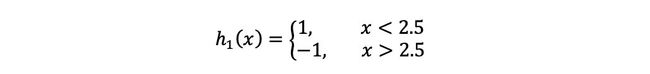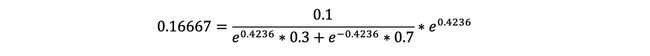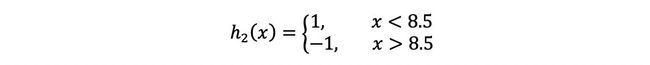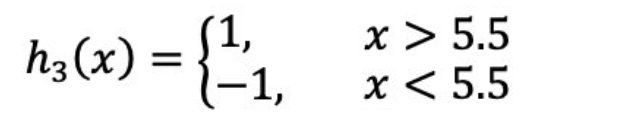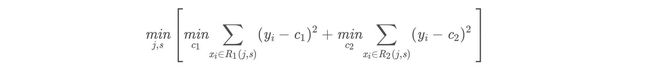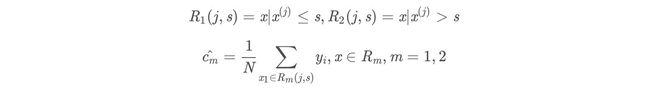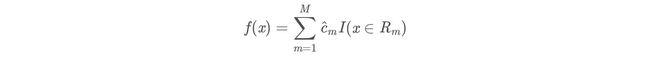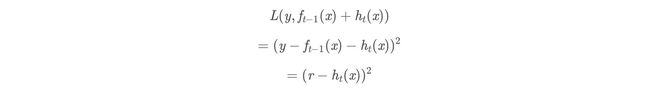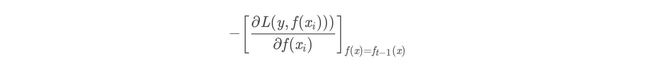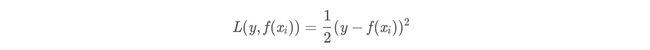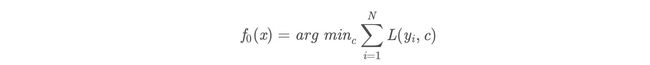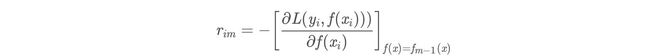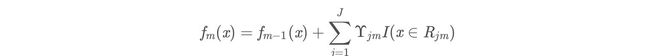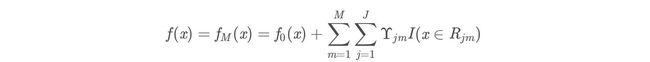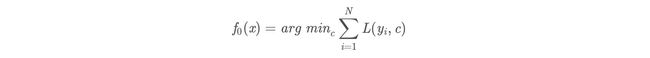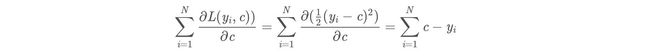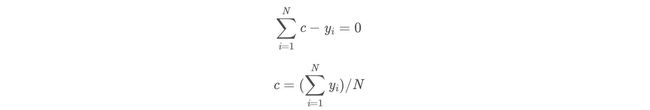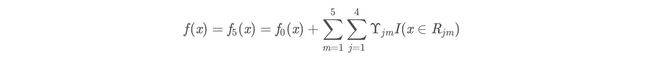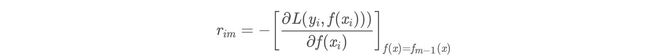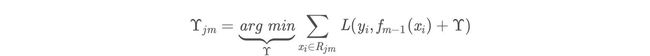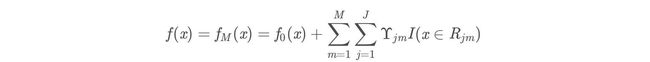Python_机器学习_算法_第5章_集成学习基础

Python_机器学习_算法_第5章_集成学习基础

集成学习基础

学习目标

• 了解什么是集成学习
• 知道机器学习中的两个核心任务
• 知道Bagging集成原理
• 知道随机森林构造过程
• 知道RandomForestClassifier的使用
• 知道boosting集成原理和实现过程
• 知道bagging和boosting集成的区别
• 知道AdaBoost集成原理
• 知道GBDT的算法原理

5.1 集成学习算法简介

学习目标

• 了解什么是集成学习
• 知道机器学习中的两个核心任务
• 了解集成学习中的boosting和bagging

---

1 什么是集成学习

集成学习通过建立几个模型来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立地学习和作出预测。这些预测最后结合成组合预测，因此优于任何一个单分类的做出预测。

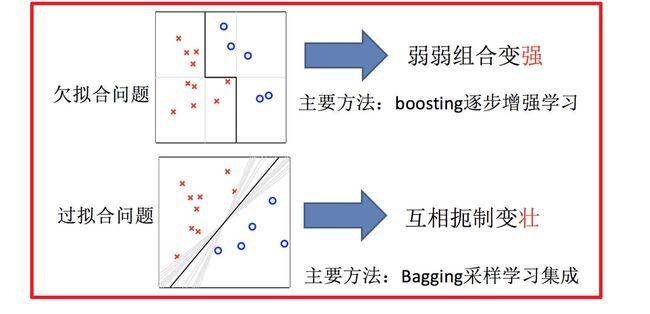
2 复习：机器学习的两个核心任务

• 任务一：如何优化训练数据 —> 主要用于解决欠拟合问题
• 任务二：如何提升泛化性能 —> 主要用于解决过拟合问题

3 集成学习中boosting和Bagging

只要单分类器的表现不太差，集成学习的结果总是要好于单分类器的

---

4 小结

• 什么是集成学习【了解】
  • 通过建立几个模型来解决单一预测问题
• 机器学习两个核心任务【知道】
  • 1.解决欠拟合问题
    • 弱弱组合变强
    • boosting
  • 2.解决过拟合问题
    • 互相遏制变壮
    • Bagging

5.2 Bagging和随机森林

学习目标

• 知道Bagging集成原理
• 知道随机森林构造过程
• 知道什么是包外估计
• 知道RandomForestClassifier的使用
• 了解baggind集成的优点

---

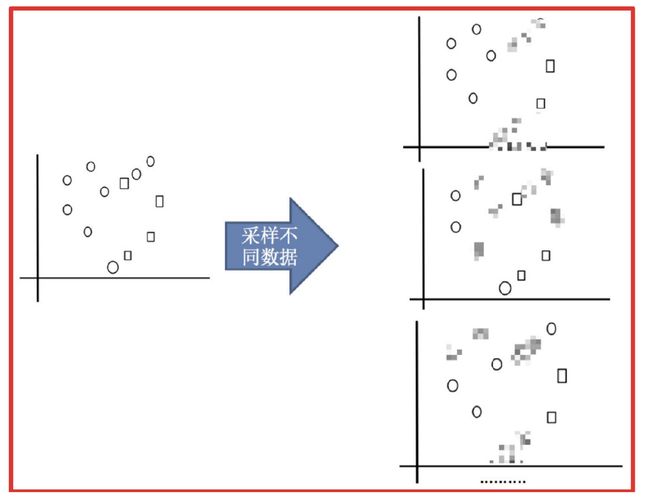
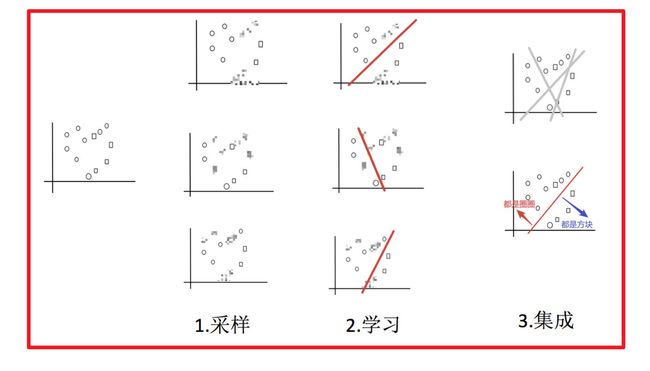
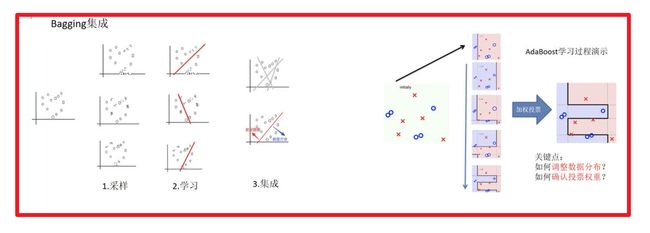
1 Bagging集成原理

目标：把下面的圈和方块进行分类

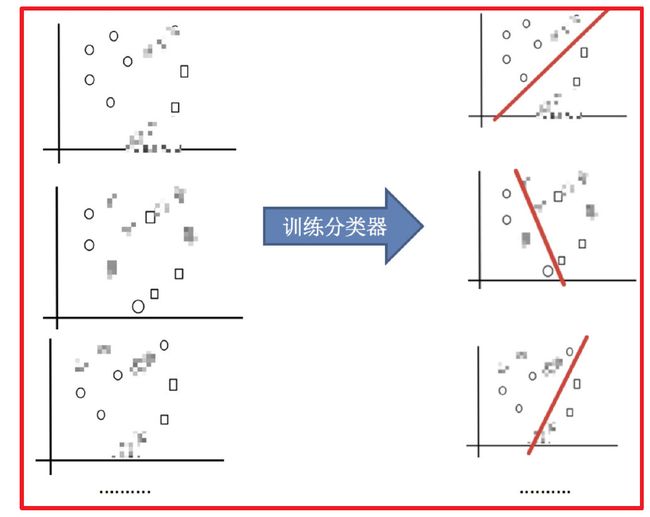
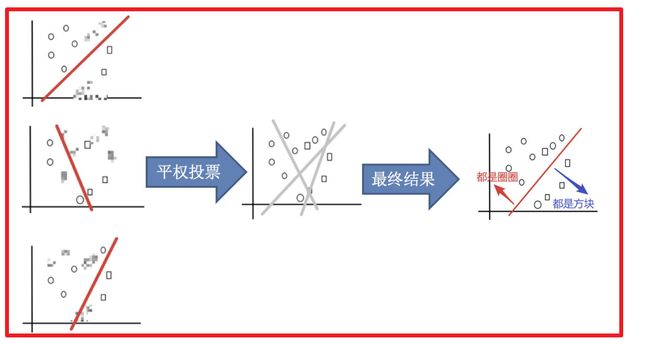
实现过程：

1. 采样不同数据集

2)训练分类器

3)平权投票，获取最终结果

4)主要实现过程小结

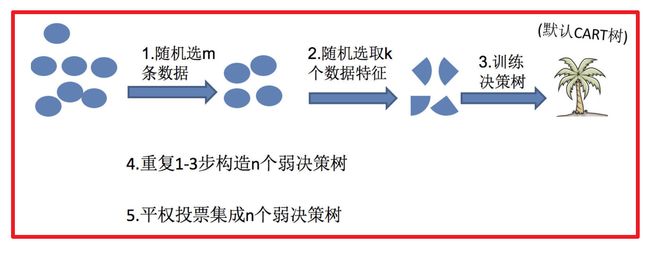
2 随机森林构造过程

在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

随机森林 = Bagging + 决策树

例如, 如果你训练了5个树, 其中有4个树的结果是True, 1个树的结果是False, 那么最终投票结果就是True

随机森林够造过程中的关键步骤(M表示特征数目)：

1)一次随机选出一个样本，有放回的抽样，重复N次(有可能出现重复的样本)

2) 随机去选出m个特征, m <

• 思考
  • 1.为什么要随机抽样训练集？
    • 如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的
  • 2.为什么要有放回地抽样？
    • 如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是“有偏的”，都是绝对“片面的”(当然这样说可能不对)，也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树(弱分类器)的投票表决。

3 包外估计

在随机森林构造过程中，如果进行有放回的抽样，我们会发现，总是有一部分样本我们选不到。

• 这部分数据，占整体数据的比重有多大呢？
• 这部分数据有什么用呢？

3.1 包外估计的定义

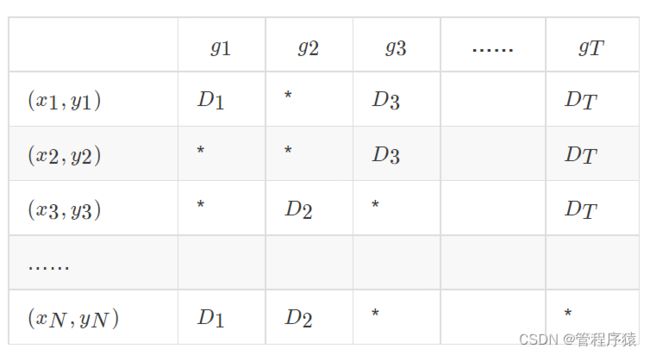
随机森林的 Bagging 过程，对于每一颗训练出的决策树 gt ，与数据集 D 有如下关系：

	g*1	g*2	g*3	……	g**T*
((x1,y1)	D*1	*	D*3		D**T*
(x2,y2)	*	*	D*3		D**T*
(x3,y3)	*	D*2	*		D**T*
……
(xN,yN)	D1	D*2	*		*

对于星号的部分，即是没有选择到的数据，称之为 Out-of-bag(OOB)数据，当数据足够多，对于任意一组数据 (xn, yn) 是包外数据的概率为：

由于基分类器是构建在训练样本的自助抽样集上的，只有约 63.2％ 原样本集出现在中，而剩余的 36.8％ 的数据作为包外数据，可以用于基分类器的验证集。

经验证，包外估计（ Out-of-Bag Estimate）是对集成分类器泛化误差的无偏估计.

在随机森林算法中数据集属性的重要性、分类器集强度和分类器间相关性计算都依赖于袋外数据。

3.2 包外估计的用途

• 当基学习器是决策树时，可使用包外样本来辅助剪枝 ，或用于估计决策树中各结点的后验概率以辅助对零训练样本结点的处理；
• 当基学习器是神经网络时，可使用包外样本来辅助早期停止以减小过拟合 。

4 随机森林api介绍

• sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)

  • n_estimators：integer，optional(default = 10)森林里的树木数量120,200,300,500,800,1200

    • 在利用最大投票数或平均值来预测之前，你想要建立子树的数量。

  • Criterion：string，可选(default =“gini”)

    • 分割特征的测量方法

  • max_depth：integer或None，可选(默认=无)

    • 树的最大深度 5,8,15,25,30

  • max_features="auto”,每个决策树的最大特征数量

    • If “auto”, then max_features=sqrt(n_features).
    • If “sqrt”, then max_features=sqrt(n_features)(same as “auto”).
    • If “log2”, then max_features=log2(n_features).
    • If None, then max_features=n_features.

  • bootstrap：boolean，optional(default = True)

    • 是否在构建树时使用放回抽样

  • min_samples_split 内部节点再划分所需最小样本数

    • 这个值限制了子树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分，默认是2。
    • 如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。

  • min_samples_leaf 叶子节点的最小样本数

    • 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝， 默认是1。

    • 叶是决策树的末端节点。 较小的叶子使模型更容易捕捉训练数据中的噪声。

    • 一般来说，我更偏向于将最小叶子节点数目设置为大于50。

  • min_impurity_split: 节点划分最小不纯度

    • 这个值限制了决策树的增长，如果某节点的不纯度(基于基尼系数，均方差)小于这个阈值，则该节点不再生成子节点。即为叶子节点 。

    • 一般不推荐改动默认值1e-7。

• 上面决策树参数中最重要的包括

  • 最大特征数max_features，
  • 最大深度max_depth，
  • 内部节点再划分所需最小样本数min_samples_split
  • 叶子节点最少样本数min_samples_leaf。

5 随机森林预测案例

• 实例化随机森林

# 随机森林去进行预测
rf = RandomForestClassifier()

• 定义超参数的选择列表

param = {"n_estimators": [120,200,300,500,800,1200], "max_depth": [5, 8, 15, 25, 30]}

• 使用GridSearchCV进行网格搜索

# 超参数调优
gc = GridSearchCV(rf, param_grid=param, cv=2)

gc.fit(x_train, y_train)

print("随机森林预测的准确率为：", gc.score(x_test, y_test))

注意

• 随机森林的建立过程
• 树的深度、树的个数等需要进行超参数调优

6 bagging集成优点

Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法

经过上面方式组成的集成学习方法:

1. 均可在原有算法上提高约2%左右的泛化正确率
2. 简单, 方便, 通用

---

7 小结

• bagging集成过程【知道】
  • 1.采样 — 从所有样本里面，采样一部分
  • 2.学习 — 训练弱学习器
  • 3.集成 — 使用平权投票
• 随机森林介绍【知道】
  • 随机森林定义
    • 随机森林 = Bagging + 决策树
  • 流程：
    • 1.随机选取m条数据
    • 2.随机选取k个特征
    • 3.训练决策树
    • 4.重复1-3
    • 5.对上面的若决策树进行平权投票
  • 注意：
    • 1.随机选取样本，且是有放回的抽取
    • 2.选取特征的时候吗，选择m<
    • M是所有的特征数
  • 包外估计
    • 如果进行有放回的对数据集抽样，会发现，总是有一部分样本选不到；
  • api
    • sklearn.ensemble.RandomForestClassifier()
• Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法【了解】
• bagging的优点【了解】
  • 1.均可在原有算法上提高约2%左右的泛化正确率
  • 2.简单, 方便, 通用

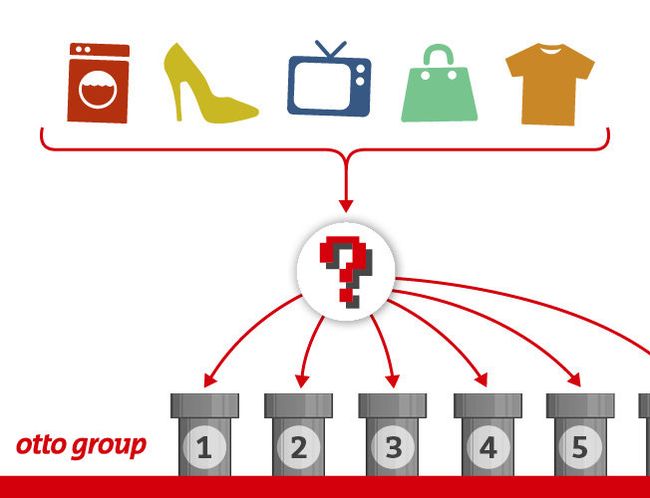
5.3 otto案例介绍 – Otto Group Product Classification Challenge

1.背景介绍

奥托集团是世界上最大的电子商务公司之一，在20多个国家设有子公司。该公司每天都在世界各地销售数百万种产品,所以对其产品根据性能合理的分类非常重要。

不过,在实际工作中,工作人员发现,许多相同的产品得到了不同的分类。本案例要求,你对奥拓集团的产品进行正确的分类。尽可能的提供分类的准确性。

链接：https://www.kaggle.com/c/otto-group-product-classification-challenge/overview

2.数据集介绍

• 本案例中，数据集包含大约200,000种产品的93个特征。
• 其目的是建立一个能够区分otto公司主要产品类别的预测模型。
• 所有产品共被分成九个类别（例如时装，电子产品等）。

• id - 产品id
• feat_1, feat_2, …, feat_93 - 产品的各个特征
• target - 产品被划分的类别

3.评分标准

本案例中，最后结果使用多分类对数损失进行评估。

具体公式：

上公式中，

• N：样本数
• M：类别数
• Pij：代表第i个样本属于类别j的概率（i表示样本，j表示类别。）
• 如果第i个样本真的属于类别j，则yij等于1，否则为0。

---

• 根据上公式，假如你将所有的测试样本都正确分类，所有pij都是1，那每个log(pij)都是0，最终的logloss也是0。
• 假如第1个样本本来是属于1类别的，但是你给它的类别概率pij=0.1，那logloss就会累加上log(0.1)这一项。我们知道这一项是负数，而且pij越小，负得越多，如果pij=0，将是无穷。这会导致这种情况：你分错了一个，logloss就是无穷。这当然不合理，为了避免这一情况，我们对非常小的值做如下处理：

• 也就是说最小不会小于10^-15。

4.实现过程

4.1 流程分析

• 获取数据
• 数据基本处理
  • 数据量比较大，尝试是否可以进行数据分割
  • 转换目标值表示方式
• 模型训练
  • 模型基本训练

4.2 代码实现

• 具体见【[RF]OTTO Group Product Classification Challenge.ipynb】

5.4 Boosting

学习目标

• 知道boosting集成原理和实现过程
• 知道bagging和boosting集成的区别
• 知道AdaBoost集成原理

---

1 什么是boosting

随着学习的积累从弱到强

简而言之：每新加入一个弱学习器，整体能力就会得到提升

代表算法：Adaboost，GBDT，XGBoost，LightGBM

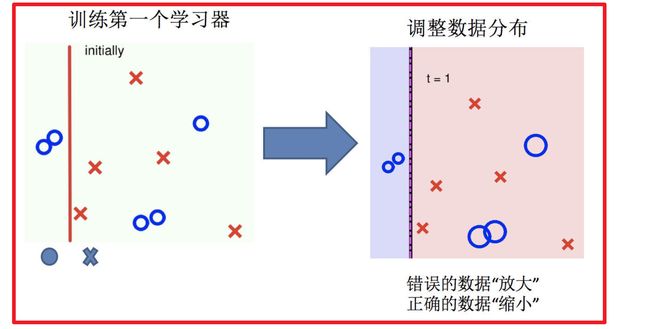
2 实现过程：

1.训练第一个学习器

2.调整数据分布

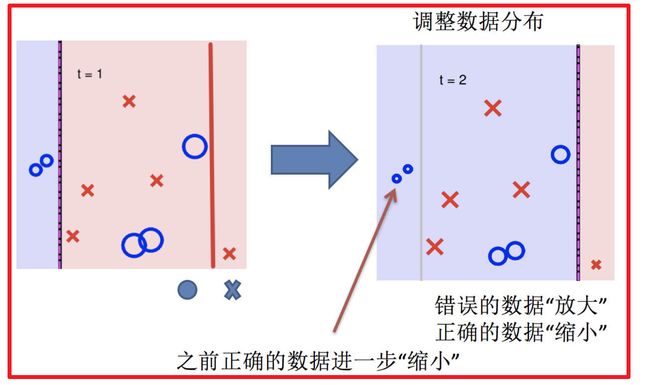
3.训练第二个学习器

4.再次调整数据分布

5.依次训练学习器，调整数据分布

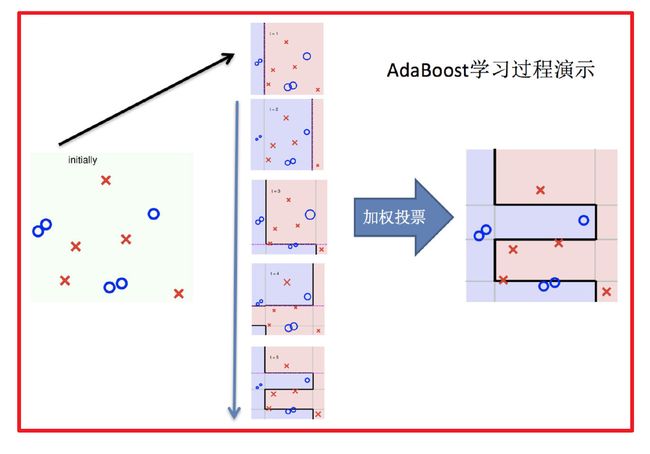
6.整体过程实现

3 bagging与boosting的区别

• 区别一:数据方面
  • Bagging：对数据进行采样训练；
  • Boosting：根据前一轮学习结果调整数据的重要性。
• 区别二:投票方面
  • Bagging：所有学习器平权投票；
  • Boosting：对学习器进行加权投票。
• 区别三:学习顺序
  • Bagging的学习是并行的，每个学习器没有依赖关系；
  • Boosting学习是串行，学习有先后顺序。
• 区别四:主要作用
  • Bagging主要用于提高泛化性能（解决过拟合，也可以说降低方差）
  • Boosting主要用于提高训练精度 （解决欠拟合，也可以说降低偏差）

4 AdaBoost介绍

4.1 构造过程细节

• 步骤一：初始化训练数据权重相等，训练第一个学习器。

  • 该假设每个训练样本在基分类器的学习中作用相同，这一假设可以保证第一步能够在原始数据上学习基本分类器H1(x)

• 步骤二：AdaBoost反复学习基本分类器，在每一轮m=1,2,…,M 顺次的执行下列操作：

  • （a） 在权值分布为Dt的训练数据上，确定基分类器；

  • （b） 计算该学习器在训练数据中的错误率：
    $$\epsilon t=P(ht(xt)\ne yt)$$

  • （c） 计算该学习器的投票权重：

    

  • （d） 根据投票权重，对训练数据重新赋权

    • 将下一轮学习器的注意力集中在错误数据上

  • 重复执行a到d步，m次；

• 步骤三：对m个学习器进行加权投票

  

4.2 关键点剖析

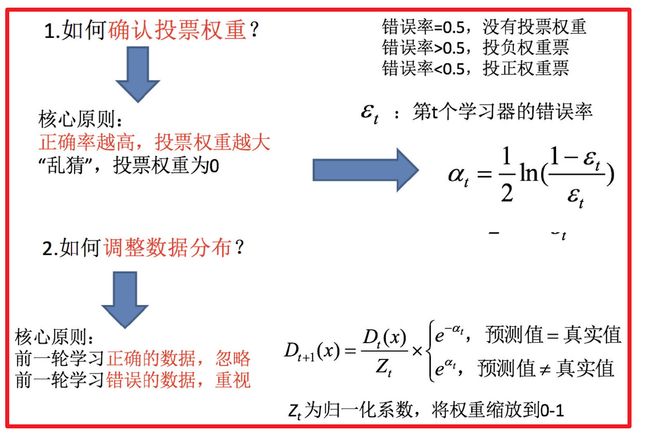
如何确认投票权重？

如何调整数据分布？

4.3 案例介绍

给定下面这张训练数据表所示的数据，假设弱分类器由xv产生，其阈值v使该分类器在训练数据集上的分类误差率最低，试用Adaboost算法学习一个强分类器。

问题解答：

步骤一：初始化训练数据权重相等，训练第一个学习器：
$$D1=(w11,w12,...,w110,)$$

$$w1i=0.1,i=1,2,...,10$$

---

步骤二：AdaBoost反复学习基本分类器，在每一轮m=1,2,…,M顺次的执行下列操作：

当m=1的时候：

（a）在权值分布为D1的训练数据上，阈值v取2.5时分类误差率最低，故基本分类器为:

6,7,8被分错

（b）计算该学习器在训练数据中的错误率：
$$\epsilon 1=P(h1(x1)\ne y1)=0.3$$
（c）计算该学习器的投票权重：

（d）根据投票权重，对训练数据重新赋权:
$$D2=(w21,w22,...,w210,)$$
根据下公式，计算各个权重值

经计算得，D2的值为：
$$D2=(0.07143,0.07143,0.07143,0.07143,0.07143,0.07143,0.16667,0.16667,0.16667,0.07143)$$
计算过程：

H_1(x)=sign[0.4236h_1(x)]H1(x)=sig**n[0.4236h1(x)]

分类器H1(x)在训练数据集上有3个误分类点。

---

当m=2的时候：

（a）在权值分布为D2的训练数据上，阈值v取8.5时分类误差率最低，故基本分类器为:

3,4,5被分错

（b）计算该学习器在训练数据中的错误率：
$${\epsilon }_2=P(h_2(x_2)\ne y_2)=0.2143$$
（c）计算该学习器的投票权重：

（d）根据投票权重，对训练数据重新赋权:

经计算得，D3的值为：
$$D3=(0.0455,0.0455,0.0455,0.1667,0.1667,0.1667,0.1060,0.1060,0.1060,0.0455)$$

$$H2(x)=sign[0.4236h1(x)+0.6496h2(x)]$$

分类器H2(x)在训练数据集上有3个误分类点。

---

当m=3的时候：

（a）在权值分布为D3的训练数据上，阈值v取5.5时分类误差率最低，故基本分类器为:

（b）计算该学习器在训练数据中的错误率：
$${\epsilon }_3=0.1820$$
（c）计算该学习器的投票权重：
$$\alpha 3=0.7514$$
（d）根据投票权重，对训练数据重新赋权:

经计算得，D2的值为：
$$D4=(0.125,0.125,0.125,0.102,0.102,0.102,0.065,0.065,0.065,0.125)$$

$$H3(x)=sign[0.4236h1(x)+0.6496h2(x)+0.7514h3(x)]$$

分类器H3(x)在训练数据集上的误分类点个数为0。

---

步骤三：对m个学习器进行加权投票,获取最终分类器
$$H3(x)=sign[0.4236h1(x)+0.6496h2(x)+0.7514h3(x)]$$

4.4 api

• from sklearn.ensemble import AdaBoostClassifier
  • api链接:https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostClassifier.html#sklearn.ensemble.AdaBoostClassifier

---

5 小结

• 什么是Boosting 【知道】
  • 随着学习的积累从弱到强
  • 代表算法：Adaboost，GBDT，XGBoost，LightGBM
• bagging和boosting的区别【知道】
  • 区别一:数据方面
    • Bagging：对数据进行采样训练；
    • Boosting：根据前一轮学习结果调整数据的重要性。
  • 区别二:投票方面
    • Bagging：所有学习器平权投票；
    • Boosting：对学习器进行加权投票。
  • 区别三:学习顺序
    • Bagging的学习是并行的，每个学习器没有依赖关系；
    • Boosting学习是串行，学习有先后顺序。
  • 区别四:主要作用
    • Bagging主要用于提高泛化性能（解决过拟合，也可以说降低方差）
    • Boosting主要用于提高训练精度 （解决欠拟合，也可以说降低偏差）
• AdaBoost构造过程【知道】
  • 步骤一：初始化训练数据权重相等，训练第一个学习器;
  • 步骤二：AdaBoost反复学习基本分类器;
  • 步骤三：对m个学习器进行加权投票

5.5 GBDT介绍

学习目标

• 知道GBDT的算法原理

---

GBDT 的全称是 Gradient Boosting Decision Tree，梯度提升树，在传统机器学习算法中，GBDT算的上TOP3的算法。

想要理解GBDT的真正意义，那就必须理解GBDT中的Gradient Boosting 和Decision Tree分别是什么？

1 CART回归树

首先，GBDT使用的决策树是CART回归树，无论是处理回归问题还是二分类以及多分类，GBDT使用的决策树通通都是都是CART回归树。

• 为什么不用CART分类树呢？
  • 因为GBDT每次迭代要拟合的是梯度值，是连续值所以要用回归树。

对于回归树算法来说最重要的是寻找最佳的划分点，那么回归树中的可划分点包含了所有特征的所有可取的值。

在分类树中最佳划分点的判别标准是熵或者基尼系数，都是用纯度来衡量的，但是在回归树中的样本标签是连续数值，所以再使用熵之类的指标不再合适，取而代之的是平方误差，它能很好的评判拟合程度。

1.1 回归树生成算法（复习）

• 输入：训练数据集D:
• 输出：回归树f(x).
• 在训练数据集所在的输入空间中，递归的将每个区域划分为两个子区域并决定每个子区域上的输出值，构建二叉决策树：
  • （1）选择最优切分特征j与切分点s，求解遍历特征j,对固定的切分特征j扫描切分点s,选择使得上式达到最小值的对 (j,s).
  • （2）用选定的对(j,s)划分区域并决定相应的输出值：
  • （3）继续对两个子区域调用步骤（1）和（2），直至满足停止条件。
  • （4）将输入空间划分为M个区域R1,R2,……,Rm, 生成决策树：

2 拟合负梯度

梯度提升树（Grandient Boosting）是提升树（Boosting Tree）的一种改进算法，所以在讲梯度提升树之前先来说一下提升树。

先来个通俗理解：假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。最后将每次拟合的岁数加起来便是模型输出的结果。

提升树算法：

• （1）初始化:
  $$f0(x)=0$$

• （2）对m=1,2,…,M

  • （a）计算残差
    $$:r_{mi}=y_i-f_{m-1}(x),i=1,2,...,N$$

  • （b）拟合残差rmi 学习一个回归树，得到
    $$hm(x)$$

    • （c）更新：
      $$f_m(x)=f_{m-1}+h_m(x)$$

• （3）得到回归问题提升树：
  $$f_M(x)=\sum _{m=1}^M{h}_m(x)(x)$$

---

上面伪代码中的残差是什么？

在提升树算法中，

• 假设我们前一轮迭代得到的强学习器是：
  $$f_{t-1}(x)$$

• 损失函数是：
  $$L(y,ft-1(x))$$

• 我们本轮迭代的目标是找到一个弱学习器：
  $$h_t(x)$$

• 最小化让本轮的损失：
  $$L(y,f_t(x))=L(y,f_{t-1}(x)+h_t(x))$$

• 当采用平方损失函数时：

• 这里，是当前模型拟合数据的残差（residual）。
• 所以，对于提升树来说只需要简单地拟合当前模型的残差。

回到我们上面讲的那个通俗易懂的例子中，第一次迭代的残差是10岁，第二 次残差4岁,

---

当损失函数是平方损失和指数损失函数时，梯度提升树每一步优化是很简单的，但是对于一般损失函数而言，往往每一步优化起来不那么容易。

针对这一问题，Friedman提出了梯度提升树算法，这是利用最速下降的近似方法，其关键是利用损失函数的负梯度作为提升树算法中的残差的近似值。

那么负梯度长什么样呢？

• 第t轮的第i个样本的损失函数的负梯度为：

• 此时不同的损失函数将会得到不同的负梯度，如果选择平方损失：

• 负梯度为：

此时我们发现GBDT的负梯度就是残差，所以说对于回归问题，我们要拟合的就是残差。

那么对于分类问题呢？

• 二分类和多分类的损失函数都是logloss。

本文以回归问题为例进行讲解。

3 GBDT算法原理

上面两节分别将Decision Tree和Gradient Boosting介绍完了，下面将这两部分组合在一起就是我们的GBDT了。

---

GBDT算法：

• （1）初始化弱学习器

• （2）对m=1,2,…,M有：

  • （a）对每个样本i=1,2,…,N，计算负梯度，即残差
  • （b）将上步得到的残差作为样本新的真实值，并将数据(x_i,r_{im}), i=1,2,…N(x**i,rim),i=1,2,…N作为下棵树的训练数据，得到一颗新的回归树fm(x)其对应的叶子节点区域为R_{jm}, j =1,2,…, JRjm,j=1,2,…,J 其中J为回归树t的叶子节点的个数。
  • （c）对叶子区域j=1,2,…J计算最佳拟合值
  • （d）更新强学习器

• （3）得到最终学习器

4 实例介绍

4.1 数据介绍

根据如下数据，预测最后一个样本的身高。

编号	年龄(岁)	体重（kg）	身高(m)(标签值)
0	5	20	1.1
1	7	30	1.3
2	21	70	1.7
3	30	60	1.8
4(要预测的)	25	65	？

4.2 模型训练

4.2.1 设置参数：

• 学习率：learning_rate=0.1
• 迭代次数：n_trees=5
• 树的深度：max_depth=3

4.2.2 开始训练

（1）初始化弱学习器:

损失函数为平方损失，因为平方损失函数是一个凸函数，直接求导，倒数等于零，得到c。

令导数等于0

所以初始化时，c取值为所有训练样本标签值的均值。
$$c=(1.1+1.3+1.7+1.8)/4=1.475$$
此时得到初始学习器f0(x)：
$$f0(x)=c=1.475$$
（2）对迭代轮数m=1,2,…,M:

由于我们设置了迭代次数：n_trees=5，这里的M=5。

计算负梯度，根据上文损失函数为平方损失时，负梯度就是残差，再直白一点就是 y与上一轮得到的学习器fm-1的差值：

残差在下表列出：

编号	真实值	f*0(*x)	残差
0	1.1	1.475	-0.375
1	1.3	1.475	-0.175
2	1.7	1.475	0.225
3	1.8	1.475	0.325

此时将残差作为样本的真实值来训练弱学习器f1(x)，即下表数据

编号	年龄(岁)	体重（kg）	标签值
0	5	20	-0.375
1	7	30	-0.175
2	21	70	0.225
3	30	60	0.325

接着，寻找回归树的最佳划分节点，遍历每个特征的每个可能取值。

从年龄特征的5开始，到体重特征的70结束，分别计算分裂后两组数据的平方损失（Square Error），

SEl左节点平方损失，SEr右节点平方损失，找到使平方损失和:
$$SEsum=SEl+SEr$$
最小的那个划分节点，即为最佳划分节点。

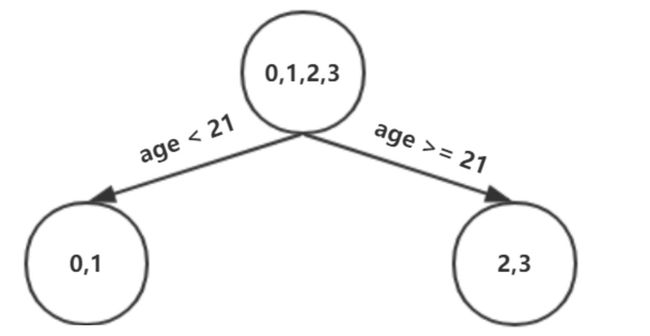
例如：以年龄21为划分节点，将小于21的样本划分为到左节点，大于等于21的样本划分为右节点。左节点包括x0, x1 ，右节点包括样本x2, x3，
$$SEl=0.02,SEr=0.005,SEsum=0.025,$$

$$SEl=[-0.375-(-0.275)]2+[-0.175-(-0.275)]2=0.02$$

$$SEr=[0.225-0.275]2+[0.325-0.275]2=0.005$$

所有可能划分情况如下表所示：
|

以上划分点是的总平方损失最小为0.025有两个划分点：年龄21和体重60，所以随机选一个作为划分点，这里我们选 年龄21 现在我们的第一棵树长这个样子：

我们设置的参数中树的深度max_depth=3，现在树的深度只有2，需要再进行一次划分，这次划分要对左右两个节点分别进行划分：

---

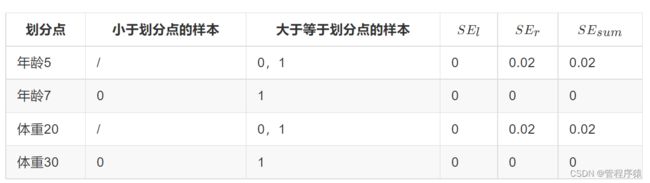
对于左节点，只含有0,1两个样本，根据下表我们选择年龄7划分

划分点	小于划分点的样本	大于等于划分点的样本	SE_lSEl	SE_rSEr	SE_{sum}SEsum
年龄5	/	0，1	0	0.02	0.02
年龄7	0	1	0	0	0
体重20	/	0，1	0	0.02	0.02
体重30	0	1	0	0	0

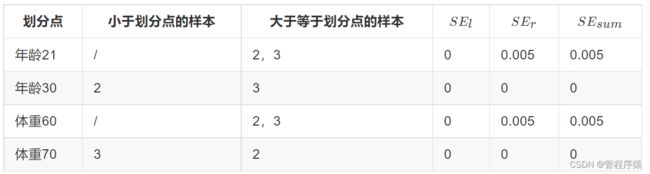
对于右节点，只含有2,3两个样本，根据下表我们选择年龄30划分（也可以选体重70）

划分点	小于划分点的样本	大于等于划分点的样本	SE_lSEl	SE_rSEr	SE_{sum}SEsum
年龄21	/	2，3	0	0.005	0.005
年龄30	2	3	0	0	0
体重60	/	2，3	0	0.005	0.005
体重70	3	2	0	0	0

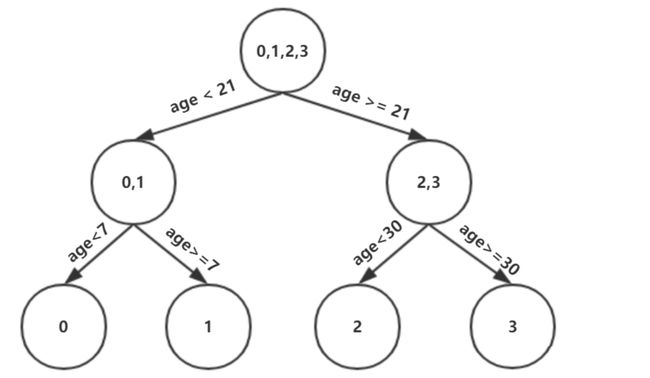
现在我们的第一棵树长这个样子：

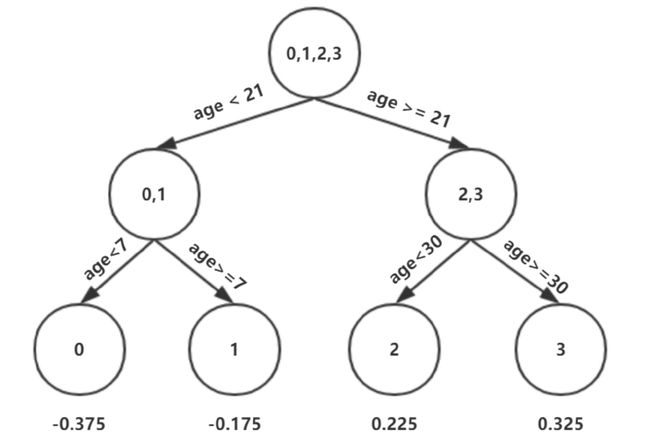
此时我们的树深度满足了设置，还需要做一件事情，给这每个叶子节点分别赋一个参数 r ，来拟合残差。

这里其实和上面初始化学习器是一个道理，平方损失，求导，令导数等于零，化简之后得到每个叶子节点的参数 r ，其实就是标签值的均值。这个地方的标签值不是原始的 y，而是本轮要拟合的标残差 y - f0(x).

根据上述划分结果，为了方便表示，规定从左到右为第1,2,3,4个叶子结点

此时的树长这个样子：

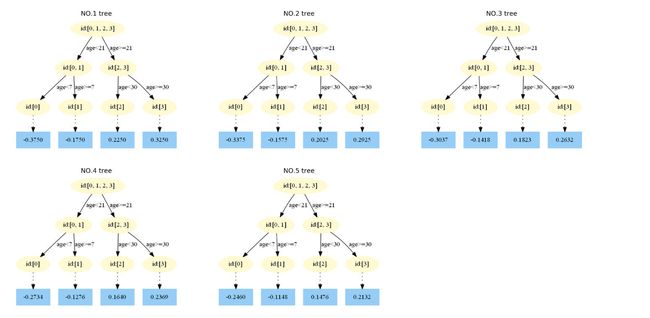
此时可更新强学习器，需要用到参数学习率：learning_rate=0.1，用 lr 表示。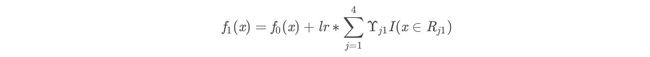

为什么要用学习率呢？这是Shrinkage的思想，如果每次都全部加上（学习率为1）很容易一步学到位导致过拟合。

重复此步骤，直到 m>5 结束，最后生成5棵树。

结果中，0.9倍这个现象，和其学习率有关。这是因为数据简单每棵树长得一样，导致每一颗树的拟合效果一样，而每棵树都只学上一棵树残差的0.1倍，导致这颗树只能拟合剩余0.9了。

（3）得到最后的强学习器：

（4）预测样本：

• f_0(x)=1.475f0(x)=1.475
• 在f1(x)中，样本4的年龄为25，大于划分节点21岁，又小于30岁，所以被预测为0.2250;
• 在f2(x)中，样本4的…此处省略…所以被预测为0.2025;
• 在f3(x)中，样本4的…此处省略…所以被预测为0.1823;
• 在f3(x)中，样本4的…此处省略…所以被预测为0.1640;
• 在f5(x)中，样本4的…此处省略…所以被预测为0.1476.

最终预测结果：
$$f(x)=1.475+0.1\ast (0.225+0.2025+0.1823+0.164+0.1476)=1.56714$$

---

5 小结

GBDT算法原理【知道】

• （1）初始化弱学习器

• （2）对m=1,2,…,M有：

  • （a）对每个样本i=1,2,…,N，计算负梯度，即残差

  • （b）将上步得到的残差作为样本新的真实值，并将数据
    $$(xi,rim),i=1,2,..N$$
    作为下棵树的训练数据，得到一颗新的回归树fm(x)其对应的叶子节点区域为
    $$Rjm,j=1,2,...,J$$
    其中J为回归树t的叶子节点的个数。

  • （c）对叶子区域j=1,2,…J计算最佳拟合值

  • （d）更新强学习器

…(img-MzcO5A5j-1667053529812)]

结果中，0.9倍这个现象，和其学习率有关。这是因为数据简单每棵树长得一样，导致每一颗树的拟合效果一样，而每棵树都只学上一棵树残差的0.1倍，导致这颗树只能拟合剩余0.9了。

（3）得到最后的强学习器：

[外链图片转存中…(img-Key532hz-1667053529812)]

（4）预测样本：

• f_0(x)=1.475f0(x)=1.475
• 在f1(x)中，样本4的年龄为25，大于划分节点21岁，又小于30岁，所以被预测为0.2250;
• 在f2(x)中，样本4的…此处省略…所以被预测为0.2025;
• 在f3(x)中，样本4的…此处省略…所以被预测为0.1823;
• 在f3(x)中，样本4的…此处省略…所以被预测为0.1640;
• 在f5(x)中，样本4的…此处省略…所以被预测为0.1476.

最终预测结果：
$$f(x)=1.475+0.1\ast (0.225+0.2025+0.1823+0.164+0.1476)=1.56714$$

---

5 小结

GBDT算法原理【知道】

• （1）初始化弱学习器[外链图片转存中…(img-Ua3dbsNF-1667053529813)]

• （2）对m=1,2,…,M有：

  • （a）对每个样本i=1,2,…,N，计算负梯度，即残差[外链图片转存中…(img-gdBav0QZ-1667053529813)]

  • （b）将上步得到的残差作为样本新的真实值，并将数据
    $$(xi,rim),i=1,2,..N$$
    作为下棵树的训练数据，得到一颗新的回归树fm(x)其对应的叶子节点区域为
    $$Rjm,j=1,2,...,J$$
    其中J为回归树t的叶子节点的个数。

  • （c）对叶子区域j=1,2,…J计算最佳拟合值[外链图片转存中…(img-XejKn5B3-1667053529813)]

  • （d）更新强学习器[外链图片转存中…(img-HjZFtq8Z-1667053529814)]

• （3）得到最终学习器