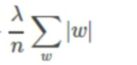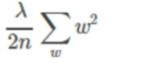BP神经网络算法
1.简单介绍
人工神经网络,实际上就是每一层的输出作为下一层的输入,建立起一层一层的神经元,通过不断优化大量的W和b(如何优化是BP算法的重点),无限去拟合样本数据,神经网络十分强大,可以处理十分复杂的数据。在输出之前,还要通过激励函数对zLi进行非线性处理得到aLi,如果不处理,每层的输出就都是关于输入值的一个线性组合,此时就相当于与多元线性回归模型了,将不能处理复杂的非线性可分问题。如下图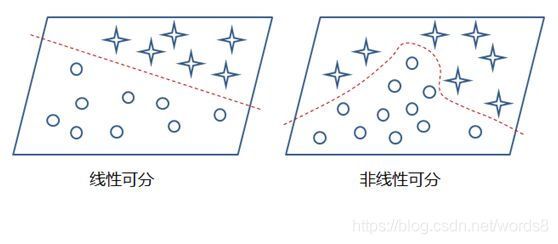
1. 神经元
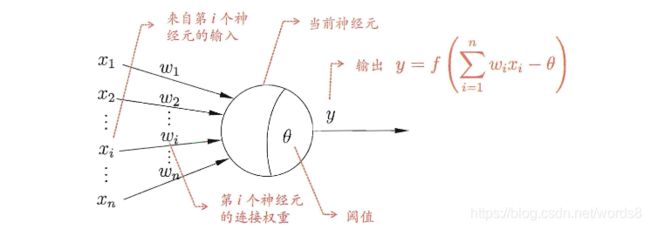
神经网络中最简单的模型就是神经元模型(MP-神经元模型)了,利用人工方法模拟生物神经元而形成的模型。多输入、单输出。如下图,x1 , x2 , … , xn,表示来自多个神经元的输入;w1 , w2 , … , wn,表示对于的权重,正好模拟了生物神经元的兴奋和抑制的效果;之后将x和w相乘并求和再减去一个阈值,(感觉这里的阈值和线性回归中的b类似)将得到的结果用神经元进行处理;这里的处理就是利用上面说到的激励函数进行函数的复合运算,最终得到y。最开始MP-神经元模型的激励函数非常的简单,sgn(阶跃)函数,其实就是y>=0时,输出为1,y<0时,输出0。MP-神经元模型
2. 感知机
感知机是由两层的神经元组成,第一层作为输入层,x1 , x2 , … , xn,第二层作为输出层,这里的输出层由多个神经元组成,只对输出层进行激励函数处理。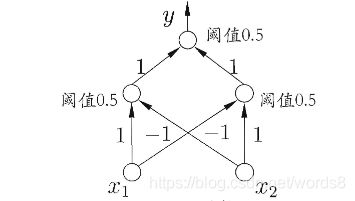
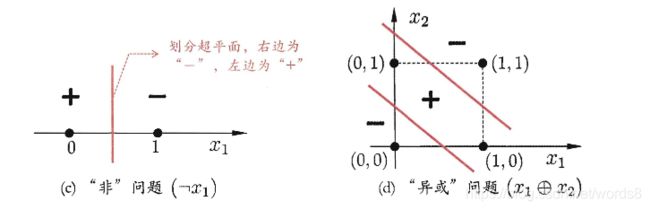
感知机依旧是一个二分模型(取1或-1),且只能解决线性分类,一个线性超平面能将两类模式分开。如下图,可以解决线性可分的‘非’问题,不能解决非线性可分的‘异或‘问题。这里就不再进行具体描述了。
3. 多层前馈神经网络
感知机只有一层功能神经层过于简单只能处理线性可分的问题,但我们再加一些功能层就可以解决非线性可分问题,这个是有数学证明的。
先上一个图
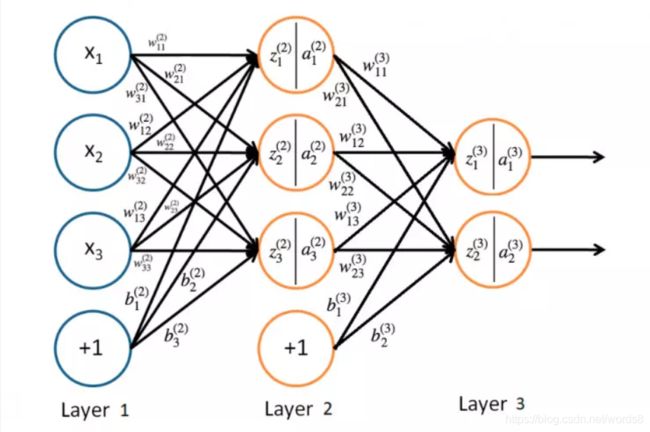
1. Layer1为输入层,x1,x2,x3表示一个样本里的每个特征;
2. Layer2为隐藏层(功能层)当然隐藏层可以不止一层,在神经网络中输入层与输出层之间的层称为隐含层或隐层,
隐层和输出层的神经元都是具有激活函数的功能神经元;
3. Layer3为输出层,输出值更大的对于类别作为预测label。
BP神经网络是一种多层前馈神经网络
多层前馈神经网络结构有以下特点:
- 每层神经元与下一层神经元之间完全互连
- 神经元之间不存在同层连接
- 神经元之间不存在跨层连接
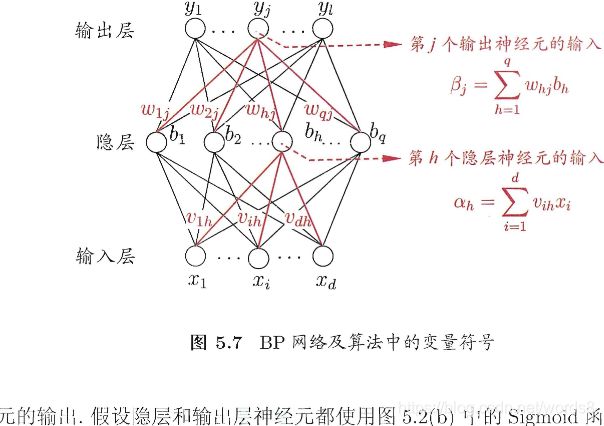
wLij中,L表示第几层,i表示第L层第i个神经元,j表示第L层第i个神经元的第j个权重。每层的所有神经元与下一层每个神经元的都有一个权重,下一层的值也就是这里的zLi是上一层输入的每个值和与每个zLi相对应得WL相乘累加再加上阈值b得到zLi,再进行激励函数处理得到的aLi。
比如z21 = x1*W211 + x2*W212 + x3*W213 +x4*W214 + b21
2. 算法概要
这里以一层隐含层为例
1. 初始化w,b。
首先往往要先设置一下超参数:输入层维度:n_input ;隐含层维度:n_hide; 输出层维度:n_output;学习率等。
输入层没有参数,从第二层开始。都是二维数组,这里自己随机取值,可以有很多种取法
W1 = np.random.randn(n_input, n_hide)
b1 = np.zeros((1,n_hide))
W2 = np.random.randn(n_hide, n_output)
b2 = np.zeros((1,n_output))
2. 向前传播计算
- 利用输入的数据x1,x2,…和w,b的二维数组巧妙地进行矩阵运算从前往后得到每一个神经元的z。当然第一层是不用算的,也可以把第一层的z看做是输入的x。
- 激励函数非线性化变换
在把z传入到下层前进行激励函数处理,实际上就是进行函数的复合运算
a = f(z),激励函数有很多种,sigmoid函数,tanh函数, softmax函数等等,根据实际情况选择激励函数。
激励函数可不是随意找个的,必须要可导或大部分可导,单调且非线性,后面求梯度时会用到。
sigmoid(x):sigmoid(x)把函数值都压缩到了(0,1)之间 ,导数为 sigmoid(x) *(sigmoid(x) - 1)
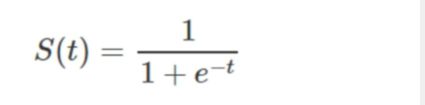
tanh(x):tanh(x)把函数值都压缩到了(-1,1)之间,导数为 (1 - tanh(x)2)

softmax

前面两个好理解,直接将每个z带入得到a,而softmax,ej表示输出层的前一层,也就是第二层每个z的ez,进行求和,将每个ez除于和得到a,此时,每个a都在(0,1)之间,累加为1,恰好和概率套上了。进行矩阵运算、激励函数处理,向前传播结束
3. 向后传播误差
这一步是BP的核心,参数优化往往通过梯度下降法来最小化loss函数来求解,进行loss最小化,如果直接进行求偏导,是很难求的,BP算法是从输出层开始梯度求解,注意,每层之间实际上都是进行一个函数复合以后得到的,所以只要求出最后一层,就可以一层一层地往前面推,得到每层的梯度。有人问了,不能从中间和前面?这样子似乎弄不太出来!
(梯度下降这里就不具体介绍了,当做你已经知道了)
1. 我们就先用常用的均方误差:
ok,梯度求出来了(其实吧,我觉得倒数第二层都求出来了,也就是这里唯一的隐藏层,如果还有隐藏层,梯度就等于上一隐藏层的g*w再乘该层激励函数的导数乘该层的输入),然后进行更新
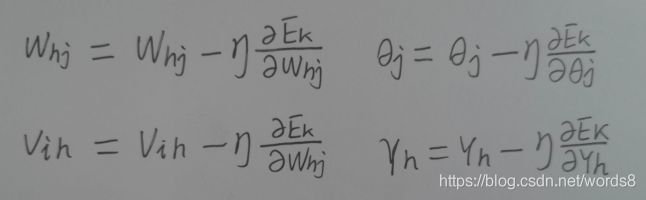
注意!!!上面的公式都是求一个参数的,我们是想一个样本全部更新一次的,所以算的时候进行运算的应该是向量和矩阵 ,太方便了!!!如果用循环取求每个参数代码多,效率还低。
2.再使用log_likelihood交叉熵损失
loss = - lnay,ay表示一个训练样本的真实label在输出层所对应的概率,我们要想模型训练的好,那自然希望ay越大越好,甚至为1,对ay取对数的相反数,此时,ay与loss成反比,即要求ay最大,只要使loss最小即可。真正求loss值时,会有很多个样本,要将所有的loss相加得到最总的损失。
梯度公式
dW2 = a(2)T * (ay-1)
db2 = (ay-1)
dw1 = (ay-1) * XT * (W(3)T) * f(a1)’
db1 = (ay-1) * (W(3)T) * f(a1)’
这个就不推了,其实不难发现前面的梯度和这里的很有相似度,想具体了解的话可以点这 推导
然后进行梯度下降W,b更新:
W2 -= epsilon * dW2
b2 -= epsilon * db2
W1 -= epsilon * dW1
b1 -= epsilon * db1
3.算法实现
1.loss是均方误差
导入包
import numpy as np
import random
from sklearn.datasets import load_digits
用的激励函数是sigmoid(也用过tanh,效果不好,可能是因为取到了负值,导致loss有些小的平方后变大)
def sigmoid(x): #支持数组和数字
return 1. / (1 + np.exp(-x))
def sigmoid_d(x): #导数
return x * (1 - x)
自己实现算法
class NeuralNetworkBP:
def __init__(self,n_input,n_hide,n_output,losslim=1.5,epsilon=0.1,nums=20000):
self.n_input = n_input
self.n_hide = n_hide
self.n_output = n_output
self.epsilon = epsilon #学习率
self.losslim = losslim #loss的min
self.nums = nums #参数更新次数上限
self.W1 = np.random.random((n_input,n_hide))*2-1#初始化
self.b1 = np.ones((1,n_hide))
self.W2 = np.random.random((n_hide,n_output))*2-1
self.b2 = np.ones((1,n_output))
def forward(self,x): #一个或多个样本
z1 = (np.dot(x,self.W1) + self.b1)
a1 = sigmoid(z1)
z2 = (np.dot(a1,self.W2) + self.b2)
a2 = sigmoid(z2)
return a1,a2
def loss(self,X,y):
a1, a2 = self.forward(X)
loss = np.sum((a2 - y)**2)/len(a2)
return loss
def backward(self,X,Y):
a = []
for k in range(self.nums + 1):
i =np.random.randint(X.shape[0]) #随机取样本
a.append(i)
x = X[i].reshape((1,-1))
y = Y[i]
a1, a2 = self.forward(x) #向前传播
#前面推的公式是针对一个参数的,我们可以用向量和矩阵来很好地简化运算!!
#一个样本更新全部参数一次 注意下面是向量相乘 还有矩阵相乘
delta2 = (a2 - y) * sigmoid_d(a2)
dW2 = np.dot(a1.T,delta2)
db2 = -delta2
delta1 = np.dot(self.W2,delta2.T).T * sigmoid_d(a1)
dW1 = np.dot(x.T,delta1)
db1 = -delta1
self.W2 -= self.epsilon*dW2
self.b2 -= self.epsilon*db2
self.W1 -= self.epsilon*dW1
self.b1 -= self.epsilon*db1
if k % 1000 == 0:
loss = self.loss(X,Y)
#可以考虑每经过一段时间进行对学习率小小调整
print(k,self.nums,loss)
if loss < self.losslim:
break
def fit_bp(self,X_train,y_train):
#对y_train进行one_hot处理
Len_X = len(X_train)
y = np.zeros((Len_X,len(set(y_train))))
for i in range(Len_X):
y[i,y_train[i]] = 1
#梯度下降 参数优化
self.backward(X_train,y)
return self
def predict(self,X,y):
a1, a2 = self.forward(X)
pre = np.argmax(a2,axis=1)
print('accuracy_score: {0}/{1} {2}'.format(np.sum(pre==y),len(y),np.sum(pre==y)/len(y)))
return pre
测试
digits=load_digits()#载入手写数字数据
X=digits.data#数据
y=digits.target#标签
#数据归一化,一般是x=(x-x.min)/x.max-x.min
#X-=X.min()
#X/=X.max()
#创建神经网络
def train_test_split(x,y,rate=0.3):
indexs = np.array(range(0,len(x)))
random.shuffle(indexs) #打乱索引
n = len(x) - int(rate*len(x))#train的数据量
x_train, x_test, y_train, y_test = x[indexs[:n]], x[indexs[n:]], y[indexs[:n]], y[indexs[n:]]
return x_train, x_test, y_train, y_test
X_train,X_test,y_train,y_test=train_test_split(X,y)
hhh=NeuralNetworkBP(n_input=64,n_hide=100,n_output=10,losslim=0.05,epsilon=0.1,nums=20000)
hhh.fit_bp(X_train,y_train)
print('预测测试集:')
pre = hhh.predict(X_test,y_test)
结果
0 20000 4.265594388782199
1000 20000 0.5640010225933353
2000 20000 0.37535017658211084
3000 20000 0.3235283530723675
4000 20000 0.27962917536299936
5000 20000 0.26878928000224817
6000 20000 0.21609324912562317
7000 20000 0.20227565346750254
8000 20000 0.2132084917358956
9000 20000 0.1812052450583217
10000 20000 0.09539378212335196
11000 20000 0.09655858802300703
12000 20000 0.07185631080618225
13000 20000 0.06691750710629663
14000 20000 0.059483413989111306
15000 20000 0.07558515504417504
16000 20000 0.054753356456327854
17000 20000 0.0570280171718812
18000 20000 0.04184277224603063
预测测试集:
accuracy_score: 512/539 0.9499072356215214
刚开始时吧,效果不算很好,以为是学习率和神经元个数的问题,调了很久没什么用,后来注意到一篇文章里对参数初始化的操作,里面不像我刚开始就用np.random.randn()函数生成服从标准正太分布的随机数,所以我就改了下,结果预测结果居然更稳定了,效果也更好了!!
学习率大小、参数如何初始化、神经元个数都会影响结果
2.loss是log_likelihood交叉熵
import numpy as np
from sklearn import datasets
import random
#一层隐含层的BP算法
class BP:
#超参数有:输入层维度 隐层维度 输出层维度 学习率 losslim 正则化参数
def __init__(self,n_input,n_hide,n_output,losslim=0.001,epsilon=0.01,reg=0):
self.n_input = n_input
self.n_hide = n_hide
self.n_output = n_output
self.epsilon = epsilon
self.losslim = losslim
self.reg = reg
self.W1 = None
self.b1 = None
self.W2 = None
self.b2 = None
def loss(self, X, y):
Len_X = len(X) #一个训练样本的大小
z1 = X.dot(self.W1) + self.b1
a1 = np.tanh(z1)
z2 = a1.dot(self.W2) + self.b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) #概率为0到1
#计算loss 取每个样本真实类别的概率的负值
corect_logprobs = -np.log(probs[range(Len_X), y])
data_loss = np.sum(corect_logprobs)
#loss正则化
data_loss += self.reg / 2 /len(X)* (np.sum(np.square(self.W1)) + np.sum(np.square(self.W1)))
return 1. / Len_X * data_loss
#nums:最多迭代次数
def fit_bp(self,X,y,nums=10000):
#初始化参数
W1 = np.random.randn(self.n_input, self.n_hide)
b1 = np.zeros((1,self.n_hide))
W2 = np.random.randn(self.n_hide, self.n_output)
b2 = np.zeros((1,self.n_output))
lenth_X = len(X)
#反向传播 梯度下降优化参数
for i in range(0,nums):
#前传播
z1 = np.dot(X,W1) + b1
a1 = np.tanh(z1)
z2 = np.dot(a1,W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
#求梯度
delta2 = probs
delta2[range(lenth_X), y] -= 1 #找出X_train真实标记的概率,再算导数
dW2 = np.dot(a1.T,delta2) #50 1
db2 = np.sum(delta2, axis=0)
delta1 = delta2.dot(W2.T)*(1-np.power(a1,2))#np.power求平方效率更高
dW1 = np.dot(X.T,delta1)
db1 = np.sum(delta1, axis=0)
dW2 += self.reg * W2 / len(X)#正则化 防止过拟合
dW1 += self.reg * W1 / len(X)
W1 += -self.epsilon * dW1
b1 += -self.epsilon * db1
W2 += -self.epsilon * dW2
b2 += -self.epsilon * db2
self.W1 = W1
self.b1 = b1
self.W2 = W2
self.b2 = b2
if i % 100 == 0: #打印loss的变化过程
print('loss is ({0},{1}): {2}'.format(i,nums,self.loss(X,y)))
if self.loss(X,y) < self.losslim:
return self
return self
def predict(self,x):
z1 = x.dot(self.W1) + self.b1
a1 = np.tanh(z1)
z2 = a1.dot(self.W2) + self.b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
#keepdims保持二维特征 进行矩阵运算
return np.argmax(probs,axis=1)
iris = datasets.load_iris()
X = iris.data
y = iris.target
def train_test_split(x,y,rate=0.25):
indexs = np.array(range(0,len(x)))
random.shuffle(indexs) #打乱索引
n = len(x) - int(rate*len(x))#train的数据量
x_train, x_test, y_train, y_test = x[indexs[:n]], x[indexs[n:]], y[indexs[:n]], y[indexs[n:]]
return x_train, x_test, y_train, y_test
x_train, x_test, y_train, y_test = train_test_split(X,y)
model = BP(n_input=4,n_hide=10,n_output=3,losslim=0.01,epsilon=0.001,reg=0.1)
model.fit_bp(x_train,y_train,nums=1000)
pre = model.predict(x_test)
print(np.sum(pre==y_test),len(y_test),np.sum(pre==y_test)/len(y_test))
运行结果
loss is (0,1000): 2.658971325180942
loss is (100,1000): 0.5308237863773526
loss is (200,1000): 0.50165261631469
loss is (300,1000): 0.29074533794257196
loss is (400,1000): 0.16833186847475642
loss is (500,1000): 0.1345514320283633
loss is (600,1000): 0.11225017916856792
loss is (700,1000): 0.1028605363492959
loss is (800,1000): 0.09690664636582166
loss is (900,1000): 0.09228574257942757
36 37 0.972972972972973
4.小结
程序进行多次运行发现,第二个程序少数情况下出现了准确率只有0.3,这是为什么?这是因为梯度优化参数的时候得到局部最优解导致结果不准确;还有可能过拟合了,所以上面进行了正则化处理过拟合,不过这个数据集效果没有那么明显。先到这里吧,有什么不对欢迎指正
这里再简单介绍一下过拟合
-
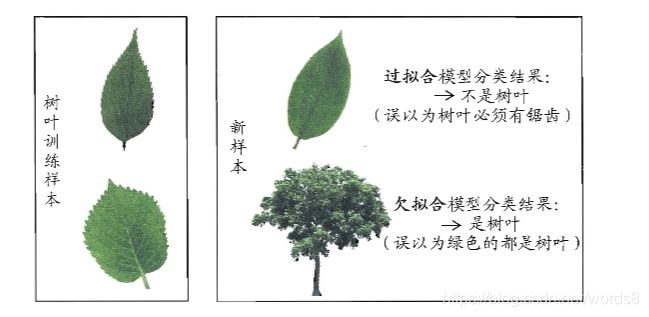
过拟合:训练时模型学的太好了,很可能已经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质,过于严格这样就会导致泛化性能下降。
-
现象:过拟合会导致有时在神经网络模型训练时误差已经很小了,在训练集上表现的非常优秀,但在测试阶段误差却飙升。
-
导致过拟合的因素:训练数据量太小;数据有噪音;训练过度导致模型非常复杂等。(往往最常见的是因为模型过于复杂)
-
解决方法:增加训练集。对模型过于复杂的问题进行正则化处理,其实就是在loss函数的后面加一个正则化项,防止某些“过于自信”的神经元占据主导地位。
前面的 n表示样本数,另一个为一个系数,一般比较大,因为大了,相对来说w就小了,参数小了模型就更简单化。
欠拟合就跟简单了,模型没有很好的捕捉到数据特征,像神经网络的话,可以添加训练的轮数。
最后再举个西瓜书里一个关于过拟合、欠拟合的形象的例子,是不是很好理解