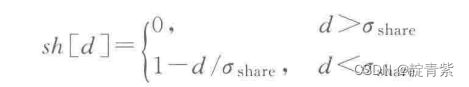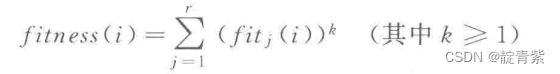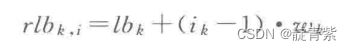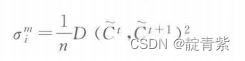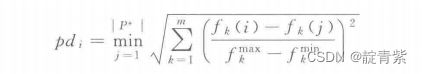多目标优化算法学习笔记
MOEA
分类
按机制分配
基于分解
将子目标聚合成单目标
基于支配
基于Pareto的适应度分配
基于指标
基于指标评价候选解的性能
按决策分类
前决策
搜索前输入决策信息，产生一个解
后决策
提供一组解供决策者选择
independent sampling 每个目标赋予不同权值每次调整
criterion selection 分为k个子种群对不同目标进行优化，非凸函数难以找到最优
aggregation selection 对所取个体适应度进行选择，会丢失边缘解
pareto sampling 基于pareto适应度分配
交互决策
前后都有，效率低，难以定义决策偏好
进一步研究方向
更接近自然的
基于进化环境的
构造多目标最优解的最少时间复杂度
个体循环归档
MOEA参数不同时的比较
非支配解集变化规律
保持分布性
并行
异位显性：某个目标函数依赖其他决策变量
生物激励机制
非支配向量数据结构
多目标处理单目标
测试问题的构造
性能评价标准
高维
高维偏好
约束MOEA
动态MOEA
MOEA应用
优化基础
进化算法
交叉 （取出一对个体交叉位置交换）变异
多目标优化问题
使目标函数达到最优
多目标进化个体间关系
p的所有子目标均优与q，p支配q，p为非支配解，q为支配解。
pareto最优解集
非损人不能利己
从决策空间到目标空间的映射
凸集，任意两点的连线均在集合内
凹集，有两点的连线上的点不在集合内
pareto最优解集构造
构造pareto的简单方法
Deb非支配排序
构造一个一样的集合，将每个个体放入，若被支配则放出，删除所有被他支配的
排除法
构造空集合，每个个体与非支配集每一个比较，若支配其他的其他的排除，若不被任意一个支配则加入
庄家法
庄家法则是一种非回溯的方法，它每次构造新的非支配个体时不需要与已有的非支配个体进行比较，每一轮比较在构造集中选出一个个体出任庄家（一般为当前构造集的第一个个体)，由庄家依次与构造集中其他个体进行比较，并将庄家所支配的个体淘汰出局;一轮比较后，如果庄家个体不被任何其他个体所支配，则庄家个体即为非支配个体，否则庄家个体在该轮比较结束时也被淘汰出局。按照这种方法进行下一轮比较，直至构造集为空。
每次第一个与其他比较.
擂台法
每一轮比较不一定能构造出一个新的非支配个体，每一轮比较时在构造集中选出一个个体出任擂台主，由擂台主与构造集中其他个体进行比较，败者被淘汰出局，胜者成为新的擂台主，并继续该轮比较;一轮比较后，最后的擂台主个体即为非支配个体。按照这种方法进行下一轮比较,直至构造集为空。
胜者与其他比较
递归法
分为两个子集，分治
快速排序
定义新关系
用快速排序的思路实现将非支配集从群体中分类出来。每次找一个个体x作为比较对象（一般选第一个个体)，按照关系“>d”进行比较判断，经一趟排序后，以x为中界将Pop 中的个体分成两部分，比 cx小”的一部在下一轮排序时就不必考虑了;第二部分是比x大的个体或与x不相关的个体，如果x不
被所有这些个体所支配，则x是Pop的非支配个体，将αx并入非支配集中，但只要其中之一“大于”x，则x为被支配个体。如此进行下一轮排序，直至第二部分只有一个个体。
群体的分布性
小生境保持分布
基于干预选择
子个体适应度大于父代个体替代独代个体
基于排挤
设置排挤因子（CF），在进化群体中取1/CF的个体组成的排挤子集，新的个体与排挤子集的相似性，用新的个体代替排挤子集
基于共享
定义共享函数，一个个体的共享度是该个体与其他个体之间共享函数值的总和。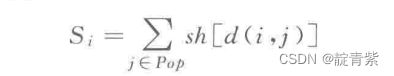
个体共享度是fitness（i）/Si,sh[i,j]为共享函数
计算共享半径内个体相似程度
共享适应度为fitness（i）/m
目标函数组合法
也可以线性组合
容易丢失边界点
简单支配法
n为支配个体i的个体数，对任意个体i适应度为
复合支配关系法
非支配集
n为非支配集的数量 N为种群总数
支配集
信息熵保持分布
q=p/n
分为p个子集，每个子集的均值是种群每个个体的均值
聚集密度法保持分布
相似度计算个体聚集密度
用影响因子计算个体密度
聚集距离计算密集度
p为聚集距离 f为子目标
网格法保持分布
一个网格划分为数个小区域
删除聚集密度大的个体
自适应网络
聚类保持分布
i，j为两个p维向量
欧式距离
曼哈坦距离
明考斯距离
二进制
基于中心聚类
基于类距离的层次聚类
基于类核距离的聚类
极点分析与处理
f达到最优，则为极点
非均匀问题分布性
杂乱度
种群维护
淘汰杂乱度最大的
收敛性
收敛性分析
reduce函数
每次产生一个新个体时，只有当它对归档集是非支配的，才将该个体加入到归档集，并将归档集中被它所支配的所有个体删除
自适应网格算法及其收敛性
多目标进化算法
基于分解的
三类聚合函数
权重聚合
目标函数按权重聚合，不能很好处理pareto为凹的情况
切比雪夫方法
非线性多目标聚合，可以解决非凸问题
基于惩罚的边界交叉方法
基于支配的
分为r个子种群对每个目标进行搜索
NSGA2
在 NSGA-Ⅱ中，将进化群体按支配关系分为若干层，第一层为进化群体的非支配个体集合，第二层为在进化群体中去掉第一层个体后所求得的非支配个体集合，第三层为在进化群体中去掉第一层和第二层个体后所求得的非支配个体集合，依此类推。选择操作首先考虑第一层非支配集，按照某种策略从第一层中选取个体﹔然后再考虑在第二层非支配个体集合中选择个体，依此类推,直至满足新进化群体的大小要求。
个体i的聚集距离
p为在子目标上的目标函数值
r为子目标数量
NPGA
NPGA的主要优点是运行效率比较高，且能获得较好的Pareto最优边界。不足之处是小生境半径的选取与调整比较困难。
随机地从进化群体中选择两个个体i和j，再随机地从进化群体中选取一个比较集CS(其规模大于2，一般约为10)，然后用个体i和个体j分别与CS 中的个体进行比较，如果其中之一受CS 的支配，而另一个个体不受CS支配，那么这个不被CS支配的个体将被选中参与下一代进化。如果个体i和个体j都不受或都受CS支配，则采用共享机制选择共享适应度大的(或小生境计数小的）个体参与下一代进化操作。
适应度共享
d为i和j的距离，sh为共享函数
oshare为小生境半径
SPEA2
个体适应度计算
D中ok为个体i到第k个临近个体的距离
PESA
PAES
若互不支配
MGAMOO
MOMGA
基于信息熵的MOEA
mBOA
贝叶斯网络
基于指标的
Hypervplume
超体积评价指标HV
解集与参考点在目标空间围成的超立方体
二元 indicator
n个目标最小化问题
SMS-EMOA
IBEA
a与b集合互相不支配时合成为一个新集合
高维MOEA
NSGA III
随机产生父代种群，交叉变异产生子代。选择机制构建新的优秀个体，新的优秀个体分为不同的非支配层，定义临界层，采用临界层选择法选择个体。
参考点设置
边界交叉构造权重
每一维度分为p份，M为维度
种群自适应标准化
取每一维最小值构成种群理想点，将种群进行平移（每个个体适应值减去理想点）得到原点，将每一维度极大值取标量函数极小值
w为方向向量，wi在NAGA III中用10的-6次方替代
将极值点构造M维超线性平面，每一维截距为ai
关联操作
参考点设置完后进行关联操作，让种群中的个体分别关联到相应的参考点。将原点与参考点的连线作为该参考点在目标空间中的参考线(如图7.3 中虚线所示)。然后计算Si中的个体到各个参考线的距离，当个体与参考线距离最近则将个体与对应的参考点相关联。图7.3给出了3维目标的图例，其中灰色.点代表参考点，黑色点代表目标空间中的个体，个体分别找到离它最近距离的参考线，然后将它与对应的参考点关联起来。
个体保留操作
找出关联个数最少的参考点，
E-MOEA
归档集B个体所在网格的原点坐标，个体进行支配比较时比较B即可
f为归档集种个体在j维目标最小值，E是允许容忍的偏差，M为目标维度。
第―种情况：Va∈Q，若a E支配c，则个体c将不被Q接收。
第二种情况:Va ∈Q，若c E支配a，则将个体c将加入到Q中,同时删除被c支配的所有个体。
第三种情况:Va∈Q，若c与a互不e支配，且个体c与a在同一个网格中即它们的确定序列B相同，则首先检测 Pareto支配关系，如果个体c支配a,则将个体c加入到Q中，同时删除个体a;如果个体c和a互不支配，但是c更靠近网格原点（根据欧几里得距离)，则将个体c加入到Q中，同时删除个体a。
第四种情况:Va∈Q(t)，若c与a互不E支配，且个体c与a不在同一个网格中,将个体c将加入到Q中。
SDE
基于移动的密度估计策略(shift-based density estimation)
对个体p进行密度估计，比较其他个体与p在每一维目标上的收敛性，如果在这一维目标上某个或某些个体的性能好于个体p，则在这一维目标上将它们移动到个体p所在的位置;否则不变。
N是代表p的大小，dist是相似程度qi’是移动后的个体
偏好MOEA
g-dominance
g-dominace支配，若Flag(a）>Flag(b)或Flag（a）=Flag(b)存在一个j使得aj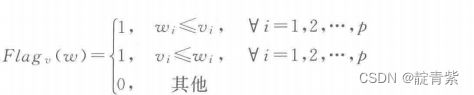
r-dominance
若pareto支配则r支配，
g为参考点
角度信息偏好
个体角度
若pareto支配或两个个体角度的差值在一定范围内则偏好角度支配
偏好聚集距离
同一层的个体距离大的优先选入下一代
动态环境
动态多目标
问题的属性会随时间改变
四种类型
保持种群多样性
超变异策略
随机移民策略
基于记忆的方法
基于归档集的混合记忆
免疫克隆算法
中心点-方差记忆
基于预测的方法
向前预测
基于梯度预测
基于种群预测
多种群策略
动态转静态
固定时间参数
定义静态序值方差和密度方差
FPS
向前预测策略
初始种群由三部分构成，环境变化前的非支配解集，随机产生的解集和预测的解集
记录历史位置，下一个时间步到达或目标函数的变化则预测集合放入进化种群
PPS
基于种群预测
首先将种群分成中心点和副本
中心点评估
副本为
中心点组成一个时间序列用来预测下一个中心点，后者通过前面的副本预测新副本
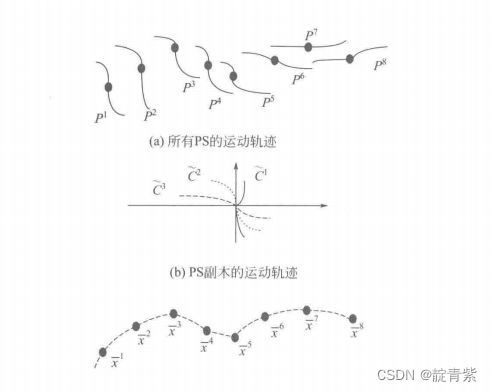
中心点预测
历史中心点带入得到个矩阵
系数向量A
变量用平均平方误差
副本估计
副本A B的距离
下一刻解生成
DEE-PDMS
基于动态环境进化模型的种群多样性保持策略
进化模型的实现
上下边界的计算
div为每一维上单元域数目
k维目标上的域坐标
x为个体，n为维度 Gaussian为标准正态随机数，C为第一层非支配解集的中心点位置。
p是非支配解集的大小
划分子种群
性能评价
设计与分析
1 与已有算法在收敛性、所求解集分布性方面的比较实验。
2 与已有算法在求解能力方面的比较实验。
3 与已有算法在鲁棒性方面的比较实验，如对所求解问题特征的敏感性、对待处理数据质量的敏感性、对不同参数设置的敏感性等。
4 与已有算法在应用范围方面的比较实验。
5 与已有算法在效率上的比较实验。
评价方法
解集质量
所求解集和实际最优值的偏差
计算效率
cpu计算时间或迭代次数
鲁棒性
对所求问题特征不敏感，对参数设置不敏感，对初始输入数据不敏感
收敛性
错误率
没有被覆盖的解向量与群体规模的比率（error ratio，ER）
n为向量数目
ER为0证明全覆盖
两个解集之间的覆盖率
世代距离
d为与实际的偏离程度
最大出错率
高维空间及其比例
vi是非支配向量，ai是由原点及vi构成的高维空间
H1与H2是测出的与实际的高维空间
基于距离的趋近度评价方法
f为k个目标的最大值和最小值，m为子目标数目
分布性
空间评价方法
基于信息熵的评价方法
影响函数
密度函数
h越大分布性越好
网格分布度评价方法
每个网格的H和h
个体空间分布性评价方法
角坐标
解集分布广度评价指标
综合指标
超体积指标
hypervolume,HV
反转时代距离
inverted generational distance，IGD
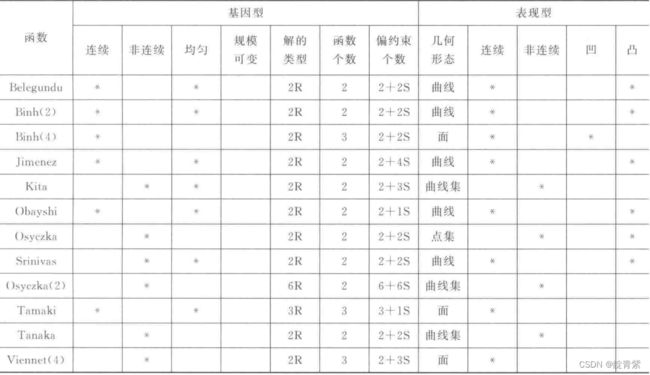
测试函数
基本特征
连续的或非连续的或离散的。
可导的或不可导的。
凸的或凹的。
函数的形态（单峰的，多峰的)。
数值函数或包含字母与数字的函数。
二次方的或非二次方的。
约束条件的类型(等式、不等式、线性的、非线性的)。低维的或高维的（基
因型、表现型)。
欺骗问题或非欺骗问题。
相对PF true有偏好或无偏好。
分类
数值测试函数
带偏约束的
非偏约束
带偏约束的数值
DTLZ
DTLZ1-8
组合优化类
旅行商 着色 顶点覆盖
实验平台
PISA
jMetai
MOEA Framework
OTL
多目标解决单目标
应用
资源配置
地下水质量的监控和处理
土地资源使用规划
供水系统的规划
电力调度
区域服务设施的配置
能源配置
灾后废弃物管理
电子电气
外观与结构优化
VLSL芯片布局
电源分布的最佳布局
电源连接
电磁器件的设计
系统集成
天线的设计
三向感应电机的设计
灯光设计
电路与系统优化设计
dps系统的设计
故障容错系统的设计
CMOS
运算放大器的设计
滤波器的设计
微处理器的设计
组合电路的设计
通信与网络优化方面
无线网络
TCP/IP网络
网络中心通信
机器人方面的应用
机器人路径规划
故障诊断
控制器的设计
机器人手臂操作
航天航空
星座设计
优化控制
航空器的优化设计
空气动力学的优化
市政建设方面
建筑规划
城市规划
交通运输
列车系统
道路系统
运输问题
机械设计与制造
结构设计
生产过程规划与决策
外形设计
机器设计
单元制造
管理工程
噪声管理
突发事件管理
废物最小化管理
生产流程规划
时间表
车间调度
金融方面
投资组合优化
股票排序
经济模型
科学研究
物理
多物理系统设计
3D热感知平面规划
硅太阳能电池优化设计
化学
化学反应过程
危险化学物运输
聚合体挤压优化
生态
生态模型评估
生态装配模型最优
医学
放射性检查
增强放疗
预测模型
三维重建
生物信息学
DNA计算
蛋白质结构预测
计算机科学与工程
主体技术
数据挖掘
机器学习
图像处理
计算机游戏
自动程序设计